Random Variables Continuous and Discrete Probability Distributions Sharif

Random Variables Continuous and Discrete Probability Distributions Sharif University of Technology

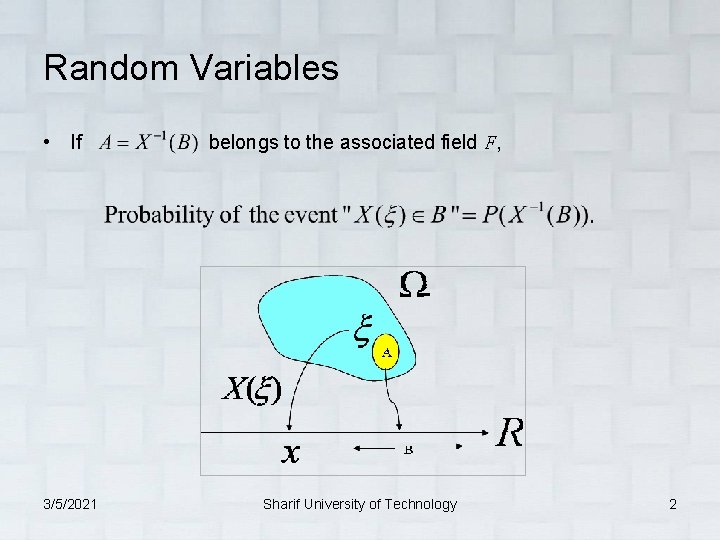
Random Variables • If belongs to the associated field F, 3/5/2021 Sharif University of Technology 2

Random Variable • Definition – If is an event for every x in R, – Random Variable is a finite single valued function that maps the set of all experimental outcomes into the set of real numbers R 3/5/2021 Sharif University of Technology 3

Random Variable • The specification of a random variable can also imply a redefinition of the sample space. Example • we could define as a random variable “the total number of heads. ” • Experiment: Fair coin tossed 3 times, 3/5/2021 Sharif University of Technology 4

Notation • Notation: – RV will always be denoted with uppercase letters – The realized values of the variable (its range) will be denoted by the corresponding lowercase letter. – Thus, the random variable X can take the value x. 3/5/2021 Sharif University of Technology 5

Borel collection • X : r. v, • B represents semi-infinite intervals of the form • The Borel collection B of such subsets of R is the smallest σ-field of subsets of R that includes all semi-infinite intervals of the above form. • if X is a r. v, then is an event for every x. 3/5/2021 Sharif University of Technology 6

Probability Distribution Function(PDF) (Cumulative Distribution Function ) • is said to the Probability Distribution Function associated with the r. v X. • The role of the subscript X is only to identify the actual r. v. 3/5/2021 Sharif University of Technology 7

Properties of a PDF • if g(x) is a distribution function, then – – If then – for all x. 3/5/2021 Sharif University of Technology 8

Properties of a PDF - Proof • The probability distribution function is: – nonnegative – monotone nondecreasing. • Proof - We have: • If then • implies So, 3/5/2021 Sharif University of Technology 9

Properties of a PDF - Proof • Let • Consider the event • Since • We get (mutually exclusive property) • But and hence 3/5/2021 Sharif University of Technology 10

Properties of a PDF - Proof • Thus • But the right limit of x, and hence • i. e. , is right-continuous, justifying all properties of a distribution function. 3/5/2021 Sharif University of Technology 11

Additional Properties • If for some then This follows, since implies is the null set, and for any will be a subset of the null set. • since • The events and are mutually exclusive and their union represents the event 3/5/2021 Sharif University of Technology 12

Additional Properties • Let and • We have: or • Thus the only discontinuities of a distribution function occur at points where 3/5/2021 Sharif University of Technology 13

Example • X is a RV with p. d. f: Find a and P(1< x <2). Example • X is a RV with cdf: a) Compute f(x) and check its properties. b) Find P(− 1 <x<2) using both the pdf and the cdf. 3/5/2021 Sharif University of Technology 14

Continuous-type & Discrete-type R. V • X is said to be a continuous-type r. v if • If is constant except for a finite number of jump discontinuities (piece-wise constant; step-type), then X is said to be a discrete-type r. v. • If is such a discontinuity point, then 3/5/2021 Sharif University of Technology 15

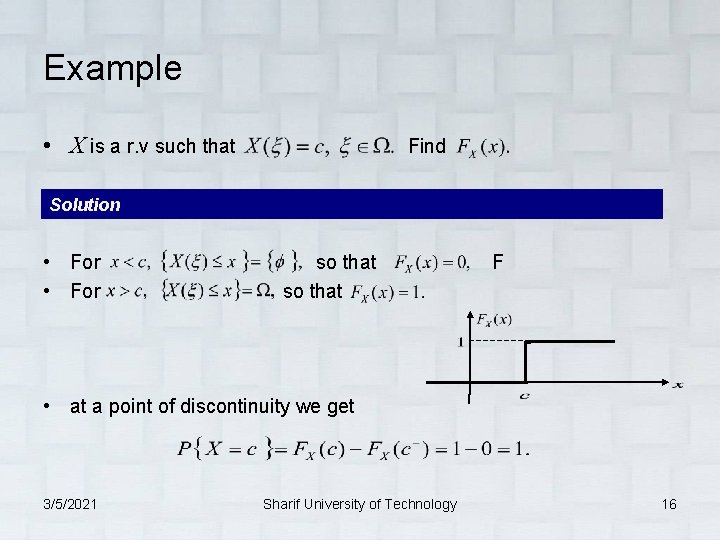
Example • X is a r. v such that Find Solution • For so that F • For so that • at a point of discontinuity we get 3/5/2021 Sharif University of Technology 16

Example • In tossing a coin, Suppose the r. v X is such that Find Solution • For so that • at a point of discontinuity we get 3/5/2021 Sharif University of Technology 17

Example • A fair coin is tossed twice, and let the r. v X represent the number of heads. Find Solution 3/5/2021 Sharif University of Technology 18

Probability Density Function (p. d. f) (Probability Mass Function - for discrete RVs) Since from the monotone-nondecreasing nature of for all x 3/5/2021 Sharif University of Technology 19

Probability Density Function (p. d. f) • X is a continuous type r. v: will be a continuous function • X is a discrete type r. v: has the general form Fig. 3. 5 • represent the jump-discontinuity points in • represents a collection of positive discrete masses, • It is known as the probability mass function (p. m. f ) in the discrete case. 3/5/2021 Sharif University of Technology 20

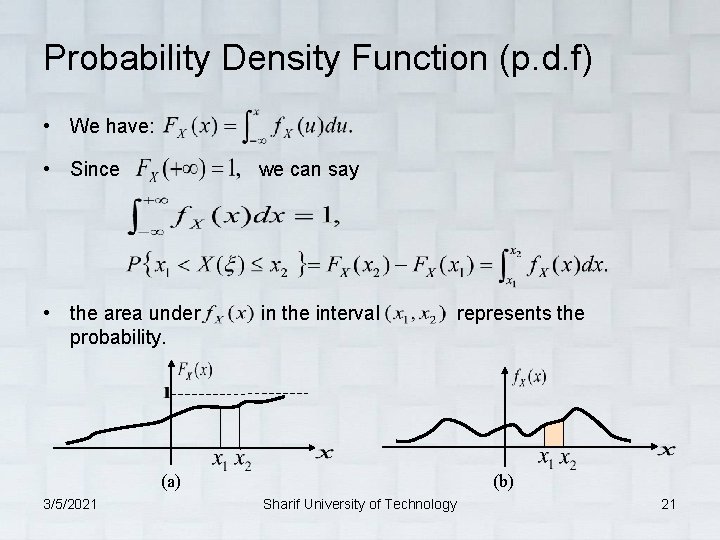
Probability Density Function (p. d. f) • We have: • Since we can say • the area under in the interval represents the probability. (a) 3/5/2021 (b) Sharif University of Technology 21

Continuous-type Random Variables X can take any value in the real line within a bounded or unbounded interval. • • Normal (Gaussian) Uniform Exponential Gamma Beta Chi-Square Rayleigh 3/5/2021 • • Nakagami – m distribution Cauchy Laplace Student’s t-distribution with n degrees of freedom • Fisher’s F-distribution • Others: Weibull, Erlang, Lognormal, … Sharif University of Technology 22

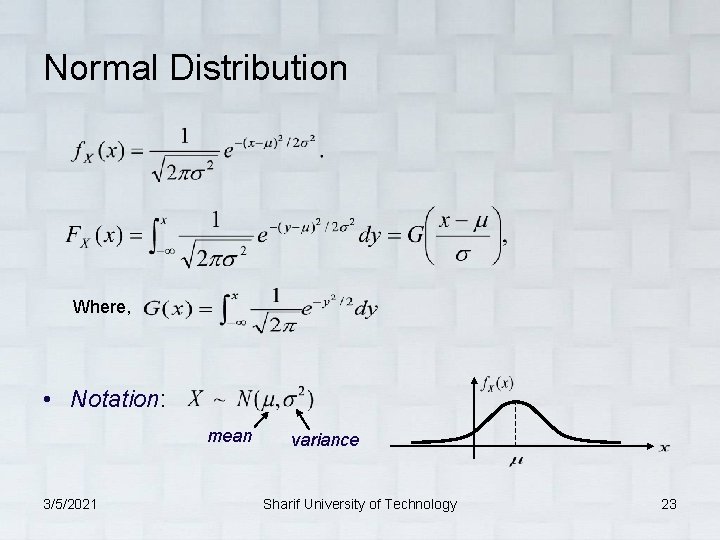
Normal Distribution Where, • Notation: mean 3/5/2021 variance Sharif University of Technology 23

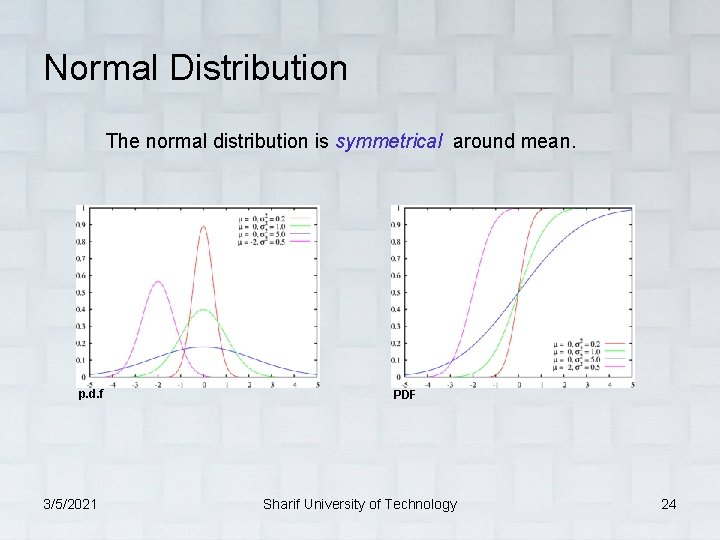
Normal Distribution The normal distribution is symmetrical around mean. p. d. f 3/5/2021 PDF Sharif University of Technology 24

Normal Table • The Normal Distribution illustrated in the table. • With mean of 0 and a standard deviation of 1. • In examples and exercises where z is used, it is found using the formula (x- μ) / σ • or (value given - mean) / standard deviation 3/5/2021 Sharif University of Technology 25

Using the Normal Table • The shaded area, A, gives the probability that Z is greater than the given value. Example • Calculate probability of: – 0 < z < 0. 11 – 0 < z < 0. 34 – 0 < z < 0. 53 3/5/2021 Sharif University of Technology 26

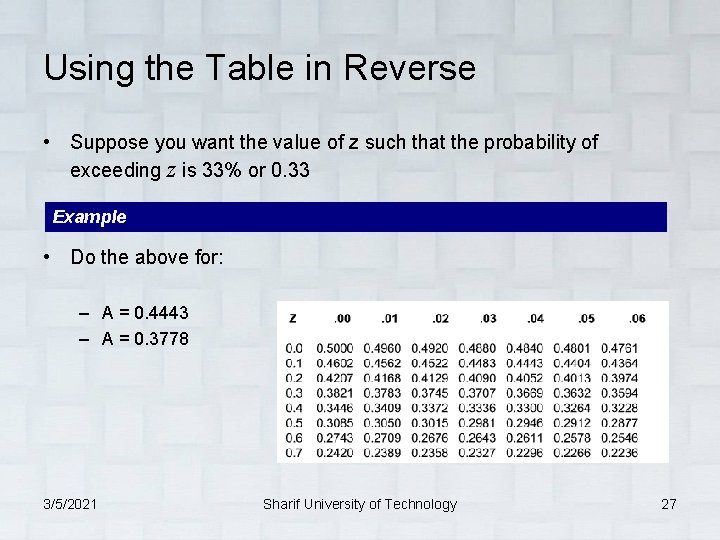
Using the Table in Reverse • Suppose you want the value of z such that the probability of exceeding z is 33% or 0. 33 Example • Do the above for: – A = 0. 4443 – A = 0. 3778 3/5/2021 Sharif University of Technology 27

Applications • Approximately normal distributions occur in many situations. • When a large number of small effects acting additively and independently. • Example: Measurement errors are often assumed to be normally distributed 3/5/2021 Sharif University of Technology 28

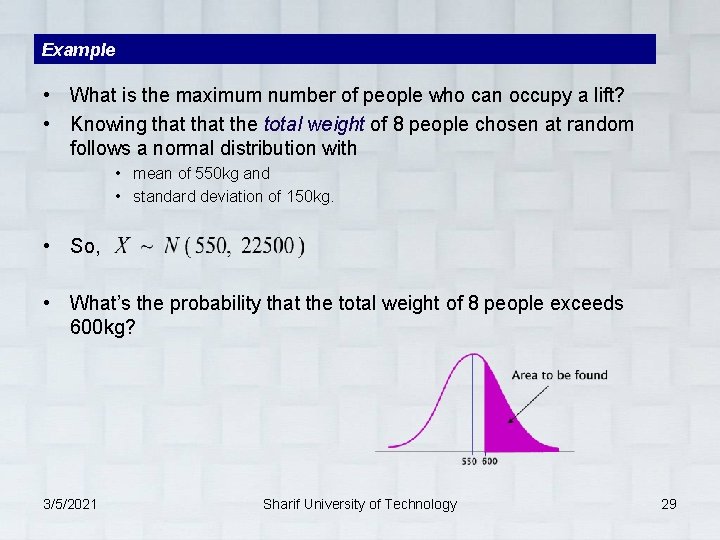
Example • What is the maximum number of people who can occupy a lift? • Knowing that the total weight of 8 people chosen at random follows a normal distribution with • mean of 550 kg and • standard deviation of 150 kg. • So, • What’s the probability that the total weight of 8 people exceeds 600 kg? 3/5/2021 Sharif University of Technology 29

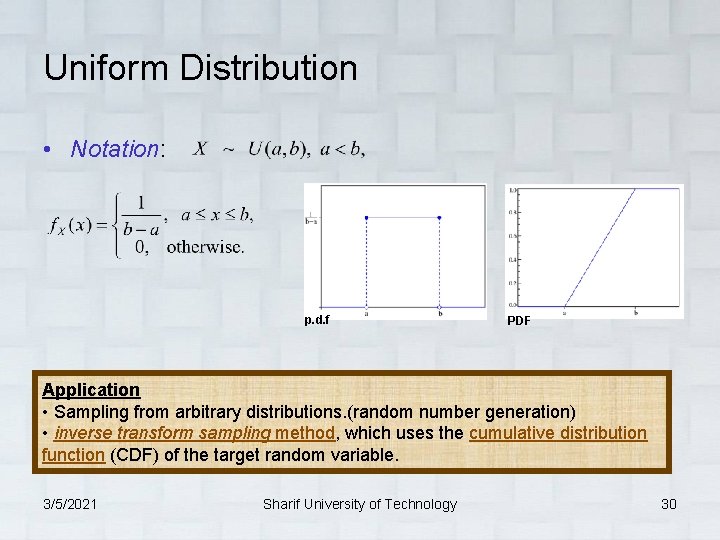
Uniform Distribution • Notation: p. d. f PDF Application • Sampling from arbitrary distributions. (random number generation) • inverse transform sampling method, which uses the cumulative distribution function (CDF) of the target random variable. 3/5/2021 Sharif University of Technology 30

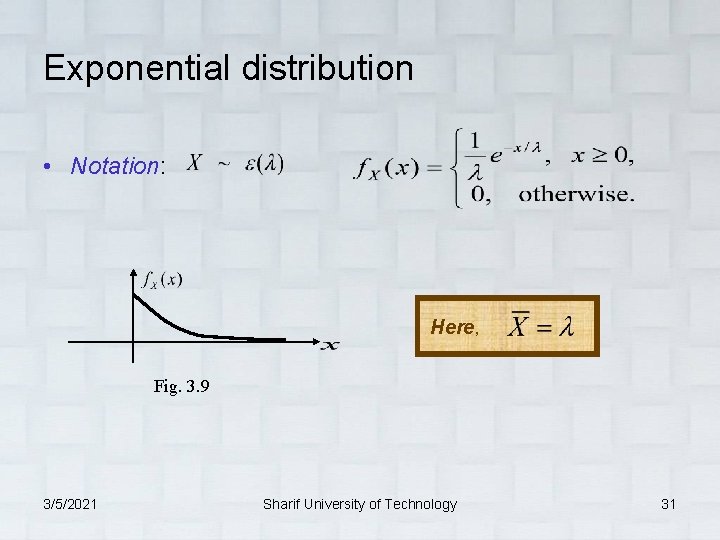
Exponential distribution • Notation: Here, Fig. 3. 9 3/5/2021 Sharif University of Technology 31

Exponential distribution p. d. f 3/5/2021 PDF Sharif University of Technology 32

Exponential Distribution • Assume the occurences of nonoverlapping intervals are independent, and assume: – q(t): the probability that in a time interval t no event has occurred. – x: the waiting time to the first arrival – Then we have: P(x>t)=q(t) – t 1 and t 2 : two consecutive nonoverlapping intervals, 3/5/2021 Sharif University of Technology 33

Exponential Distribution • Then we have: q(t 1) q(t 2) = q(t 1+t 2) • The only bounded solution is: So the pdf is exponential. If the occurrences of events over nonoverlapping intervals are independent, the corresponding pdf has to be exponential. 3/5/2021 Sharif University of Technology 34

Memoryless Property Of Exponential Distribution • Let . Consider the events 3/5/2021 Sharif University of Technology 35

Application • describing the lengths of the inter-arrival times in a homogeneous Poisson processes. – the time it takes before your next telephone call • situations where certain events occur with a constant probability per unit distance: – the distance between mutations on a DNA strand; • Because of memoryless property: – well-suited to model the constant hazard rate in reliability theory. 3/5/2021 Sharif University of Technology 36

Example • Let X denote the time between log-ons to a server in a large corporate network. • Assuming that X has an exponential distribution with minutes, • What is the probability that a log-on occurs within 30 seconds after starting the server? Solution 3/5/2021 Sharif University of Technology 37

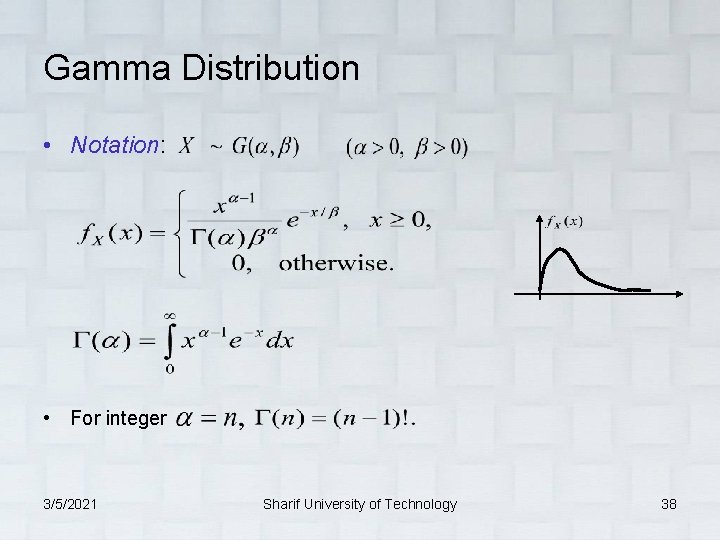
Gamma Distribution • Notation: • For integer 3/5/2021 Sharif University of Technology 38

Gamma Distribution p. d. f 3/5/2021 PDF Sharif University of Technology 39

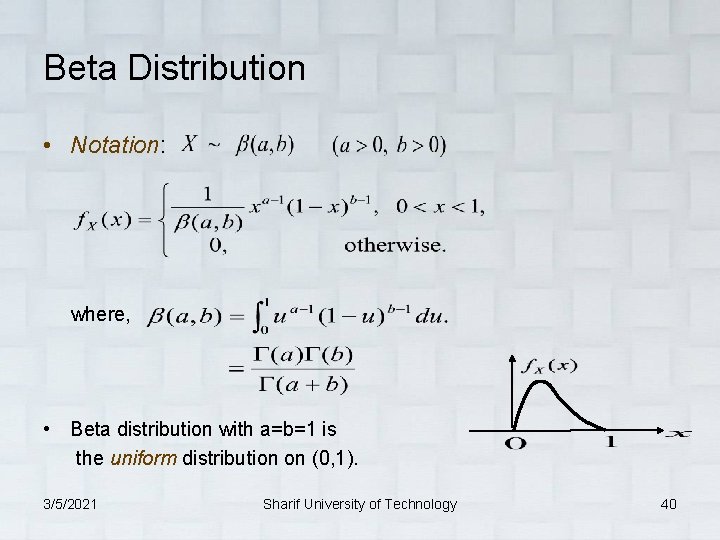
Beta Distribution • Notation: where, • Beta distribution with a=b=1 is the uniform distribution on (0, 1). 3/5/2021 Sharif University of Technology 40

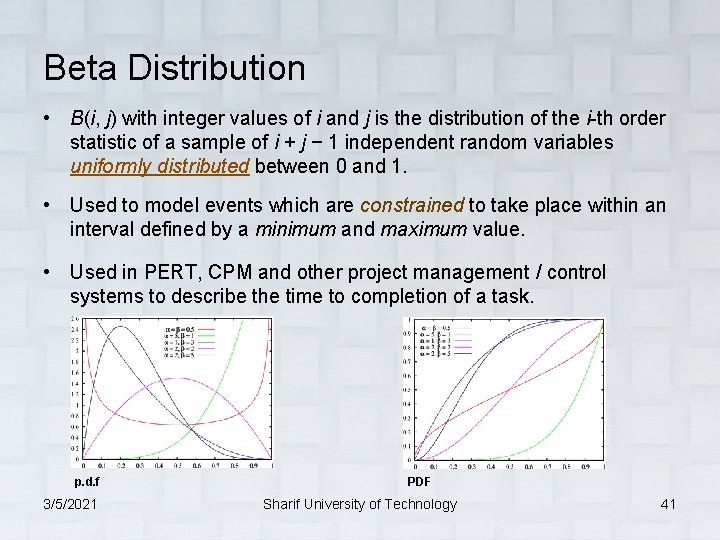
Beta Distribution • B(i, j) with integer values of i and j is the distribution of the i-th order statistic of a sample of i + j − 1 independent random variables uniformly distributed between 0 and 1. • Used to model events which are constrained to take place within an interval defined by a minimum and maximum value. • Used in PERT, CPM and other project management / control systems to describe the time to completion of a task. p. d. f 3/5/2021 PDF Sharif University of Technology 41

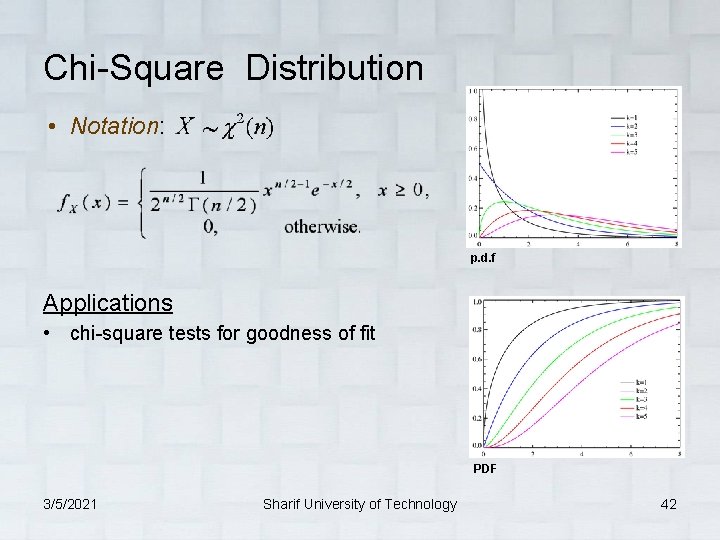
Chi-Square Distribution • Notation: p. d. f Applications • chi-square tests for goodness of fit PDF 3/5/2021 Sharif University of Technology 42

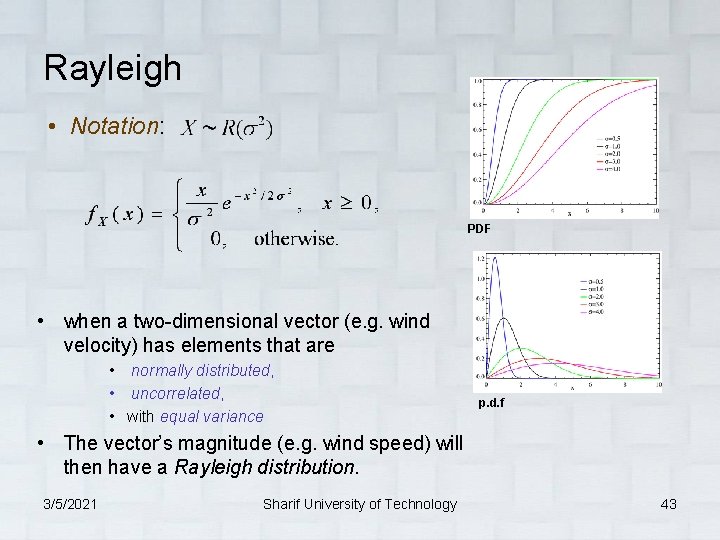
Rayleigh • Notation: PDF • when a two-dimensional vector (e. g. wind velocity) has elements that are • normally distributed, • uncorrelated, • with equal variance p. d. f • The vector’s magnitude (e. g. wind speed) will then have a Rayleigh distribution. 3/5/2021 Sharif University of Technology 43

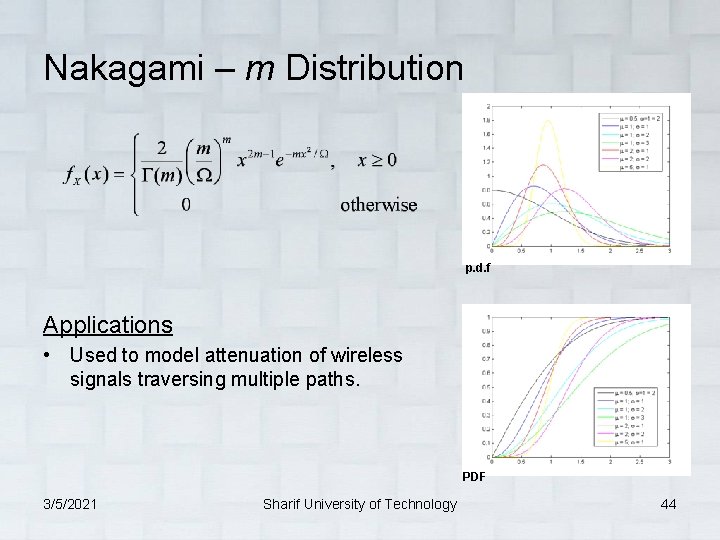
Nakagami – m Distribution p. d. f Applications • Used to model attenuation of wireless signals traversing multiple paths. PDF 3/5/2021 Sharif University of Technology 44

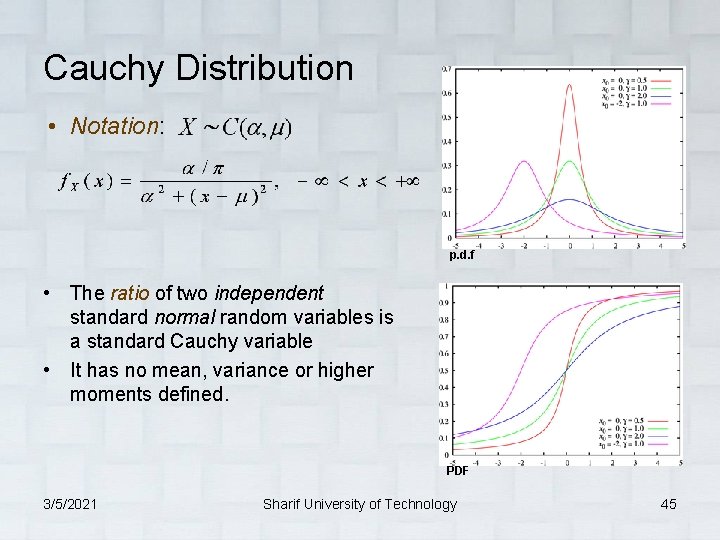
Cauchy Distribution • Notation: p. d. f • The ratio of two independent standard normal random variables is a standard Cauchy variable • It has no mean, variance or higher moments defined. PDF 3/5/2021 Sharif University of Technology 45

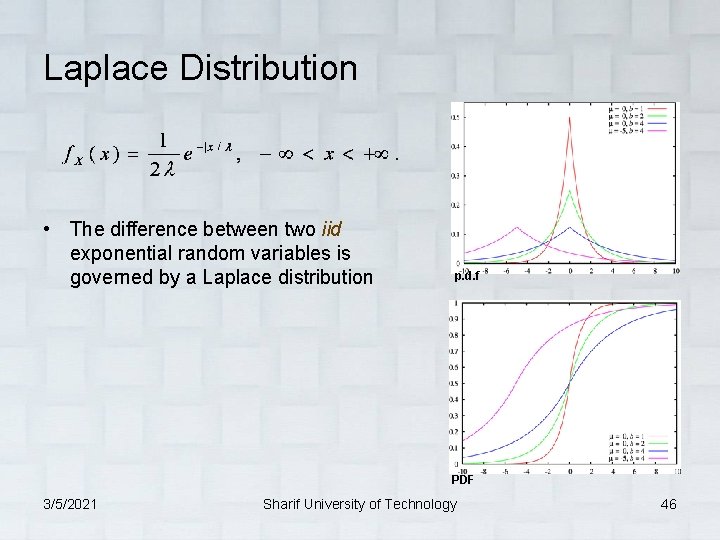
Laplace Distribution • The difference between two iid exponential random variables is governed by a Laplace distribution p. d. f PDF 3/5/2021 Sharif University of Technology 46

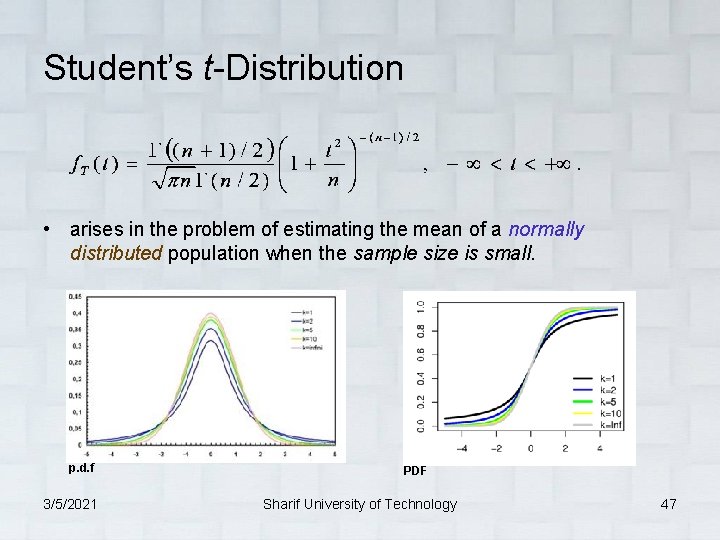
Student’s t-Distribution • arises in the problem of estimating the mean of a normally distributed population when the sample size is small. p. d. f 3/5/2021 PDF Sharif University of Technology 47

Fisher’s F-Distribution • A random variate of the F-distribution arises as the ratio of two chisquared variates p. d. f 3/5/2021 PDF Sharif University of Technology 48

Discrete-type Random Variables X can take only a finite (or countably infinite) number of values • • Bernoulli Binomial Poisson Hypergeometric Geometric Negative Binomial Discrete-Uniform Polya’s distribution 3/5/2021 Sharif University of Technology 49

Bernoulli Distribution X takes the values (0, 1) and, 3/5/2021 Sharif University of Technology 50

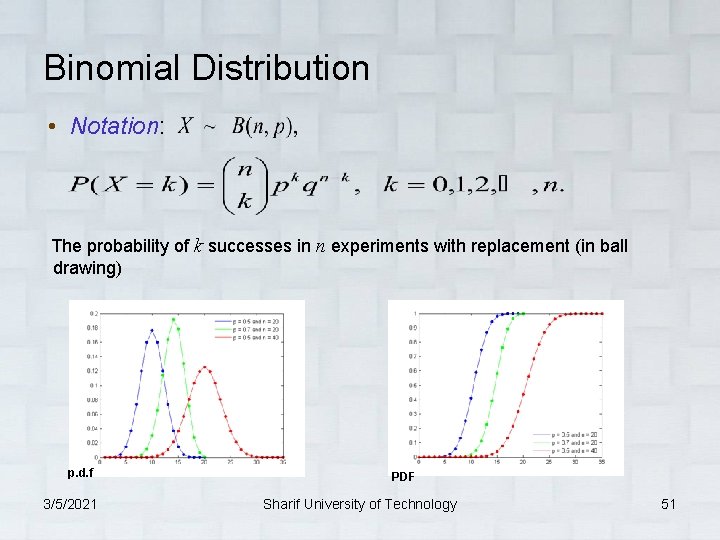
Binomial Distribution • Notation: The probability of k successes in n experiments with replacement (in ball drawing) p. d. f 3/5/2021 PDF Sharif University of Technology 51

Binomial Distribution Example • Assume 5% of a very large population to be green-eyed. • You pick 100 people randomly. • X : The number of green-eyed people • 3/5/2021 Sharif University of Technology 52

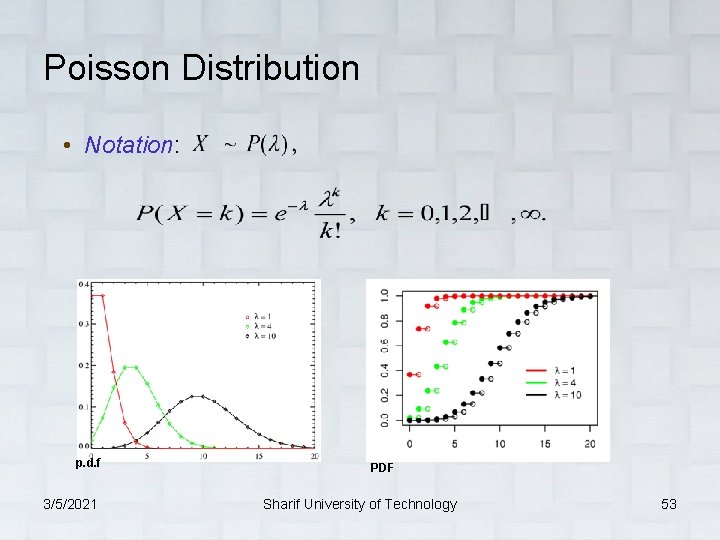
Poisson Distribution • Notation: p. d. f 3/5/2021 PDF Sharif University of Technology 53

Poisson Distribution Law Of Rare Events In a Binomial distribution, as • n approaches ∞ • p approaches 0 • np remains fixed at λ > 0 or at least np approaches λ > 0 The Binomial(n, p) distribution approaches the Poisson distribution with expected value λ. 3/5/2021 Sharif University of Technology 54

Poisson Distribution - Applications • The Poisson distribution applies to various phenomena of discrete nature. • The probability of the phenomenon should be constant in time or space. • Examples: The number of… – spelling mistakes one makes while typing a single page. – phone calls at a call center per minute. – times a web server is accessed per minute. – roadkill (animals killed) found per unit length of road. – pine trees per unit area of mixed forest. – stars in a given volume of space. 3/5/2021 Sharif University of Technology 55

Hypergeometric Distribution • The probability of k successes in n experiments without replacement (ball drawing) Application • The classical application of the hypergeometric distribution is sampling without replacement. 3/5/2021 Sharif University of Technology 56

Geometric Distribution • Notation: the geometric distribution is memoryless. 3/5/2021 Sharif University of Technology 57

Example • From past experience it is known that 3% of accounts in a large accounting population are in error. a) What is the probability that 5 accounts are audited before an account in error is found? b) What is the probability that the first account in error occurs in the first five accounts audited? Solution a) b) 3/5/2021 Sharif University of Technology 58

Negative Binomial Distribution • Notation: • The geometric distribution is a special case of the negative binomial distribution • x independent trials each with two possible outcomes: success/failure. • The probability of success, denoted by p, is the same on every trial. • Continues until r successes are observed 3/5/2021 Sharif University of Technology 59

Example • A basketball player is a 70% free throw shooter. • During the season, what is the probability that he makes his third free throw on his fifth shot? • What is the probability that he makes his first free throw on his fifth shot? 3/5/2021 Sharif University of Technology 60

Discrete-Uniform Distribution Example • In experiment of throwing a die, let X be the random variable denoting what number is thrown. P(X = 1) = 1/6 P(X = 2) = 1/6 etc In fact, P(X = x) = 1/6 for all x between 1 and 6. 3/5/2021 Sharif University of Technology 61

Example: Polya’s distribution Distribution • A box contains a white balls and b black balls. • A ball is drawn at random, and it is replaced along with c balls of the same color. • If X represents the number of white balls drawn in n such draws, find the probability mass function of X. 3/5/2021 Sharif University of Technology 62

Solution : probability of drawing k successive white balls : probability of drawing k white balls , followed by n – k black balls 3/5/2021 Sharif University of Technology 63

Example – cont’d • Polya distribution: probability of getting k white balls in n draws. • if draws are done with replacement, then c = 0 and the above formula simplifies to the binomial distribution 3/5/2021 Sharif University of Technology 64

Example – cont’d • if the draws are conducted without replacement, then c = – 1 and it gives • which represents the hypergeometric distribution. 3/5/2021 Sharif University of Technology 65

Example – cont’d • Finally c = +1 gives (replacements are doubled) • This is Polya’s +1 distribution. 3/5/2021 Sharif University of Technology 66