Random Variables and their Properties Learn fundamental theoretical

Random Variables and their Properties • Learn fundamental theoretical concepts of random variables and probability distributions • Describe the representation of randomness and data variability using probability distributions. • Characterize probability distributions through attributes such as moments (mean, variance, skewness…) and other measures of central tendency. • Estimate parameters of probability distributions from sample data

Text Coverage (Kottegoda and Rosso) • 3. 1 Random Variables, probability distributions and density functions (p 86 -94) • 3. 2 Descriptors of Random Variables – 3. 2. 1 Expectation and other probability measures (p 94103) – 3. 2. 3 Estimation of Parameters by method of moments (p 107 -109), Maximum Likelihood (p 112 -114), Jackknife and Bootstrap (p 116 -117)

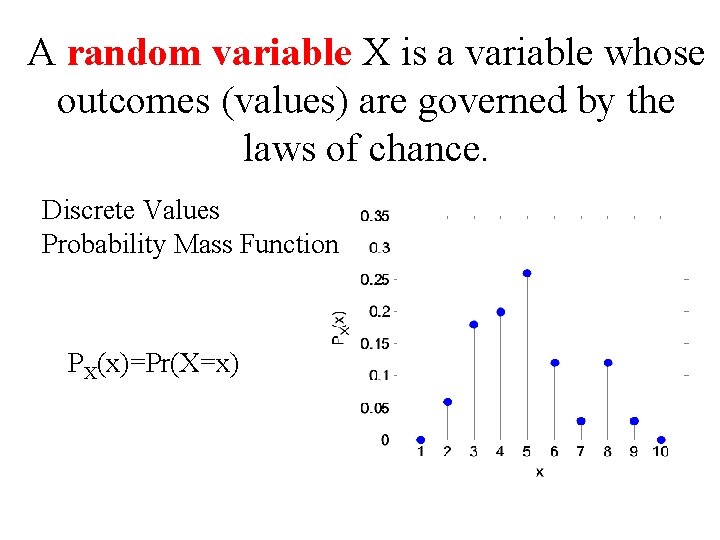
A random variable X is a variable whose outcomes (values) are governed by the laws of chance. Discrete Values Probability Mass Function PX(x)=Pr(X=x)

Cumulative Distribution Function FX(x)=Pr[X ≤ x]

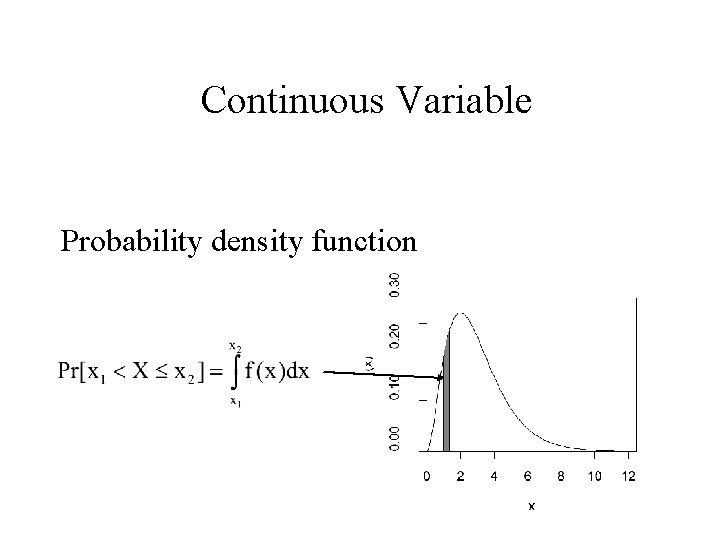
Continuous Variable Probability density function

Cumulative distribution function

Moments of Random Variables

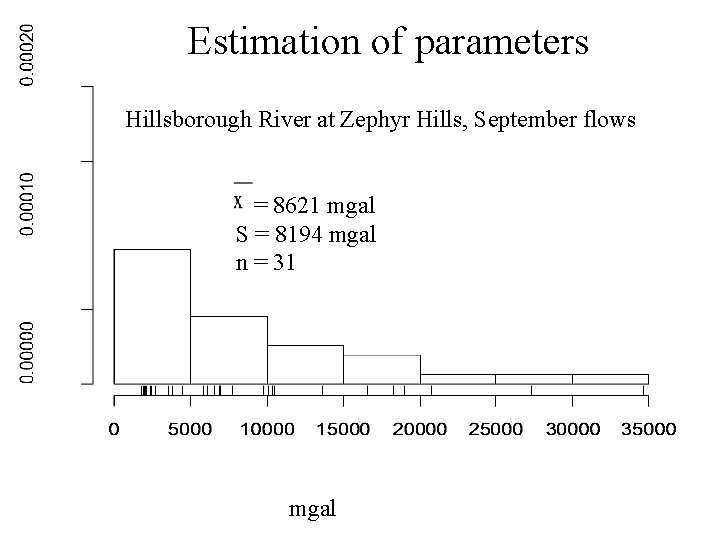
Estimation of parameters Hillsborough River at Zephyr Hills, September flows = 8621 mgal S = 8194 mgal n = 31 mgal

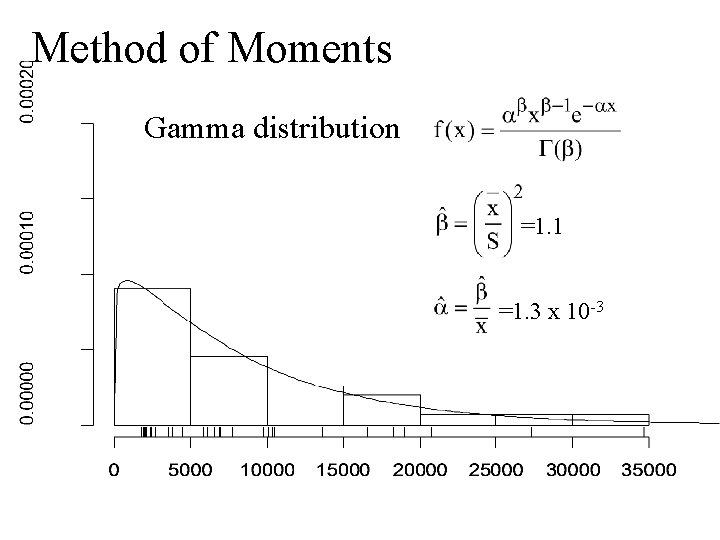
Method of Moments Gamma distribution =1. 1 =1. 3 x 10 -3

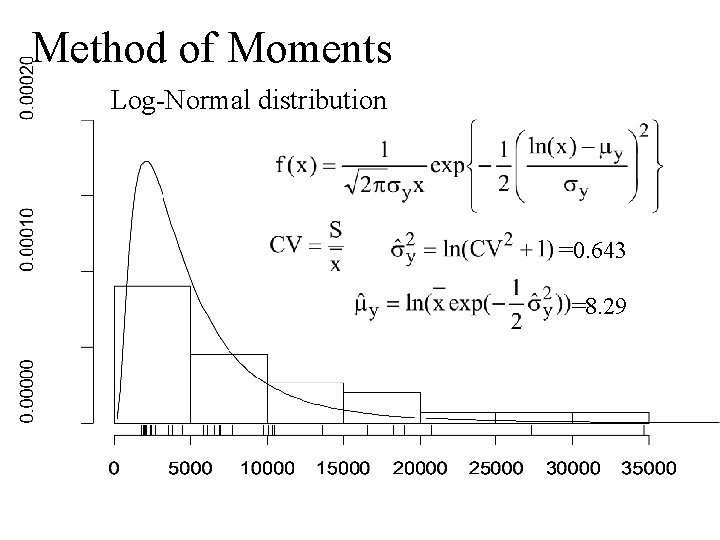
Method of Moments Log-Normal distribution =0. 643 =8. 29

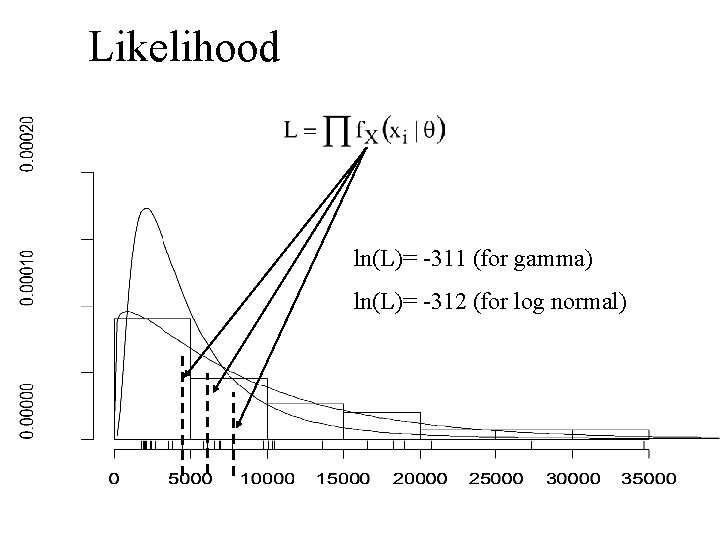
Likelihood ln(L)= -311 (for gamma) ln(L)= -312 (for log normal)

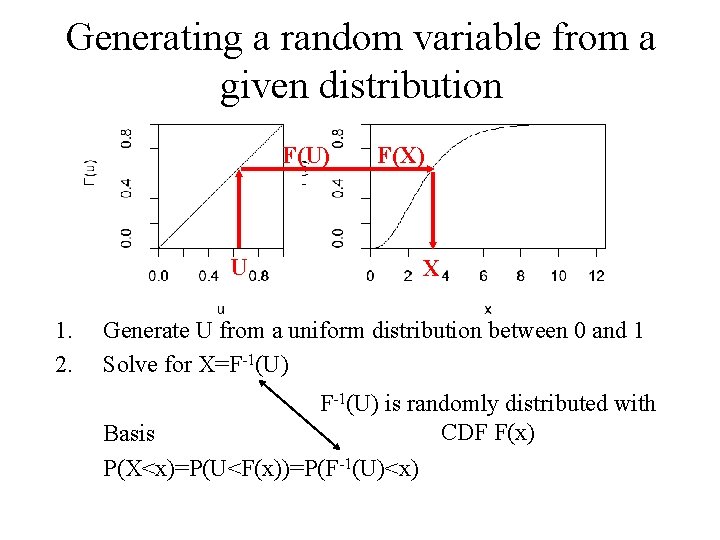
Generating a random variable from a given distribution F(U) F(X) U 1. 2. X Generate U from a uniform distribution between 0 and 1 Solve for X=F-1(U) is randomly distributed with CDF F(x) Basis P(X<x)=P(U<F(x))=P(F-1(U)<x)

Generating a Pseudo random number • There is a lot of lore about this. Refer to: Press, W. H. , B. P. Flannery, S. A. Teukolsky and W. T. Vetterling, (1988), Numerical Recipes in C : The Art of Scientific Computing, Cambridge University Press, New York, 735 p. • Congruential method • Each r is an integer random number between 0 and m-1. by (m-1) gives a number between 0 and 1 that repeats after at most m numbers. Numerical recipes gives "good" choices for a, c and m. • R has built in functions runif to generate uniform random numbers, as well as other distributions, e. g rnorm, rgamma.

Generating a random variable from a discrete distribution in matlab F(U) F(X) U Xs=[x 1 x 2 x 3 …] Px=[p 1 p 2 p 3 …] CDFx=cumsum(Px) U=rand(1) X = Xs(find(CDFx>U, 1) ) X % % % Vector of x values Vector of pmf values CDF vector Uniform random number 0 -1 Inverse of CDF