Random Variables and Probability Distributions l A random

Random Variables and Probability Distributions l A random variable is a function or rule that assigns a numerical value to each simple event in a sample space. l 為了降低分析的複雜性,將所有可能結果加以數值化 例如投銅板十次,正面出現次數的事件就是random variable l 短期不知道是什麼,長期下來會呈現某種分配 l l There are two types of random variables: l l 2 Discrete random variable Continuous random variable Jia-Ying Chen

Discrete Probability Distribution l A table, formula, or graph that lists all possible values a discrete random variable can assume, together with associated probabilities, is called a discrete probability distribution. l To calculate the probability that the random variable X assumes the value x, P(X = x), l l l 3 add the probabilities of all the simple events for which X is equal to x, or Use probability calculation tools (tree diagram), Apply probability definitions Jia-Ying Chen

Example 1 l l The number of cars a dealer is selling daily were recorded in the last 100 days. This data was summarized in the table below. Estimate the probability distribution, and determine the probability of selling more than 2 cars a day. Daily sales Frequency 0 5 1 15 2 35 3 25 4 20 100 4 Jia-Ying Chen

Solution l From the table of frequencies we can calculate the relative frequencies, which becomes our estimated probability distribution Daily sales Relative Frequency 0 5/100=. 05 1 15/100=. 15 2 35/100=. 35 3 25/100=. 25 4 20/100=. 20 1. 00 5 . 35. 25. 15 . 20 . 05 0 1 2 P(X>2) = P(X=3) + P(X=4) =. 25 +. 20 =. 45 3 X 4 Jia-Ying Chen

Describing the Population/ Probability Distribution l l l 6 The probability distribution represents a population We’re interested in describing the population by computing various parameters. Specifically, we calculate the population mean and population variance. Jia-Ying Chen

Population Mean (Expected Value) and Population Variance l Given a discrete random variable X with values xi, that occur with probabilities p(xi), the population mean of X is. l l 加權平均概念(權數是機率) Let X be a discrete random variable with possible values xi that occur with probabilities p(xi), and let E(xi) = m. The variance of X is defined by V(X) = s 2 = E[(X - m)2 ]= å (xi - m)2 p(xi ) all xi 7 Jia-Ying Chen

The Mean and the Variance 8 l The variance can also be calculated as follows: l Proof Jia-Ying Chen

Laws of Expected Value and Variance l Laws of Expected Value § § § l Laws of Variance § § § 9 E(c) = c E(X + c) = E(X) + c E(c. X) = c. E(X) V(c) = 0 V(X + c) = V(X) V(c. X) = c 2 V(X) Jia-Ying Chen

Example 2 l We are given the following probability distribution: x 0 P(x) 0. 4 l l 10 1 2 3 0. 2 0. 1 a. Calculate the mean, variance, and standard deviation b. Suppose that Y=3 X+2. For each value of X, determine the value of Y. What is the probability distribution of Y? c. Calculate the mean, variance, and standard deviation from the probability distribution of Y. d. Use the laws of expected value and variance to calculate the mean, variance, and standard deviation of Y from the mean, variance, and standard deviation of X. Compare your answers in Parts c and d. Are they the same (except for rounding) Jia-Ying Chen

Solution l a. E(X) = 0(0. 4) +1(0. 3) + 2(0. 2) +3(0. 1) = 1 V(X)=E(X 2)-{E(X)}2 l l =(0)2(0. 4)+(1)2(0. 3)+(2)2(0. 2)+(3)2(0. 1)-(1)2 =1 l l b. x y P(y) 11 0 2 0. 4 1 5 0. 3 2 8 0. 2 3 11 0. 1 Jia-Ying Chen

Solution l c. l l E(Y) = 2(0. 4) + 5(0. 3) + 8(0. 2) + 11(0. 1) = 5 V(Y)=E(Y 2)-{E(Y)}2 =(2)2(0. 4)+(5)2(0. 3)+(8)2(0. 2)+(11)2(0. 1)-(5)2 =9 l l d. l l 12 E(Y) = E(3 X+2) = 3 E(X)+2 = 5 V(Y) = V(3 X+2) = 9 V(X) = 9 Jia-Ying Chen

Bivariate Distributions l The bivariate (or joint) distribution is used when the relationship between two random variables is studied. l l 13 也就是第六章所看到的聯合機率分配 The probability that X assumes the value x, and Y assumes the value y is denoted p(x, y) = P(X=x and Y = y) Jia-Ying Chen

Bivariate Distributions l 14 Example 7. 5 l Xavier and Yvette are two real estate agents. Let X and Y denote the number of houses that Xavier and Yvette will sell next week, respectively. l The bivariate probability distribution is presented next. Jia-Ying Chen
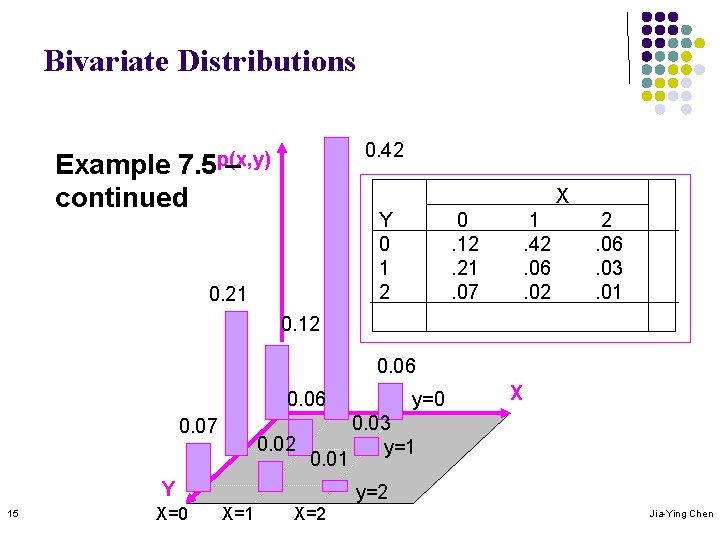
Bivariate Distributions 0. 42 7. 5 p(x, y) – Example continued X Y 0 1 2 0. 21 0. 12. 21. 07 1. 42. 06. 02 2. 06. 03. 01 0. 12 0. 06 0. 07 0. 02 0. 01 Y 15 X=0 y=0 X 0. 03 y=1 y=2 X=1 X=2 Jia-Ying Chen

Marginal Probabilities l Example 7. 5 – continued l Sum across rows and down columns X p(0, 0) p(0, 1) p(0, 2) 16 Y 0 1 2 p(x) 0. 12. 21. 07. 40 1. 42. 06. 02. 50 The marginal probability P(X=0) 2. 06. 03. 01. 10 p(y). 60. 30. 10 1. 00 P(Y=1), the marginal probability. Jia-Ying Chen

Describing the Bivariate Distribution l l The joint distribution can be described by the mean, variance, and standard deviation of each variable. This is done using the marginal distributions. x p(x) y p(y) 0. 6 1. 3 2 2 17 . 4 0 . 5 1 . 1. 1 E(X) =. 7. 5 E(Y) = Jia-Ying Chen

Describing the Bivariate Distribution l To describe the relationship between the two variables we compute the covariance and the coefficient of correlation l Covariance: l l Coefficient of Correlation l 18 COV(X, Y) = S(X – mx)(Y- my)p(x, y)=E(XY)-E(X)E(Y) COV(X, Y) sxsy Jia-Ying Chen

Describing the Bivariate Distribution l Example 7. 6 l l Calculate the covariance and coefficient of correlation between the number of houses sold by the two agents in Example 7. 5 Solution = S(x-mx)(y-my)p(x, y) = (0 -. 7)(0 -. 5)p(0, 0)+…(2 -. 7)(2 -. 5)p(2, 2) = -. 15 l r=COV(X, Y)/sxsy = -. 15/(. 64)(. 67) = -. 35 l COV(X, Y) X Y 0 1 2 p(x) 19 0. 12. 21. 07. 40 1. 42. 06. 02. 50 2. 06. 03. 01. 10 p(y). 60. 30. 10 1. 00 Jia-Ying Chen

Sum of Two Variables l The probability distribution of X + Y is determined by l l l Example 7. 5 - continued l l 20 Determining all the possible values that X+Y can assume For every possible value C of X+Y, adding the probabilities of all the combinations of X and Y for which X+Y = C Find the probability distribution of the total number of houses sold per week by Xavier and Yvette. Solution l X+Y is the total number of houses sold. X+Y can have the values 0, 1, 2, 3, 4. Jia-Ying Chen

The Probability Distribution of X+Y P(X+Y=0) = P(X=0 and Y=0) =. 12 P(X+Y=1) = P(X=0 and Y=1)+ P(X=1 and Y=0) =. 21 +. 42 =. 63 P(X+Y=2) = P(X=0 and Y=2)+ P(X=1 and Y=1)+ P(X=2 and Y =. 07 +. 06 =. 19 X 21 Y 0 1 2 p(y) 0. 12. 42. 06. 60 1. 21. 06. 03. 30 2. 07. 02. 01. 10 p(x). 40. 50. 10 1. 00 The probabilities P(X+Y)=3 and P(X+Y) =4 are calculated the same way. The distribution follows Jia-Ying Chen

The Expected Value and Variance of X+Y l The distribution of X+Y x+y p(x+y) l 2. 19 3. 05 4. 01 The expected value and variance of X+Y can be calculated from the distribution of X+Y. l l 22 0 1. 12. 63 E(X+Y)=0(. 12)+ 1(63)+2(. 19)+3(. 05)+4(. 01)=1. 2 V(X+Y)=(0 -1. 2)2(. 12)+(1 -1. 2)2(. 63)+… =. 56 Jia-Ying Chen

The Expected Value and Variance of X+Y l The following relationship can assist in calculating E(X+Y) and V(X+Y) E(X+Y) =E(X) + E(Y); l V(X+Y) = V(X) +V(Y) +2 COV(X, Y) l When X and Y are independent COV(X, Y) = 0, and V(X+Y) = V(X)+V(Y). l Proof l 23 Jia-Ying Chen

Example 3 l The bivariate distribution of X and Y is described here. x l l l 24 y 1 2 1 0. 28 0. 42 2 0. 18 a. Find the marginal probability distribution of X. b. Find the marginal probability distribution of Y c. Compute the mean and variance of X d. Compute the mean and variance of Y e. Compute the covariance and variance of Y Jia-Ying Chen

Solution l l l 25 a x P(x) 1. 4 2. 6 b y P(y) 1. 7 2. 3 c E(X) = 1(. 4) + 2(. 6) = 1. 6 V(X) = (1– 1. 6)^2*(. 4) + (2– 1. 6)^2*(. 6) =. 24 or (1^2)*0. 4+(2^2)*0. 6 -(1. 6)^2=. 24 Jia-Ying Chen

Solution l l 26 d E(Y) = 1(. 7) + 2(. 3) = 1. 3 V(Y) = (1– 1. 3)^2(. 7) + (2– 1. 3)^2(. 3) =. 21 e E(XY) = (1)(1)(. 28) + (1)(2)(. 12) + (2)(1)(. 42) + (2)(2)(. 18) = 2. 08 COV(X, Y) = E(XY)–E(X)E(Y) = 2. 08 – (1. 6)(1. 3) = 0 =0 Jia-Ying Chen

The Binomial Distribution l l The binomial experiment can result in only one of two possible outcomes. Binomial Experiment l l l Binomial Random Variable l l 27 There are n trials (n is finite and fixed). Each trial can result in a success or a failure. The probability p of success is the same for all the trials. All the trials of the experiment are independent The binomial random variable counts the number of successes in n trials of the binomial experiment. By definition, this is a discrete random variable. Jia-Ying Chen

Calculating the Binomial Probability In general, The binomial probability is calculate Mean and Variance of Binomial Variable 28 Jia-Ying Chen

Example 4 l a. b. 29 In the game of blackjack as played in casinos in Las Vegas, Atlantic City, Niagara Falls, as well as many other cities, the dealer has the advantages. Most players do not play very well. As a result, the probability that the average player wins a about 45%. Find the probability that an average player wins twice in 5 hands ten or more times in 25 hands Jia-Ying Chen

Solution 30 l a P(X = 2) = =. 3369 l b Excel with n = 25 and p =. 45: P(X 10) = 1 – P(X 9) = 1 –. 2424 =. 7576 Jia-Ying Chen

Poisson Distribution 31 l The Poisson experiment typically fits cases of rare events that occur over a fixed amount of time or within a specified region l Typical cases l The number of errors a typist makes per page l The number of customers entering a service station per hour l The number of telephone calls received by a switchboard per hour. Jia-Ying Chen

Properties of the Poisson Experiment l The number of successes (events) that occur in a certain time interval is independent of the number of successes that occur in another time interval. l The probability of a success in a certain time interval is l the same for all time intervals of the same size, l proportional to the length of the interval. The probability that two or more successes will occur in an interval approaches zero as the interval becomes smaller. l 32 Jia-Ying Chen

The Poisson Variable and Distribution 33 l The Poisson Random Variable l The Poisson variable indicates the number of successes that occur during a given time interval or in a specific region in a Poisson experiment l Probability Distribution of the Poisson Random Variable. Jia-Ying Chen

Example 5 l a. b. 34 The number of students who seek assistance with their statistics assignments is Poisson distributed with a mean of three per day. What is the probability that no student seek assistance tomorrow? Find the probability that 10 students seek assistance in a week. Jia-Ying Chen

Solution 35 l a. P(X = 0 with = 3) = = =. 0498 l b. P(X = 10 with = 21) = = =. 0035 Jia-Ying Chen

Continuous Probability Distributions l A continuous random variable has an uncountably infinite number of values in the interval (a, b). l The probability that a continuous variable X will assume any particular value is zero. Why? 1/4 1/3 1/2 0 36 The probability of each value + 1/4 + + 1/3 1/2 2/3 1/4 = 1 1/3 = 1 1/2 = 1 1 Jia-Ying Chen

Continuous Probability Distributions As the number of values increases the probability of each value decreases. This is so because the sum of all the probabilities remains 1. When the number of values approaches infinity (because X is continuous) the probability of each value approaches 0. 1/4 1/3 1/2 0 37 The probability of each value + 1/4 + + 1/3 1/2 2/3 1/4 = 1 1/3 = 1 1/2 = 1 1 Jia-Ying Chen

Probability Density Function l l To calculate probabilities we define a probability density function f(x). The density function satisfies the following conditions l l Area = 1 f(x) is non-negative, P(x 1<=X<=x 2) The total area under the curve representing f(x) equals 1. x 1 x 2 • The probability that X falls between x 1 and x 2 is found by calculating the area under the graph of f(x) between x 1 and x 2. 38 Jia-Ying Chen

Uniform Distribution 39 l A random variable X is said to be uniformly distributed if its density function is l The expected value and the variance are Jia-Ying Chen

Example 6 l a. b. 40 The weekly output of a steel mill is a uniformly distributed random variable that lies between 110 and 175 metric tons. Compute the probability that the steel mill will produce more than 150 metric tons next week. Deter the probability that the steel mill will produce between 120 and 160 metric tons next week. Jia-Ying Chen

Solution 41 , 110 ≦ x ≦ 175 l f(x) = l a P(X ≧ 150) = l b P(120 ≦ X ≦ 160) = = 0. 3846 = 0. 6154 Jia-Ying Chen
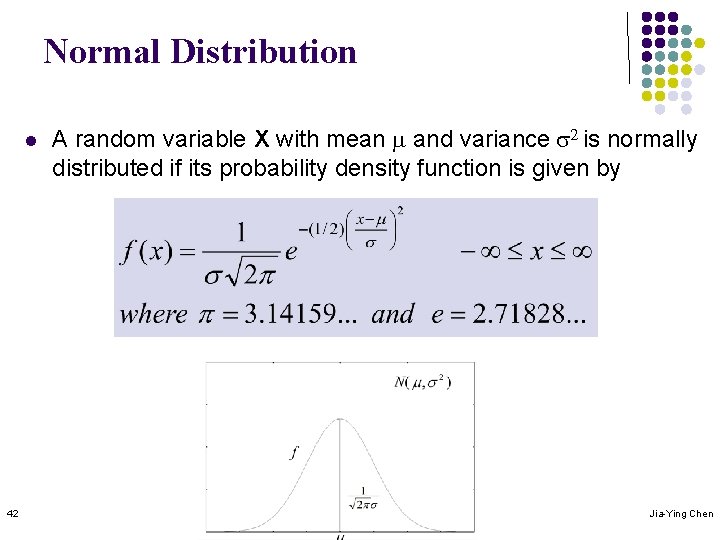
Normal Distribution l 42 A random variable X with mean m and variance s 2 is normally distributed if its probability density function is given by Jia-Ying Chen

Finding Normal Probabilities l Two facts help calculate normal probabilities: l l l “Standard Normal Distribution” l Example: l 43 The normal distribution is symmetrical. Any normal distribution can be transformed into a specific normal distribution called… The amount of time it takes to assemble a computer is normally distributed, with a mean of 50 minutes and a standard deviation of 10 minutes. What is the probability that a computer is assembled in a time between 45 and 60 minutes? Jia-Ying Chen

Finding Normal Probabilities l Solution l l If X denotes the assembly time of a computer, we seek the probability P(45 ≦ X ≦ 60). This probability can be calculated by creating a new normal variable the standard normal variable. Every normal variable with some m and s, can be transformed into this Z. 44 E(Z) = m = 0 Therefore, once probabilities fo are calculated, probabilities of normal variable can be found. V(Z) = s 2 = 1 Jia-Ying Chen

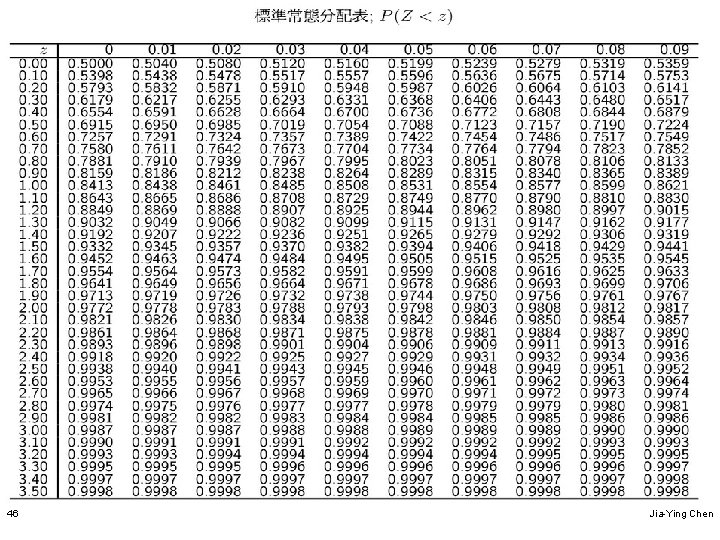
Finding Normal Probabilities l Example - continued 45 - 50 P(45 ≦ X ≦ 60) = P( 10 X- m ≦ s 60 - 50 ≦ 10 ) = P(-0. 5 ≦ Z ≦ 1) To complete the calculation we need to compu the probability under the standard normal distr 45 Jia-Ying Chen
46 Jia-Ying Chen
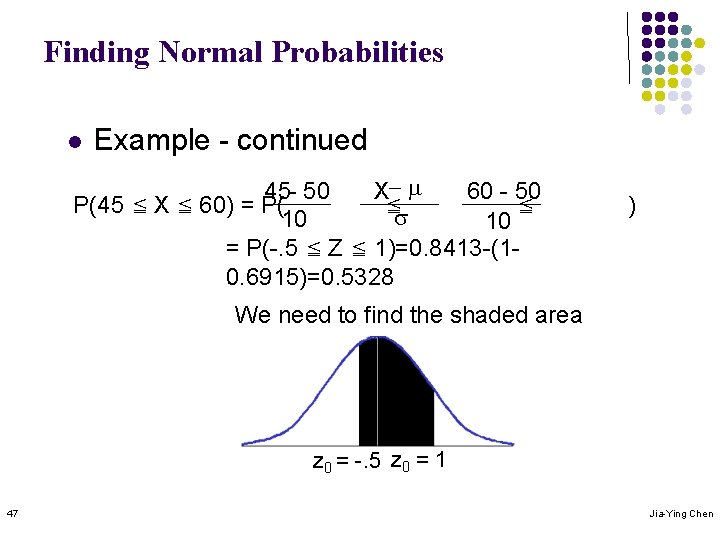
Finding Normal Probabilities l Example - continued 45 - 50 X- m 60 - 50 P(45 ≦ X ≦ 60) = P( ≦ ≦ s 10 10 = P(-. 5 ≦ Z ≦ 1)=0. 8413 -(10. 6915)=0. 5328 ) We need to find the shaded area z 0 = -. 5 z 0 = 1 47 Jia-Ying Chen

Example 7 l l l 48 X is normally distributed with mean 300 and standard deviation 40. What value of X does only the top 15 % exceed? P(0 < Z < = 1. 04; ) = 1 -0. 15 = 0. 85 Jia-Ying Chen

Example 8 l l 49 The long-distance calls made by the employees of a company are normally distributed with a mean of 7. 2 minutes and a standard deviation of 1. 9 minutes. Find the probability that a call a. Last between 5 and 10 minutes b. Last more than 7 minutes c. Last less than 4 minutes Jia-Ying Chen

Solution 50 l a P(5 < X < 10) = = P(– 1. 16 < Z < 1. 47) = 0. 9292 -(1 -0. 8770) =. 8062 l b. P(X > 7) = l c. P(X < 4) = =1 -0. 9535=. 0465 = P(Z > –. 11) = 0. 5438 Jia-Ying Chen
- Slides: 50