Random Variable PMF Probability Mass Function Expected Value

Random Variable, PMF (Probability Mass Function), Expected Value, Variance STAT 400.

Variable : a characteristic that varies from one subject to another Ex: height, weight, mpg, gender, eye color, favorite sports Quantitative variable (Numerical variable) Qualitative variable (Categorical Variable)

Random Variable (RV)

Random Variable (RV) Discrete random variable: ◦ Countable # of values in S Continuous random variable: ◦ Uncountable # of values in S ◦ Can take on any values in a range

Two fair coin toss (example) A balanced (fair) coin is tossed twice. Let X denote the number of Heads. S: {HH, HT, TH, TT} Outcomes x TT 0 HT, TH 1 HH 2

Probability Mass Function (PMF) Summarizes the probabilities for a discrete random variable by a probability assignment for each distinct value by a function. Support: the set of values that the Random Variable can have

Probability Mass Function (PMF)

Probability Mass Function (PMF)

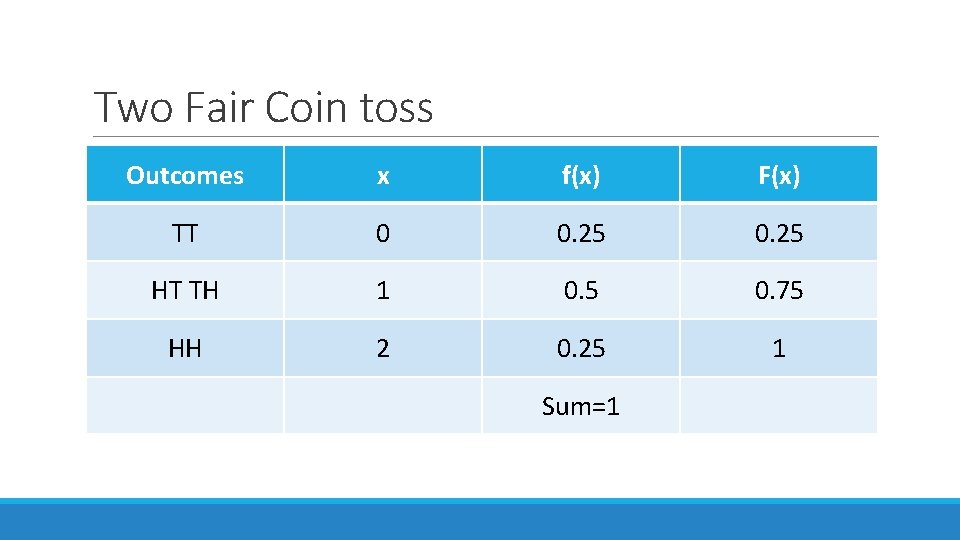
Two Fair Coin toss Outcomes x f(x) F(x) TT 0 0. 25 HT TH 1 0. 5 0. 75 HH 2 0. 25 1 Sum=1

Example x f(x) 0 0. 1 1 0. 2 2 0. 3 3 0. 3 4

Expected value of discrete RV

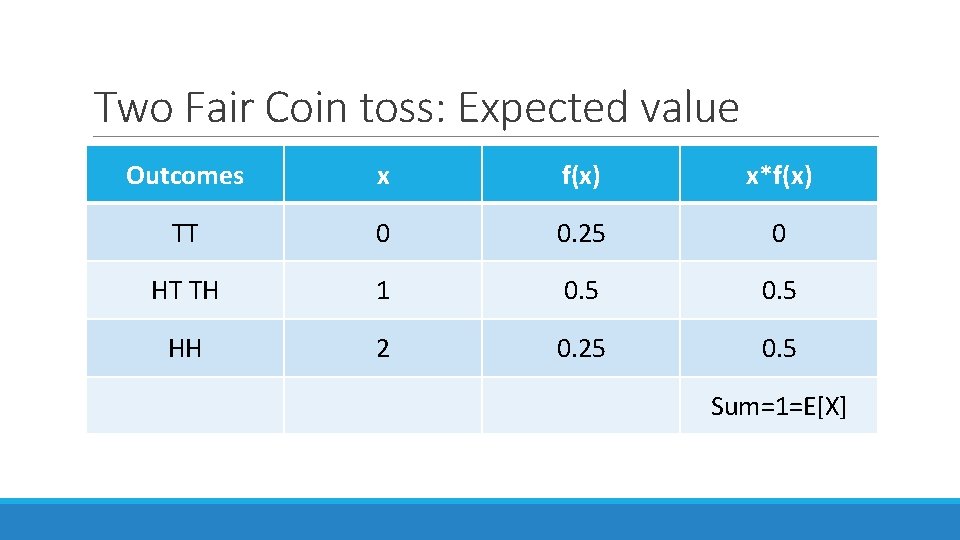
Two Fair Coin toss: Expected value Outcomes x f(x) x*f(x) TT 0 0. 25 0 HT TH 1 0. 5 HH 2 0. 25 0. 5 Sum=1=E[X]

Properties of Expected Value

Variance of discrete RV

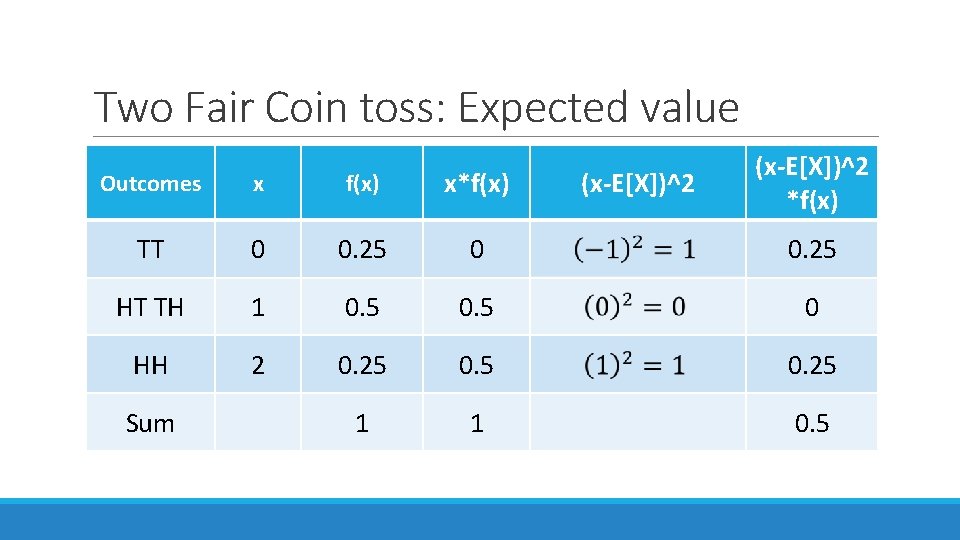
Two Fair Coin toss: Expected value Outcomes x f(x) x*f(x) TT 0 0. 25 HT TH 1 0. 5 0 HH 2 0. 25 1 1 0. 5 Sum (x-E[X])^2 *f(x)

Properties of Variance

Example Homer Simpson is going to Moe’s Tavern for some Flaming Moe’s. Let X denote the number of Flaming Moe’s that Homer Simpson will drink. Suppose X has the following probability distribution: x f(x) 0 0. 1 1 0. 2 2 0. 3 3 0. 3 4 d) Compute the expected value of X, E ( X ). (A) 1. 0 (B) 2. 0 (C) 2. 1 (D) 2. 3 e) Compute the standard deviation of X, SD ( X ). (A) 5. 7 (B) 2. 3875 (C) 1. 29 (D) 1. 1358

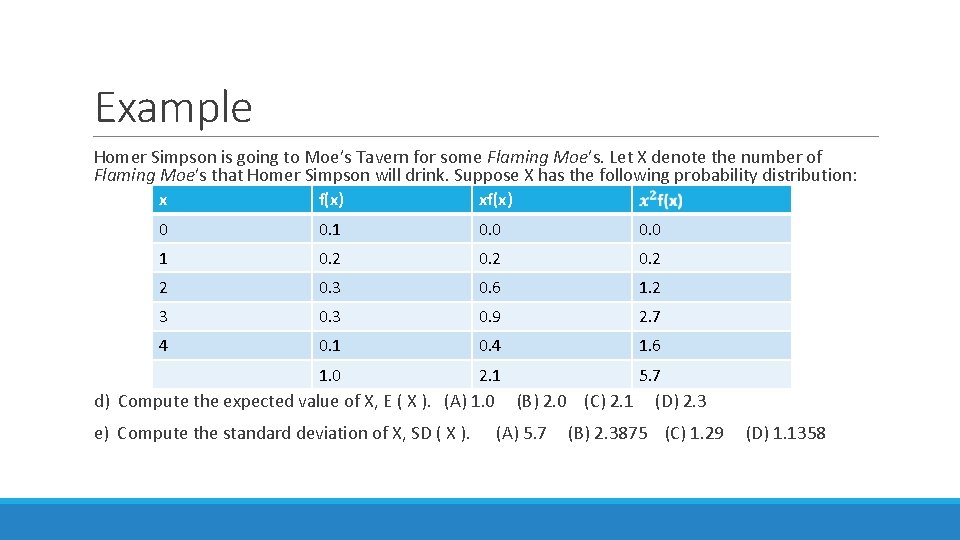
Example Homer Simpson is going to Moe’s Tavern for some Flaming Moe’s. Let X denote the number of Flaming Moe’s that Homer Simpson will drink. Suppose X has the following probability distribution: x f(x) xf(x) 0 0. 1 0. 0 1 0. 2 2 0. 3 0. 6 1. 2 3 0. 9 2. 7 4 0. 1 0. 4 1. 6 1. 0 2. 1 5. 7 d) Compute the expected value of X, E ( X ). (A) 1. 0 (B) 2. 0 (C) 2. 1 (D) 2. 3 e) Compute the standard deviation of X, SD ( X ). (A) 5. 7 (B) 2. 3875 (C) 1. 29 (D) 1. 1358