Random Projection for High Dimensional Data Clustering A

Random Projection for High Dimensional Data Clustering: A Cluster Ensemble Approach Xiaoli Zhang Fern, Carla E. Brodley ICML’ 2003 Presented by Dehong Liu

Contents • Motivation • Random projection and the cluster ensemble approach • Experimental results • Conclusion

Motivation • High dimensionality poses two challenges for unsupervised learning – The presence of irrelevant and noisy features can mislead the clustering algorithm. – In high dimensions, data may be sparse, making it difficult to find any structure in the data. • Two basic approaches to reduce the dimensionality – Feature subset selection; – Feature transformation-PCA, random projection.

Motivation • Random projection – Advantage • A general data reduction technique; • Has been shown to have special promise for high dimensional data clustering. – Disadvantage • Highly unstable. Different random projections may lead to radically different clustering results.

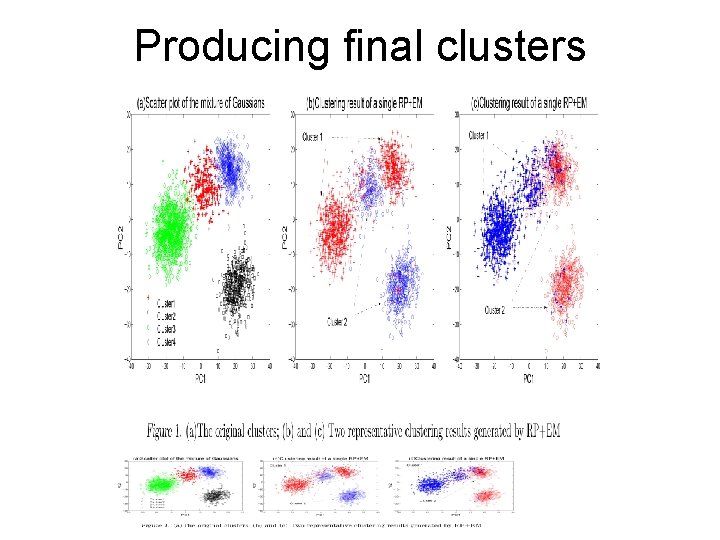
Idea • Aggregate multiple runs of clusterings to achieve better clustering performance. • A single run of clustering consists of applying random projection to the high dimensional data and clustering the reduced data using EM. • Multiple runs of clustering are performed and the results are aggregated to form an n n similarity matrix. • An agglomerative clustering algorithm is then applied to the matrix to produce the final clusters.

A single run • Random projection: X’=X R – X’: n d’, reduced-dimension data set – X : n d , high-dimensional data set – R: d d’, which is generated by first setting each entry of the matrix to a value drawn from an i. i. d N(0, 1) distribution and then normalizing the columns to unit length. • EM clustering

Aggregating multiple clustering results • The probability that data point i belongs to each cluster under the model : • The probability that data point i and j belongs to the same cluster under the model :

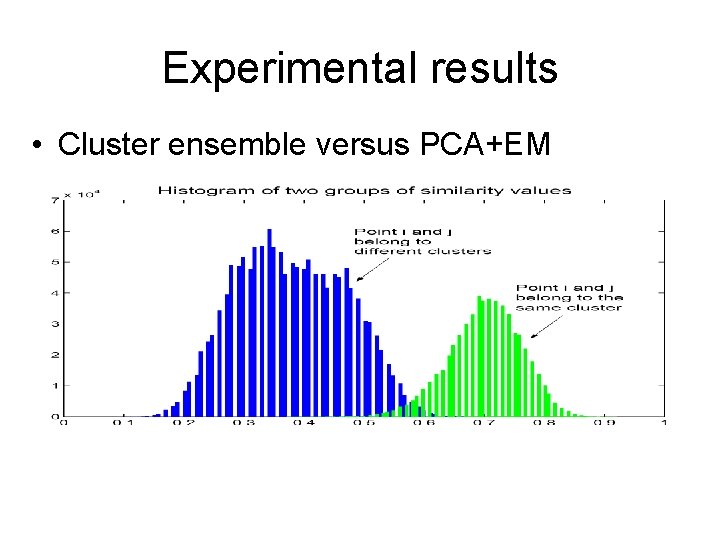
Pij forms a “similarity” matrix.

Producing final clusters

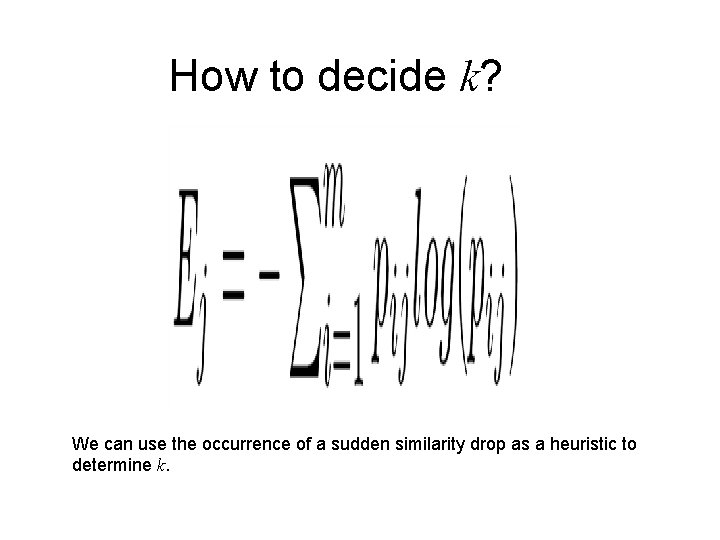
How to decide k? We can use the occurrence of a sudden similarity drop as a heuristic to determine k.

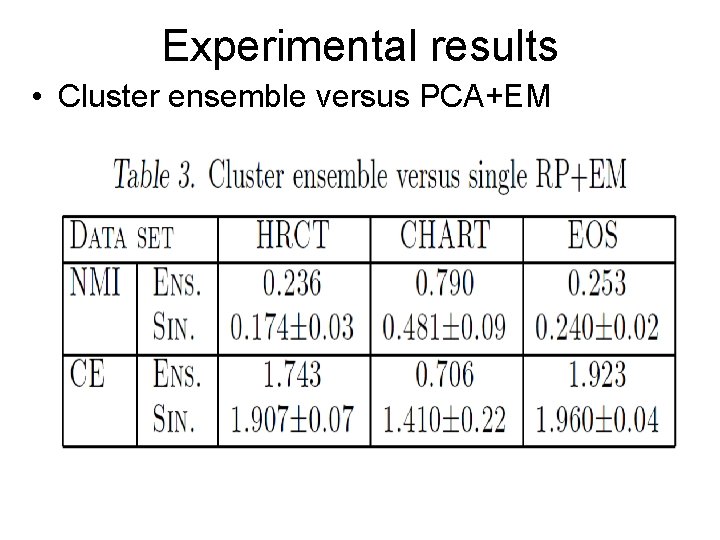
Experimental results • Evaluation Criteria – Conditional Entropy (CE): measures the uncertainty of the class labels given a clustering solution. – Normalized Mutual Information (NMI) between the distribution of class labels and the distribution of cluster labels. – CE: the smaller the better. NMI: the larger the better.

Experimental results • Cluster ensemble versus single RP+EM

Experimental results • Cluster ensemble versus PCA+EM

Experimental results • Cluster ensemble versus PCA+EM

Analysis of Diversity for Cluster Ensembles • Diversity: the NMI between each pair of clustering solutions. • Quality: average the NMI values between each of the solutions and the class labels

Conclusion • Techniques have been investigated to produce and combine multiple clusterings in order to achieve an improved final clustering. • The major contribution of this paper: 1)Examined random projection for high dimensional data clustering and identified its instability problem; 2)formed a novel cluster ensemble framework based on random projection and demonstrated its effectiveness for high dimensional data clustering; and 3) identified the importance of the quality and diversity of individual clustering solutions and illustrated their influence on the ensemble performance with empirical results.