Random Geometric Graphs and Their Applications to Complex

Random Geometric Graphs and Their Applications to Complex Networks BIRS Isomorphism results for infinite random geometric graphs Anthony Bonato Ryerson University

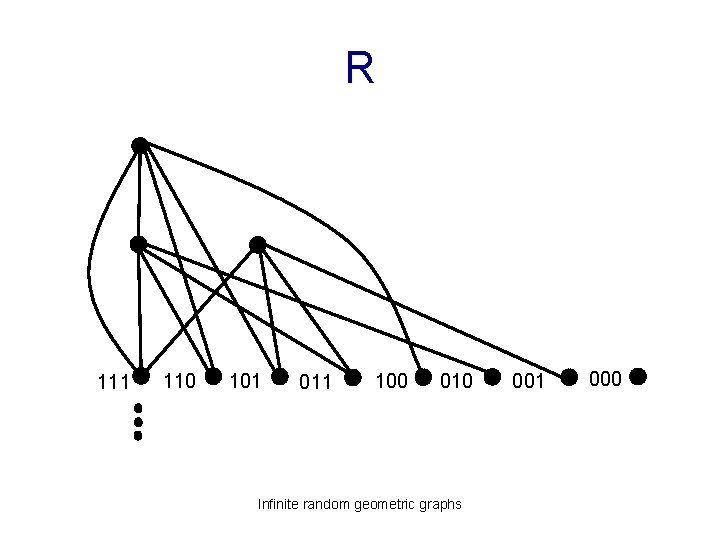
R 111 110 101 011 100 010 Infinite random geometric graphs 001 000

Some properties • limit graph is countably infinite • every finite graph gets added eventually – infinitely often – even holds for countable graphs • add an exponential number of vertices at each time-step – also an on-line construction Infinite random geometric graphs

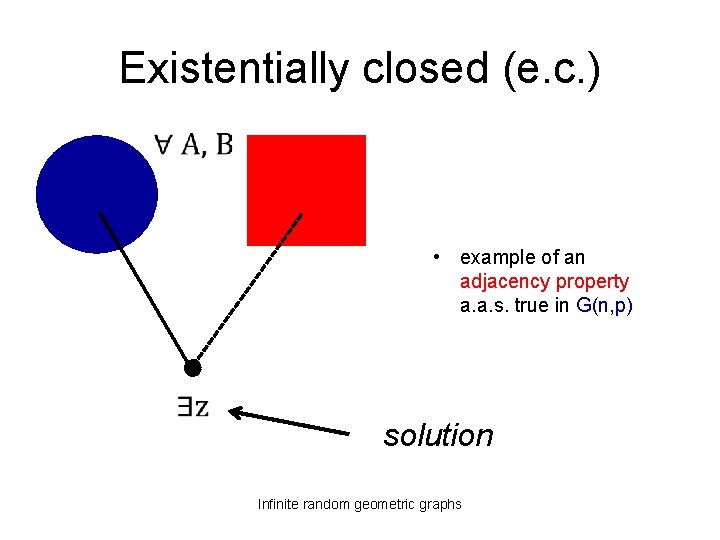
Existentially closed (e. c. ) • example of an adjacency property a. a. s. true in G(n, p) solution Infinite random geometric graphs

Categoricity • e. c. captures R in a strong sense Theorem (Fraïssé, 53) Any two countable e. c. graphs are isomorphic. Proof: back-and-forth argument. Infinite random geometric graphs

Explicit construction • Infinite random geometric graphs

Infinite random graphs • Infinite random geometric graphs

Proof sketch • Infinite random geometric graphs

Properties of R • diameter 2 • universal • indestructible • indivisible • pigeonhole property • axiomatizes almost sure theory of graphs … Infinite random geometric graphs

More on R • A. Bonato, A Course on the Web Graph, AMS, 2008. • P. J. Cameron, The random graph, In: Algorithms and Combinatorics 14 (R. L. Graham and J. Nešetřil, eds. ), Springer Verlag, New York (1997) 333 -351. • P. J. Cameron, The random graph revisited, In: European Congress of Mathematics Vol. I (C. Casacuberta, R. M. Miró-Roig, J. Verdera and S. Xambó-Descamps, eds. ), Birkhauser, Basel (2001) 267 -274. Infinite random geometric graphs

Graphs in normed spaces • Infinite random geometric graphs

Local Area Random Graph (LARG) model • parameters: – p in (0, 1) – a normed space S • V: a countable set in S • E: if || u – v || < 1, then uv is an edge with probability p Infinite random geometric graphs

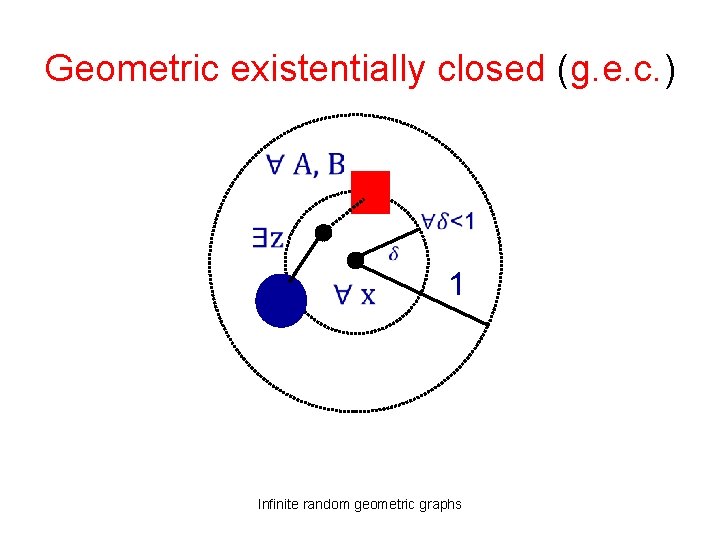
Geometric existentially closed (g. e. c. ) 1 Infinite random geometric graphs

Properties following from g. e. c • locally R • vertex sets are dense Infinite random geometric graphs

LARG is almost surely g. e. c. • geometric 1 -graph: g. e. c. and 1 -threshold: adjacency only may occur if distance < 1 Theorem (BJ, 11) With probability 1, and for any fixed p, LARG generates geometric 1 -graphs. • proof analogous to Erdős-Rényi result for R • geometric 1 -graphs “look like” R in their unit balls, but can have diameter > 2 Infinite random geometric graphs

Geometrization lemma • Infinite random geometric graphs

Step-isometries • Infinite random geometric graphs

Example: ℓ∞ • V: dense countable set in R • E: LARG model • integer distance free (IDF) set – no element is integer – pairwise ℓ∞ distance non-integer • dense sets contain idf dense sets • “random” countable dense sets are idf Infinite random geometric graphs

Categoricity • countable V is Rado if the LARG graphs on it are isomorphic with probability 1 Theorem (BJ, 11) Dense idf sets in ℓ∞d are Rado for all d > 0. • new class of infinite graphs GRd which are unique limit objects of random graph processes in normed spaces Infinite random geometric graphs

Sketch of proof for d = 1 • Infinite random geometric graphs

Properties of GRd • symmetry: – step-isometric isomorphisms of finite induced subgraphs extend to automorphisms • indestructible • locally R, but infinite diameter Infinite random geometric graphs

Dimensionality • Infinite random geometric graphs

Euclidean distance Lemma (BJ, 11) In ℓ 22, every step-isometry is an isometry. • countable dense V is strongly non-Rado if any two such LARG graphs on V are with probability 1 not isomorphic Corollary (BJ, 11) All countable dense sets in ℓ 22 are strongly non-Rado. • non-trivial proof, but ad hoc Infinite random geometric graphs

Honeycomb metric • Theoerem (BJ, 12) Almost all countable dense sets R 2 with the honeycomb metric are strongly non-Rado. Infinite random geometric graphs

Enter functional analysis (Balister, Bollobás, Gunderson, Leader, Walters, 16+) Let S be finite-dimensional normed space not isometric to ℓ∞d. Then almost all countable dense sets in S are strongly non-Rado. • proof uses functional analytic tools: – ℓ∞-decomposition – Mazur-Ulam theorem – properties of extreme points in normed spaces Infinite random geometric graphs

ℓ∞d are special spaces • ℓ∞d are the only finite-dimensional normed spaces with Rado sets • interpretation: – ℓ∞d is the only space whose geometry is approximated by graph structure Infinite random geometric graphs

Questions • classify which countable dense sets are Rado in ℓ∞d • same question, but for finite-dimensional normed spaces • what about infinite dimensional spaces? Infinite random geometric graphs

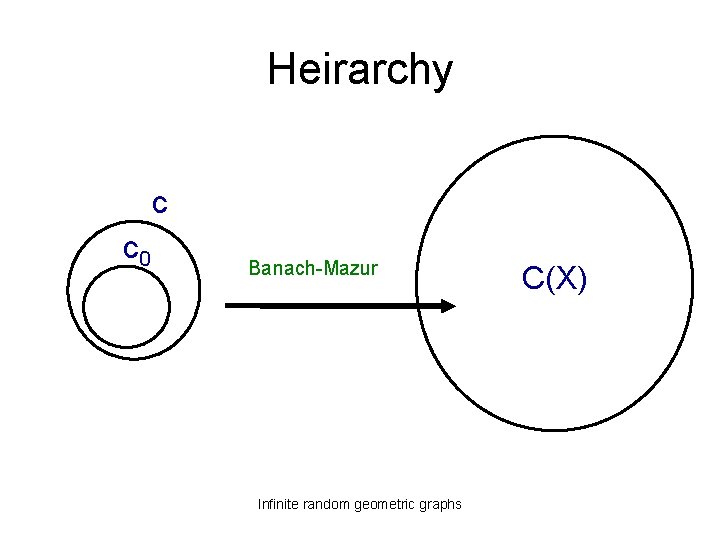
Classical Banach spaces • C(X): continuous function on a compact Hausdorff space X – eg: C[0, 1] • ℓ∞: bounded sequences • c: convergent sequences • c 0: sequences convergent to 0 Infinite random geometric graphs

Separability • a normed space is separable if it contains a countable dense set • C[0, 1], c, and c 0 are separable • ℓ∞ and ω1 are not separable Infinite random geometric graphs

Heirarchy c c 0 Banach-Mazur Infinite random geometric graphs C(X)

Graphs on sequence spaces • fix V a countable dense set in c • LARG model defined analogously to the finite dimensional case • NB: countably infinite graph defined over infinite-dimensional space Infinite random geometric graphs

Rado sets in c Lemma (BJ, Quas, 16+): Almost all countable sets in c are dense and idf. Theorem (BJQ, 16+): Almost all countable sets in c are Rado. Ideas of proof: • Lemma: construct fully supported, non-aligned measures • proof of Theorem somewhat analogous to ℓ∞d • more machinery to deal with the fractional parts of limits of images in back-and-forth argument Infinite random geometric graphs

Rado sets in c 0 Lemma (BJQ, 16+): Almost all countable sets in c 0 are dense, i. d. f. , and satisfy the i. o. p. Theorem (BJQ, 16+): Almost all countable dense in c 0 that are Rado. Ideas of proof: • work in ca • Lemma follows by existence of measures • back-and-forth; i. o. p. acts to “extend collection of dimensions” Infinite random geometric graphs

Geometric structure: c vs c 0 • c vs c 0 are isomorphic as vector spaces • not isometrically isomorphic: – c contains extreme points • eg: (1, 1, …) – unit ball of c 0 contains no extreme points Infinite random geometric graphs

Graph structure: c vs c 0 Theorem (BJQ, 16+) 1. The graphs G(c) and G(c 0) are not isomorphic to any GRn. 2. G(c) and G(c 0) are non-isomorphic. • follows by result of (Dilworth, 99): – δ-surjective ε-isometries of Banach spaces are uniformly approximated by genuine isometries • If geometric 1 -graphs on dense subsets in Banach spaces X and Y give rise to isomorphic graphs, then there is a surjective isometry from X to Y. Infinite random geometric graphs

Questions • almost all countable sets in C[0, 1] are Rado? – if yes, then non-isomorphic to those in c, c 0? • which normed spaces have Rado sets? • program: interplay of graph structure and the geometry of Banach spaces? Infinite random geometric graphs

Contact • Web: http: //www. math. ryerson. ca/~abonato/ • Blog: https: //anthonybonato. com/ • @Anthony_Bonato • https: //www. facebook. com/anthony. bonato. 5 Zombies and Survivors

New book • Graph Searching Games and Probabilistic Methods (B, Pralat, 17+) – Discrete Mathematics and its Applications Series, CRC Press Infinite random geometric graphs

Cana. DAM 2017 Ryerson University Toronto