Random field theory Rumana Chowdhury and Nagako Murase






















![3 rd step Obtain PFWE Expected EC: E[EC] = the probability of finding a 3 rd step Obtain PFWE Expected EC: E[EC] = the probability of finding a](https://slidetodoc.com/presentation_image_h/e2080ded631854465969540a8bf32308/image-32.jpg)
![E[EC]=0. 05 RFT Using this Z score, we can conclude that any blots have E[EC]=0. 05 RFT Using this Z score, we can conclude that any blots have](https://slidetodoc.com/presentation_image_h/e2080ded631854465969540a8bf32308/image-33.jpg)









![Conclusion • By thoresholding, expected EC is calculated by RFT, where PFWE ≒ E[EC] Conclusion • By thoresholding, expected EC is calculated by RFT, where PFWE ≒ E[EC]](https://slidetodoc.com/presentation_image_h/e2080ded631854465969540a8bf32308/image-47.jpg)

- Slides: 48

Random field theory Rumana Chowdhury and Nagako Murase Methods for Dummies November 2010


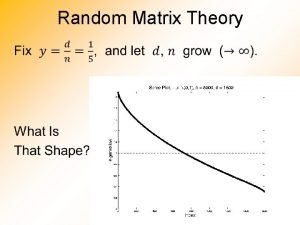
Overview Part 1 • Multiple comparisons • Family-wise error • Bonferroni correction • Spatial correlation Part 2 • Solution = Random Field Theory • Example in SPM

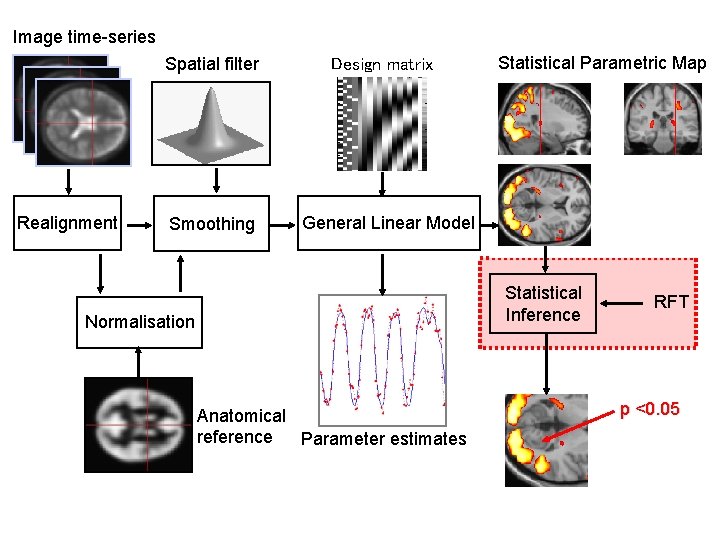
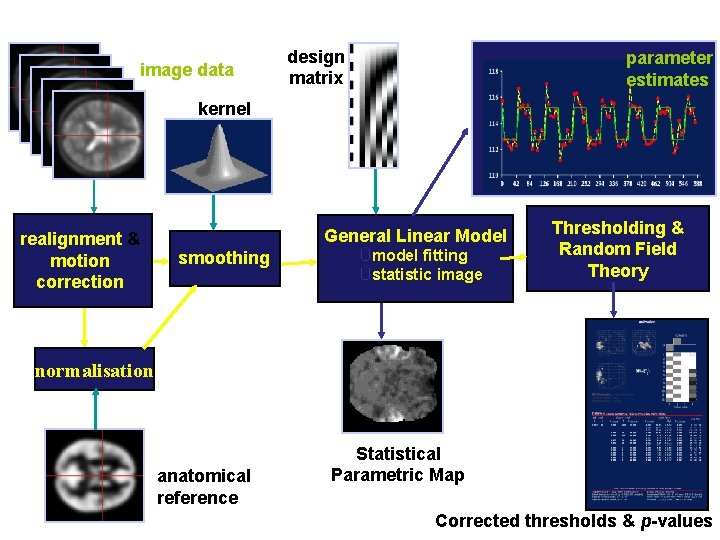
Image time-series Spatial filter Realignment Smoothing Design matrix Statistical Parametric Map General Linear Model Statistical Inference Normalisation Anatomical reference Parameter estimates RFT p <0. 05

Voxel • Raw data collected as group of voxels • 3 D, volumetric pixel – Location – Value • Calculate a test statistic for each voxel • Many many voxels…

Null hypothesis • Determine if value of single specified voxel is significant • Create a null hypothesis, H 0 (activation is zero) = data randomly distributed, Gaussian distribution of noise • Compare our voxel’s value to a null distribution

Single voxel level statistics • Perform t-tests u • Decision rule (threshold) u, determines false +ve rate • Choose u to give acceptable α under H 0 • = P(type I error) i. e. chance we are wrong when rejecting the null hypothesis = p(t>u|H) t

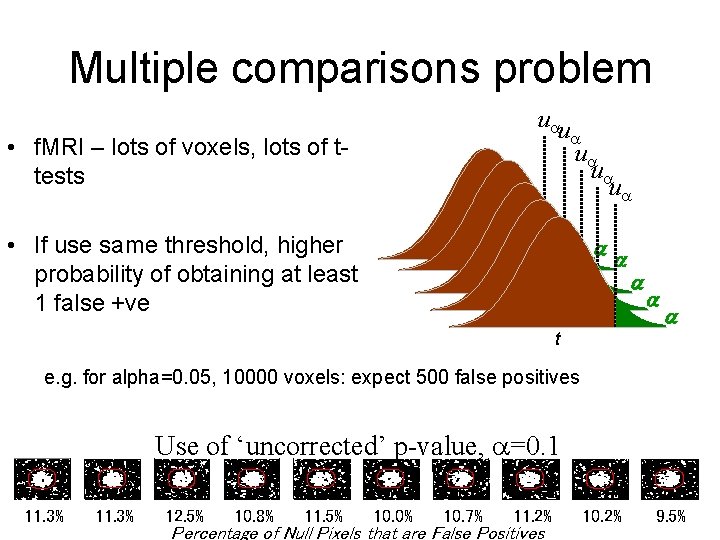
Multiple comparisons problem u u • f. MRI – lots of voxels, lots of ttests • If use same threshold, higher probability of obtaining at least 1 false +ve u u u t t t e. g. for alpha=0. 05, 10000 voxels: expect 500 false positives Use of ‘uncorrected’ p-value, =0. 1 11. 3% 12. 5% 10. 8% 11. 5% 10. 0% 10. 7% 11. 2% Percentage of Null Pixels that are False Positives 10. 2% 9. 5%

Family-wise error • In f. MRI = volume (family) of voxel statistics • Family-wise null hypothesis = activation is zero everywhere • Family Wise Error (FWE) = 1 false positive anywhere • FWE rate = ‘corrected’ p-value Use of ‘uncorrected’ p-value, α =0. 1 Use of ‘corrected’ p-value, α =0. 1 FWE

Definitions Univariate statistics Functional imaging 1 observed data 1 statistical value type I error rate null hypothesis many voxels family of statistical values family-wise error rate (FWE) family-wise null hypothesis

Thresholding • Height thresholding • This gives us localizing power

Bonferroni correction p = /n Corrected p-value α = acceptable Type 1 error rate n = number of tests • The Family-Wise Error rate (FWE), α, for a family of N independent voxels is α = Nv • where v is the voxel-wise error rate. Therefore, to ensure a particular FWE set v=α/N But…

Spatial Correlation • Dependence between voxels : physiological signal data acquisition spatial preprocessing Averaging over one voxel and its neighbours ( independent observations) Usually weighted average using a (Gaussian) smoothing kernel

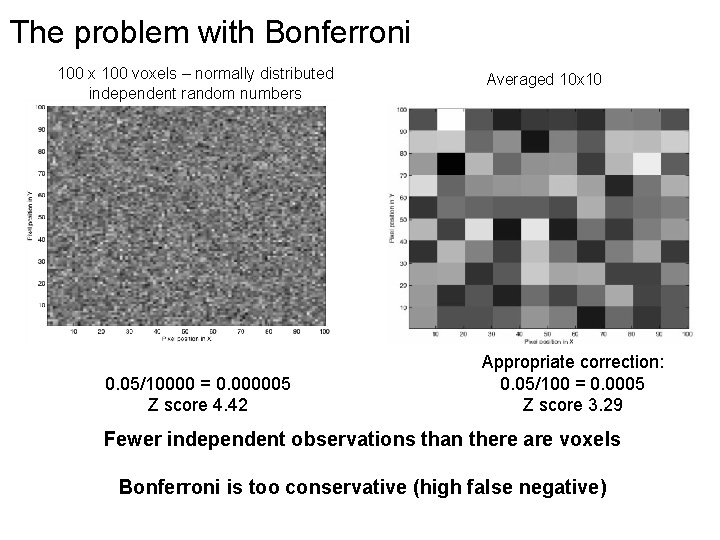
The problem with Bonferroni 100 x 100 voxels – normally distributed independent random numbers 0. 05/10000 = 0. 000005 Z score 4. 42 Averaged 10 x 10 Appropriate correction: 0. 05/100 = 0. 0005 Z score 3. 29 Fewer independent observations than there are voxels Bonferroni is too conservative (high false negative)

• Not making inferences on single voxels • Take into account spatial relationships • Topology

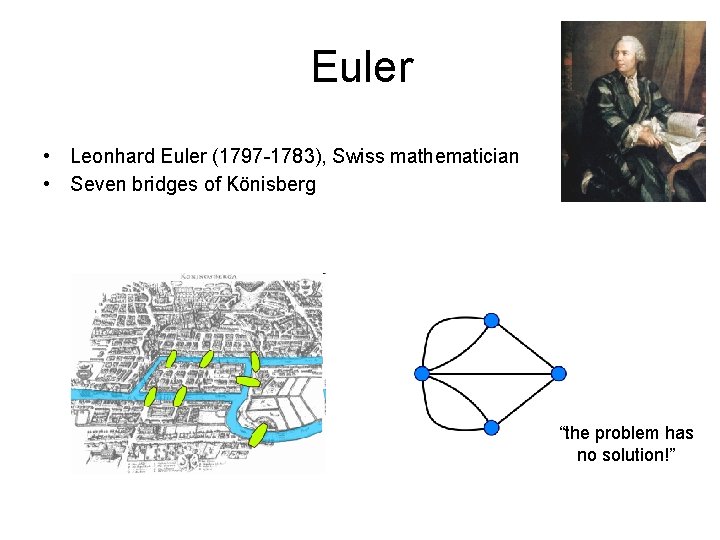
Euler • Leonhard Euler (1797 -1783), Swiss mathematician • Seven bridges of Kӧnisberg “the problem has no solution!”

Euler characteristic: the beginnings • EC V-E+F = 2 • Number of polyhedra (P) V-E+F-P=1 8 – 12 + 6 = 2 16 – 28 + 16 – 3 = 1 • Holes & handles reduce by 1 0 (product of 2 circles) • Topology… 0 d - 1 d + 2 d - 3 d + 4 d…etc EC is a topological measure…

(a little bit more background) • Robert J Adler (1981): relationship between topology of random field (local maxima) and EC • Apply a threshold to random field; regions above = excursion sets • EC is a topological measure of excursion set • Expected EC is a good approximation of FWE at higher threshold • Random field theory uses the expected EC

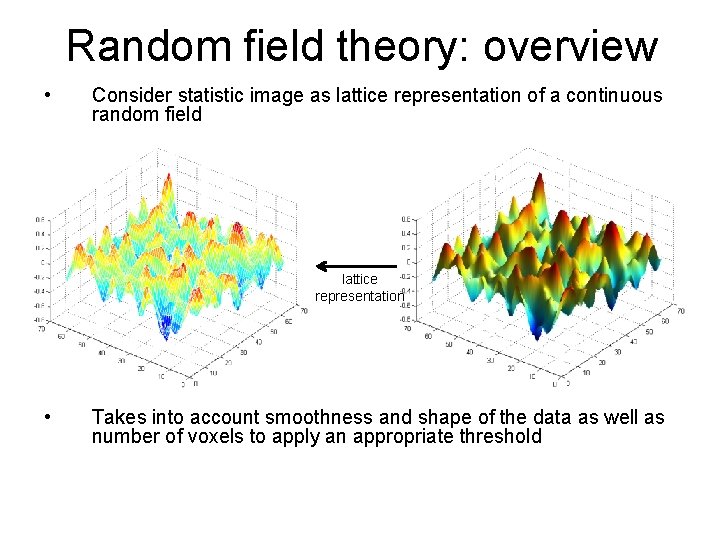
Random field theory: overview • Consider statistic image as lattice representation of a continuous random field lattice representation • Takes into account smoothness and shape of the data as well as number of voxels to apply an appropriate threshold

References • An Introduction to Random Field Theory (Chapter 14) Human Brain Mapping • Developments in Random Field Theory (Chapter 15), KJ Worsley • Previous Mf. D slides: http: //www. fil. ion. ucl. ac. uk/mfd/page 2. html • Guillaume Flandin’s slides: http: //www. fil. ion. ucl. ac. uk/spm/course/slides 10 -meeg/ • Will Penny’s slides: http: //www. fil. ion. ucl. ac. uk/spm/course/slides 05/ppt/infer. ppt#324, 1, Random Field Theory • R. Adler’s website: http: //webee. technion. ac. il/people/adler/research. html • CBU imaging wiki: http: //imaging. mrccbu. cam. ac. uk/imaging/Principles. Random. Fields

Methods for Dummies 2010 Random Field Theory Part II Nagako Murase 17/11/2010 RFT for dummies - Part II 21

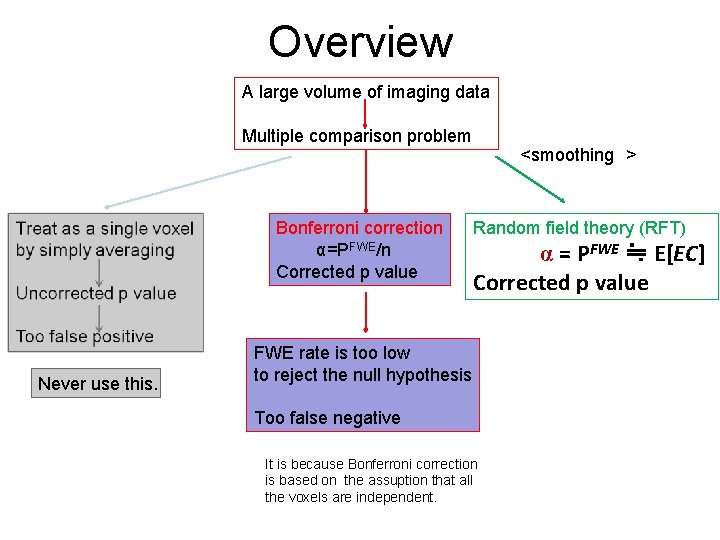
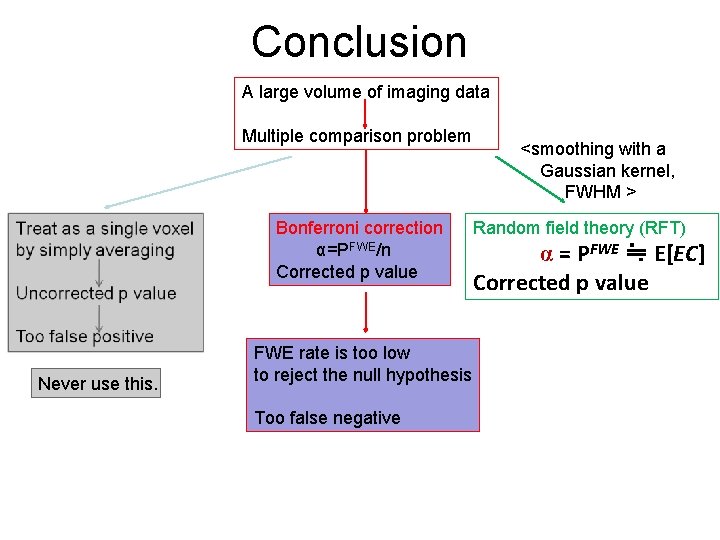
Overview A large volume of imaging data Multiple comparison problem Bonferroni correction α=PFWE/n Corrected p value Never use this. <smoothing > Random field theory (RFT) α = PFWE ≒ E[EC] Corrected p value FWE rate is too low to reject the null hypothesis Too false negative It is because Bonferroni correction is based on the assuption that all the voxels are independent.

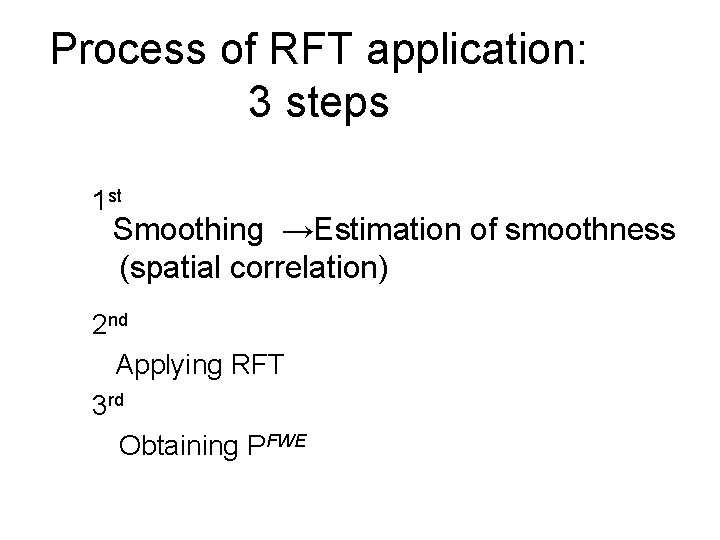
Process of RFT application: 3 steps 1 st Smoothing →Estimation of smoothness (spatial correlation) 2 nd Applying RFT 3 rd Obtaining PFWE

image data design matrix parameter estimates kernel realignment & motion correction General Linear Model smoothing Ümodel fitting Üstatistic image Thresholding & Random Field Theory normalisation anatomical reference Statistical Parametric Map Corrected thresholds & p-values

1 st Smoothing →Estimation of smoothness l By smoothing, data points are averaged with their neighbours. l A smoothing kernel (shape) such a Gaussian is used. l Then each value in the image is replaced with a weighted average of itself and its neighbours. l Smoothness is expressed as FWHM (full width at half maximum) Gaussian curves FWHM Standard Normal Distribution (Probability density function) Mean = 0 Standard Deviation = 1 For example, FWHM of 10 pixels in X axis means that at 5 pixels from the center, the value of the kernel is half of its peak value.

1 st Smoothing →Estimation of smoothness Original data: an image using independent random numbers from the normal distribution After smoothing with a Gaussian smoothing kernel FWHM in x=10, in y=10 so this FWHM=100 pixels)

Resel a block of values, e. g. pixels, that is the same size as the FWHM. u a word made form ‘Resolution Elements’ uone of a factor which defines p value in RFT <example of ressel> The FWHMs were 10 by 10 pixels. Thus a resel is a block of 100 pixels. As there are 10, 000 pixels in our image, there are 100 resels. The number of ressels depend on ü the FWHM ü the number of boxels (pixels).

Smoothing • Compiles the data of spatial correlation. • Reduce the number of independent observations. • Generates a blurred image. • Increases signal-to-noise ratio. • Enables averaging across subjects.

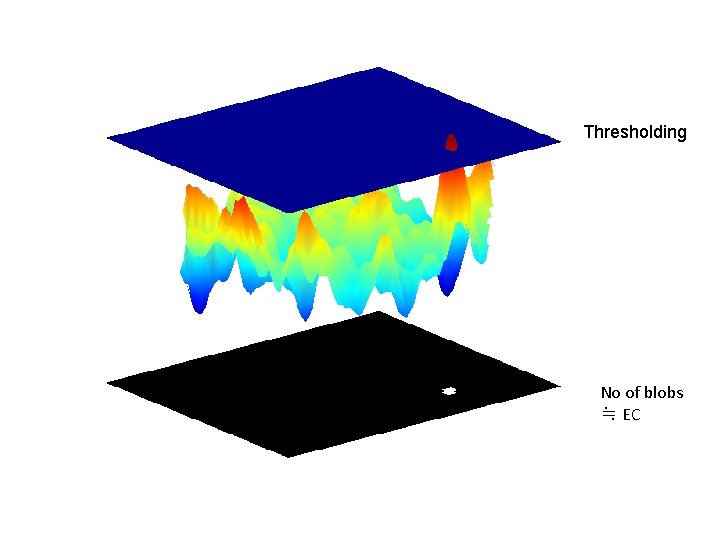
2 nd step Apply RFT After smoothing thresholding Euler characteristics (EC)= the number of blobs (minus number of holes) in an image after thresholding Set the threshold as z core 2. 5 Below 2. 5. . 0. . black Above 2. 5. . 1. . white EC=3

Different Z score threshold generates different EC. z=2. 5 Z=2. 75 EC=3 EC=1

Thresholding No of blobs ≒ EC
![3 rd step Obtain PFWE Expected EC EEC the probability of finding a 3 rd step Obtain PFWE Expected EC: E[EC] = the probability of finding a](https://slidetodoc.com/presentation_image_h/e2080ded631854465969540a8bf32308/image-32.jpg)
3 rd step Obtain PFWE Expected EC: E[EC] = the probability of finding a blob PFWE ≒ E[EC] α = E[EC] = R (4 loge 2) (2π) -3/2 zt exp(-zt 2/2) E[EC] depends on: R the number of resels Zt Z score threshold
![EEC0 05 RFT Using this Z score we can conclude that any blots have E[EC]=0. 05 RFT Using this Z score, we can conclude that any blots have](https://slidetodoc.com/presentation_image_h/e2080ded631854465969540a8bf32308/image-33.jpg)
E[EC]=0. 05 RFT Using this Z score, we can conclude that any blots have a probability of ≦ 0. 05 when they have occured by chance. α=E[EC]=0. 05 Z=3. 8 Bonferroni correction α =0. 05/10, 000=0. 00005 Z=4. 42 If the assumption of RFT are met, then the RFT threshold is more accurate than the Bonferroni correction.

RFT in 3 D • EC=the number of 3 D blobs • Resel=a cube of voxels of size (FWHM in x) by (FWHM in y) by (FWHM in z) • In SPM, the formulae for t, F and χ2 random fields are used to calculate threshold for height. • RFT requires FWHM > 3 voxels 27 Voxels 1 RESEL

RFT Note 1: When FWHM is less than 3. 2 voxels, the Bonferroni correction is better than the RFT for a Gaussian statistic.

RFT Note 2: EC depends on volume shape and size. • EC depends, not only on resel numbers, but also on the shape and size of the volume we want to search (see table). • The shape becomes important when we have a small or oddly shaped regions. V: volume of search region R 0(V): ressel single boxel count R 1(V): ressel radius R 2(V): ressel surface area R 3(V): ressel volume Worsley KJ, et al. , Human Brain Mapping 1996

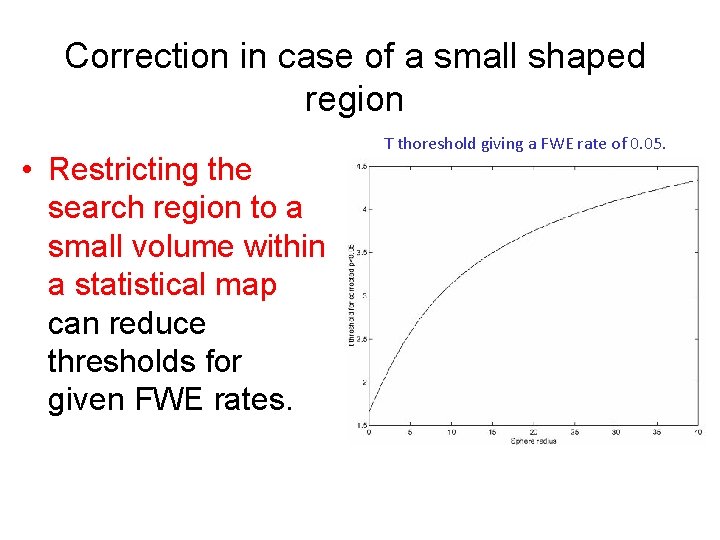
Correction in case of a small shaped region • Restricting the search region to a small volume within a statistical map can reduce thresholds for given FWE rates. T thoreshold giving a FWE rate of 0. 05.

Volume of Interest: EC Diameter Surface Area FWHM=20 mm Threshold depends on Search Volume

Note 3: voxel-level inference → a larger framework inference: different thresholding method • Cluster-level inference • Set-level inference • These framework require üHeight threshold üspatial extent threshold

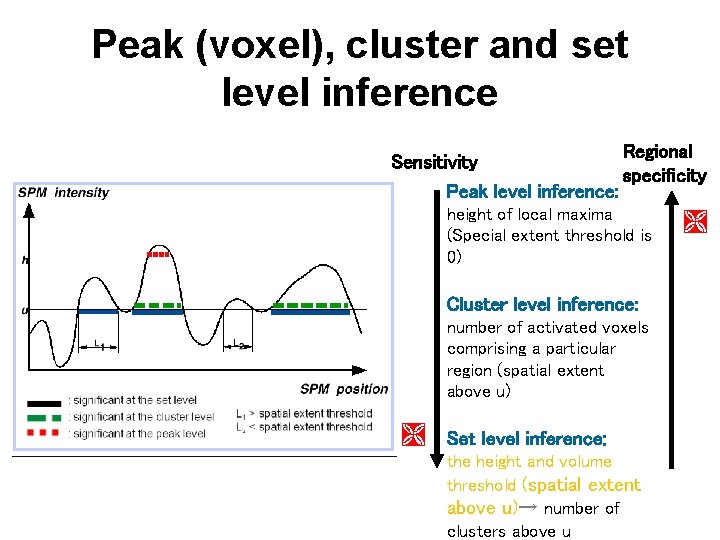
Peak (voxel), cluster and set level inference Regional Sensitivity specificity Peak level inference: height of local maxima (Special extent threshold is 0) Cluster level inference: number of activated voxels comprising a particular region (spatial extent above u) Set level inference: the height and volume threshold (spatial extent above u)→ number of clusters above u

Which inference we should use? • It depends on what you're looking at. • Focal activation is well detected with greater regional specificity using voxel (peak) – level test. • Cluster-level inference – can detect changes missed on voxel-level inference, because it uses the spaticial extent threshold as well.

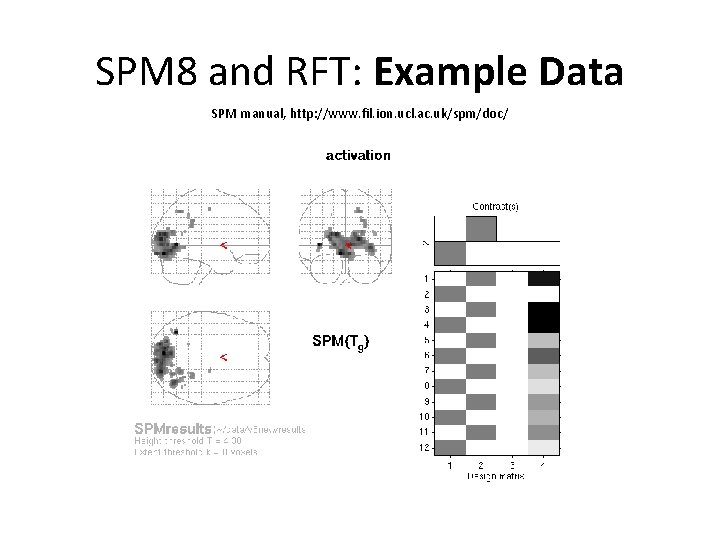
SPM 8 and RFT: Example Data SPM manual, http: //www. fil. ion. ucl. ac. uk/spm/doc/


Random Field Theory: two assumptions q. The error fields are a reasonable lattice approximation to an underlying random field , with a multivariate Gaussian distribution. q. The error fields are continuous. The data can be sufficiently smoothed. The errors are indeed Gaussian and General Linear Models can be correctly specified. RFT assumption is met.

A case where the RFT assumption is not met. Small number of subjects The error fields are not very smooth. üIncrease the subject number üUse Bonferroni correction

Conclusion A large volume of imaging data Multiple comparison problem Bonferroni correction α=PFWE/n Corrected p value Never use this. FWE rate is too low to reject the null hypothesis Too false negative <smoothing with a Gaussian kernel, FWHM > Random field theory (RFT) α = PFWE ≒ E[EC] Corrected p value
![Conclusion By thoresholding expected EC is calculated by RFT where PFWE EEC Conclusion • By thoresholding, expected EC is calculated by RFT, where PFWE ≒ E[EC]](https://slidetodoc.com/presentation_image_h/e2080ded631854465969540a8bf32308/image-47.jpg)
Conclusion • By thoresholding, expected EC is calculated by RFT, where PFWE ≒ E[EC] • Restricting the search region to a small volume, we can reduce threshold for given FWE rates. • FWHM is less than 3. 2 voxels, the Bonferroni correction is better. • Voxel-level and cluster-level inference are used depending on what we are looking at. • In case of small number of subjects, RFT is not met.

Acknowledgement • The topic expert: ØGuillaume Flandin • The organisers: ØChristian Lambert ØSuz Prejawa ØMaria Joao Thank you for your attention!
 Rumana chowdhury
Rumana chowdhury Rumana bukht
Rumana bukht Random field theory
Random field theory Random field theory
Random field theory Md zahidul islam chowdhury
Md zahidul islam chowdhury Md zahidul islam chowdhury
Md zahidul islam chowdhury Pallabi chowdhury
Pallabi chowdhury Zakaria chowdhury
Zakaria chowdhury Prevention of scabies ppt
Prevention of scabies ppt Dr. tamgid ahmed chowdhury
Dr. tamgid ahmed chowdhury Mosharaf chowdhury
Mosharaf chowdhury Dr abhishek chowdhury
Dr abhishek chowdhury Traditional narrative structure
Traditional narrative structure Random assignment vs random sampling
Random assignment vs random sampling Random assignment vs random selection
Random assignment vs random selection Markov random field
Markov random field Asela gunawardana
Asela gunawardana Gauss law of magnetism
Gauss law of magnetism Electric field and magnetic field difference
Electric field and magnetic field difference Data types and field properties
Data types and field properties Field dependent definition
Field dependent definition Magnetic field
Magnetic field Field dependent vs field independent
Field dependent vs field independent Field dependent vs field independent
Field dependent vs field independent Waveguide cutoff frequency
Waveguide cutoff frequency Medan kristal
Medan kristal Forces for change
Forces for change Gestalt psychology
Gestalt psychology Gestalt
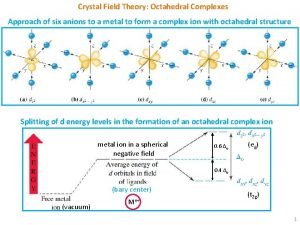
Gestalt Splitting in octahedral complexes
Splitting in octahedral complexes Crystal field theory
Crystal field theory What are the salient features of crystal field theory
What are the salient features of crystal field theory Expectancy value theory of motivation
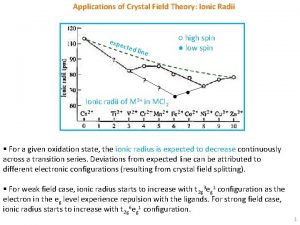
Expectancy value theory of motivation Applications of crystal field theory
Applications of crystal field theory Relativistic mean field theory
Relativistic mean field theory Double revolving field theory
Double revolving field theory Kurt lewin background
Kurt lewin background Dynamical mean-field theory
Dynamical mean-field theory Gauge field theory
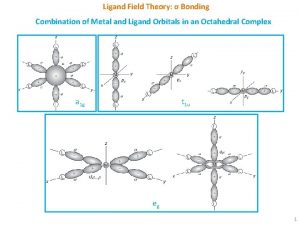
Gauge field theory Ligand field theory
Ligand field theory Field theory kurt lewin adalah
Field theory kurt lewin adalah Theory x and theory y
Theory x and theory y Convergent boundary divergent boundary transform boundary
Convergent boundary divergent boundary transform boundary Continental drift vs plate tectonics theory
Continental drift vs plate tectonics theory Neoclassical organization theory
Neoclassical organization theory Motivation in group formation
Motivation in group formation Hawthorne motivation
Hawthorne motivation Column chromatography theory
Column chromatography theory Title theory and lien theory
Title theory and lien theory