Rancangan Faktorial Factorial Design By Ika Damayanti SSi

Rancangan Faktorial Factorial Design By : Ika Damayanti, SSi, MSi

Rancangan Faktorial è Rancangan faktorial digunakan untuk menyelidiki secara bersamaan efek beberapa faktor berlainan. è Terdapat efek kombinasi dari beberapa faktor è Disebut rancangan faktorial karena : hampir semua faktor dikombinasikan atau disilangkan dengan hampir semua taraf tiap faktor lainnya yang ada dalam eksperimen.

Rancangan Faktorial n Berdasarkan adanya banyak taraf dalam tiap faktor, eksperimen ini sering diberi nama dengan menambahkan perkalian antara banyak taraf faktor yang satu dengan lainnya. n Jika ada a level dari faktor A dan b level dari faktor B, maka terdapat ab kombinasi perlakuan. n Misal dalam eksperimen terdapat 2 faktor, terdiri atas 4 taraf dan 3 taraf, maka diperoleh percobaan faktorial 4 x 3

Main Effect n Perubahan respon (Y) yang diakibatkan dari perubahan level faktor. Misal : n Jika terdapat percobaan faktorial sbb :

Main Effect A n Main effect A didapatkan dari perbedaan rata-rata respon pada level pertama A, dan rata-rata level pada respon kedua A. n A = (40+52)/2 – (20+30)/2 = 21 (kenaikan faktor A dari level 1 ke level 2, mengakibatkan rata-rata respon naik 21 unit)

Main Effect B n Maka : B = (30+52)/2 – (20+40)/2 = 11 (kenaikan faktor B dari level 1 ke level 2, mengakibatkan rata-rata respon naik 11 unit) n *note : n Jika lebih dari 2 faktor, maka definisi diatas tidak bisa digunakan.

Kombinasi antar faktor / Interaksi n perubahan respon dari level suatu faktor terhadap semua level dari faktor lain. n Contoh : n Tabel 2

n Level pertama dari faktor B terhadap efek A adalah : A = 50 -20 = 30 n Level kedua faktor B terhadap efek A adalah : A = 12 – 40 = -28 * (karena efek faktor A tergantung dari pemilihan dari faktor B maka, dapat dikatakan terdapat interaksi/kombinasi antar faktor A dan B)
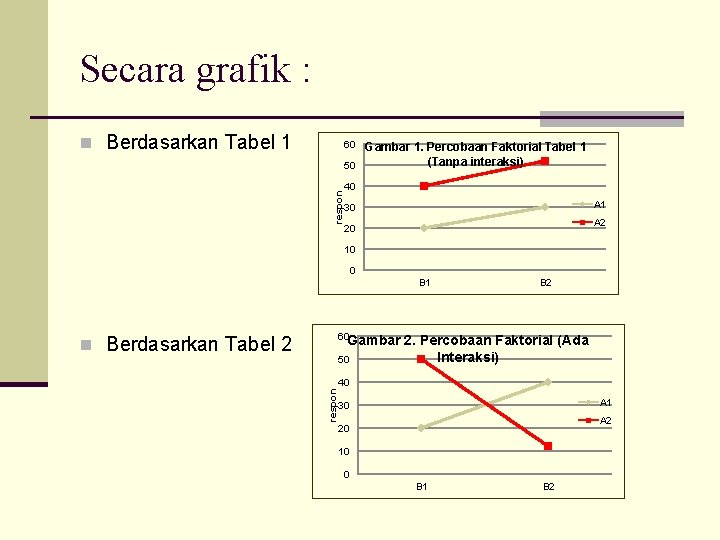
Secara grafik : n Berdasarkan Tabel 1 60 respon Gambar 1. Percobaan Faktorial Tabel 1 (Tanpa interaksi) 50 40 A 1 30 A 2 20 10 0 B 1 B 2 60 Gambar 2. Percobaan Faktorial (Ada Interaksi) 50 n Berdasarkan Tabel 2 respon 40 A 1 30 A 2 20 10 0 B 1 B 2
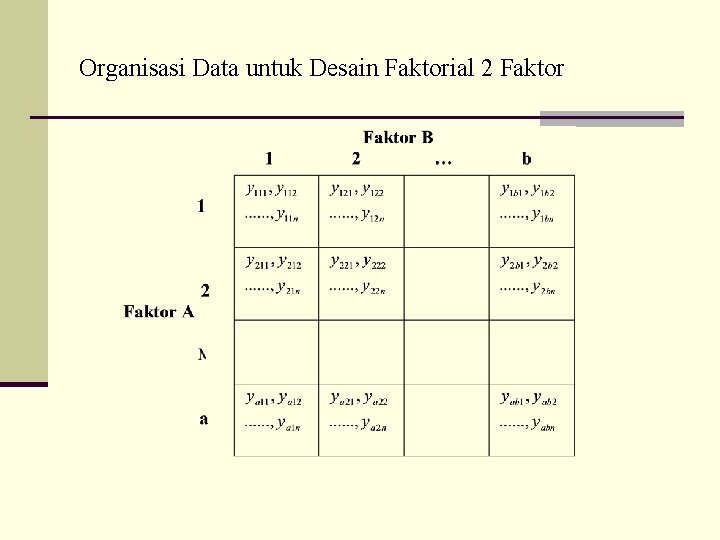
Organisasi Data untuk Desain Faktorial 2 Faktor

Model dari efek tetap: a Level faktor diambil dari A faktor yang tetap, b level faktor diambil dari B faktor yang tetap.

Hipotesis

ANOVA

Model dari efek random a Level faktor A dan b level faktor B diambil dari faktor yang random.

Hipotesis

Perhitungan nilai F (A dan B random)

Model Efek Mixed (Campuran) n Jika A merupakan faktor tetap, dan B merupakan faktor random.

Hipotesis

Perhitungan ANOVA & Uji F n Untuk perhitungan ANOVA, nilai SS, MS sama seperti model efek tetap. n Yang berbeda adalah pengujian F-nya. Perhatikan :

Contoh Latihan n Example 6 -1. (Montgomerry, 1976, pg. 129) n Or n Example 5 -1 (Montgomerry, 2001, pg. 180)

soal n Keluaran maksimum voltase dari beberapa tipe baterai dipengaruhi oleh bahan yang digunakan pada plat dan temperatur di lokasi dimana lokasi baterai tersebut di instal. Empat perulangan dari percobaan faktorial di lakukan di laboratorium dengan tiga material dan tiga temperatur. Hasil percobaan di berikan sebagai berikut :
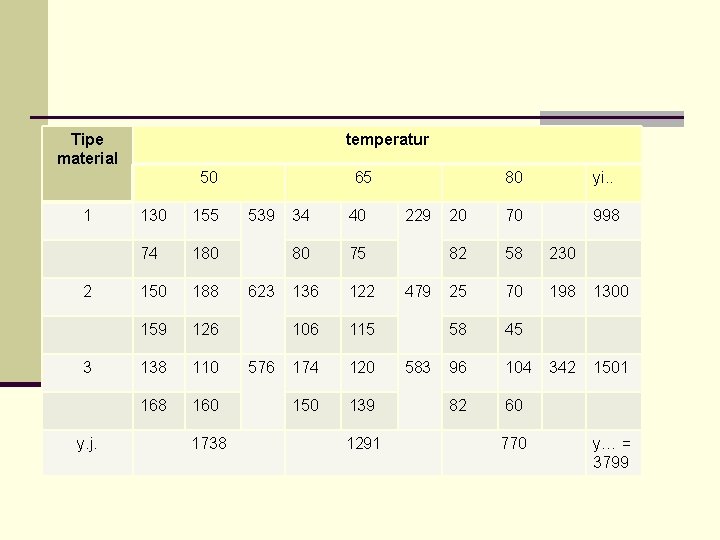
Tipe material temperatur 50 1 2 3 y. j. 130 155 74 180 150 188 159 126 138 110 168 160 1738 65 539 623 576 34 40 80 75 136 122 106 115 174 120 150 139 1291 229 479 583 80 yi. . 20 70 998 82 58 230 25 70 198 1300 58 45 96 104 342 1501 82 60 770 y… = 3799

Rancangan Faktorial Umum n Rancangan faktorial 2 faktor, bisa digeneralisasi menjadi bentuk umum dengan a level dari faktor A, b level dari faktor B, c level dari faktor C, dst… n Sehingga secara umum terdapat abc…n observasi, jika terdapat n pengulangan.

Rancangan Faktorial 3 Faktor

ANOVA untuk Rancangan Faktorial 3 Faktor

Contoh Latihan : n Example 6 -3. (Montgomerry, 1976, pg. 145) Or n Example (Montgomerry, … 2001, pg… )

Latihan (Gunakan Minitab )
- Slides: 27