RAK n Rancangan Acak Kelompok RAK Diterapkan pada

RAK n Rancangan Acak Kelompok (RAK) Diterapkan pada percobaan yang dilakukan pada lingkungan tidak homogen (heterogen) Week 10/11 - 1 / 47

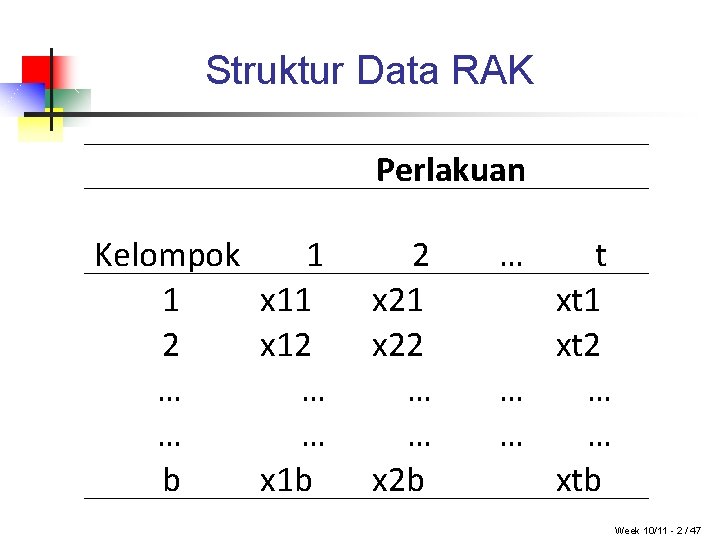
Struktur Data RAK Perlakuan Kelompok 1 1 x 11 2 x 12 … … b x 1 b 2 x 21 x 22 … … x 2 b … t xt 1 xt 2 … … xtb Week 10/11 - 2 / 47

Week 10/11 - 3 / 47

ER untuk memperoleh sensitivitas RAL yang sama dengan RAK maka ulangan yang digunakan dalam menerapkan RAL harus ER kali dari ulangan yang digunakan dalam RAK. Week 10/11 - 4 / 47

FAKTORIAL - RAL Dr. Ir. Rahmat Kurnia, M. Si Week 10/11 - 5 / 47

Two-Way ANOVA n Examines the effect of n Two factors of interest on the dependent variable n n e. g. , Percent carbonation and line speed on soft drink bottling process Interaction between the different levels of these two factors n e. g. , Does the effect of one particular carbonation level depend on which level the line speed is set? Week 10/11 - 6 / 47

Two-Way ANOVA (continued) n Assumptions n Independent random samples are drawn n Populations have equal variances n Populations are normally distributed Week 10/11 - 7 / 47

Two-Way ANOVA Sources of Variation Two Factors of interest: A and B a = number of levels of factor A b = number of levels of factor B r = number of replications for each cell n = total number of observations in all cells (n = abr) Xijk = value of the kth observation of level i of factor A and level j of factor B Week 10/11 - 8 / 47

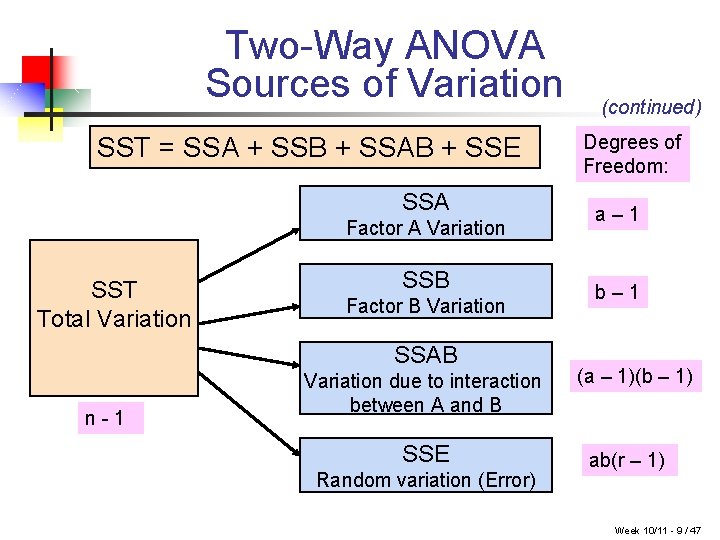
Two-Way ANOVA Sources of Variation SST = SSA + SSB + SSAB + SSE SSA Factor A Variation SST Total Variation SSB Factor B Variation SSAB n-1 Variation due to interaction between A and B SSE Random variation (Error) (continued) Degrees of Freedom: a– 1 b– 1 (a – 1)(b – 1) ab(r – 1) Week 10/11 - 9 / 47

Two Factor ANOVA Equations Total Variation: Factor A Variation: Factor B Variation: Week 10/11 - 10 / 47

Two Factor ANOVA Equations (continued) Interaction Variation: Sum of Squares Error: Week 10/11 - 11 / 47

Two Factor ANOVA Equations (continued) where: r = number of levels of factor A c = number of levels of factor B n’ = number of replications in each cell Week 10/11 - 12 / 47

Mean Square Calculations Week 10/11 - 13 / 47

Two-Way ANOVA: The F Test Statistic H 0: μ 1. . = μ 2. . = μ 3. . = • • • H 1: Not all μi. . are equal H 0: μ. 1. = μ. 2. = μ. 3. = • • • H 1: Not all μ. j. are equal H 0: the interaction of A and B is equal to zero H 1: interaction of A and B is not zero F Test for Factor A Effect Reject H 0 if F > FU F Test for Factor B Effect Reject H 0 if F > FU F Test for Interaction Effect Reject H 0 if F > FU Week 10/11 - 14 / 47

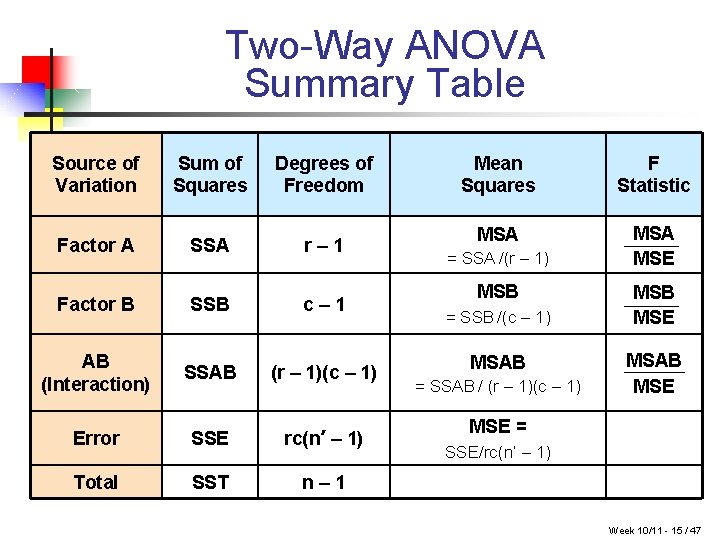
Two-Way ANOVA Summary Table Source of Variation Sum of Squares Degrees of Freedom Factor A SSA r– 1 Factor B SSB c– 1 AB (Interaction) SSAB (r – 1)(c – 1) Error SSE rc(n’ – 1) Total SST n– 1 Mean Squares F Statistic MSA MSE = SSA /(r – 1) MSB = SSB /(c – 1) MSAB = SSAB / (r – 1)(c – 1) MSB MSE MSAB MSE = SSE/rc(n’ – 1) Week 10/11 - 15 / 47

Features of Two-Way ANOVA F Test n n n Degrees of freedom always add up n n-1 = rc(n’-1) + (r-1) + (c-1) + (r-1)(c-1) n Total = error + factor A + factor B + interaction The denominator of the F Test is always the same but the numerator is different The sums of squares always add up n SST = SSE + SSA + SSB + SSAB n Total = error + factor A + factor B + interaction Week 10/11 - 16 / 47

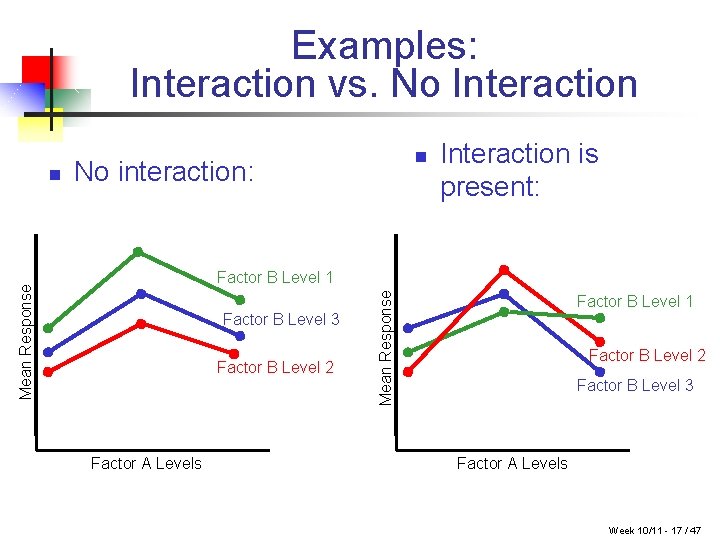
Examples: Interaction vs. No Interaction No interaction: Interaction is present: Factor B Level 3 Factor B Level 2 Factor A Levels Mean Response Factor B Level 1 Mean Response n n Factor B Level 1 Factor B Level 2 Factor B Level 3 Factor A Levels Week 10/11 - 17 / 47

Chapter Summary n n Described one-way analysis of variance n The logic of ANOVA n ANOVA assumptions n F test for difference in c means n The Tukey-Kramer procedure for multiple comparisons Described two-way analysis of variance n Examined effects of multiple factors n Examined interaction between factors Week 10/11 - 18 / 47