Rainbow Graph Designs HungLin Fu Department of Applied

Rainbow Graph Designs Hung-Lin Fu (傅 恒 霖) Department of Applied Mathematics National Chiao Tung University Hsin Chu, Taiwan 30010

Goals n n n The subject we study is to find a special graph design of a properly edge-colored graph; the coloring may be prescribed or arbitrarily given. A good place to start is considering the complete graphs which are properly edge-colored with minimum number of colors, their chromatic indices. If the order of the complete graph is even, this coloring is also known as a 1 -factorization coloring. 2

Preliminaries n A (proper) k-edge-coloring of a graph G is a mapping from E(G) into {1, . . . , k } such that incident edges of G receive (distinct) colors. n In this talk, all colorings are proper, i. e. incident edges receive distinct colors. A proper 3 -edge-coloring of K 4 3

Chromatic Indices It is well-known that the complete graph of order n, Kn, is of Class 1 if and only if n is even. n That is, ’(Kn) = n – 1 if n is even and ’(Kn) = n if n is odd. n A graph G is of Class 1 if its chromatic index is equal to ∆(G) its maximum degree. n 4

Rainbow subgraph n A subgraph H in an edge-colored graph G is a rainbow subgraph of G if no two edges in H have the same color. (A rainbow graph is also known as a multicolored, hetero-chromatic or poly-chromatic graph. ) 3 4 1 5 2 5 4 3 1 2 A rainbow 5 -cycle in a properly edge-colored K 5 5

Motivation n Theorem (Woolbright and Fu, 1998) In any (2 m-1)-edge-colored K 2 m where m > 2, there exists a rainbow 1 -factor. This result has been further improved to complete uniform hypergraphs by Saad El-Zanati et al. later. n It remains unknown for finding two or more edgedisjoint rainbow 1 -factors. n Quite recently, Paul Horn and his student claim that they can find many edge-disjoint rainbow 1 -factors if m is large enough (by using probabilistic method). 6

More Rainbow 1 -factors If we are allowed to design an edgecoloring for K 2 m, then we are able to find (2 m – 1) rainbow 1 -factors inside K 2 m. n This can be done by simply constructing a room square of order 2 m, see example of order 8. n 7

Room square of order 8 1, 8 5, 7 3, 7 2, 8 3, 4 2, 6 6, 1 5, 6 4, 1 3, 8 4, 5 7, 2 6, 7 5, 2 4, 8 2, 4 1, 3 7, 1 6, 3 5, 8 3, 5 1, 2 7, 4 6, 8 4, 6 2, 3 1, 5 7, 8 7 edge-disjoint rainbow matchings! 8

Why rainbow? n Rainbow is beautiful! 9

Taipei City with two rainbows

Prescribed coloring Constantine’s Weak Conjecture (2002) For any m > 2, K 2 m can be (2 m－1)-edgecolored in such a way that the edges can be partitioned into m isomorphic multicolored (rainbow) spanning trees. n This conjecture has been verified later in 2006. (Work jointly with S. Akbari, A. Alipour and Y. H. Lo. ) n 11

Isomorphic rainbow trees in K 6 T 1 T 2 T 3 x 2 Color 1 x 3 x 5 x 4 x 6 x 1 x 2 3 Color 2 x 2 x 4 x 1 x 5 x 3 x 6 x 5 Color 3 x 2 x 5 x 3 x 4 x 1 x 6 1 Color 4 x 2 x 6 x 1 x 3 x 4 x 5 Color 5 x 1 x 4 x 2 x 3 x 5 x 6 2 4 x 6 x 3 x 4 5 x 1 T 1 12

On K 2 m+1 Case n n n Constantine’s Weak Conjecture on odd order (2005) For any m ≥ 2, K 2 m+1 can be (2 m+1)-edge colored in such a way that the edges can be partitioned into m rainbow isomorphic spanning unicyclic subgraphs. Later, we (with Y. H. Lo) verify this conjecture by decomposing K 2 m+1 (with prescribed coloring) into rainbow Hamilton cycles. All 2 m+1 colors occur in a Hamilton cycle. 13

Remark If the edge-coloring is not designed, then finding rainbow spanning trees is not that easy except the first one! 14

Conjectures n Constantine’s Strong Conjecture (2002) If m > 2, then in any properly (2 m－1)-edge-colored K 2 m, all edges can be partitioned into m isomorphic rainbow spanning trees. n Constantine’s Strong Conjecture on odd order (2005) In any properly (2 m+1)-edge-colored K 2 m+1, all edges can be partitioned into m isomorphic rainbow spanning unicyclic subgraphs. n Unicyclic graph: a graph with exactly one cycle. 15

Observation The above two conjectures are too hard to be verified in my opinion. n So, we come back to look at the complete graph with prescribed edge-coloring. n Instead of using up all colors, we consider graph designs where the graph is of small order, say a k-cycle where k is less than the order of the complete graph or certain graph with good structure. n 16

Rainbow cycle designs n n It is easy to see that if Kn (with designed or undesigned edge coloring) can be decomposed into C 3’s, then all C 3’s are rainbow cycles. But, it is not that trivial for C 4 -decomposition even we can design the edge coloring. We expect all cycle decompositions of admissible order and a designed edge coloring, a rainbow cycle design can be obtained. (? ) This is what I am working now: Rainbow cycle designs. 17

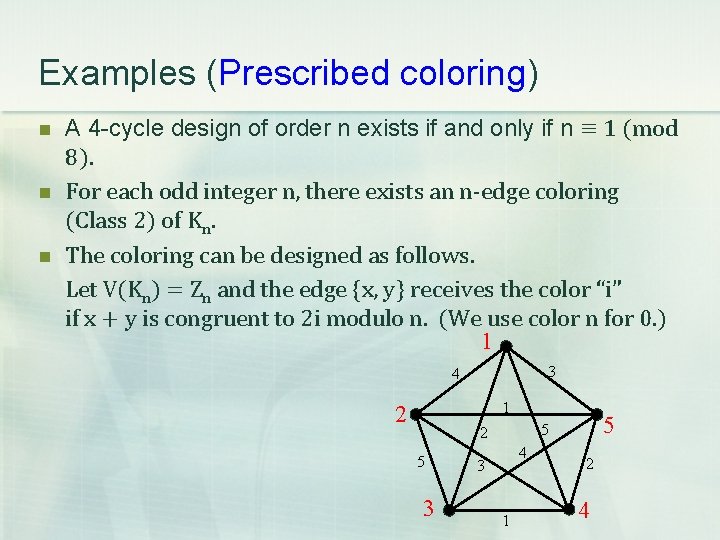
Examples (Prescribed coloring) n n n A 4 -cycle design of order n exists if and only if n ≡ 1 (mod 8). For each odd integer n, there exists an n-edge coloring (Class 2) of Kn. The coloring can be designed as follows. Let V(Kn) = Zn and the edge {x, y} receives the color “i” if x + y is congruent to 2 i modulo n. (We use color n for 0. ) 1 3 4 1 2 5 3 5 5 2 4 3 1 2 4

Cyclic multicolored 4 -cycle system Let n = 8 k + 1, k is a positive integer. n The base cycles are: (3, 4 i+1, 4, 4 i+3), i = 1, 2, …, k. n It is not difficult to check each difference from 1 to 4 k occurs exactly once and the colors in the cycle (3, 4 i+1, 4, 4 i+3) are 2 i + 2, 2 i + 3, 4 k - 2 i - 2 and 4 k - 2 i – 3 which are distinct. n 19

Other cycle-systems? As we have seen rainbow cycle systems of order n do exist when the cycle lengths are 4 and n. n Problem: Find a rainbow cycle system for each cycle length larger than 4. n Example: For the same edge-coloring, (0, 3, 8, 10, 11, 4) generates a rainbow 6 cycle system of order 13. (Make sure this cycle is a base cycle and a rainbow cycle. ) n 20

Recent progress For h, t N, there exists a rainbow 4 hcycle design of order 8 ht + 1. (k = 4 h) n If k is a prime power of 2 (k > 2), then a rainbow k-cycle design of order n exists if and only if n 1 (mod 2 k). n For each k 3 (mod 4), there exists a rainbow k-cycle design of order 2 k + 1. n (*) The idea is to find a suitable labelling of the cycle we consider. n 21

Notation For convenience, we shall use H |R G to denote the existence of a rainbow Hdesign of G. If G is Kn, we say that a rainbow H-design of order n exists. n If H is a path which is not too long comparing to n, then it is not difficult to verify that a rainbow H-design of order n exists as long as n(n-1)/2 is multiple of the length of H. (? ) n 22

Rainbow cycle designs of K 2 m, 2 m Ch |R Kht, ht for each h 0 or 2 (mod 4), t N. n With the aid of this fact, we can obtain more rainbow cycle designs where the cycle length is odd. n This is by the standard construction of combining H | K 2 m+1 and H | K 2 m, 2 m. n 23

Problems I would like to work! n n Construct a rainbow k-cycle design for each admissible order? Here, the edge-coloring is prescribed. Can we do it if the edge-coloring is arbitrarily given? k = 3 is an exception. We are able to prove that if for each t ≥ 3 a strong rainbow 4 -cycle design of order 8 t + 1 exists at this moment. (The edge-coloring is arbitrarily given. ) How about t = 1 and 2? 24

Reference [1] S. Akbari, A. Alipour, H. L. Fu and Y. H. Lo, Multicolored parallelisms of isomorphic spanning trees, SIAM J. Discrete Math. 20 (2006), No. 3, 564567. [2] G. M. Constantine, Multicolored parallelisms of isomorphic spanning trees, Discrete Math. Theor. Comput. Sci. 5 (2002), No. 1, 121 -125. [3] G. M. Constantine, Edge-disjoint isomorphic multicolored trees and cycles in complete graphs, SIAM J. Discrete Math. 18 (2005), No. 3, 577 -580. [4] H. L. Fu and Y. H. Lo, Multicolored parallelisms of Hamiltonian cycles, Discrete Math. 309 (2009), No. 14, 4871 -4876. [5] H. L. Fu and D. E. Woolbright, On the existence of rainbows in 1 factorizations of K 2 n, J. Combin. Des. 6 (1998), 1 -20. [6] H. L. Fu, Rainbow cycle designs, in preprints. 25

Thank you for your attention! 26