Railway Curves Why to know about curve Open

Railway Curves

Why to know about curve ? • Open Line: - Inspection, Maintenance, Correction - Renewal of Sleepers and Rail • Construction: - Designing a Curve - Laying of Curve Reference: must read chapter -4 of IRPWM

What is a Curve ? § a line, which is not straight; and § changes direction without angles (No sharp Edges); or § line, which gradually deviates from being straight
Apex Distance Option I (Min. Radius) Optimum Option II (Max. Radius) Choosing Appropriate Curve

Effects of curve: Centrifugal force • Undesirable Effects – Risk of vehicle overturning – Possible passenger discomfort – Possible displacement of loads – Risk of derailment – Higher Lateral forces on track structure – Higher lateral forces resulting in maintenance problems – Wear of rail & wheel flange

Design Parameters of Curves • Radius, R and Degree of Curve, D • Actual Cant (Super-elevation), Ca • • • Equilibrium Cant, Ce / Equilibrium Speed, Ve Cant Deficiency, Cd Cant Excess, Cex Rate of Change of Actual Cant, RCa Rate of Change of Cant Deficiency, RCd Cant Gradient, i • Length of Transition, L

Curve Designation • On IR: degree of curve for designation – Radii For Calculation
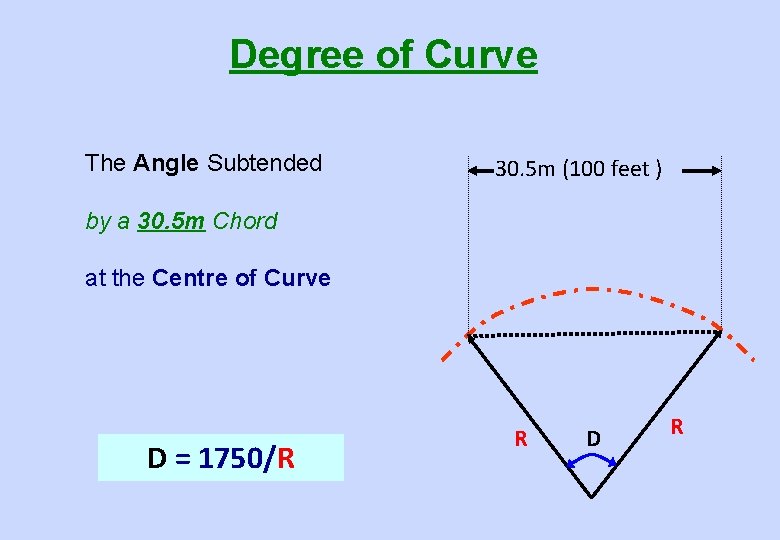
Degree of Curve The Angle Subtended 30. 5 m (100 feet ) by a 30. 5 m Chord at the Centre of Curve D = 1750/R R D R
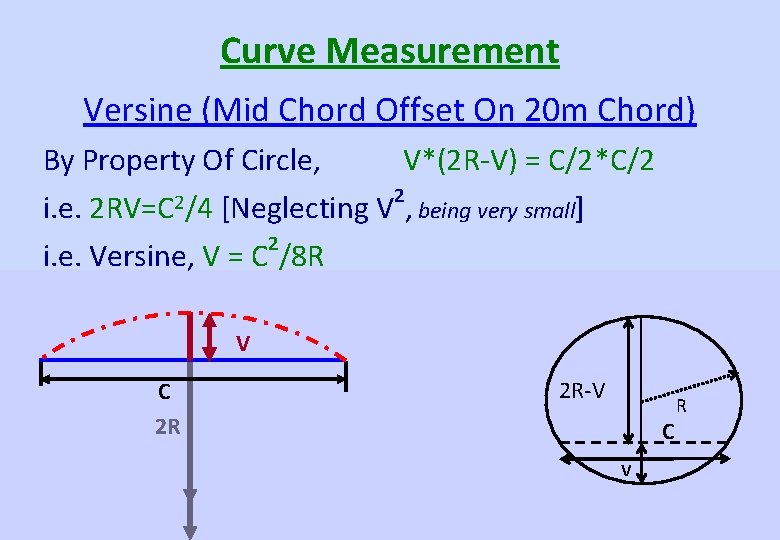
Curve Measurement Versine (Mid Chord Offset On 20 m Chord) By Property Of Circle, V*(2 R-V) = C/2*C/2 2 2 RV=C 2/4 i. e. [Neglecting V , being very small] 2 i. e. Versine, V = C /8 R V C 2 R 2 R-V C V R

Limiting radii on IR • BG* : 175 M • MG: 109 M • NG: 44 M *Item 2, Chapter I, Schedule I of SOD

Super-elevation/Cant

Super-elevation/Cant • Raising of the outer rail (w. r. t. Inner Rail) to counter the effect of Centrifugal Force (elimination/reduction) is known as Super-elevation/ Cant

Equilibrium Cant/Speed • When on circular motion • If the resultant of Weight & Centrifugal Force is perpendicular to the plane of rail & passes through the centre of track i. e load on both the rails is equal The corresponding speed is known as Equilibrium Speed; and cant is known as Equilibrium Cant

Equilibrium Cant Weight Component = W*sinθ (Along plane joining rail heads) Centrifugal Force Comp. = M*(V 2/R) i. e. W*sinθ = M*(V 2/R) i. e. M*g*SE/G = M*V 2/R i. e. Equilibrium Cant, SE=G*V 2/(g*R) SE=G*V 2/(127*R) Para 406(a) of IRPWM

Considerations of Mixed Traffic • For what speed should the cant be provided ? – Maximum speed ? – Minimum Speed ? – Average Speed?

Equilibrium Speed • Schramm’s Formula: • Li • Vi • n : Load of ith train, : Speed of ith train, : Number of trains

Equilibrium Speed • Russian Formula: • • ni Wi Vi m : No of trains of type i, : Weight of such train, : Speed of such train, : Total types of trains

Equilibrium Speed • IRPWM Stipulations (Para 406(b)) Equilibrium speed is to be decided by CE considering • Max. Speeds of fast & slow moving trains (actually attainable) • Proximity to Permanent speed restriction • Junctions • Stopping places • Gradient affecting speed of goods train

Limitations on Maximum value of Actual Cant Ca • Comfort criteria – Maximum discomfort when stopped at Canted Track – No appreciable discomfort upto 180 mm • Limited to 1/8 to 1/10 of Track Gauge
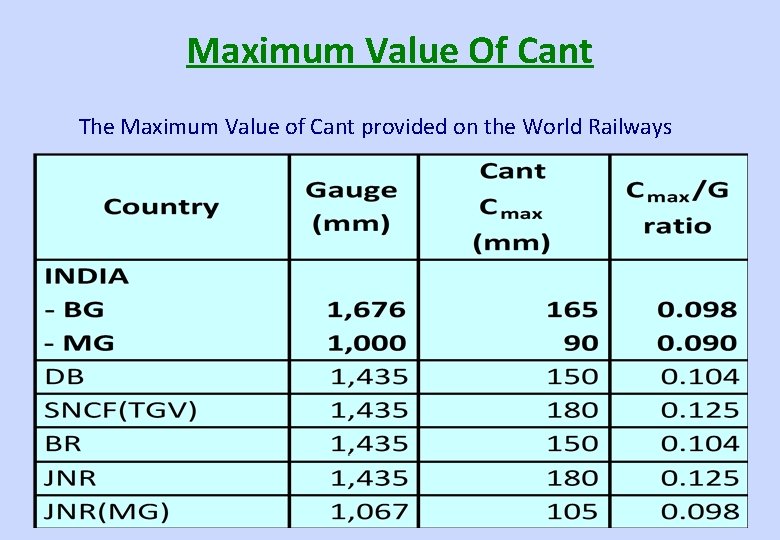
Maximum Value Of Cant The Maximum Value of Cant provided on the World Railways

IRPWM Provisions • Maximum Cant (Para 406(1)(d)(i)) – 165 mm for group A, B and C routes • 185 MM for locating permanent structures on group A routes with speed increase potential (new works and doubling) – 140 mm for group D and E routes

Cant Deficiency: Fast Trains

Effects Of Vehicle With Cant Deficiency Speed more than equilibrium speed Centrifugal Force Component > Weight Component • Creq > Ca • Cd = Creq - Ca θ • R o > R i SE G θ • More wear on outer rail gauge face

Criteria for Cant Deficiency Cd • Safety (overturning about the outer Rail) – Larger values can not be permitted – not governing criteria • Comfort criteria* – Discomfort, if Unbalanced Lateral Acceleration is greater than 0. 1 g • UIC recommends 0. 4 m/s 2 to 0. 7 m/s 2 – (1. 0 m/s 2 to 1. 5 m/s 2 for fast passenger trains UIC 703 -R) • SNCF/TGV adopted 0. 56 m/s 2 (trials 0. 7 m/s 2 )
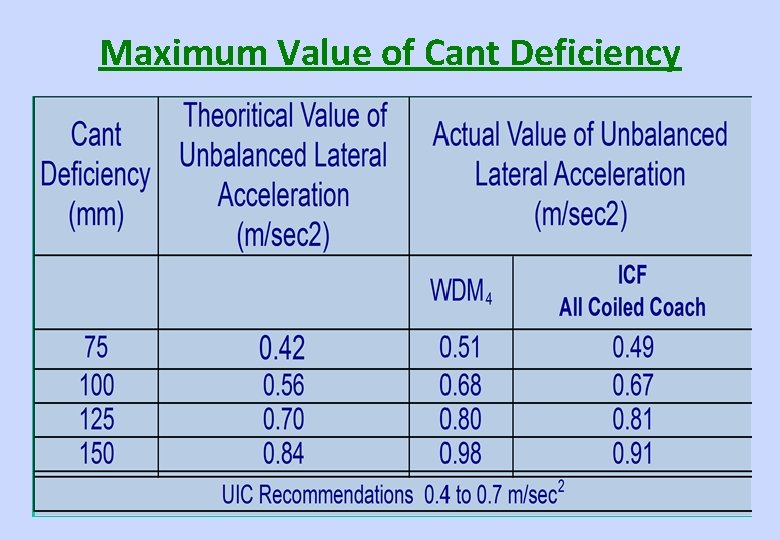
Maximum Value of Cant Deficiency

IRPWM Provisions • Max. Cant Deficiency (Para 406(2)) • On routes – with track maintained to C&M, Vol-I standard; – For Nominated Rolling Stock; – With Permission of PCE : 100 mm – For Other cases : 75 mm

Cant Excess: Slow Trains

Effects Of Vehicle With Cant Excess Speed less than equilibrium speed Centrifugal force Component < Weight Component • Creq < Ca • Cex = Ca - Creq θ • R i > R o SE G θ • More wear on inner rail top table

IRPWM Provisions • Max. Cant Excess - 75 mm (Para 406(3)) – Sections carrying predominantly goods traffic shall have less cant excess to reduce wear on inner rail – Worked out for booked speed of goods trains.

Transition Curves

Transition Curves An easement curve, introduced between straight & curved track to facilitate gradual change of Curvature & Super-elevation from Straight Track to Curved Track

Requirements from Transition Curves • Curvature shall vary uniformly with distance – Curvature = 1/R – Versine shall vary uniformly • Cant shall vary uniformly • Transition shall be tangential to the straight as well as circular curve – Radius infinity at junction with straight – Radius R at junction with circular curve
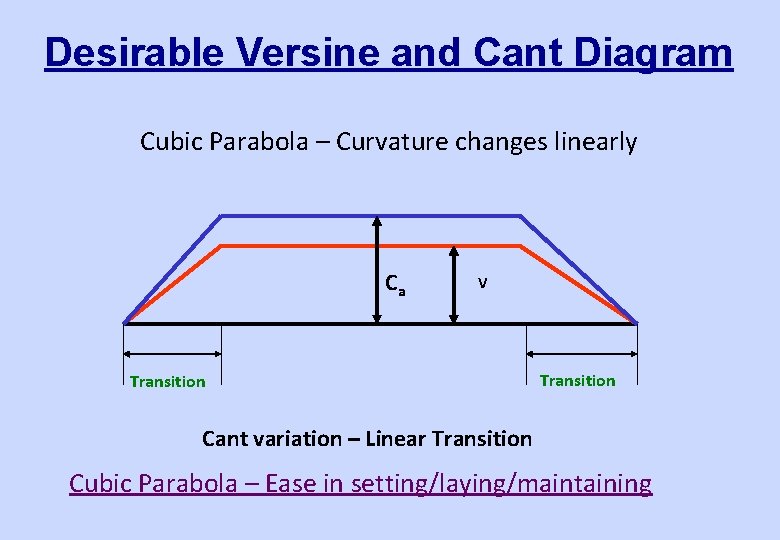
Desirable Versine and Cant Diagram Cubic Parabola – Curvature changes linearly Ca V Transition Cant variation – Linear Transition Cubic Parabola – Ease in setting/laying/maintaining

Transition Curves • The spiral (Clothoid), which changes the direction angle uniformly along length, is the ideal transition –i. e. L ∝ 1/R • Cubic Parabola – rate of change of curvature uniform with the distance on X direction –i. e. X ∝ 1/R

Transition Curves • There is not much difference in the layout of a spiral and cubic parabola until the deflection from straight is approximately 4 M and deviation angle upto 12° • On Indian Railways for Transition Curves, it is cubical parabola with the equation: Y = KX 3 (Y= X 3/6 R*L)

How to decide a curve
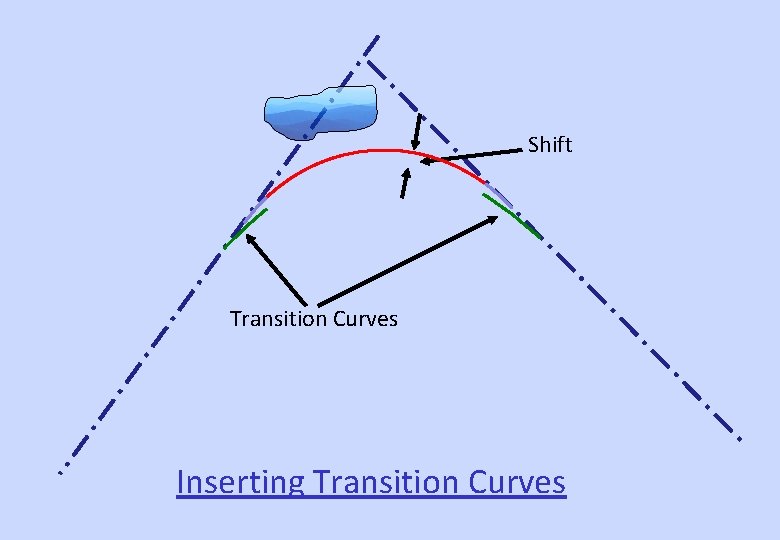
Shift Transition Curves Inserting Transition Curves
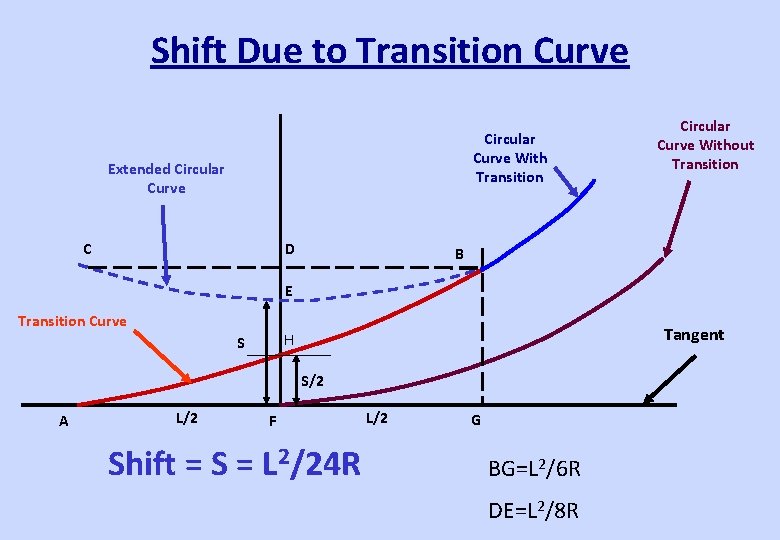
Shift Due to Transition Curve Circular Curve With Transition Extended Circular Curve C D Circular Curve Without Transition B E Transition Curve Tangent H S S/2 A L/2 F Shift = S = L 2/24 R L/2 G BG=L 2/6 R DE=L 2/8 R

Length of Transition Curve
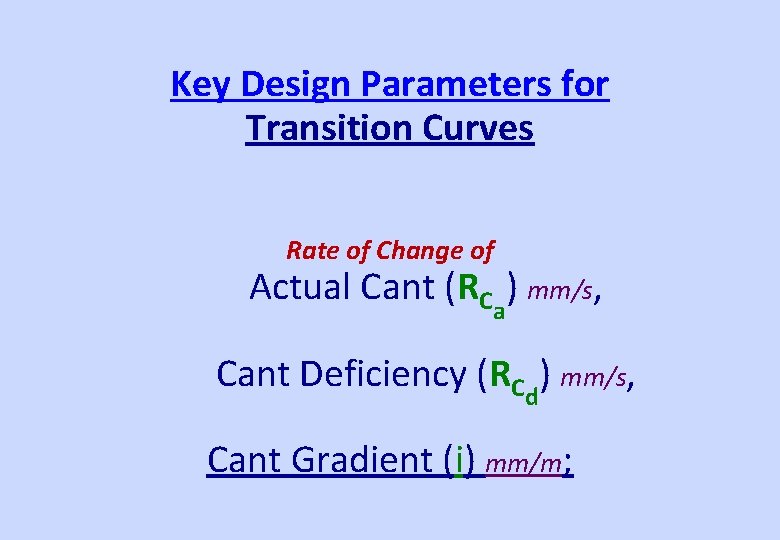
Key Design Parameters for Transition Curves Rate of Change of Actual Cant (RCa) mm/s, Cant Deficiency (RCd) mm/s, Cant Gradient (i) mm/m;

Length of Transition Curve • Comfort Criteria: Rate of Change of Cd (RCd) – Rate of Change of ULA less than 0. 03 g / s taken as 0. 3 m/s 3 – Rate of Change of Cd over Transition where,

Length of Transition Curve • Comfort Criteria: • Rate of Change of Cd (RCd) and Rate of Change of Ca (RCa) – Rate of Change of Cd or Ca , normally shall not exceed 35 mm/sec – Under Exceptional Circumstances it can be increased to 55 mm/sec

Length of Transition Curve • Safety Criteria (Twist) – Cant gradient causes twist in track – Critical - longest rigid wheel base – Cant gradient (i) • Limited to 1. 4 mm/m or 1 in 720 • In Exceptional Cases 2. 8 mm/M or 1 in 360 • Future Layouts with 1 in 1200

Length of Transition Curve • Length of transition will be maximum of L 1 = C a * V m / R Ca or L 2 = C d * V m / R Cd or L 3 = Ca / i

Length of Transition Curve • Length of transition will be maximum of L 1 = 0. 008 Ca* Vm (m, mm, kmph, RCa=35 mm/s) L 2 = 0. 008 Cd*Vm (m, mm, kmph, RCd=35 mm/s) L 3 = 0. 72 Ca (m, mm, i = 1 in 720) or or

Length of Transition Curve • In exceptional circumstances, minimum length of transition will be maximum of 2/3 rd of L 1 or 2/3 rd of L 2 or ½ of L 3
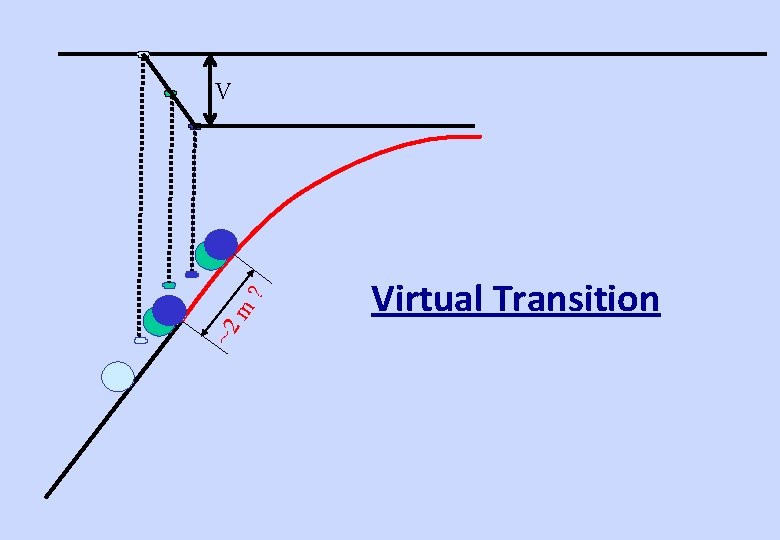
~2 m ? V Virtual Transition

Virtual Transition • If there is no space for transition, circular curve immediately follows the straight, the distance between bogie centers becomes the transition virtually • For BG • For MG - 14. 785 M - 13. 7 M • Cant is provided in virtual transition length • half in straight and half in circular curve • @1 in 360 (max. cant gradient) max. cant = 14. 6 * 2. 8 = 40 mm
Reverse and Compound Curves

Reverse Curves Length of intermediate Transition will be Maximum of L 1 = 0. 008 * (Ca 1+Ca 2) * Vm L 2 = 0. 008 * (Cd 1+Cd 2) * Vm L 3 = 0. 72 * (Ca 1+Ca 2) Constant roll velocity during intermediate transition

Reverse Curves • For high speeds in Group A and B routes a straight of 50 m length shall be kept – One cycle of oscillation for passenger coach (1. 5 sec) • Otherwise, increase the transition length to eliminate the straight • If neither of the above two are possible than speed restriction of 130 KMPH on BG

Compound Curves

• For Compound Curves: Length of Intermediate Transition shall be Maximum of • L 1 = 0. 008 * (Ca 1 - Ca 2) * Vm • L 2 = 0. 008 * (Cd 1 - Cd 2) * Vm • L 3 = 0. 72 * (Ca 1 - Ca 2) If length is coming less than virtual transition then common transition is deleted and the cant is run out on the length of virtual transition

Vertical curves
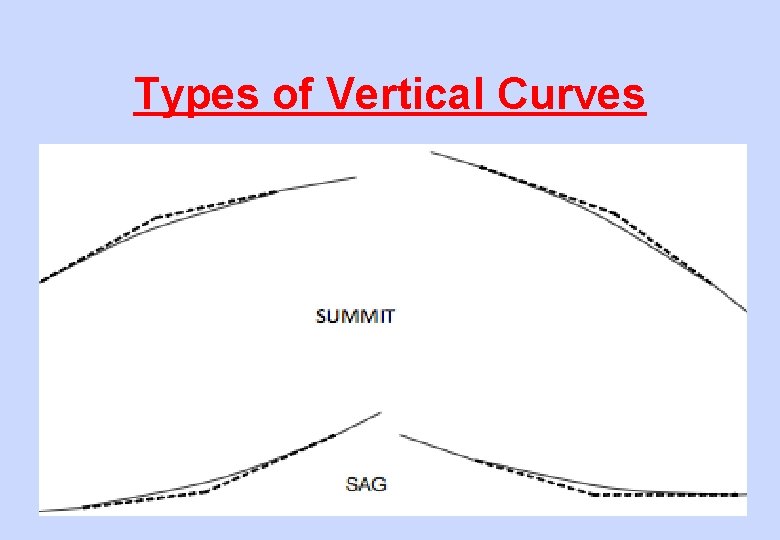
Types of Vertical Curves

Vertical curves • Vertical Curves to be provided, if ; Algebraic Difference between the Grades ≥ 0. 4% (4 mm/m) • Not allowed in –Points and Crossing –Un-ballasted deck girder bridges –Transition portion of horizontal curves

Vertical curves • Important issues – Vertical acceleration – Drainage (Sag) – Ventilation (Summit) in Tunnels ?

Vertical curves • Shall be as flat as possible to reduce Discomfort to passengers • Vertical Acceleration 0. 3 – 0. 45 m/s 2 2 • Radius Rv ≥ Vm / am Route A B C, D, E & MG Minimum Radius (m) 4, 000 3, 000 2, 500

Thank You
- Slides: 59