RAGHU ENGINEERING COLLEGE AUTONOMOUS DEPARTMENT OF MECHANICAL ENGINEERING

• RAGHU ENGINEERING COLLEGE (AUTONOMOUS) DEPARTMENT OF MECHANICAL ENGINEERING Mechanics of solids UNIT-4: DEFLECTION OF BEAMS Prepared by Mr. Singuru Rajesh Assistant Professor Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 1

Ø CONTENTS: § § § Bending into a circular arc Slope, deflection and radius of curvature Differential equation for the elastic line of beam Double integration Method Macaulay’s method Determination of Slope, Deflection for Cantilever and Simply Supporting Beams § Determination of Slope, Deflection for Cantilever and Cantilever Beams DEFLECTION OF BEAMS Bending into a circular arc – slope, deflection and radius of curvature –Differential equation for the elastic line of a beam – Double integration and Macaulay’s methods – Determination of slope and deflection for cantilever and simply supported beams subjected to point loads, - U. D. L uniformly varying load. Mohr’s theorems – Moment area method – application to simple cases including overhanging beams, Statically Indeterminate Beams and solution methods. Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 2

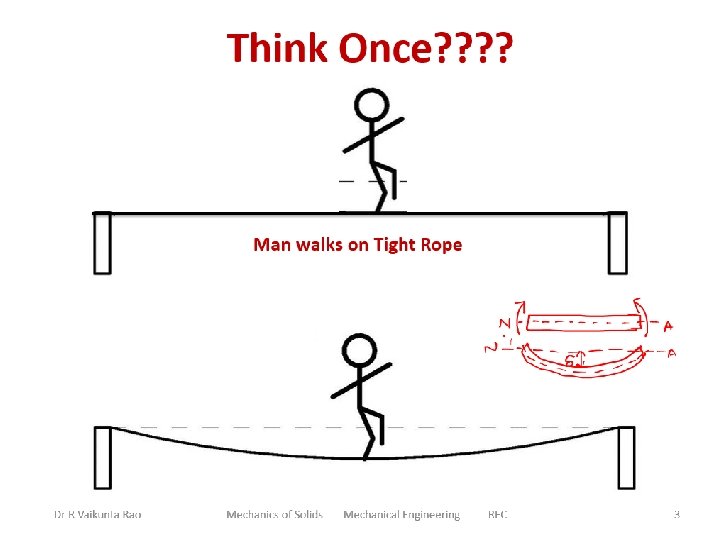
Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 3

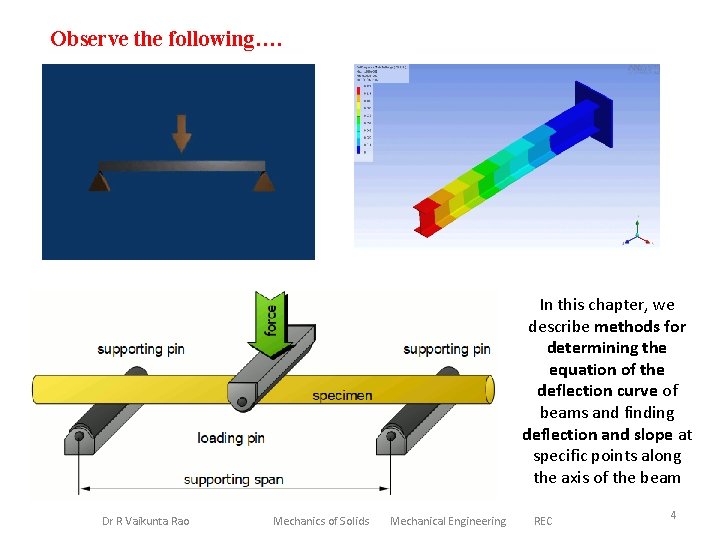
Observe the following…. In this chapter, we describe methods for determining the equation of the deflection curve of beams and finding deflection and slope at specific points along the axis of the beam Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 4

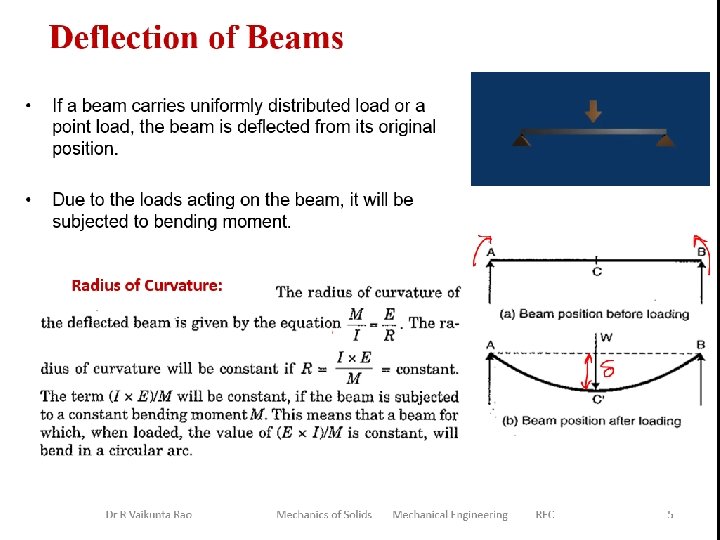
Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 5

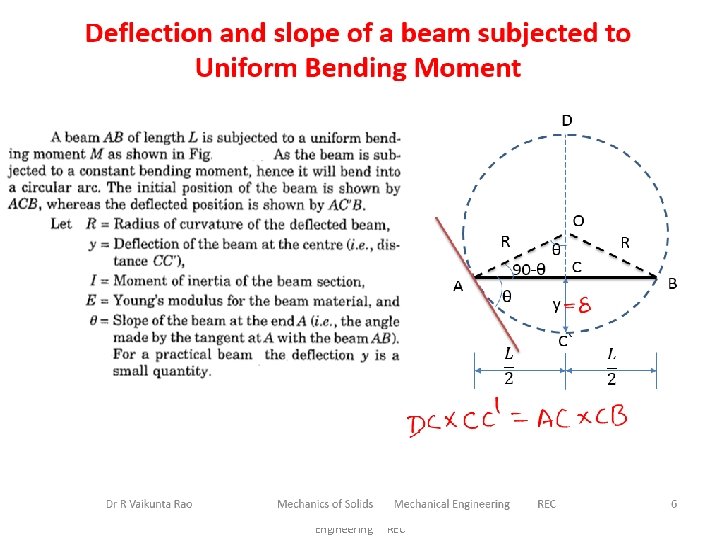
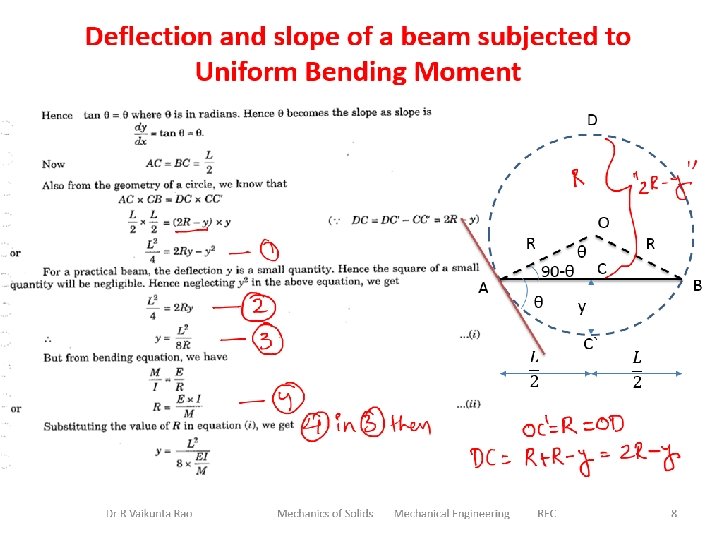
Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 6

Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 7

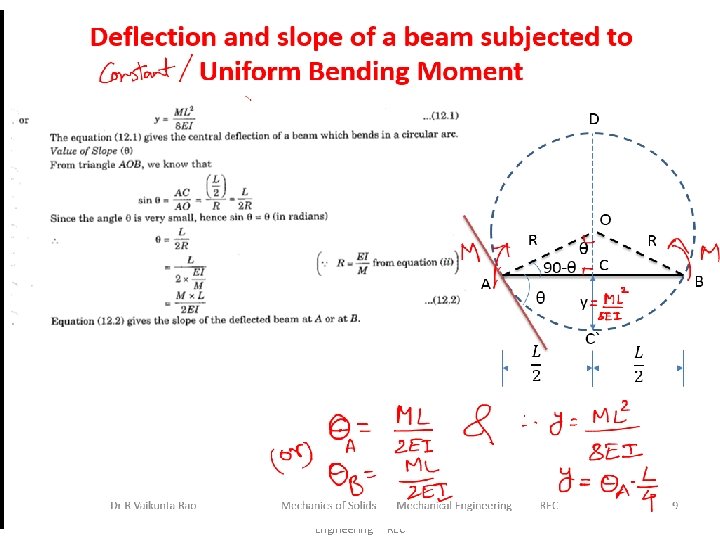
Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 8

Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 9

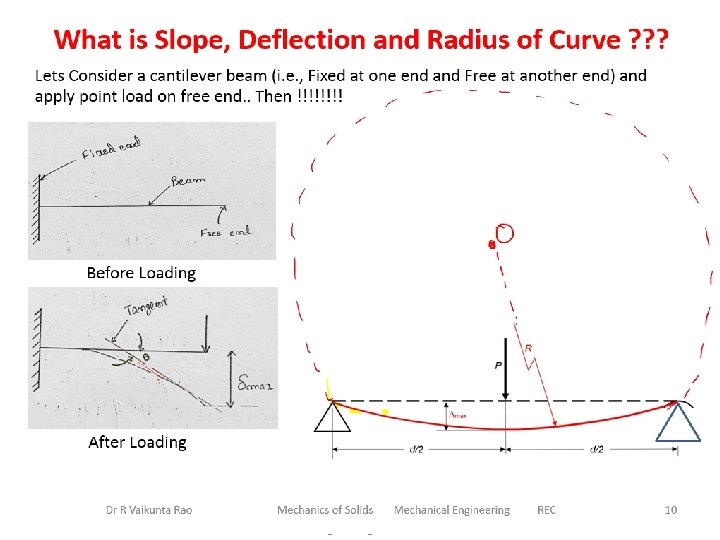
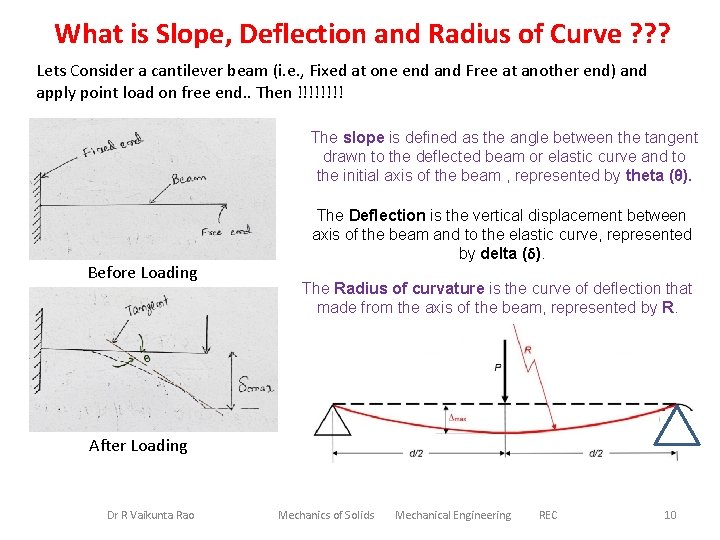
What is Slope, Deflection and Radius of Curve ? ? ? Lets Consider a cantilever beam (i. e. , Fixed at one end and Free at another end) and apply point load on free end. . Then !!!! The slope is defined as the angle between the tangent drawn to the deflected beam or elastic curve and to the initial axis of the beam , represented by theta (θ). Before Loading The Deflection is the vertical displacement between axis of the beam and to the elastic curve, represented by delta (δ). The Radius of curvature is the curve of deflection that made from the axis of the beam, represented by R. After Loading Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 10

Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 11

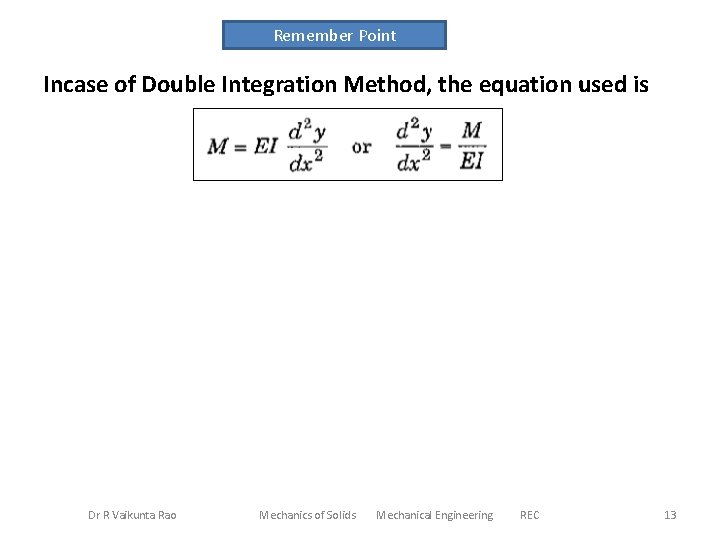
Methods of Representation Methods of Determining Slope and Deflection at a Section in a Loaded Beam 1. Double Integration Method 2. Moment Area Method 3. Macaulay’s Method Used for Single Load Used for Several Loads Incase of Double Integration Method, the equation used is Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 12

Remember Point Incase of Double Integration Method, the equation used is Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 13

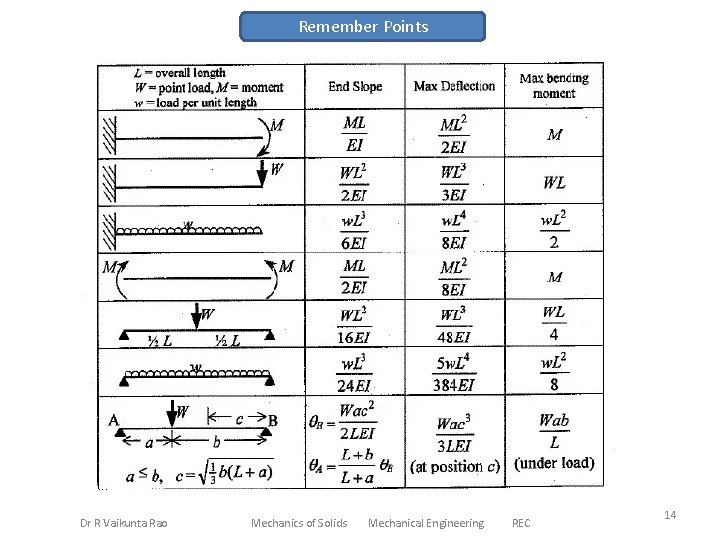
Remember Points Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 14

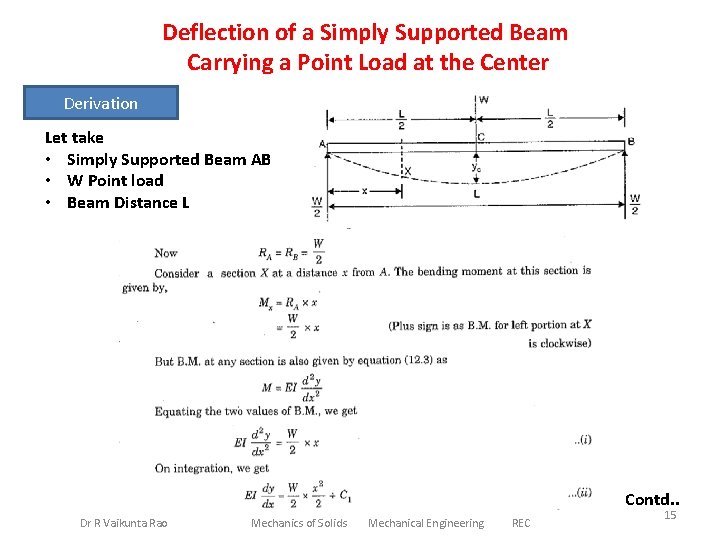
Deflection of a Simply Supported Beam Carrying a Point Load at the Center Derivation Let take • Simply Supported Beam AB • W Point load • Beam Distance L Contd. . Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 15

Deflection of a Simply Supported Beam Carrying a Point Load at the Center Contd. . Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 16

Deflection of a Simply Supported Beam Carrying a Point Load at the Center Contd. . Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 17

Deflection of a Simply Supported Beam Carrying a Point Load at the Center Finish. . Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 18

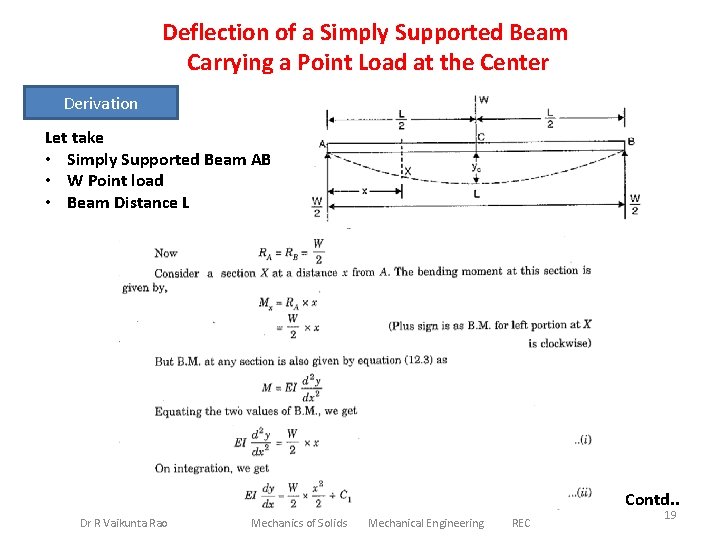
Deflection of a Simply Supported Beam Carrying a Point Load at the Center Derivation Let take • Simply Supported Beam AB • W Point load • Beam Distance L Contd. . Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 19

Deflection of a Simply Supported Beam Carrying a Point Load at the Center Contd. . Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 20

Deflection of a Simply Supported Beam Carrying a Point Load at the Center Contd. . Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 21

Deflection of a Simply Supported Beam Carrying a Point Load at the Center Finish. . Dr R Vaikunta Rao Mechanics of Solids Mechanical Engineering REC 22