Radius Ratio Rule In an ionic structure each

In an ionic structure each cation tends to surround itself with anions; the number

When this number is small, then only a few anions can fit around a

Radius Ratio Arrange of Anions around the cation Coordination Number (CN) 0. 15 -

Radius ratio Coordinate number Holes in which positive ions pack 0. 225 – 0.

IONIC CRYSTAL TYPES Ionic crystal type Co-ordination number A X Structure type AX 6

By using the calculations of radius ratio we can predict the coordination number. Example

By the same method we can predict that Na+ ions will prefer the octahedral

In this case there is two types of calculations : 1. rcation / ranion

Example : Rb 2 O r. Rb+ / r. O 2 - = 148

This radius ratio rule allows to predict the correct coordination no. of ions in

2. Li. I, Li. Br and Li. Cl have radius ratio less than 0.

As the size of positive ion decreases as the negativity of lattice energy increases

Predicting of Structure of complex of ionic compounds

This part is dealing with the structure of complex ionic compounds Here we are

Slides: 30

Download presentation

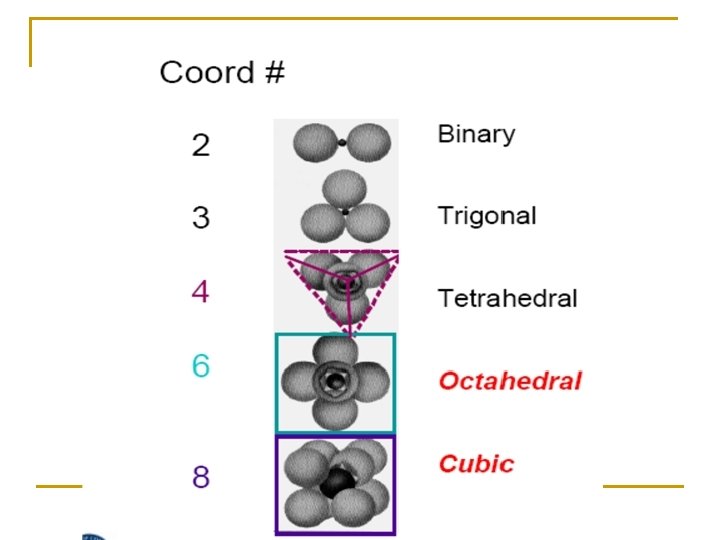
Radius Ratio Rule

In an ionic structure each cation tends to surround itself with anions; the number that can be grouped around it will depend on the relative size of the cations and anions. The Coordination Number (CN) is defined as the number of anions that can fit around a cation. This number increases as the radius ratio increases. The number of anions that can ‘fit’ around a cation is related to the relative size difference between the ions, and this size difference can be described using the radius ratio, which is given by: r cation /r anion

When this number is small, then only a few anions can fit around a cation. When this number is large, then more anions can fit around a cation. When CN is 4, it is known as tetrahedral coordination; when it is 6, it is octahedral; and when it is 8, it is known as cubic coordination. See the following table.

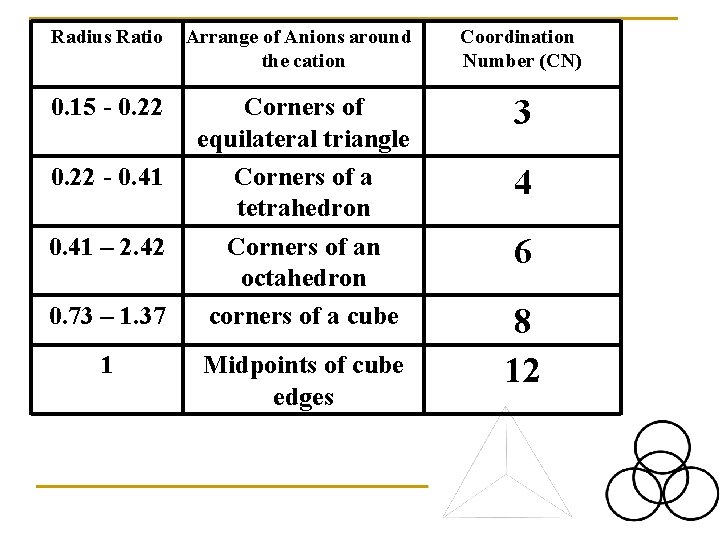
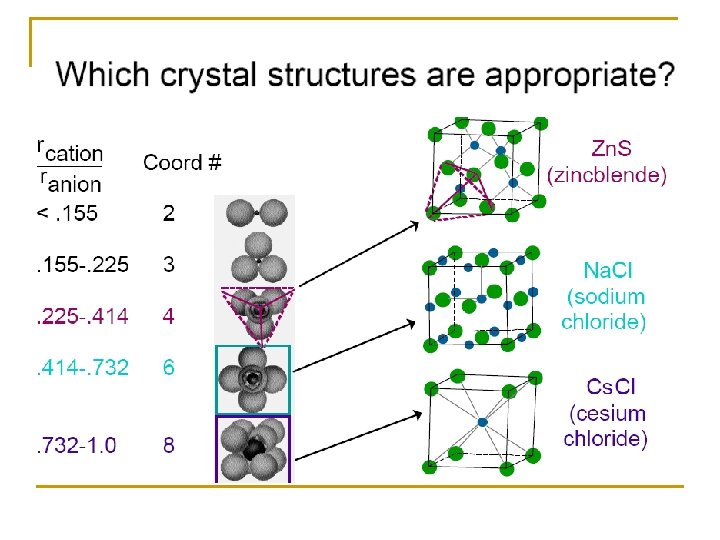
Radius Ratio Arrange of Anions around the cation Coordination Number (CN) 0. 15 - 0. 22 Corners of equilateral triangle Corners of a tetrahedron Corners of an octahedron corners of a cube 3 0. 22 - 0. 41 – 2. 42 0. 73 – 1. 37 1 Midpoints of cube edges 4 6 8 12

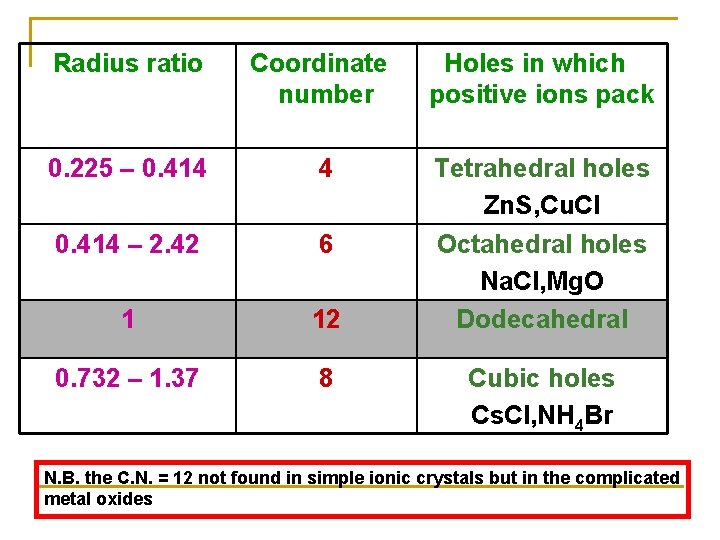
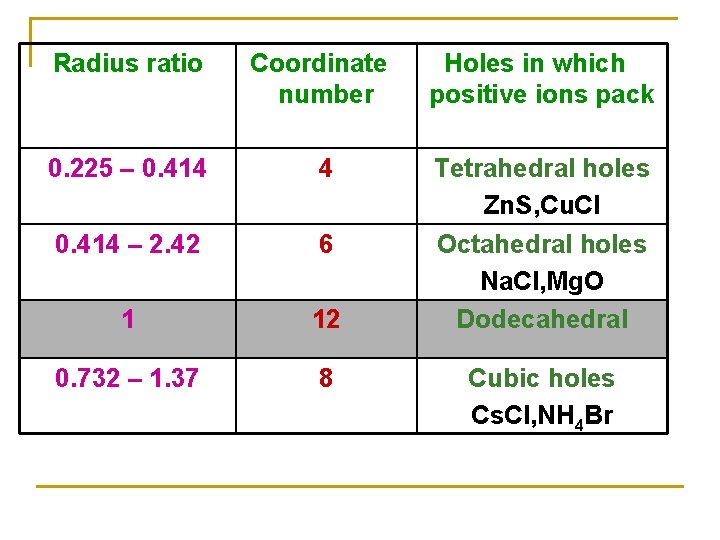
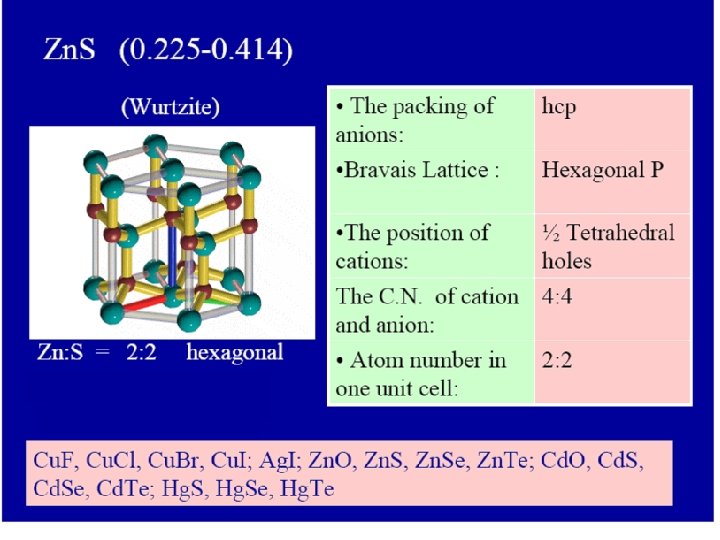
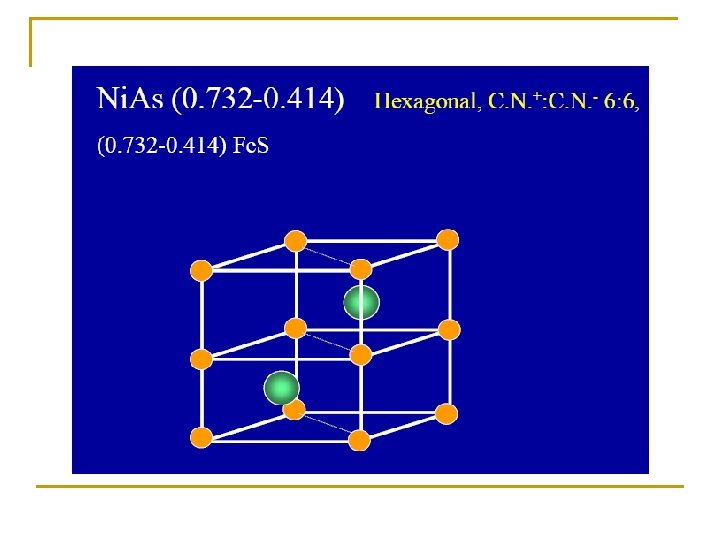
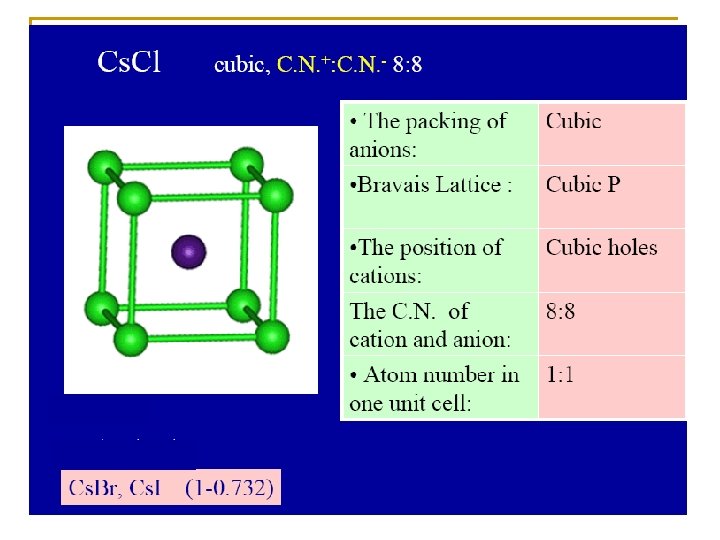
Radius ratio Coordinate number Holes in which positive ions pack 0. 225 – 0. 414 4 0. 414 – 2. 42 6 1 12 Tetrahedral holes Zn. S, Cu. Cl Octahedral holes Na. Cl, Mg. O Dodecahedral 0. 732 – 1. 37 8 Cubic holes Cs. Cl, NH 4 Br N. B. the C. N. = 12 not found in simple ionic crystals but in the complicated metal oxides

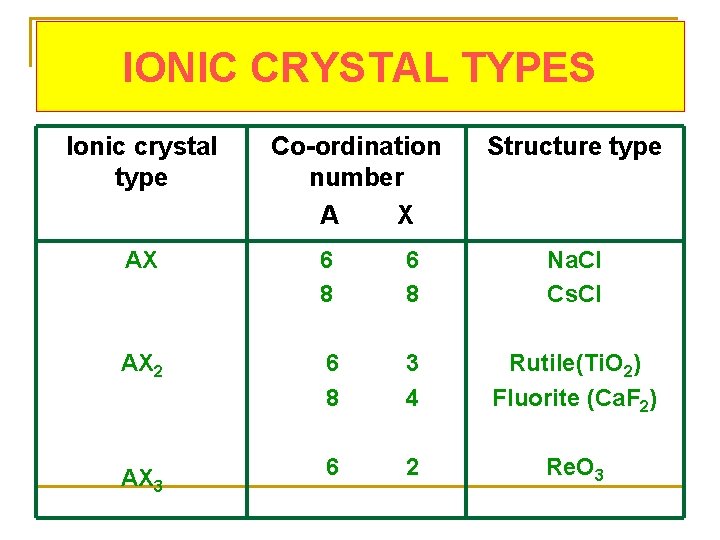
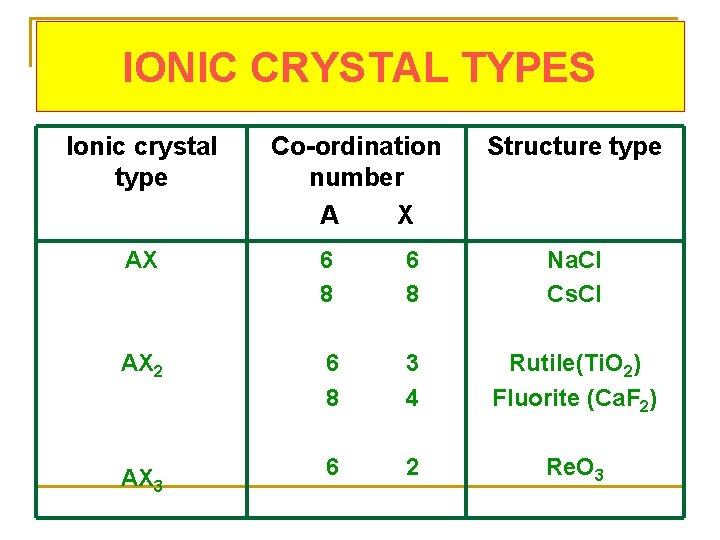
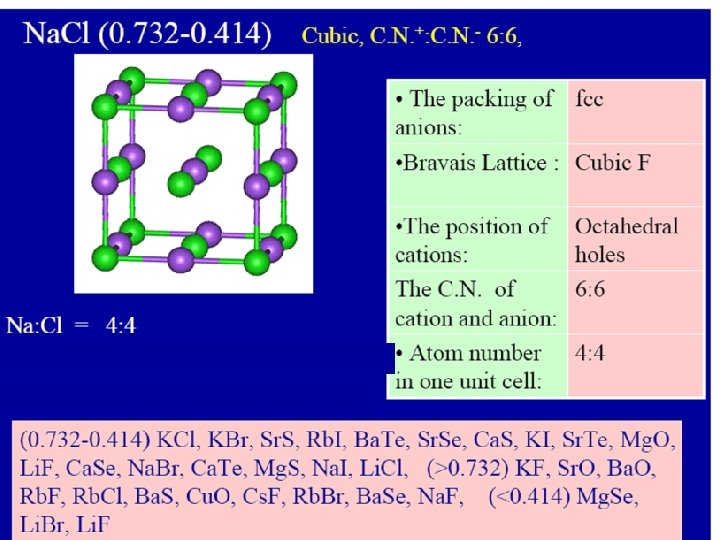
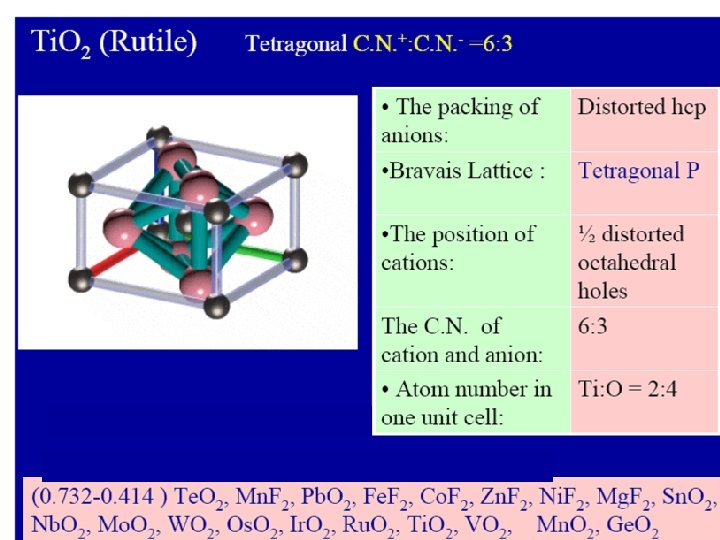
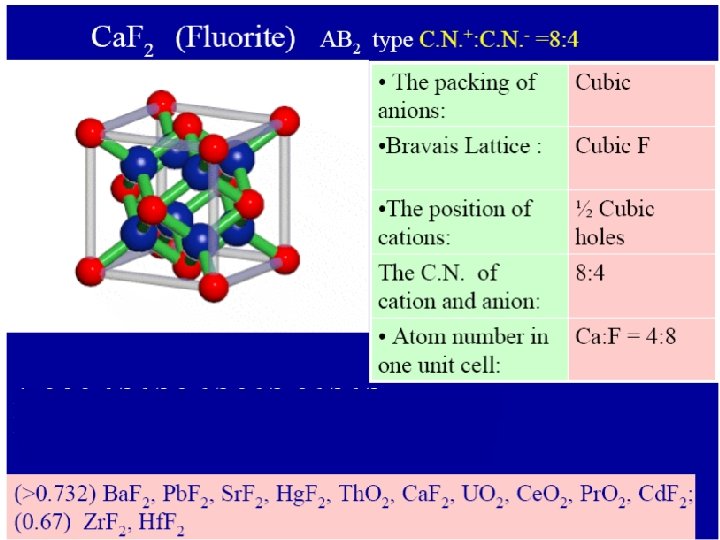
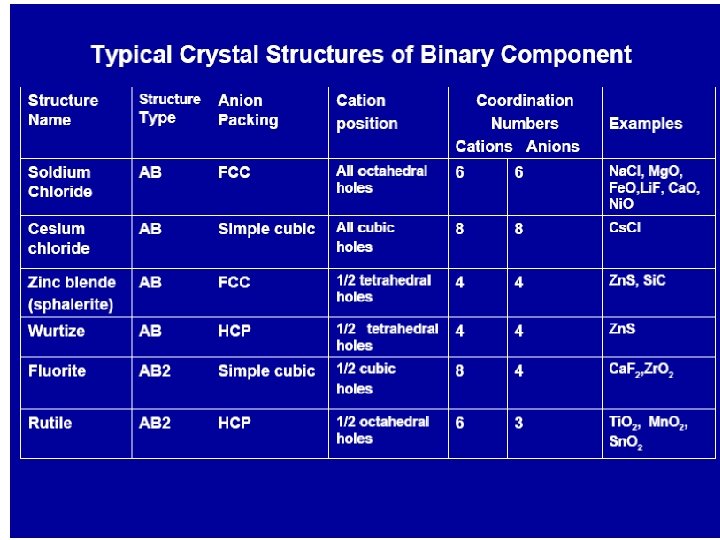
IONIC CRYSTAL TYPES Ionic crystal type Co-ordination number A X Structure type AX 6 8 Na. Cl Cs. Cl AX 2 6 8 3 4 Rutile(Ti. O 2) Fluorite (Ca. F 2) AX 3 6 2 Re. O 3

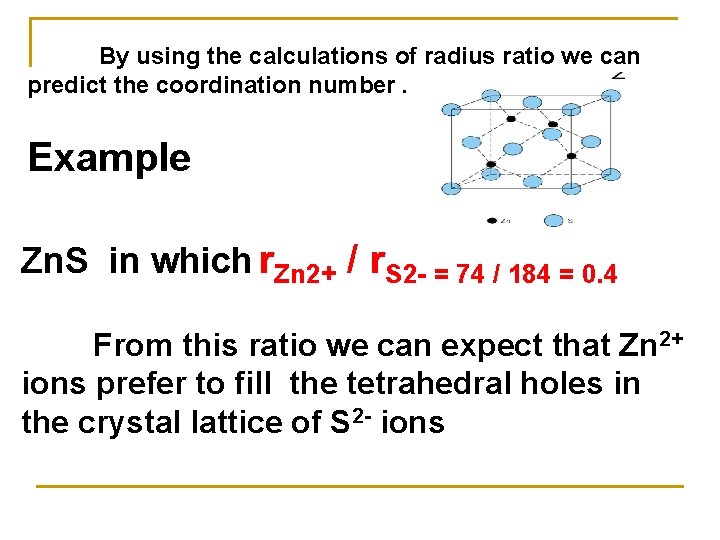
By using the calculations of radius ratio we can predict the coordination number. Example Zn. S in which r. Zn 2+ / r. S 2 - = 74 / 184 = 0. 4 From this ratio we can expect that Zn 2+ ions prefer to fill the tetrahedral holes in the crystal lattice of S 2 - ions

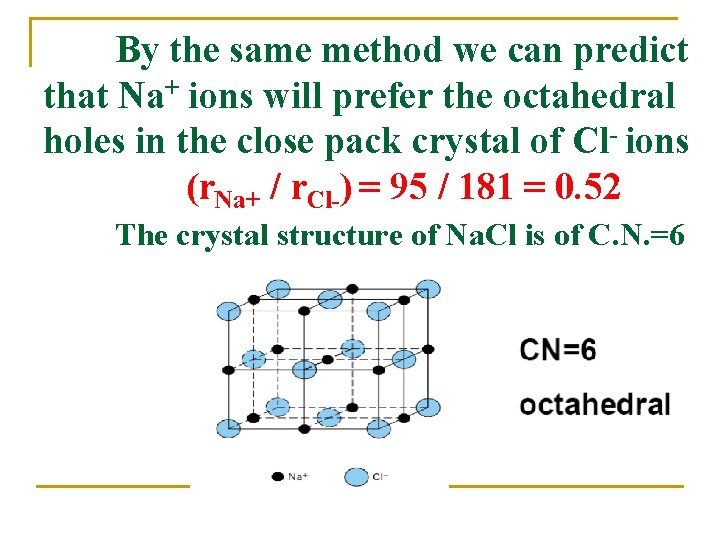
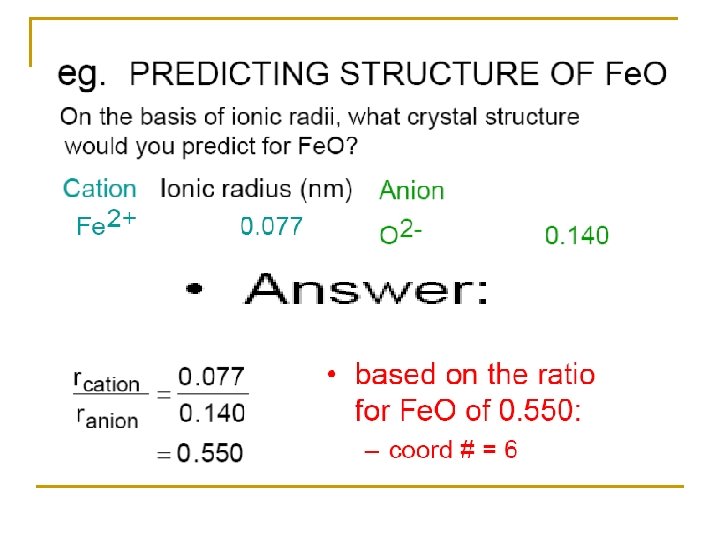
By the same method we can predict that Na+ ions will prefer the octahedral holes in the close pack crystal of Cl- ions (r. Na+ / r. Cl-) = 95 / 181 = 0. 52 The crystal structure of Na. Cl is of C. N. =6

IONIC CRYSTAL TYPES Ionic crystal type Co-ordination number A X Structure type AX 6 8 Na. Cl Cs. Cl AX 2 6 8 3 4 Rutile(Ti. O 2) Fluorite (Ca. F 2) AX 3 6 2 Re. O 3

In this case there is two types of calculations : 1. rcation / ranion 2. ranion / rcation e. g. Ca. F 2 C. N. =8 1 C. N. =8 ranion / rcation = 0. 133 / 0. 1= 1. 33 2 But the no. of F- ions must be twice of Ca 2+ so the C. N. of Ca 2+ ions twice that of F- ions so C. N. of Ca 2+ = 8 and C. N. of F- = 4

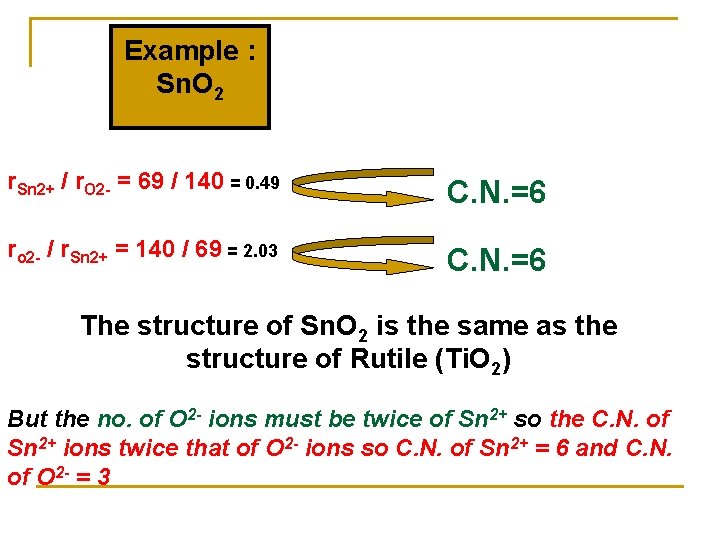
Example : Sn. O 2 r. Sn 2+ / r. O 2 - = 69 / 140 = 0. 49 C. N. =6 ro 2 - / r. Sn 2+ = 140 / 69 = 2. 03 C. N. =6 The structure of Sn. O 2 is the same as the structure of Rutile (Ti. O 2) But the no. of O 2 - ions must be twice of Sn 2+ so the C. N. of Sn 2+ ions twice that of O 2 - ions so C. N. of Sn 2+ = 6 and C. N. of O 2 - = 3

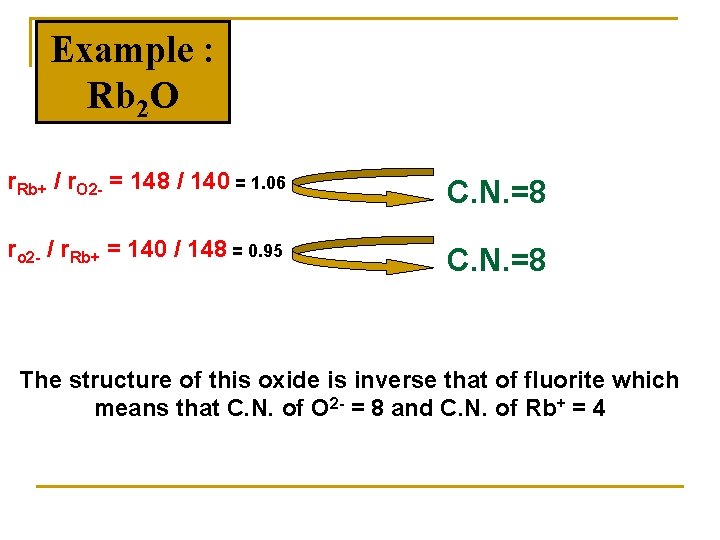
Example : Rb 2 O r. Rb+ / r. O 2 - = 148 / 140 = 1. 06 C. N. =8 ro 2 - / r. Rb+ = 140 / 148 = 0. 95 C. N. =8 The structure of this oxide is inverse that of fluorite which means that C. N. of O 2 - = 8 and C. N. of Rb+ = 4

Exceptions

This radius ratio rule allows to predict the correct coordination no. of ions in the crystal lattice. BUT 1. This rule must be used under precautions , specially in covalent bonding , e. g. Cd. S , we can find the radius ratio = 0. 53 which leads to C. N. =6 Although the structure of this compound is like the structure of Zn. S in which C. N. =4. This means that the covalent bonding between Cd and S prefer C. N. =4

2. Li. I, Li. Br and Li. Cl have radius ratio less than 0. 414 although all of them have the Na. Cl structure. Covalent Bonding Not pure Ionic Bonding less than 100% ionic bonding 3. The alkali metals of covalent bonding.

As the size of positive ion decreases as the negativity of lattice energy increases which mean more stability in crystal lattice. Ex. Zn. S which has the zinc Blende structure in which Zn. S has lattice energy more than that if take any crystal structure else

Predicting of Structure of complex of ionic compounds

This part is dealing with the structure of complex ionic compounds Here we are dealing with two types of complex ionic compounds : 1. Compounds of general formula A 2 BO 4 , since A is the metal and B is another metal of higher valence than A or could be nonmetal. Spinel Structure

2. Perovskite structure AB 2 O 3