Radiometry Outline l l What is Radiometry Quantities

Radiometry

Outline l l What is Radiometry? Quantities l l Radiant energy, flux density Irradiance, Radiance Spherical coordinates, foreshortening Modeling surface properties: the BRDF l l Lambertian Specular

Radiometry l Geometry of perspective projection explains location of scene point in image, but what about its intensity and color? l Radiometry is the measurement of electromagnetic radiation, primarily optical l l Frequencies from infrared to visible to ultraviolet Photometry quantifies camera/eye sensitivity

Measuring Light l l For now, ignore the fact that light has multiple wavelengths; we’ll come back to this when we discuss color Fundamental quantities l l l Radiant energy Q (measured in joules J) l Proportional to number of photons (and photon frequency) Radiant flux/power © of a light source (watts W) l Joules per second emitted Radiant flux density (Wm 2) l Power per unit area through a surface (real or imaginary) from all directions

Incoming and Outgoing Light at a Surface l Irradiance E (Wm 2) Light arriving at a point on a surface from all visible directions l An image samples the irradiance at the pinhole 2 l Radiosity B (Wm ) l Light leaving a surface in all directions l

Radiance l Radiance L (Wm 2 sr 1) l l l Power at a point in space in a given direction, foreshortened Can be incoming or outgoing Does not attenuate with distance in vacuum What is stored in a pixel—the light energy arriving along a particular ray at a particular point. The more the surface is tilted away, the larger an area the light energy is distributed over.

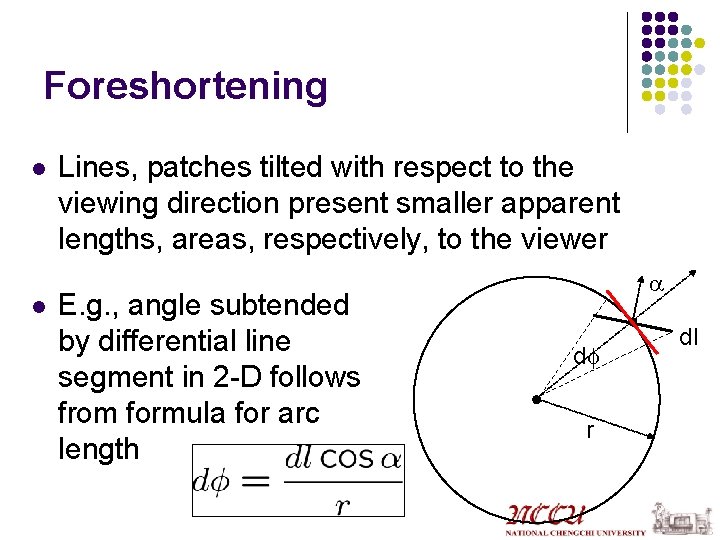
Foreshortening l l Lines, patches tilted with respect to the viewing direction present smaller apparent lengths, areas, respectively, to the viewer E. g. , angle subtended by differential line segment in 2 D follows from formula for arc length a df r dl

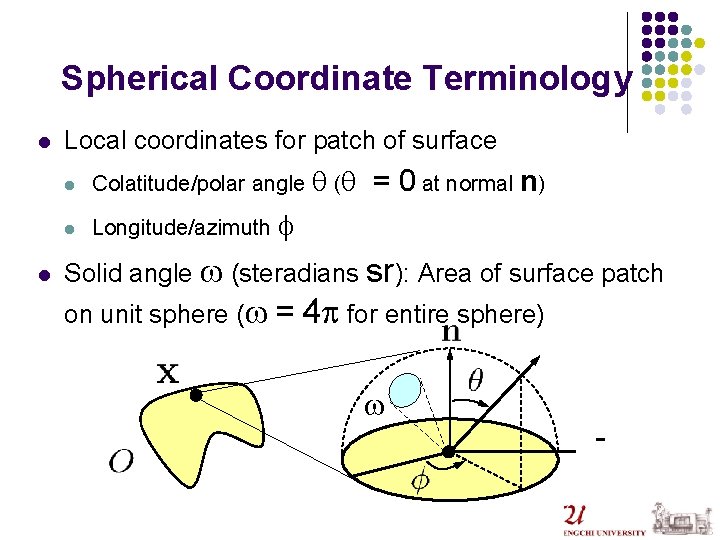
Spherical Coordinate Terminology l l Local coordinates for patch of surface l Colatitude/polar angle q (q l Longitude/azimuth f = 0 at normal n) Solid angle w (steradians sr): Area of surface patch on unit sphere (w = 4 p for entire sphere) w

3 -D Foreshortening l For patches, just extend 2 D argument to areas: l Foreshortening factor for light coming from (q, f) is just cosq

Solid Angle in Spherical Coordinates l Differential patch dqdf has smaller area closer to pole due to shrinking width of df l Circumference at a given polar angle q is 2 prsinq, so the correct patch area is dw = sinqdqdf in q rs r

Computing Irradiance l Integrate radiance over the hemisphere l Thus, irradiance from a particular direction is

Describing an Environment’s Radiance l Radiance distribution l l 5 dimensional function (3 position + 2 direction variables) Environment map: Radiance distribution at a given point Plenoptic function: Time variable added Light field l l Radiance distribution for an object 4 dimensional function: All positions on image planes of all orthographic views of object

BRDF l Bidirectional Reflectance Distribution Function (BRDF): Ratio of outgoing radiance in one direction to incident irradiance

BRDF Properties l l l Energy leaving · energy arriving Symmetric in both directions (Helmholtz reciprocity) Generally, only difference between incident and emitted angle f is significant l l Dependence on absolute f Anisotropy Can view BRDF as probability that incoming photon will leave in a particular direction courtesy of S. Rusinkiewicz

Things the BRDF neglects l l Surface non uniformity Subsurface scattering l l Light moving under the surface and emerging elsewhere—e. g. , marble, skin BRDF Transmission l Light going through to other side BSSRDF courtesy of H. Jensen

Reflectance Equation l Radiance for a viewing direction given all incoming light l This is proportional to the pixel brightness for that ray

Lambertian Surfaces l Diffuse/matte reflectance: Radiance leaving surface does not depend on angle l Albedo r: Ratio of light reflected by an object to light received l BRDF: f(. ) =r/p

Specular Surfaces l l l Mirrorlike: Radiance only leaves along specular direction (reflection of incoming direction) BRDF: Specular lobe models shiny that is not perfect mirror surface