Radioactivity 2 Decay Chains and Equilibrium IAEA International

Radioactivity -2 Decay Chains and Equilibrium IAEA International Atomic Energy Agency Day 1 – Lecture 5

Objective To discuss radioactive decay chains (parent and single decay product) and equilibrium situations IAEA 2

Content Ø Secular equilibrium Ø Transient equilibrium Ø Case of no equilibrium Ø Radioactive decay series Ø Ingrowth of decay product from a parent radionuclide IAEA 3

Types of Radioactive Equilibrium Secular IAEA Half-life of parent much greater (> 100 times) than that of decay product 4

Types of Radioactive Equilibrium Transient IAEA Half-life of parent only greater (only 10 times greater) than that of decay product 5

Sample Radioactive Series Decay 90 Sr 90 Y 90 Zr where 90 Sr is the parent (half-life = 28 years) and 90 Y is the decay product (half-life = 64 hours) IAEA 6

Differential Equation for Radioactive Series Decay Parent and Single Decay Product d. NY = Sr NSr - Y NY dt IAEA The instantaneous rate of change of Y-90 is made up of two terms: the production rate, which is equal to the Sr-90 decay rate; and the rate of loss, which is the decay rate of Y-90.

Differential Equation for Radioactive Series Decay Parent and Single Decay Product Sr. NSr t t Sr (e - e Y) NY(t) = Y - Sr o Recall that Sr No. Sr = Ao. Sr which equals the initial activity of 90 Sr at time t = 0 IAEA

General Equation for Radioactive Series Decay Activity of 90 Sr at time t = 0 Y Sr. NSr - Srt - t. Y (e -e ) YNY(t) = Y - Sr o Activity of 90 Y at time t or AY(t) IAEA

Secular Equilibrium Buildup of a Decay Product under Secular Equilibrium Conditions AY(t) = ASr (1 - e- Yt) IAEA 10

Secular Equilibrium Sr. NSr = YNY ASr = AY At secular equilibrium the activities of the parent and decay product are equal and constant with time IAEA 11

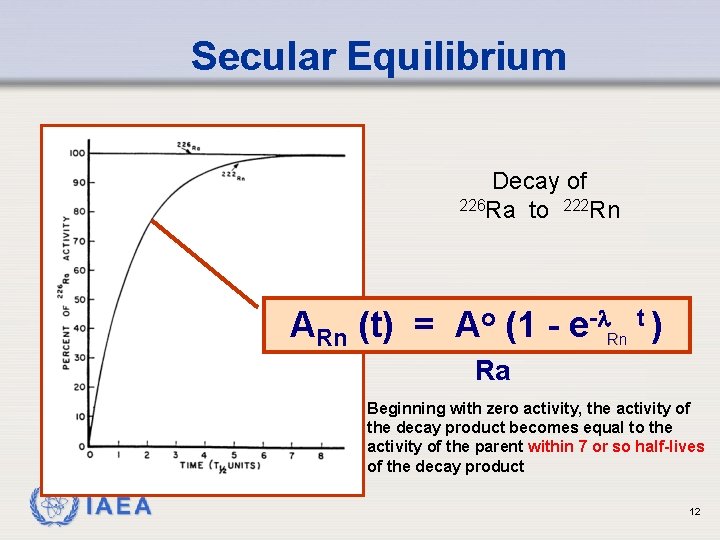
Secular Equilibrium Decay of 226 Ra to 222 Rn ARn (t) = Ao (1 - e- Rn t ) Ra Beginning with zero activity, the activity of the decay product becomes equal to the activity of the parent within 7 or so half-lives of the decay product IAEA 12

Sample Problem 1 226 Ra (half-life 1600 years) decays to 222 Rn (halflife 3. 8 days). If initially there is 100 µCi of 226 Ra in a sample and no 222 Rn, calculate how much 222 Rn is produced: a. b. after 7 half-lives of 222 Rn at equilibrium IAEA

Solution to Sample Problem The number of atoms of 222 Rn at time t is given by: d. NRn dt = Ra NRa - Rn NRn Solving: NRn(t) = IAEA Ra. NRa Rn (1 - e- Rnt)

Solution to Sample Problem Multiplying both sides of the equation by Rn: ARn(t) = ARa (1 - e- Rn t) Let t = 7 TRn Rnt = (0. 693/TRn) x 7 TRn = 0. 693 * 7 = 4. 85 e-4. 85 = 0. 00784 ARn (7 half-lives) = 100 µCi * (1 - 0. 00784 ) = 100 * (0. 992) = 99. 2 µCi of 222 Rn IAEA

Solution to Sample Problem Now, at secular equilibrium: Rn. NRn = Ra. NRa or ARn = ARa = 100 µCi Note that the total activity in this sample is: Rn. NRn + Ra. NRa or ARn + ARa = 100 µCi + 100 µCi = 200 µCi IAEA

Transient Equilibrium D P NP DN D = D - P For the case of transient equilibrium, the general equation for radioactive series decay reduces to the above equation. IAEA

Transient Equilibrium AD = IAEA AP D D - P Expressing it in terms of activities of parent and decay product.

Transient Equilibrium Time for Decay Product to Reach Maximum Activity tm. D IAEA D ln P = D - P

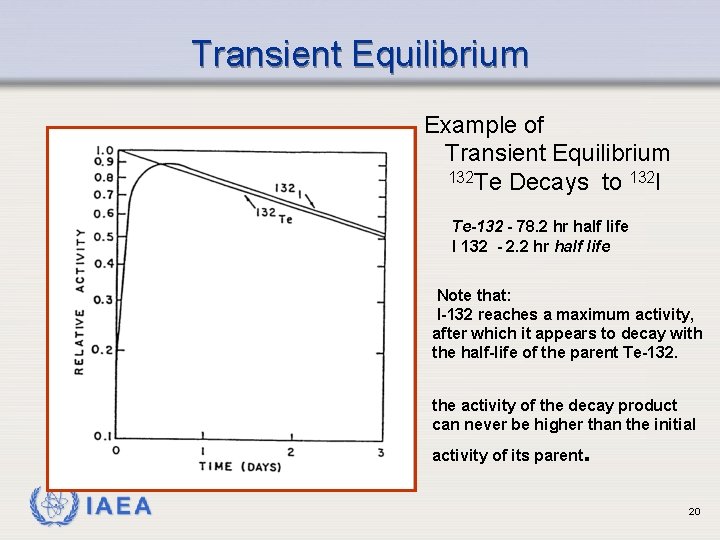
Transient Equilibrium Example of Transient Equilibrium 132 Te Decays to 132 I Te-132 - 78. 2 hr half life I 132 - 2. 2 hr half life Note that: I-132 reaches a maximum activity, after which it appears to decay with the half-life of the parent Te-132. the activity of the decay product can never be higher than the initial activity of its parent IAEA . 20

Sample Problem The principle of transient equilibrium is illustrated by the Molybdenum-Technetium radioisotope generator used in nuclear medicine applications. Given initially that the generator contains 100 m. Ci of 99 Mo (half-life 66 hours) and no 99 m. Tc (half-life 6 hours) calculate the: a. time required for 99 m. Tc to reach its maximum activity b. activity of 99 Mo at this time, and c. activity of 99 m. Tc at this time IAEA

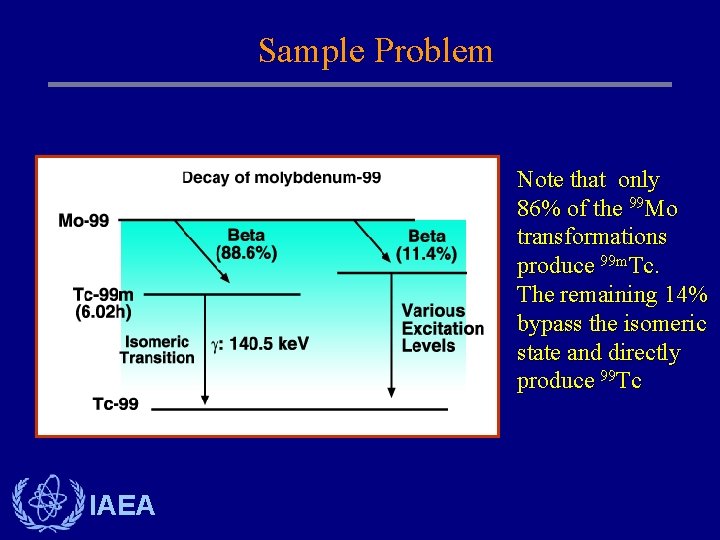
Sample Problem Note that only 86% of the 99 Mo transformations produce 99 m. Tc. The remaining 14% bypass the isomeric state and directly produce 99 Tc IAEA

Solution to Sample Problem ln a) tm. Tc = Tc Mo Tc - Mo Tc = 0. 693/(6 hr) = 0. 12 hr-1 Mo = 0. 693/(66 hr) = 0. 011 hr-1 ln tm. Tc = IAEA 0. 12 0. 011 0. 12 – 0. 011 = 21. 9 hrs

Solution to Sample Problem (b) The activity of 99 Mo is given by A(t) = Ao e- t = 100 m. Ci e(-0. 011/hr * 21. 9 hr) = 100 * (0. 79) = 79 m. Ci IAEA

Solution to Sample Problem c) The activity of 99 m. Tc at t = 21. 9 hrs is given by: Tc. AMo t) ATc(t) = (e- Mot - e- Tc Tc - Mo ATc(t) = (0. 12)(100 m. Ci)(0. 86) (0. 12 – 0. 011) (see slide 10) (e-(0. 011)(21. 9) - e-(0. 12)(21. 9)) = (94. 7) (0. 785 - 0. 071) = 67. 6 m. Ci of 99 m. Tc IAEA

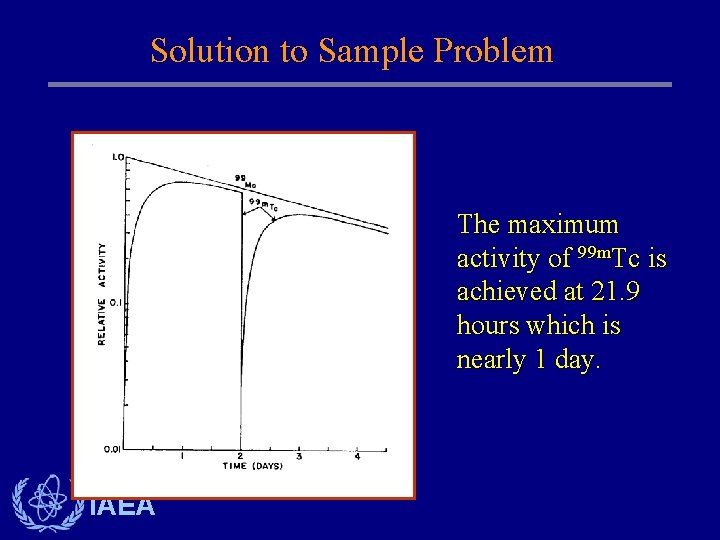
Solution to Sample Problem The maximum activity of 99 m. Tc is achieved at 21. 9 hours which is nearly 1 day. IAEA

Types of Radioactive Equilibrium No Equilibrium IAEA Half-life of parent less than that of decay product 27

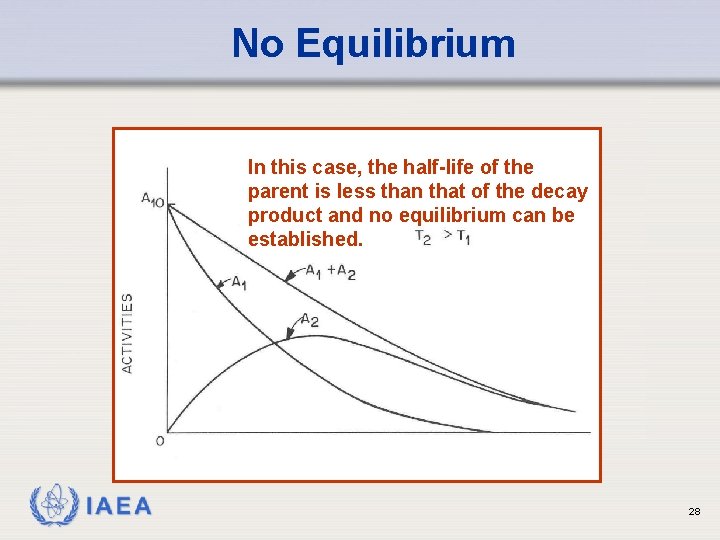
No Equilibrium In this case, the half-life of the parent is less than that of the decay product and no equilibrium can be established. IAEA 28

Summary Ø Activity defined and units discussed Ø Decay constant defined Ø Half-life defined - relationship to decay constant Ø Radioactive decay equation derived Ø Mean life derived - relationship to half-life Ø Secular equilibrium was defined Ø Transient equilibrium was defined Ø Case of no equilibrium was defined IAEA 29

Where to Get More Information Ø Cember, H. , Johnson, T. E, Introduction to Health Physics, 4 th Edition, Mc. Graw-Hill, New York (2009) Ø International Atomic Energy Agency, Postgraduate Educational Course in Radiation Protection and the Safety of Radiation Sources (PGEC), Training Course Series 18, IAEA, Vienna (2002) IAEA 30