Radioactivit 2 Chaines de dcroissance radioactive et Equilibre

Radioactivité -2 Chaines de décroissance radioactive et Equilibre IAEA International Atomic Energy Agency Jour 1 – Presentation 5

Objectif Discuter les chaines de décroissance radioactive (le père et le produit unique de désintégration) et les situations d’équilibre IAEA 2

Contenu Ø Equilibre Séculaire Ø Equilibre transitoire Ø Cas de non-équilibre Ø Séries de décroissance radioactive Ø Croissance d'un produit de désintégration à partir d'un radionucléide père IAEA 3

Types d’équilibres Radioactifs Séculaire La demi-vie du père est beaucoup plus grande (> 100 fois) que celle de produit de désintégration (fils) T 1/2 père >>>T 1/2 fils IAEA 4

Types d’équilibres Radioactifs Transitoire La demi-vie du père est seulement 10 fois plus grande que celle du produit de désintégration T 1/2 père ~ 10 T 1/2 fils IAEA 5

Exemple de séries de désintégration Radioactive 90 Sr 90 Y 90 Zr où 90 Sr est le père (demi-vie = 28 ans) et 90 Y est le produit de décroissance (demi-vie = 64 heures) IAEA 6

Equation Différentielle pour les Séries de décroissance radioactive Le père et le produit unique de décroissance d. NY = Sr NSr - Y NY dt IAEA Le taux instantané de variation de Y-90 est composé de deux termes: le taux de production, qui est égale à la vitesse de décroissance du Sr-90; et le taux de perte, ce qui est le taux de décroissance de Y-90.

Equation Différentielle pour les Séries de décroissance radioactive Le père et le produit unique de désintégration Sr. NSr t t Sr (e - e Y) NY(t) = Y - Sr o Rappelons que Sr No. Sr = Ao. Sr qui est égal à l’activité initiale du 90 Sr au temps t = 0 IAEA

Equation Générale pour Les séries de décroissance radioactive Activité du 90 Sr au temps t = 0 Y Sr. NSr - Srt - t. Y (e -e ) YNY(t) = Y - Sr o Activité du 90 Y au temps t ou AY(t) IAEA

Equilibre Séculaire Les Conditions d'accumulation d'un produit de décroissance dans les conditions d'équilibre séculaire AY(t) = ASr (1 - e- Yt) IAEA 10

Equilibre Séculaire Sr. NSr = YNY ASr = AY A l’équilibre séculaire, l’activité du père et celle du fils sont égales et constantes dans le temps IAEA 11
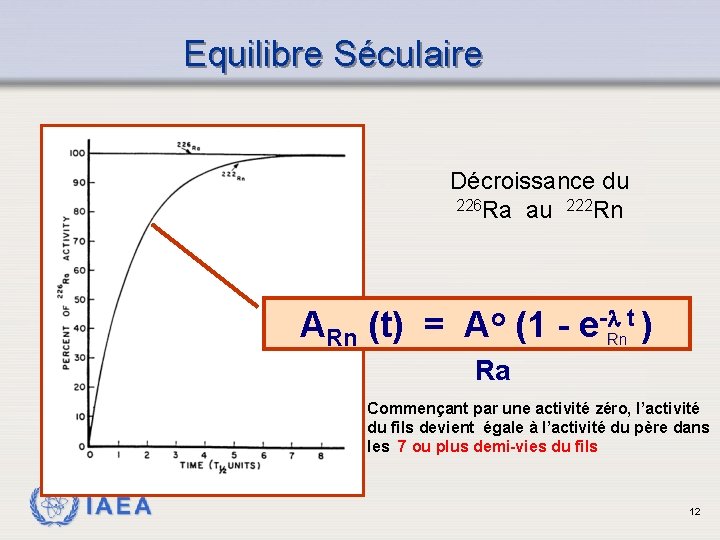
Equilibre Séculaire Décroissance du 226 Ra au 222 Rn ARn (t) = Ao (1 - e- Rnt ) Ra Commençant par une activité zéro, l’activité du fils devient égale à l’activité du père dans les 7 ou plus demi-vies du fils IAEA 12

Exemple - Problème 1 226 Ra (demi-vie = 1600 ans) se désintègre pour donner le 222 Rn (demi-vie = 3. 8 jours). Si on a initialement 100 µCi du 226 Ra dans un échantillon et pas de 222 Rn, calculer l’activité produite du 222 Rn: a. Après 7 demi-vies du 222 Rn b. À l’équilibre Ce problème va illustrer l’équilibre séculaire IAEA

Solution du Problème Le nombre d’atome de 222 Rn au temps t est donné par: d. NRn dt = Ra NRa - Rn NRn Solution: NRn(t) = IAEA Ra. NRa Rn (1 - e- Rnt)

Solution du Problème Multiplions les deux membres de l’équation par Rn: ARn(t) = ARa (1 - e- Rn t) Si t = 7 TRn Rnt = (0. 693/TRn) x 7 TRn = 0. 693 * 7 = 4. 85 e-4. 85 = 0. 00784 ARn (7 demi-vies) = 100 µCi * (1 - 0. 00784 ) = 100 * (0. 992) = 99. 2 µCi du IAEA 222 Rn

Solution du Problème Maintenant à l’équilibre Séculaire: Rn. NRn = Ra. NRa ou ARn = ARa = 100 µCi Noter que l’activité totale dans ce cas est: Rn. NRn + Ra. NRa ou ARn + ARa = 100 µCi + 100 µCi = 200 µCi IAEA

Equilibre Transitoire fils Père NPère fils. Nfils = fils - Père Pour le cas de l'équilibre transitoire, l'équation générale pour une série de décroissances radioactives se réduit à l'équation ci-dessus IAEA

Equilibre Transitoire Afils = IAEA APère fils - Père Exprimant la en terme d’activités du père et celle du fils

Equilibre Transitoire Le temps max. pour avoir l’activité maximale du fils Tm fils IAEA fils ln Père = fils - Père
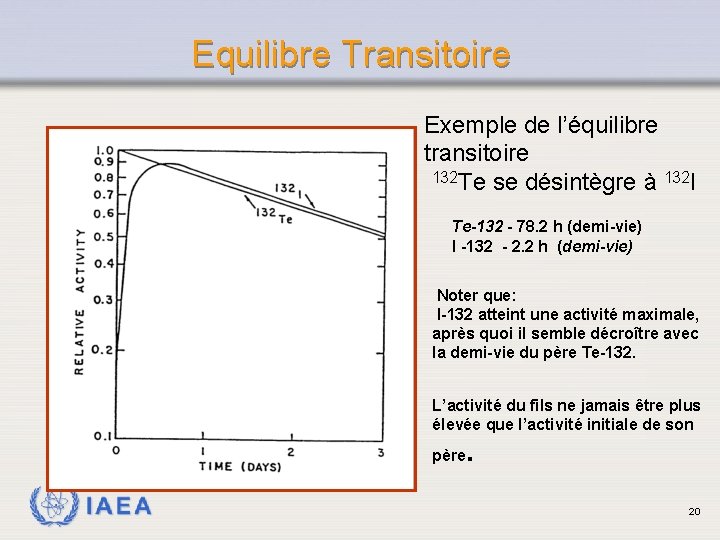
Equilibre Transitoire Exemple de l’équilibre transitoire 132 Te se désintègre à 132 I Te-132 - 78. 2 h (demi-vie) I -132 - 2. 2 h (demi-vie) Noter que: I-132 atteint une activité maximale, après quoi il semble décroître avec la demi-vie du père Te-132. L’activité du fils ne jamais être plus élevée que l’activité initiale de son père IAEA . 20

Exemple: Problème Le principe de l'équilibre transitoire est illustré par le générateur de molybdène-technétium, radio-isotopes utilisés dans des applications en médecine nucléaire. On considère initialement que le Générateur contient 100 m. Ci de 99 Mo (demi-vie 66 h) et pas de 99 m. Tc (demi-vie 6 h) calculer: a. Le temps nécessaire pour que le 99 m. Tc atteigne le maximum de son activité b. l’activité de 99 Mo à ce temps, et c. l’activité de 99 m. Tc à ce temps IAEA

Exemple: Problème Noter que seulement 86% transformations de 99 Mo produisent le 99 m. Tc. Le reste qui est 14% se transforme en 99 Tc qui n’est pas utilisable en médecine nucléaire. IAEA

Solution du Problème Tc Mo ln a) tm. Tc = Tc - Mo Tc = 0. 693/(6 h) = 0. 12 h-1 Mo = 0. 693/(66 h) = 0. 011 h-1 ln tm. Tc = IAEA 0. 12 0. 011 0. 12 – 0. 011 = 21. 9 h

Solution du Problème (b) l’activité de 99 Mo est donnée par: A(t) = Ao e- t = 100 m. Ci e(-0. 011/hr * 21. 9 hr) = 100 * (0. 79) = 79 m. Ci IAEA

Solution du Problème c) L’activité du 99 m. Tc à t = 21. 9 h est donnée par: Tc. AMo t) ATc(t) = (e- Mot - e- Tc Tc - Mo ATc(t) = (0. 12)(100 m. Ci)(0. 86) (0. 12 – 0. 011) (voir diapos 10) (e-(0. 011)(21. 9) - e-(0. 12)(21. 9)) = (94. 7) (0. 785 - 0. 071) = 67. 6 m. Ci du 99 m. Tc IAEA
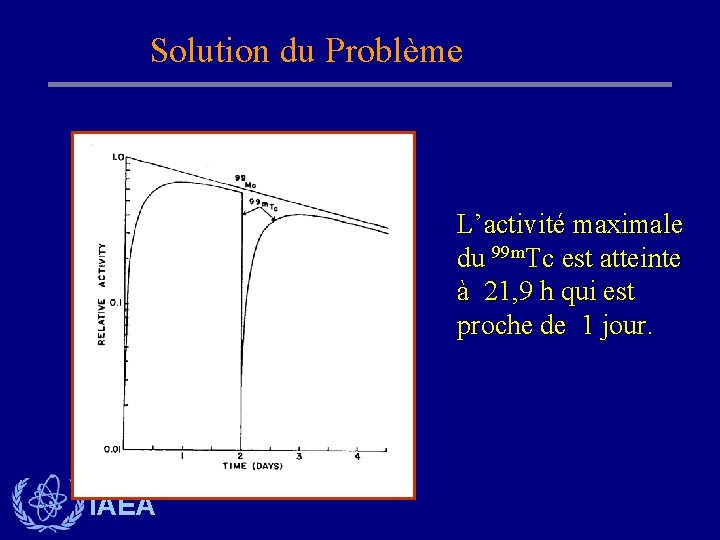
Solution du Problème L’activité maximale du 99 m. Tc est atteinte à 21, 9 h qui est proche de 1 jour. IAEA

Types d’équilibres radioactifs Pas d’équilibre IAEA La demi-vie du père est inférieure à celle du fils 27
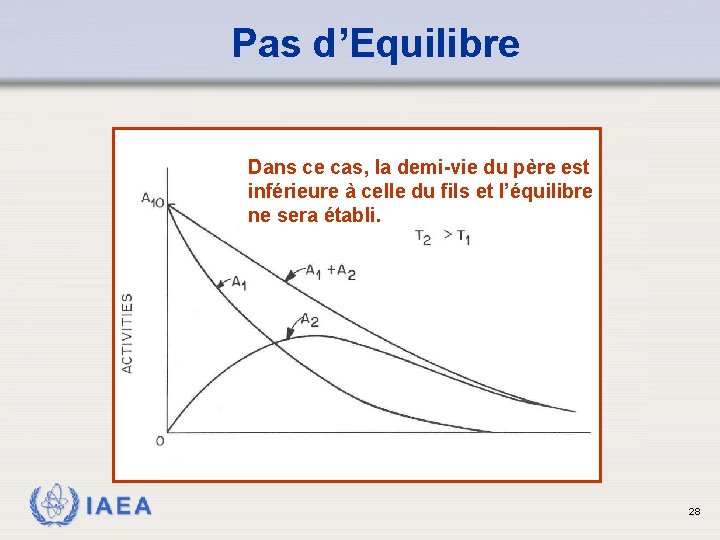
Pas d’Equilibre Dans ce cas, la demi-vie du père est inférieure à celle du fils et l’équilibre ne sera établi. IAEA 28

Résumé Ø L’activité a été définie et les unités ont été discutés Ø la constante de décroissance a été définie Ø La demi-vie a été définie en fonction de la constante de décroissance Ø l’équation de la décroissance radioactive a été dérivée Ø dérivée de la vie moyenne en fonction de la demi-vie Ø L’équilibre a été défini Ø La cas où il n’y a pas d’équilibre a été aussi défini IAEA 29

Où trouver plus d’informations Ø Cember, H. , Johnson, T. E, Introduction to Health Physics, 4 th Edition, Mc. Graw-Hill, New York (2009) Ø International Atomic Energy Agency, Postgraduate Educational Course in Radiation Protection and the Safety of Radiation Sources (PGEC), Training Course Series 18, IAEA, Vienna (2002) IAEA 30
- Slides: 30