Radical Functions Copyright Cengage Learning All rights reserved

Radical Functions Copyright © Cengage Learning. All rights reserved. 8

8. 1 Radical Functions Copyright © Cengage Learning. All rights reserved.

Objectives § Use radicals that model applications. § Find the domain and range of a radical function in a context. § Recognize the graphs of radicals with odd and even indexes. § Find the domain and range of a radical function. § Graph radical functions. 3

Radical Functions The name radical is given to the symbol , and the expression inside of the radical is called the radicand. The word radical is also used to describe any function that uses a radical with variables in the radicand. When we want to represent a root other than a square root, we indicate that by using an index in the nook of the radical symbol. Whenever the index is higher than 2, the radical is considered a higher root. 4

Radical Functions 5

Radical Functions That Model Data 6

Example 1 – A radical model from zoology Allometry is the study of how some aspect of the physiology of a certain species of animal changes in proportion with a change in body size. For example, a study of neotropical butterflies at the Department of Zoology, University of Texas– Austin, studied the relationship of the airspeeds during natural free flight and several characteristics of the butterflies. 7

Example 1 – A radical model from zoology cont’d One relationship that was studied was between the body mass (in grams) of the butterfly and its mean forward airspeed, velocity (in meters per second). A sample of the data collected is given in the table. Source: The Journal of Experimental Biology, 191, 125– 139 (1994) as found at jeb. biologist. org. 8

Example 1 – A radical model from zoology cont’d a. Create a scatterplot of the data in the table. b. An estimated model for these data is given by the following. Let V(m) be the mean forward airspeed in meters per second for neotropical butterflies and let m be the body mass of the butterfly in grams. V(m) = 8. 7 9

Example 1 – A radical model from zoology cont’d i. Graph this model with the given data. ii. How well does it fit the data? iii. Describe the general shape of the graph. c. Estimate the airspeed of a butterfly with a body mass of 0. 5 gram. d. Give a reasonable domain and range for this model. e. Use the graph to estimate the body mass of a butterfly that has an airspeed of 5 meters per second. 10

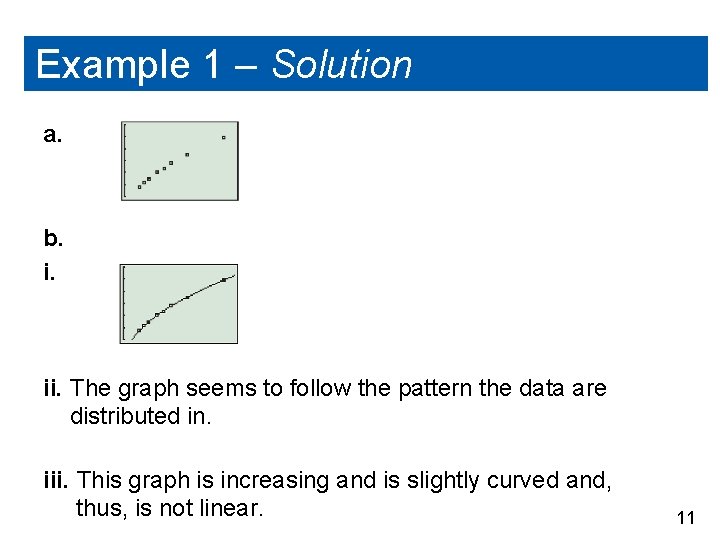
Example 1 – Solution a. b. i. ii. The graph seems to follow the pattern the data are distributed in. iii. This graph is increasing and is slightly curved and, thus, is not linear. 11

Example 1 – Solution cont’d c. We are given the body mass of the butterfly, so we can let m = 0. 5, and we get. V(0. 5) = V(0. 5) 6. 15 Therefore, a butterfly with a body mass of 0. 5 gram would have a mean forward airspeed of approximately 6. 15 meters per second. 12

Example 1 – Solution cont’d d. Because the input variable represents the body mass of a butterfly, we should choose only small positive numbers. Therefore, one possible domain could be [0. 08, 0. 75]. Because the range will be the lowest point to highest point within the domain, we would get a range of [2. 46, 7. 53]. 13

Example 1 – Solution cont’d e. Using the graph and trace, we get the following. Therefore, a butterfly with a body mass of about 0. 34 gram will have an airspeed of about 5 meters per second. 14

Domain and Range of Radical Functions 15

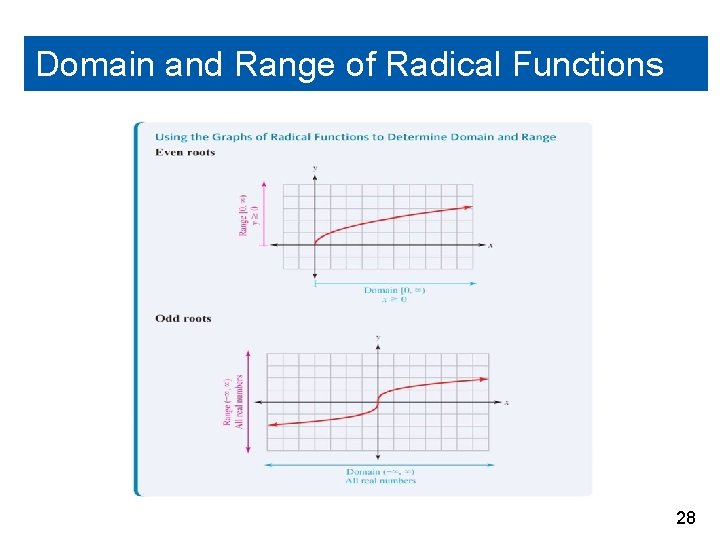
Domain and Range of Radical Functions Let’s look at the graphs of several radical functions and consider the domain and range of those functions in problems that are not restricted by an application. Whether the root is odd or even makes a difference in the shape of the graph as well as what its domain and range are. You should note that in the real number system, even roots cannot have negative numbers under the radical and have only values that make the radicand nonnegative as part of their domain. 16

Domain and Range of Radical Functions Odd roots do not have this restriction because negatives are possible under an odd root and typically have all real numbers as a domain. We can find the domain of a radical function by first determining whether the radical is an even or odd root. If the root is even we set the radicand greater than or equal to zero and solve. If the root is odd, then we know the domain is all real numbers. It is easiest to determine the range of a radical function by using the graph. 17

Domain and Range of Radical Functions 18

Example 4 – Domain and range of radical functions Give the domain and range of the following radical functions. a. f (x) = b. g(x) = c. f (x) = d. h(x) = 19

Example 4(a) – Solution cont’d The function f (x) = is an even root, so the domain can include only values that make the radicand nonnegative. Solve the following inequality. x+3 0 x – 3 Therefore, the domain of this function is x – 3. 20

Example 4(a) – Solution cont’d The lowest point on the graph is zero. The graph continues upward to infinity, so we get a range of [0, ). We can confirm this domain and range by looking at its graph on the calculator. 21

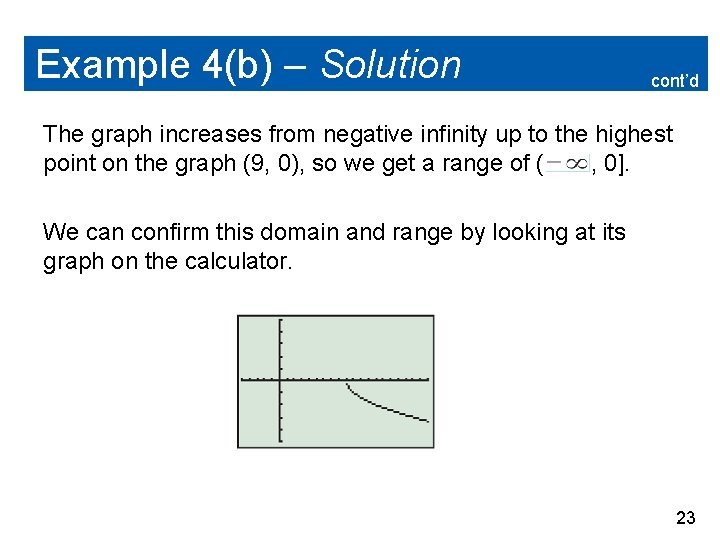
Example 4(b) – Solution cont’d The function g(x) = – is an even root, so the domain can include only values that make the radicand nonnegative. Solve the following inequality. x– 9 0 x 9 Therefore, the domain of this function is x 9. 22

Example 4(b) – Solution cont’d The graph increases from negative infinity up to the highest point on the graph (9, 0), so we get a range of ( , 0]. We can confirm this domain and range by looking at its graph on the calculator. 23

Example 4(c) – Solution cont’d The function f (x) = is a cube root, which means that it is an odd root. The radicand may be either positive or negative, so the domain would include all real numbers. The range will also be all real numbers because the graph goes down to negative infinity and up to positive infinity. Looking at the graph of this function confirms this. 24

Example 4(d) – Solution cont’d Because the function h(x) = is an even root, the radicand must be nonnegative. Although the radicand looks negative, if x is a negative number, then –x will be a positive number. We solve the following inequality, –x + 5 0 –x – 5 To isolate x, we divide both sides by – 1. Remember that we need to reverse the inequality symbol whenever we multiply or divide both sides by a negative number. x 5 25

Example 4(d) – Solution cont’d Therefore, the domain of this function is x 5. The lowest point on the graph of this function is (5, 0), so the range will start at zero. The function continues up to infinity, so we get a range of [0, ). We can confirm this domain and range by looking at its graph on the calculator. 26

Domain and Range of Radical Functions If you are given the graph of a radical function, you can determine the domain by looking for which values of the input (x) are represented by the graph. The range continues to be the lowest output value to the highest output value within the domain. 27

Domain and Range of Radical Functions 28

Example 5 – Domain and range of radical functions Give the domain and range of the following radical functions. a. b. 29

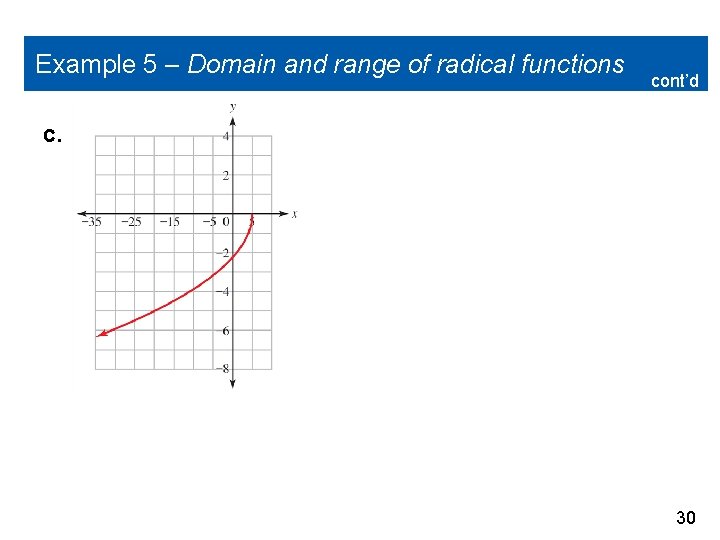
Example 5 – Domain and range of radical functions cont’d c. 30

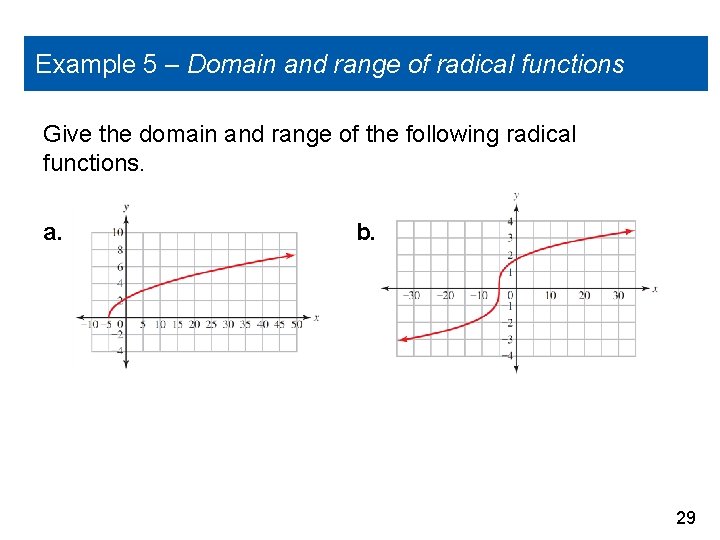
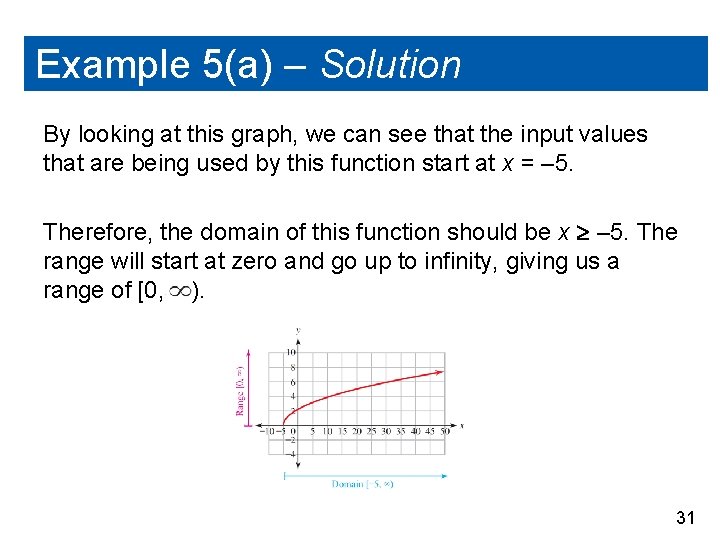
Example 5(a) – Solution By looking at this graph, we can see that the input values that are being used by this function start at x = – 5. Therefore, the domain of this function should be x – 5. The range will start at zero and go up to infinity, giving us a range of [0, ). 31

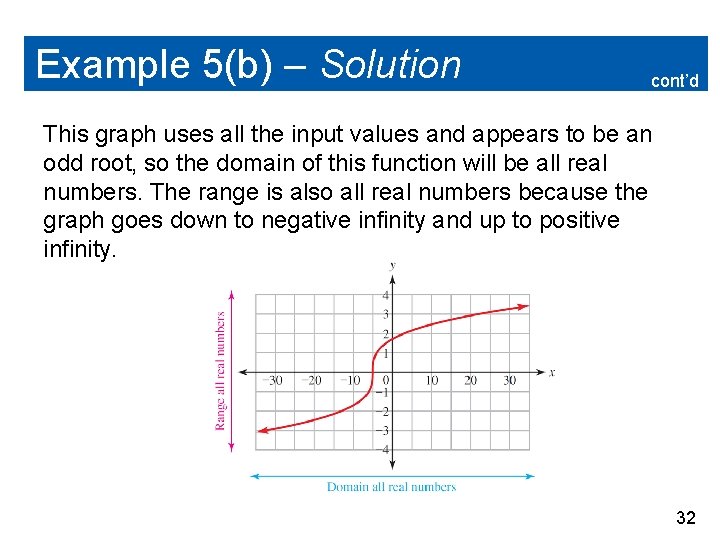
Example 5(b) – Solution cont’d This graph uses all the input values and appears to be an odd root, so the domain of this function will be all real numbers. The range is also all real numbers because the graph goes down to negative infinity and up to positive infinity. 32

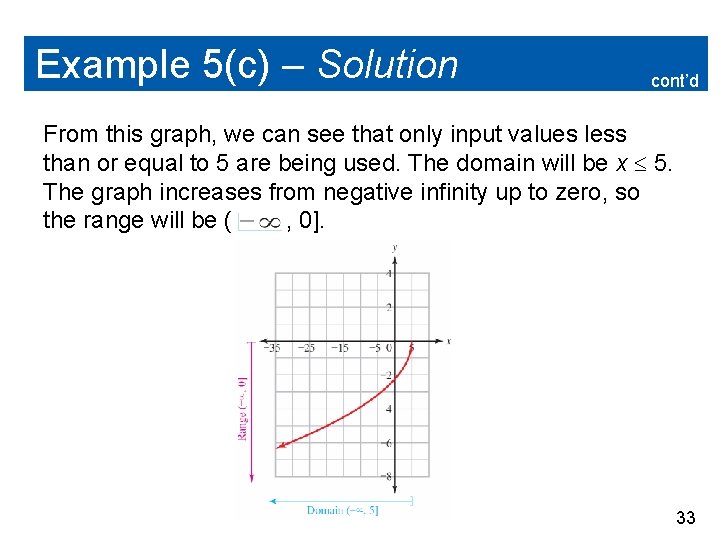
Example 5(c) – Solution cont’d From this graph, we can see that only input values less than or equal to 5 are being used. The domain will be x 5. The graph increases from negative infinity up to zero, so the range will be ( , 0]. 33

Graphing Radical Functions 34

Graphing Radical Functions Radicals with even indexes have restricted domains, and their graphs only go in one direction. Radicals with odd indexes have unrestricted domains and their graphs go in both directions. When graphing a radical function, start by finding the domain and then choose values of x within the domain and build a table of points to plot. If we are careful with the points that we choose, the values will be easier to graph. 35

Graphing Radical Functions Knowing the perfect squares and perfect cubes can really help us to choose nicer input values. 36

Example 6 – Graphing radical functions Sketch the graph of the following radical functions. a. f (x) = b. f (x) = c. g(x) = d. h(x) = 37

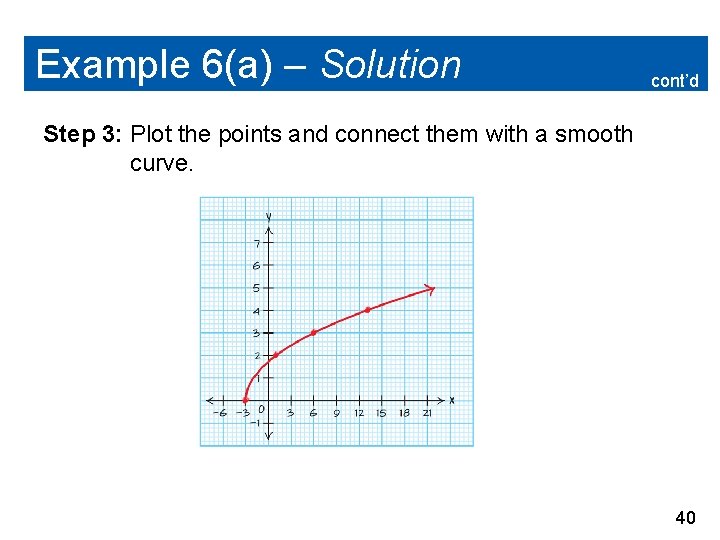
Example 6(a) – Solution Step 1: Find the domain of the radical function. The function f (x) = is an even root, so the radicand must be nonnegative. x+3 0 x – 3 The domain is x – 3. 38

Example 6(a) – Solution cont’d Step 2: Choose x-values within the domain to find points to plot. 39

Example 6(a) – Solution cont’d Step 3: Plot the points and connect them with a smooth curve. 40

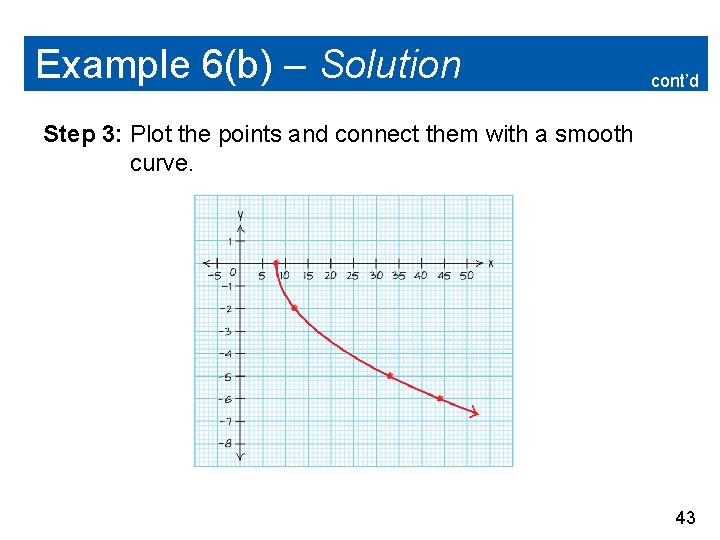
Example 6(b) – Solution cont’d Step 1: Find the domain of the radical function. The function f (x) = is an even root, so the radicand must be nonnegative. x– 8 0 x 8 The domain is x 8. 41

Example 6(b) – Solution cont’d Step 2: Choose x-values within the domain to find points to plot. 42

Example 6(b) – Solution cont’d Step 3: Plot the points and connect them with a smooth curve. 43

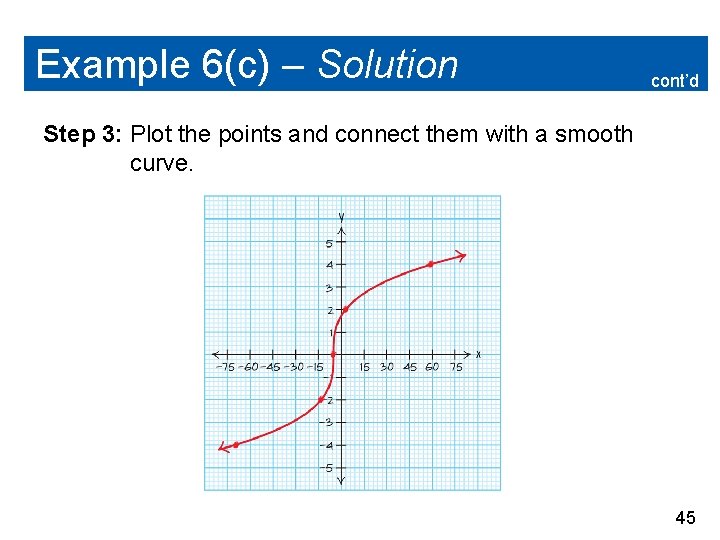
Example 6(c) – Solution cont’d Step 1: Find the domain of the radical function. The function g(x) = is an odd root, so the domain is all real numbers. Step 2: Choose x-values within the domain to find points to plot. 44

Example 6(c) – Solution cont’d Step 3: Plot the points and connect them with a smooth curve. 45

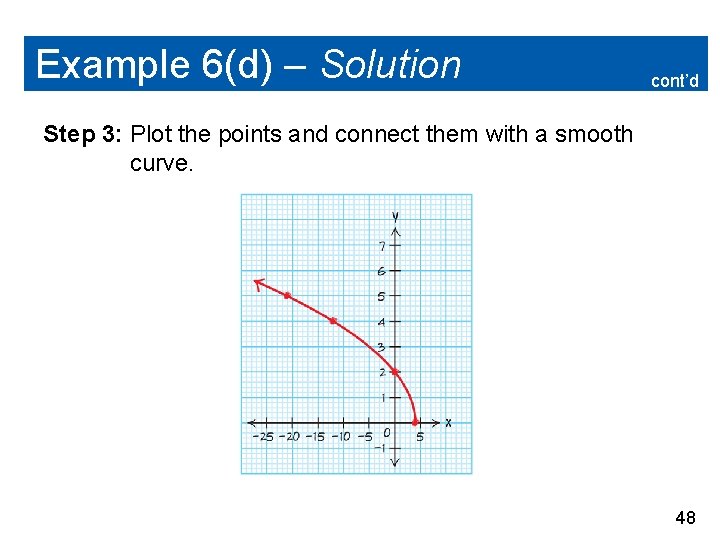
Example 6(d) – Solution cont’d Step 1: Find the domain of the radical function. The function h(x) = is an even root, so the radicand must be nonnegative. 4–x 0 –x – 4 x 4 The domain is x 4. 46

Example 6(d) – Solution cont’d Step 2: Choose x-values within the domain to find points to plot. 47

Example 6(d) – Solution cont’d Step 3: Plot the points and connect them with a smooth curve. 48