Radiative Transfer with Atmospheric Emission Introduction to radiative





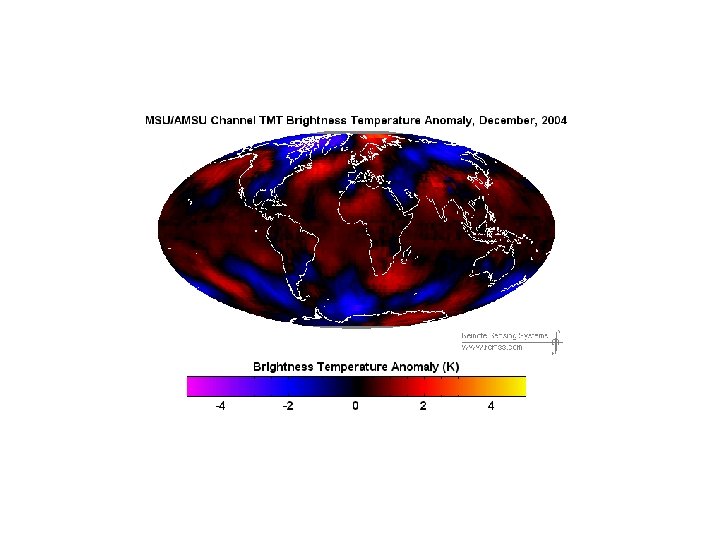
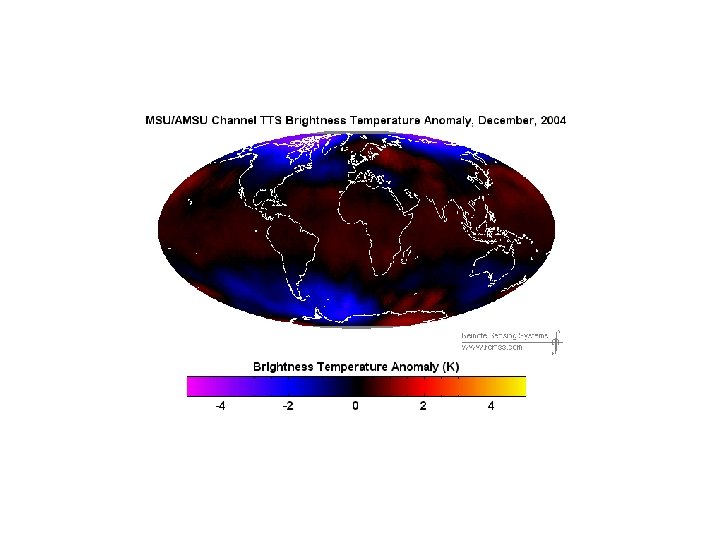
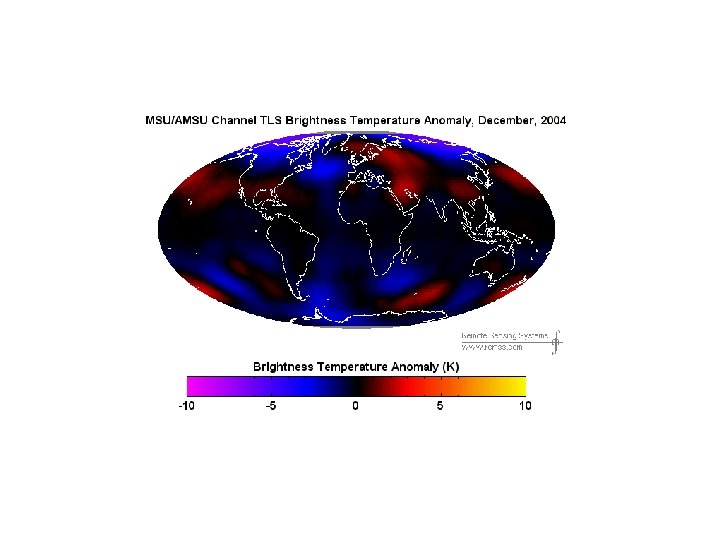


- Slides: 26

Radiative Transfer with Atmospheric Emission Introduction to radiative transfer in an absorptive atmosphere



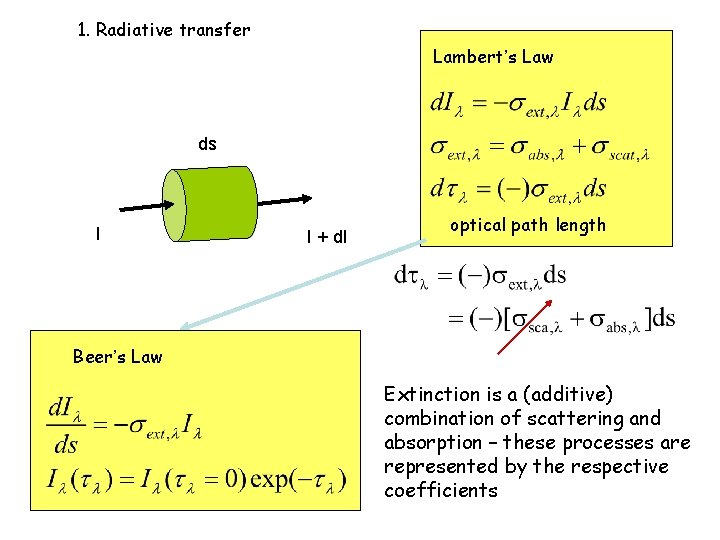
1. Radiative transfer Lambert’s Law ds I I + d. I optical path length Beer’s Law Extinction is a (additive) combination of scattering and absorption – these processes are represented by the respective coefficients

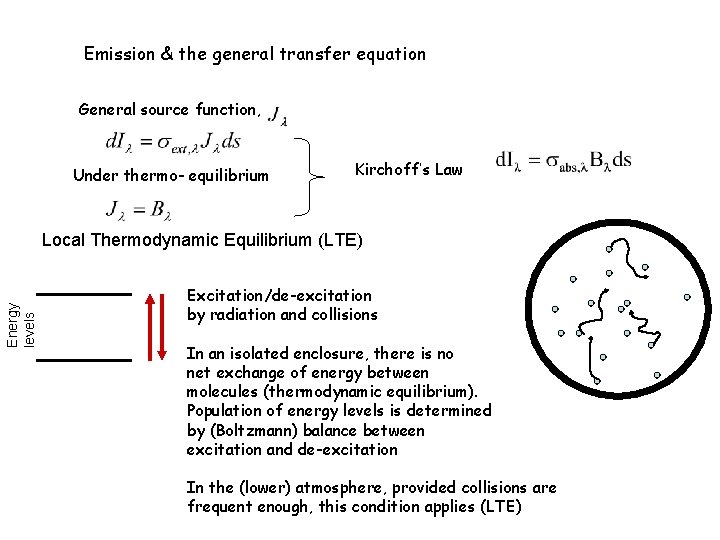
Emission & the general transfer equation General source function, Under thermo- equilibrium Kirchoff’s Law Energy levels Local Thermodynamic Equilibrium (LTE) Excitation/de-excitation by radiation and collisions In an isolated enclosure, there is no net exchange of energy between molecules (thermodynamic equilibrium). Population of energy levels is determined by (Boltzmann) balance between excitation and de-excitation In the (lower) atmosphere, provided collisions are frequent enough, this condition applies (LTE)

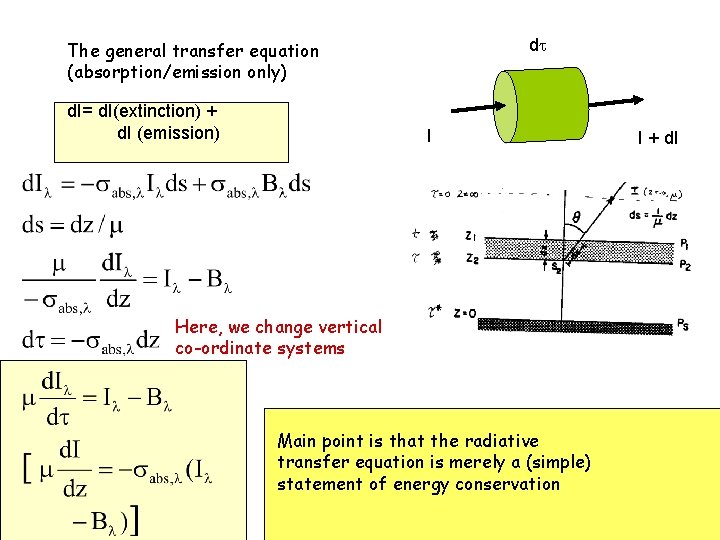
d The general transfer equation (absorption/emission only) d. I= d. I(extinction) + d. I (emission) I I + d. I Insert fig. 4. 3 Here, we change vertical co-ordinate systems Main point is that the radiative transfer equation is merely a (simple) statement of energy conservation

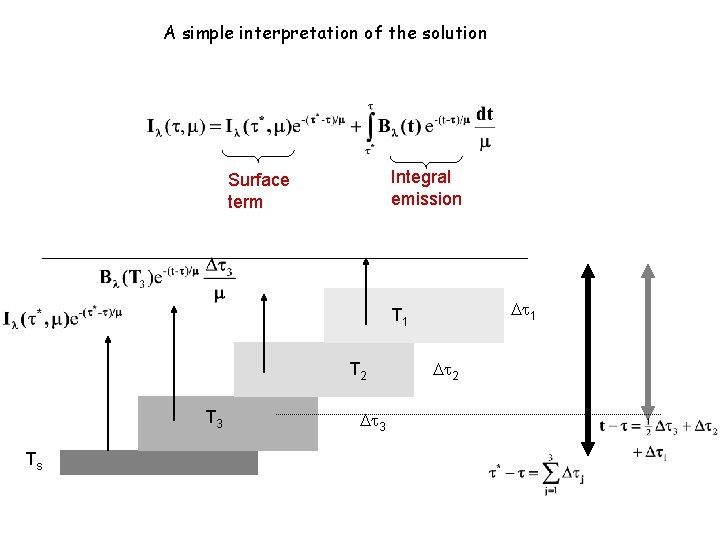
The (general) integral solution You need to be able to derive both the equations of transfer as introduced previously and its general integral solution given here.

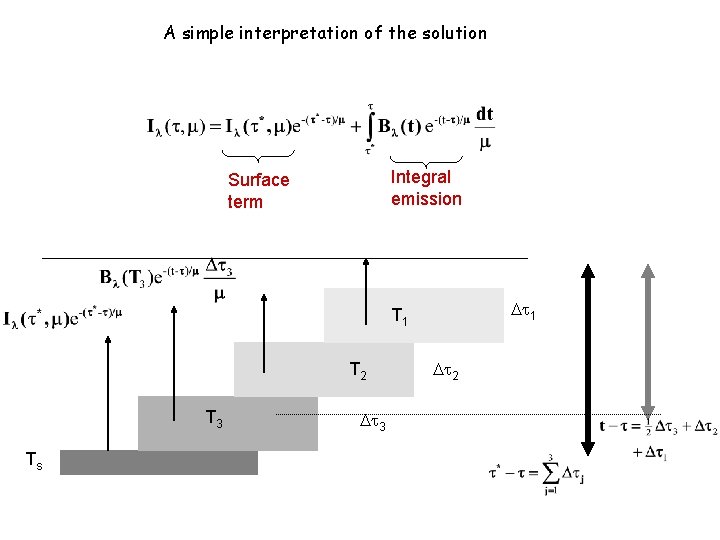
A simple interpretation of the solution Integral emission Surface term 1 T 2 T 3 Ts 3 2

In Microwave, hc/kl. T << 1 Changing notations again (Il becomes Tbl)

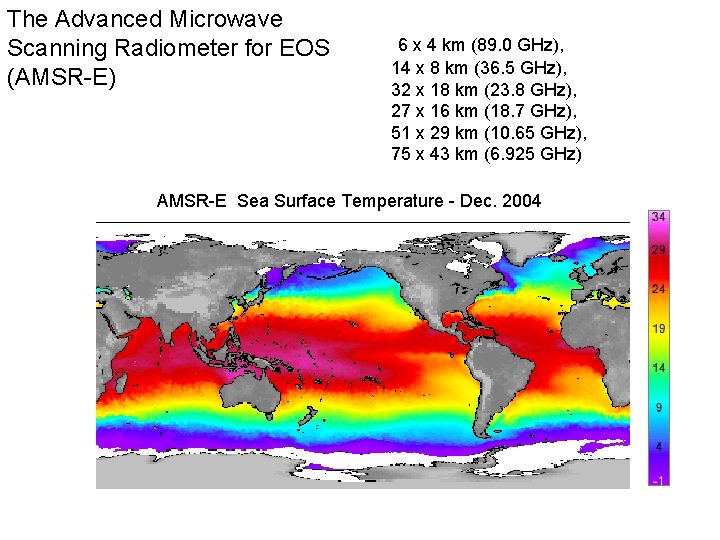
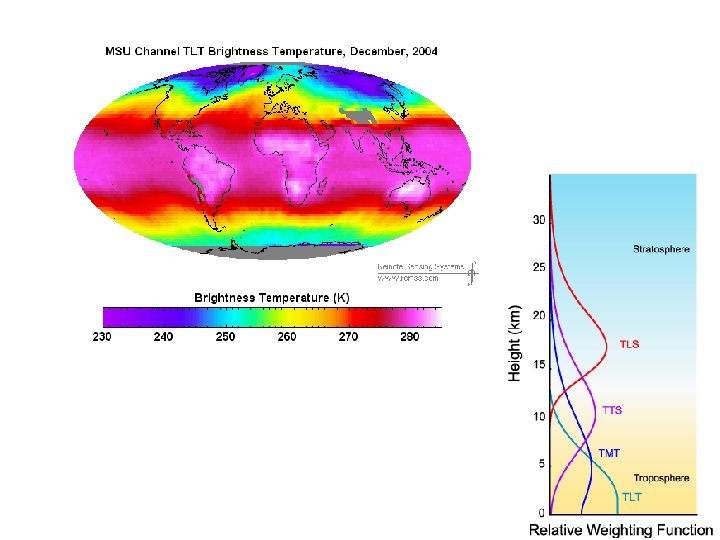
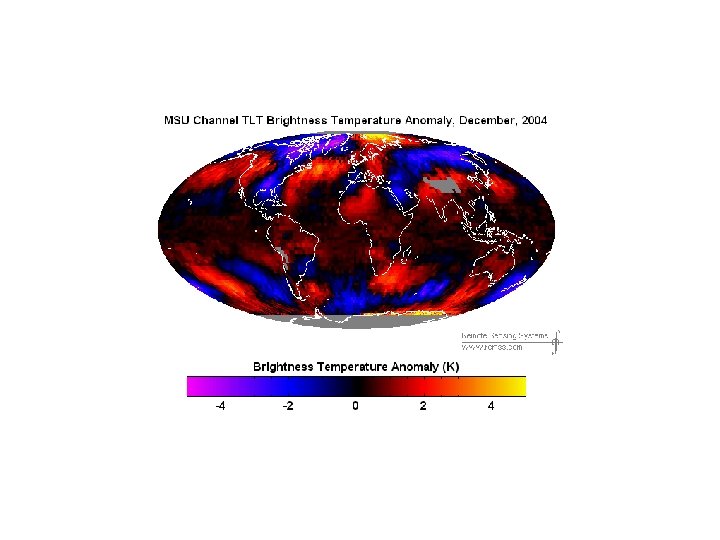
The Advanced Microwave Scanning Radiometer for EOS (AMSR-E) 6 x 4 km (89. 0 GHz), 14 x 8 km (36. 5 GHz), 32 x 18 km (23. 8 GHz), 27 x 16 km (18. 7 GHz), 51 x 29 km (10. 65 GHz), 75 x 43 km (6. 925 GHz) AMSR-E Sea Surface Temperature - Dec. 2004

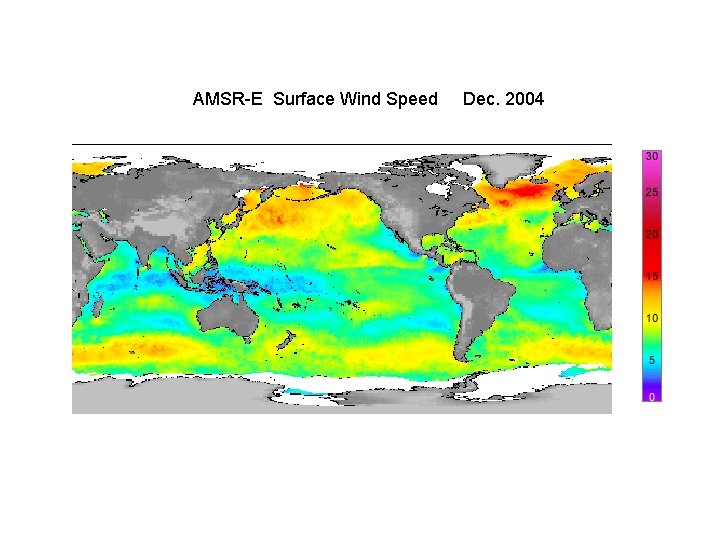
AMSR-E Surface Wind Speed Dec. 2004

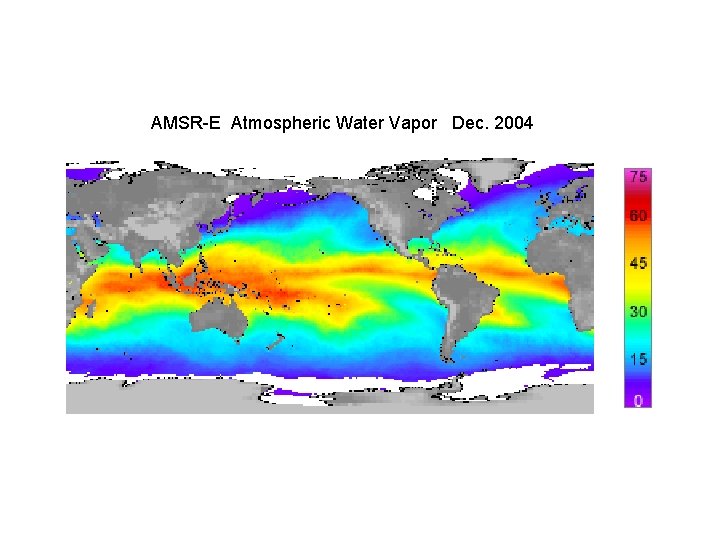
AMSR-E Atmospheric Water Vapor Dec. 2004

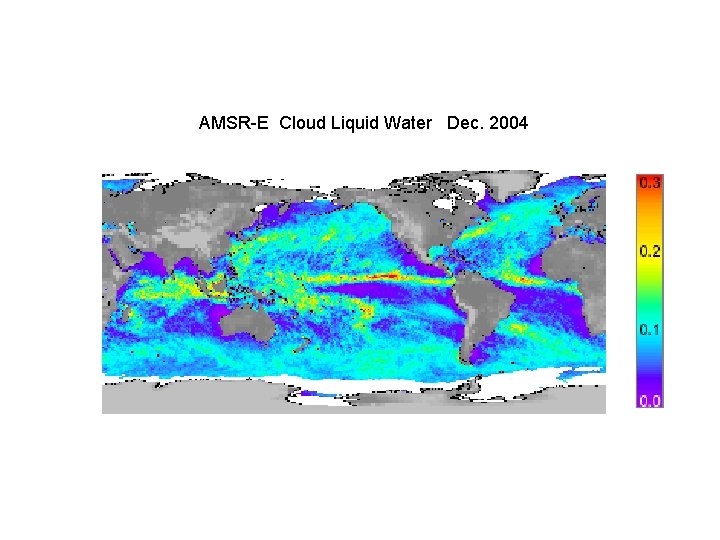
AMSR-E Cloud Liquid Water Dec. 2004

http: //www. ssmi. com/ssmi_description. html Special Sensor Microwave/Imager (SSM/I) data products are produced as part of NASA's Pathfinder Program. Remote Sensing Systems generates SSM/I data products using a unified, physically based algorithm to simultaneously retrieve ocean wind speed (at 10 meters), water vapor, cloud water, and rain rate. This algorithm is a product of 15 years of refinements, improvements, and verifications. While the algorithms have evolved over time, a substantial background to the radiative transfer function used to derive the geophysical parameters is described in the following paper: Wentz, FJ, 1997: A well calibrated ocean algorithm for special sensor microwave / imager, Journal of Geophysical Research, 102, 8703 -8718.

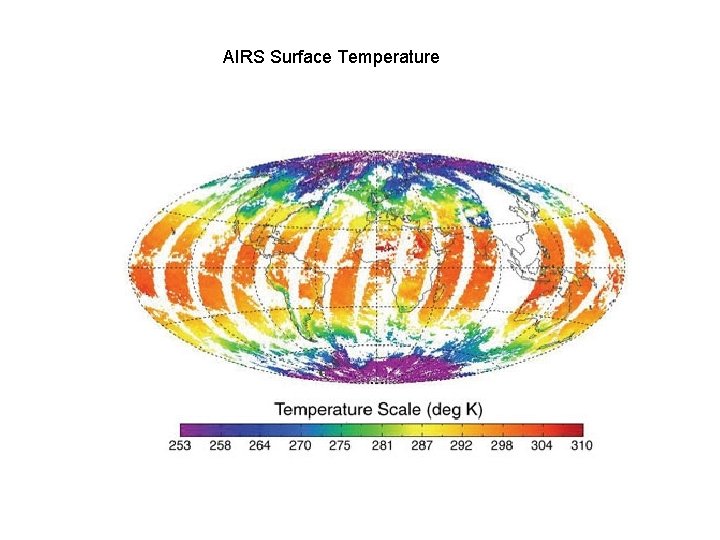
AIRS Surface Temperature

Radiative transfer equation in terms of transmission: In terms of physical height z: The factor weights the Planck function, B(z).

A simple interpretation of the solution Integral emission Surface term 1 T 2 T 3 Ts 3 2

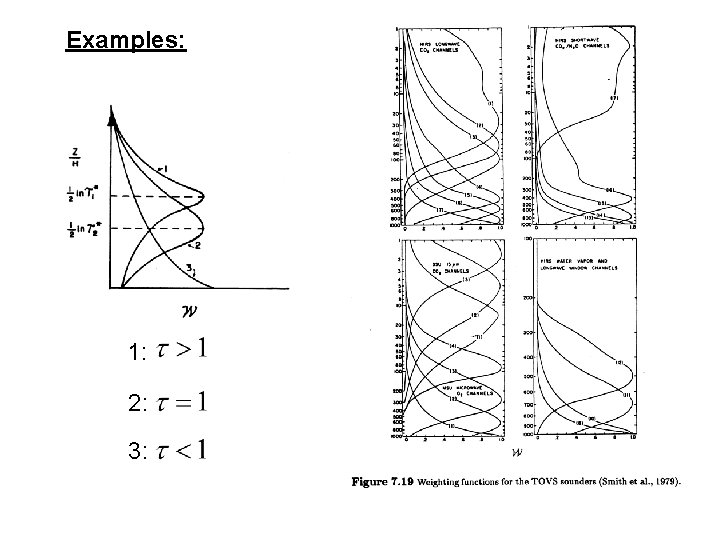
Examples: 1: 2: 3:

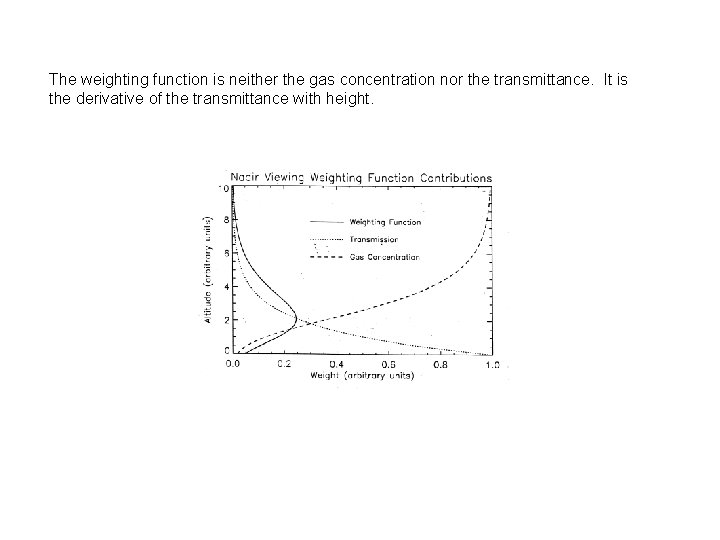
The weighting function is neither the gas concentration nor the transmittance. It is the derivative of the transmittance with height.






Weighting Functions for Limb Sounding Radiative transfer equation: where is the path through the atmosphere.

Advantages of Limb Sounding by Emission • None of the emitted radiation seen by the satellite originates below the tangent height: allows for relatively high vertical resolution. • The surface has no influence on the measured intensities. • Due to the geometry of limb sounding, considerably more emitting gas is encountered along grazing paths than on straight ones increasing the instrument sensitivity to gases of low concentration. • Also, due to paths being high in the atmosphere, effects of pressure broadening are reduced. Disadvantages of Limb Sounding by Emission • Very sensitive to aerosol in the lower stratosphere. • Often cannot be used in the troposphere when atmosphere is too optically thick.