Radiation Processes in High Energy Astrophysics Lecture 3

Radiation Processes in High Energy Astrophysics Lecture 3: basic processes and concepts Felix Aharonian Dublin Institute for Advanced Studies, Dublin Max-Planck Institut fuer Kernphysik, Heidelberg

interactions with matter E-M: bremsstrahlung: e N(e) => e’ N (e) pair production N(e) => e+e- N (e) e+e- annihilation e+e- => (511 ke. V line) pp ( ) => , K, … , K, => e => also in the low energy region Nuclear: p A => A* => A’ n Strong: n p => D (2. 2 Me. V line)

interactions with radiation and B-fields Radiation field E-M processes: inverse Compton: pair production e (B) => e’ (B) => e+e- p > , K, … , K, => e => ’ B-field synchrotron e (p) B => S processes: pair production B => e+e-

leptonic or hadronic? gamma-rays produced by electrons and protons/nuclei often are (wrongly) called leptonic and hadronic interactions but it is more appropriate to call them as E-M (electromagnetic) and S (strong) examples: (i) synchrotron radiation of protons - pure electromagnetic process interaction of hadrons without production of neutrinos (ii) photon-photon annihilation => + - => neutrinos, antineutrinos production of neutrinos by photons as parent particles E-M S are calculated with high accuracy and confirmed experimentally are well studied experimentally and explained theoretically

calculations of gamma-ray energy spectra and fluxes one needs two functions: differential cross-section energy distribution of parent particles

Differential cross section: Integral cross section: Particle Distribution:

Cross-sections, mean free paths, cooling times cross-section <==> probability of interaction (E), (E, E’) [cm 2] f - coefficient of inelasticity: mean free path: cooling time: = d n f=(Ei-Ef)/Ei =1/( n) [cm] tcool=1/(f n c) [s] effective mechanism of production? When tcool is smaller than (1) the timescales characterizing other radiative and non-radiative (e. g. adiabatic, escape time, etc. ) losses, and (2) the intrinsic dynamical timescales characterizing the source (acceleration time, age of the source, etc. )

distributions of charged parent particles three different approaches: (i) assume a production mechanism and then adopt a particle (electron or proton) energy spectrum, d. N/d. E, to fit the data should be treated no more than a fit (ii) assume an injection spectrum of particles, Q(E), calculate the particle spectrum, d. N/d. E, at given time for given radiative (e. g. synchrotron IC, photomeson, etc. ), and non-radiative (e. g. adiabatic, escape) losses, and see weather can you explain the gamma-ray (radio , X-ray) data works if the particle acceleration and -ray production regions are separated (iii) assume an acceleration process (e. g. diffusive shock acceleration, turbulent acceleration, etc. ), derive and solve the relevant equation(s), obtain the particle spectrum, d. N/d. E, and see weather can you explain the gamma-ray (radio, X-ray, …) data in many cases the only correct approach to follow

general kinetic equation that describes the evolution of particle distribution f(E, r, t) including the diffusion, convection, energy losses and the acceleration terms (e. g. Ginzburg & Sirovatskii 1964), in many cases the acceleration and radiation production regions are separated, then where steady-state solution

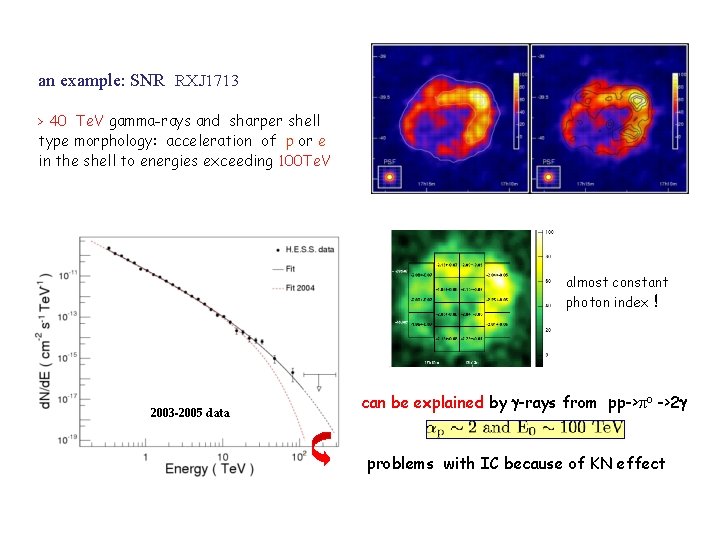
an example: SNR RXJ 1713 > 40 Te. V gamma-rays and sharper shell type morphology: acceleration of p or e in the shell to energies exceeding 100 Te. V almost constant photon index ! 2003 -2005 data can be explained by g-rays from pp-> o ->2 g problems with IC because of KN effect

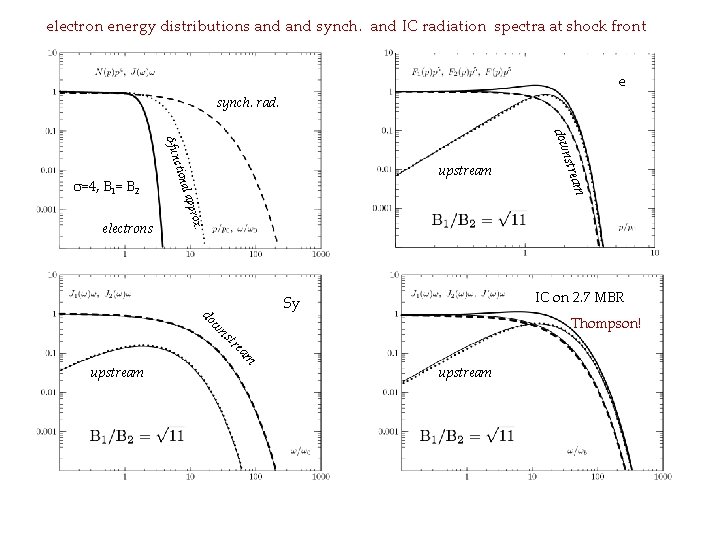
an example: diffusive shock acceleration of electrons in the Bohm diffusion regime; losses dominated by synchrotron radiation (*) E 0 almost coincides with the value derived from tacc = t synch the spectrum of synchrotron radiation at the shock front Synchrotron cutoff energy approximately 10 times h V. Zirakashvili, FA 2007 (*) it is very different from the “standard” assumption E exp[-E/E 0]

electron energy distributions and synch. and IC radiation spectra at shock front e synch. rad. . IC on 2. 7 MBR Sy Thompson! w do am e tr ns upstream prox al ap ction electrons nstr dow -fun =4, B 1= B 2 upstream

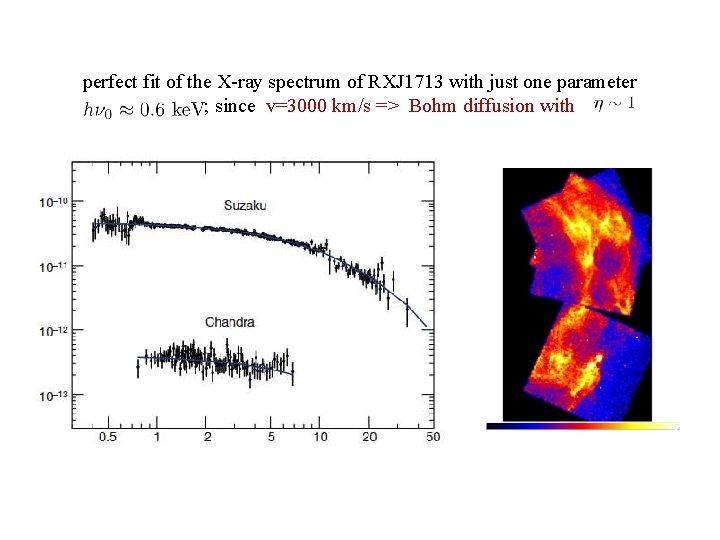
perfect fit of the X-ray spectrum of RXJ 1713 with just one parameter ; since v=3000 km/s => Bohm diffusion with

energy distibutions of particles acceleration (injection) spectrum of particles; generally power-law with high-energy cutoff determined by the condition “acceleration rate=energy loss rate” or taa=tcool later (in the gamma-ray production region) the particle energy psectrum is changed due to energy losses: the steady state solutions for power-law injection (e. g. bremsstrahlung, pp, adiabatic) - no spectral change (e. g. synchrotron, IC (Tompson)) - steeper (e. g. ionozation) -harder (e. g. IC Klein-Nishina) - much harder

quick estimates of -ray fluxes and spectra this can be done, in many cases with a surprisingly good accuracy, using cooling times (for energy fluxes) F = Wp(e)/4 d 2 tcool and -functional approximation (for energy spectra) using the relation <E >=f(Ep(e)) but be careful with -functional approximations … this may lead to wrong results

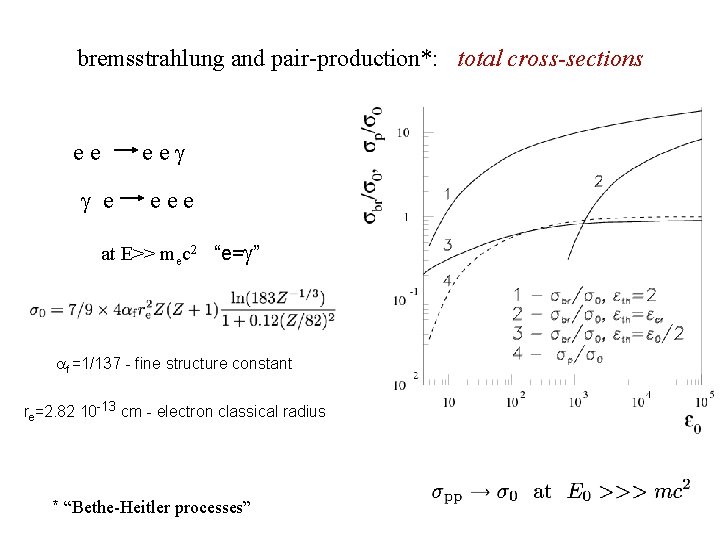
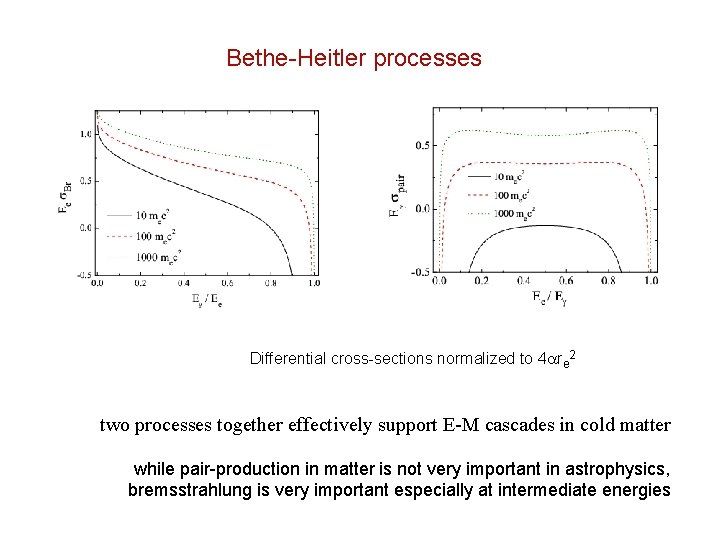
bremsstrahlung and pair-production*: total cross-sections ee e eee at E>> mec 2 “e= ” f =1/137 - fine structure constant re=2. 82 10 -13 cm - electron classical radius * “Bethe-Heitler processes”

Differential cross-sections of B-H processes Bremsstrahlung Pair-production

Bethe-Heitler processes Differential cross-sections normalized to 4 re 2 two processes together effectively support E-M cascades in cold matter while pair-production in matter is not very important in astrophysics, bremsstrahlung is very important especially at intermediate energies

some basic features of bremsstrahlung cooling time: spectrum of -rays from a single electron: 1/E power-law distribution of electrons: -ray spectrum: an example: interstellar medium: repeats the shape of electrons! electron injection spectrum (1) at low energies -1 because losses are dominated by ionization (2) at intermediate energies because losses are dominated Bremsstrahung (3) at very high energies +1 because losses are dominated Synch. /IC (4) at very low (ke. V) energies - only <10 -5 (because of ionization losses)

annihilation of electron-positron pairs astrophysical significance of this process - formation of mec 2=0. 511 Me. V line gamma-ray emission at annihilation of thermalized positrons however if positrons are produced with relativistic energies, a significant fraction - 10 to 20 % of positrons annihilate in flight before they cool down to the temperature of thermal background gas (plasma) power-law spectrum of positrons E+ total cross-section: cooling time: for positrons energies annihilation dominates over bremsstrahlumg

pp -> 0 -> - a major gamma-ray production mechanism s relativistic protons and nuclei produce high energy in inelastic collisions with ambient gas due to the production and decay of secondary particles pions, kaons and hyperons neutral 0 -mesons provide the main channel of gamma-ray production • production threshold • the mean lifetime of 0 -mesons • three types of pions are produced with comparable probabilities • spectral form of pions is generally determined by number o a few (one or two) leading particles (carrying significant fraction of the nucleon energy) • cooling (radiation) time: tpp = 1015 (n/1 cm-3)-1 s

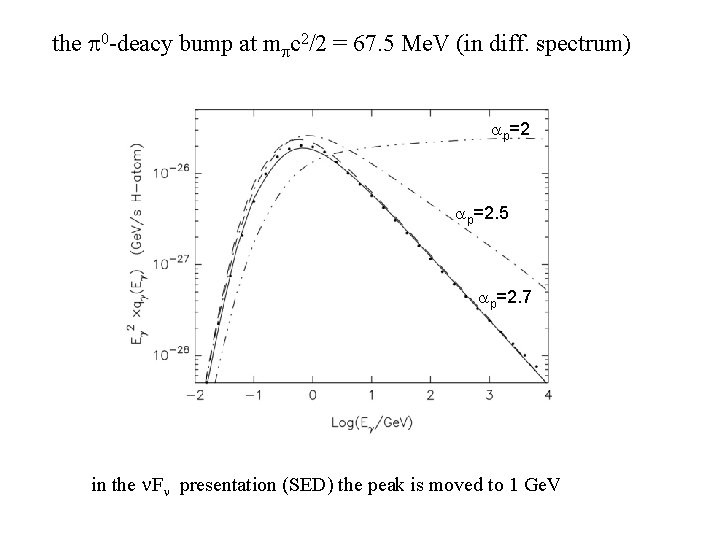
the 0 -deacy bump at m c 2/2 = 67. 5 Me. V (in diff. spectrum) p=2. 5 p=2. 7 in the F presentation (SED) the peak is moved to 1 Ge. V

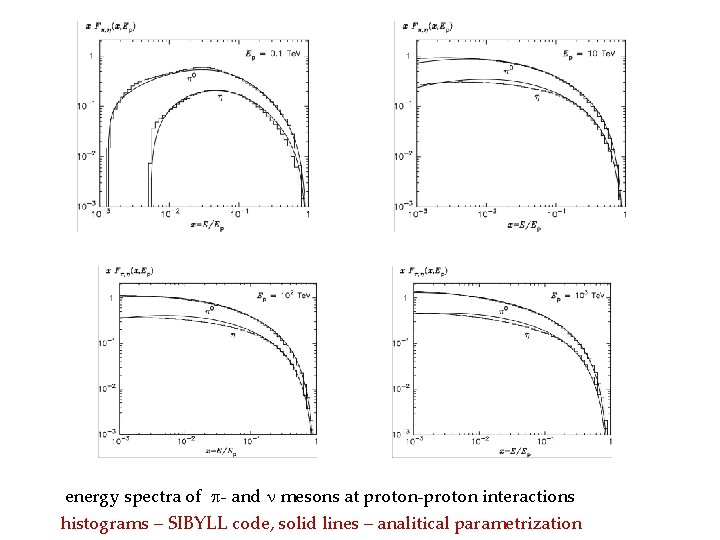
energy spectra of - and mesons at proton-proton interactions histograms – SIBYLL code, solid lines – analitical parametrization

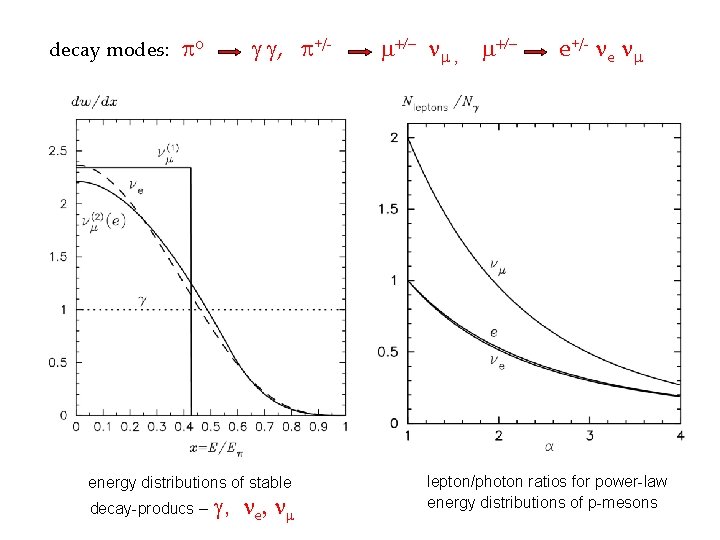
decay modes: o , +/- / e+/- e P energy distributions of stable decay-producs – , e lepton/photon ratios for power-law energy distributions of p-mesons

analytical presentations of energy spectra of , e,

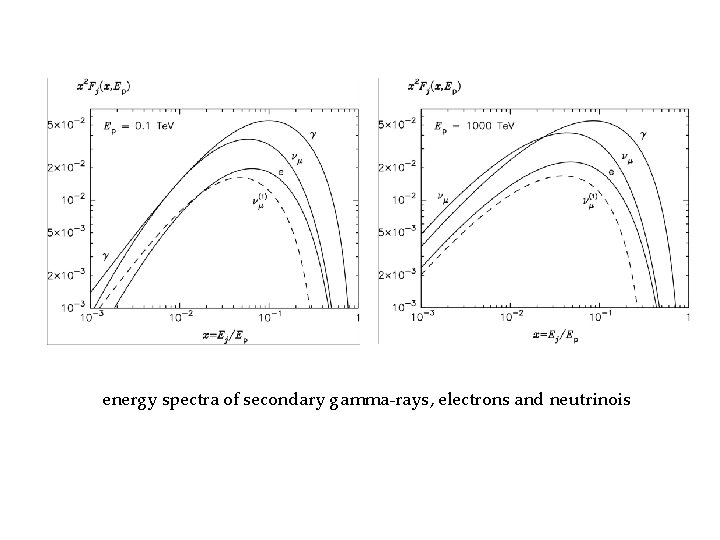
energy spectra of secondary gamma-rays, electrons and neutrinois

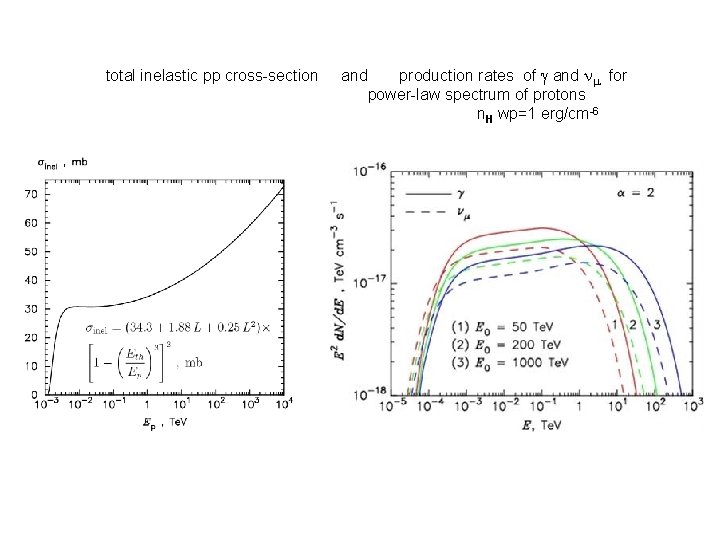
total inelastic pp cross-section and production rates of and for power-law spectrum of protons n. H wp=1 erg/cm-6

interactions with photon fields photon-photon pair production and Compton scattering two processes are tightly coupled - both have large crosssections and work effectively everywhere in the Universe from compact objects like pulsars, Black Holes and Active Galactic Nuclei to large scale structures as clusters of galaxies IC - production process - no energy threshold PP - absorption process: threshold: E E >m 2 c 4(1 -cos )-1 in radiation-dominated environments both processes work together supporting the transport of high energy radiation via electromagnetic Klein-Nishin Cascades

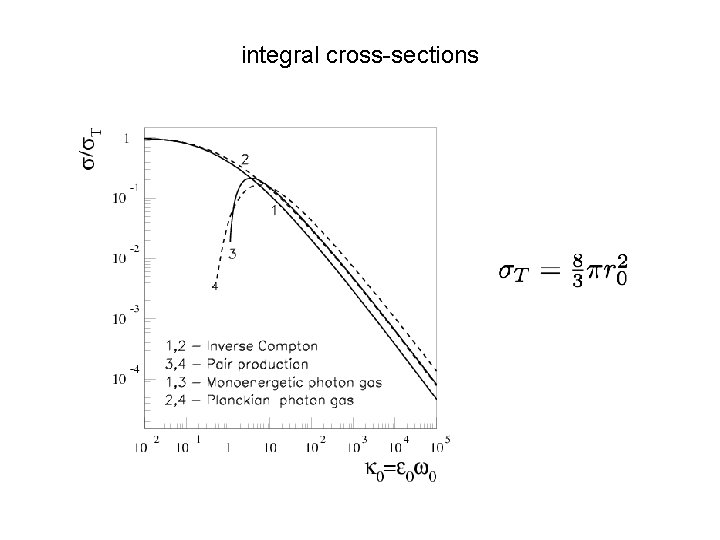
integral cross-sections

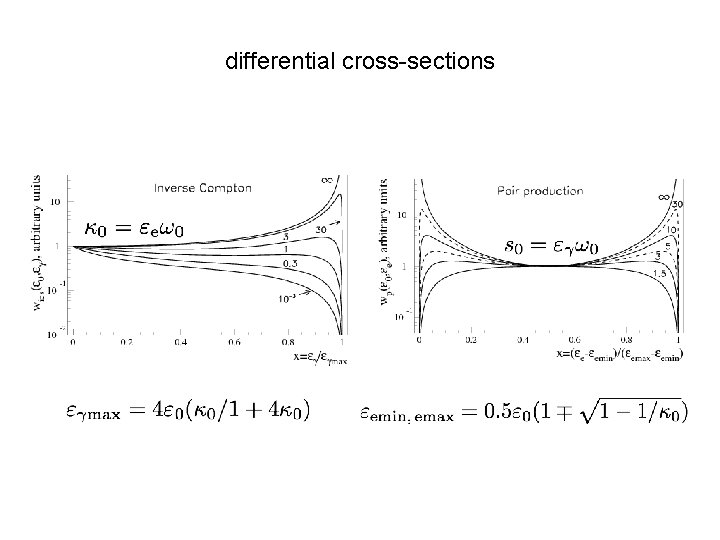
differential cross-sections

energy spectra and cooling times for electron spectrum IC -ray spectrum in nonrealistic (Thompson) limit IC -ray spectrum in realistic (Klein-Nishina) limit energy loss time: cooling time:

some interesting features related to Klein-Nishina effect if IC losses dominate over synchrotron losses K-N effect makes electron spectrum harder ( => -1) but gamma-ray spectrum steeper ( -1+1 -> ) for IC -rays it operates twice in opposite ways => hard -ray spectrum for Synchrotron it works only once => very hard synchrotron spectrum if synchrotron losses dominate over IC losses Synch losses make electron spectrum steeper ( => +1) K-N effect makes gamma-ray spectrum steeper ( 1+1 -> ) => very steep -ray spectrum: +2 => standard synchrotron spectrum: /2

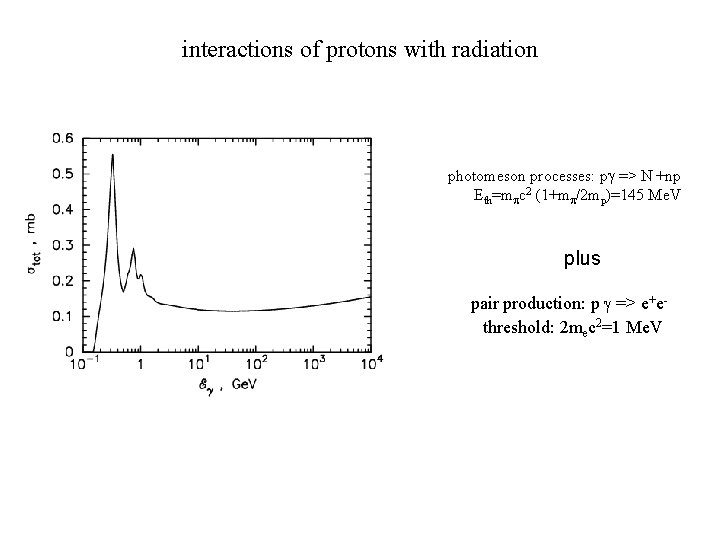
interactions of protons with radiation photomeson processes: p => N +np Eth=m c 2 (1+m /2 mp)=145 Me. V plus pair production: p => e+ethreshold: 2 mec 2=1 Me. V

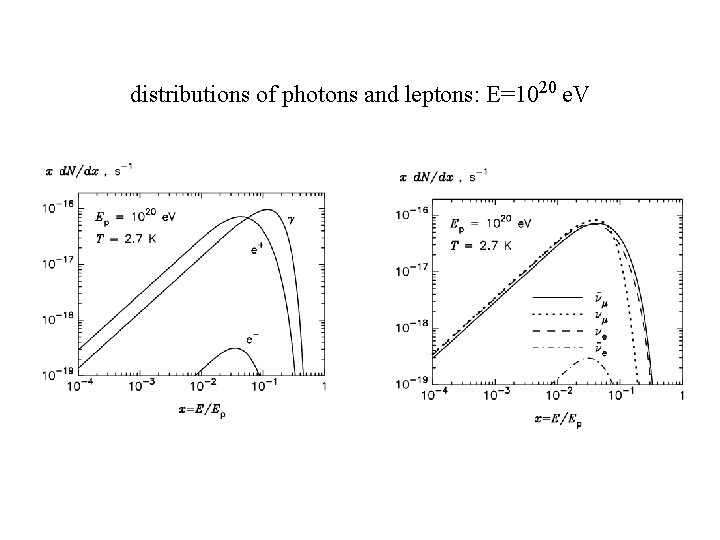
distributions of photons and leptons: E=1020 e. V

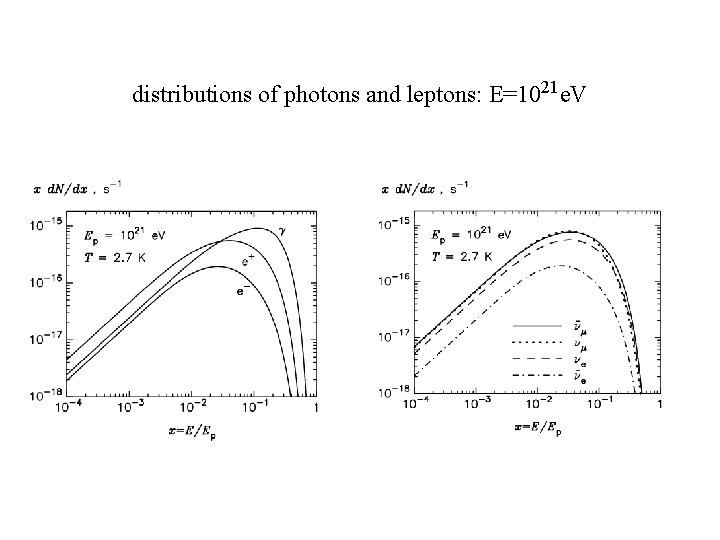
distributions of photons and leptons: E=1021 e. V

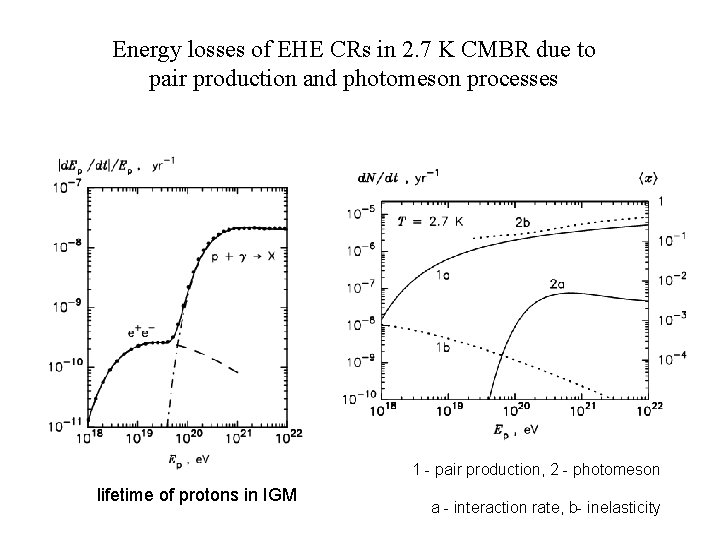
Energy losses of EHE CRs in 2. 7 K CMBR due to pair production and photomeson processes 1 - pair production, 2 - photomeson lifetime of protons in IGM a - interaction rate, b- inelasticity

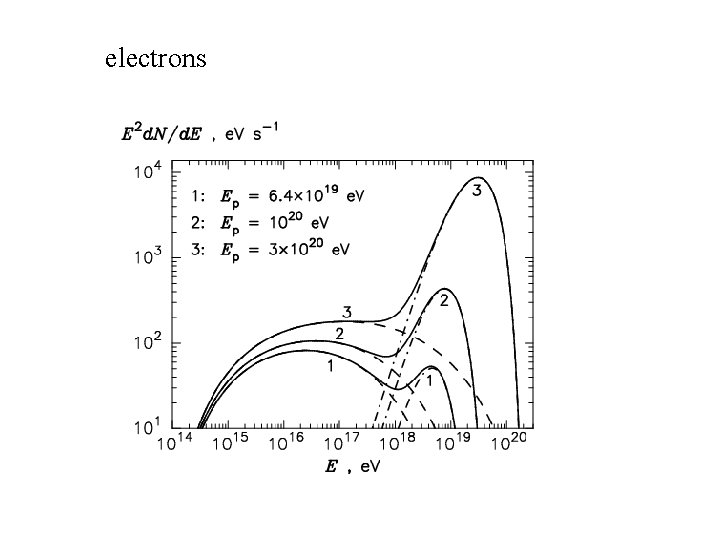
electrons

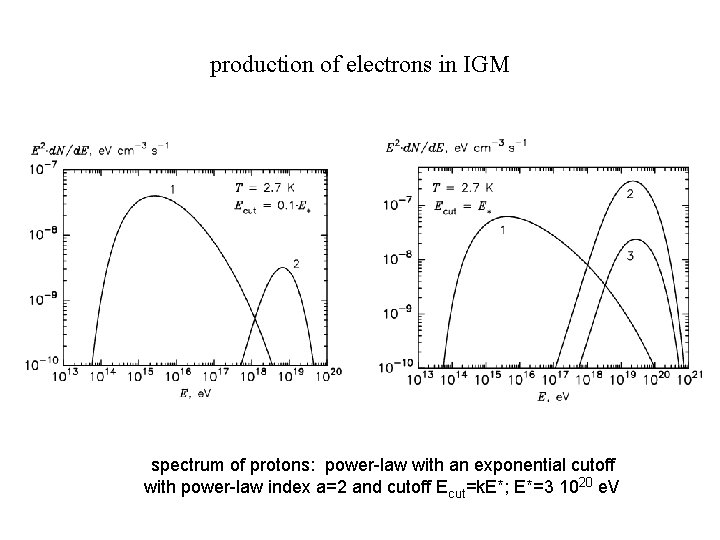
production of electrons in IGM spectrum of protons: power-law with an exponential cutoff with power-law index a=2 and cutoff Ecut=k. E*; E*=3 1020 e. V

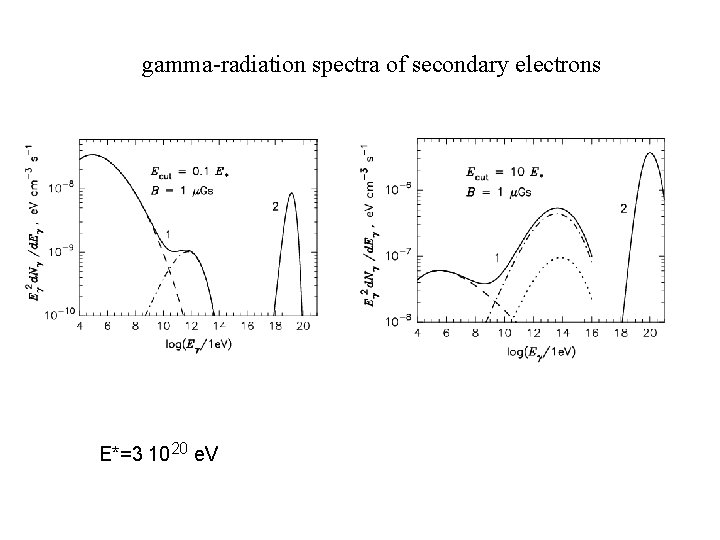
gamma-radiation spectra of secondary electrons E*=3 1020 e. V

interactions with magnetic field photon-photon pair production and Compton scattering many important results of synchrotron theory are obtained within the framework of classical electrodynamics, i. e. or where - critical magnetic field Classical regime: energy of synch. photons << energy of electrons Quantum regime: energy of synch photon is close to electron energy and gamma-rays start effectively interact with Bfield and produce electron-positron pairs probabilities of both processes depend on a single parameter two are tightly coupled and lead to effective pair-cascade development

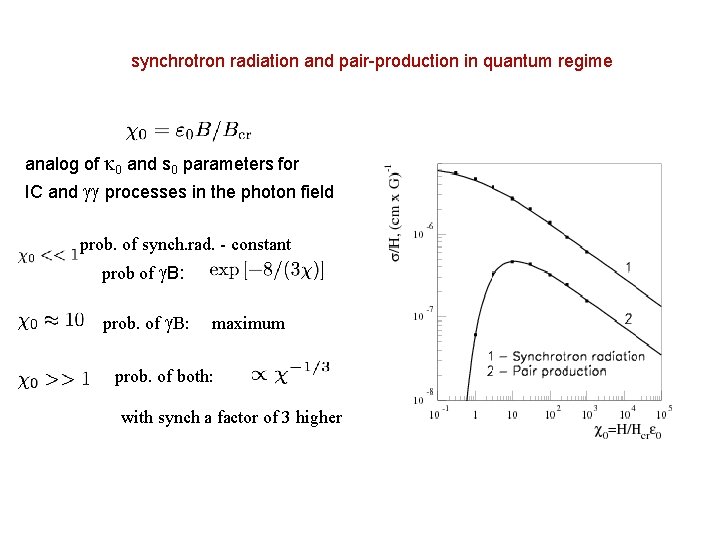
synchrotron radiation and pair-production in quantum regime analog of 0 and s 0 parameters for IC and processes in the photon field prob. of synch. rad. - constant prob of B: prob. of B: maximum prob. of both: with synch a factor of 3 higher

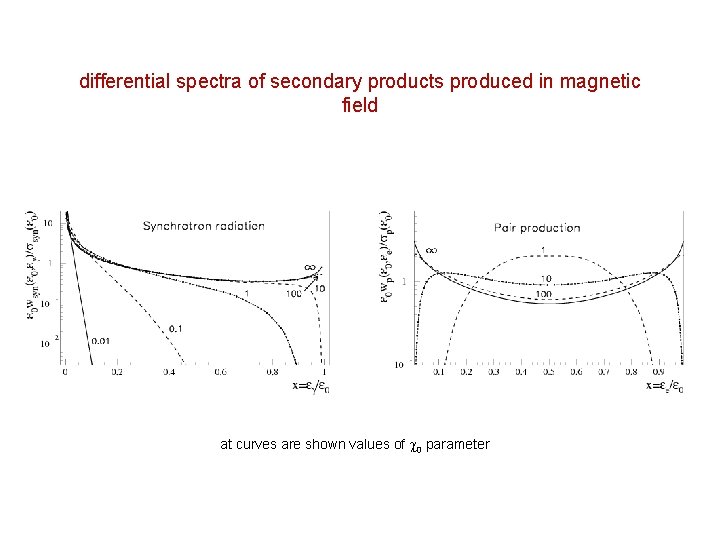
differential spectra of secondary products produced in magnetic field at curves are shown values of parameter