Radiation Processes High Energy Astrophysics jlcmssl ucl ac














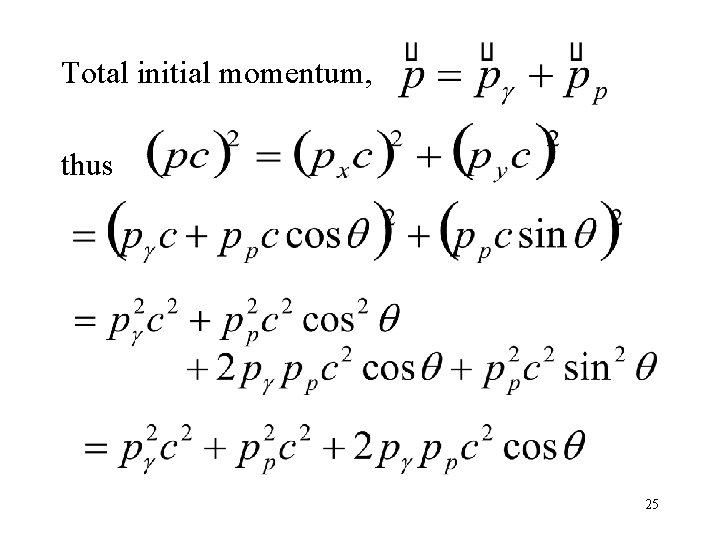
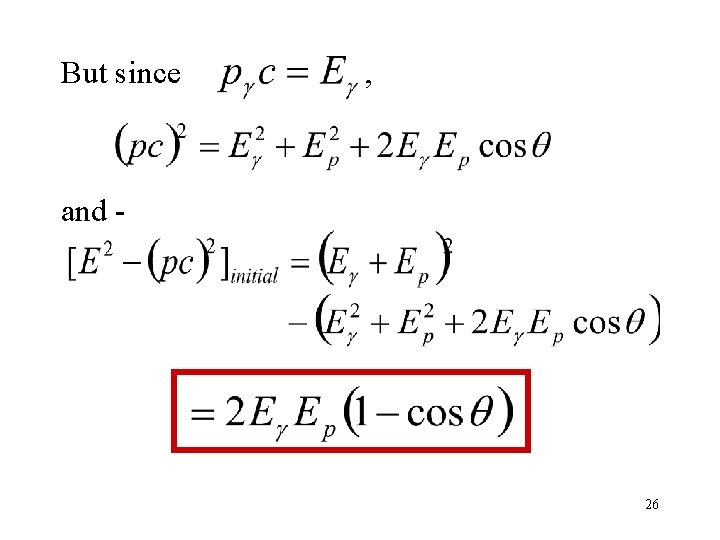














- Slides: 44

Radiation Processes High Energy Astrophysics jlc@mssl. ucl. ac. uk http: //www. mssl. ucl. ac. uk/

1. Interaction of radiation with matter: Photoelectric absorption and the ISM; Thomson and Compton scattering; Pair production; Synchrotron self-absorption; Inverse Compton scattering [2] 2

Absorption Processes Photon emission processes have corresponding absorption processes We will consider X-ray absorption. Emission processes Recombination Absorption process Photoionization Inverse Compton electron scattering e-/e+ annihilation e-/e+ pair production synchrotron emission synchrotron self absorption 3

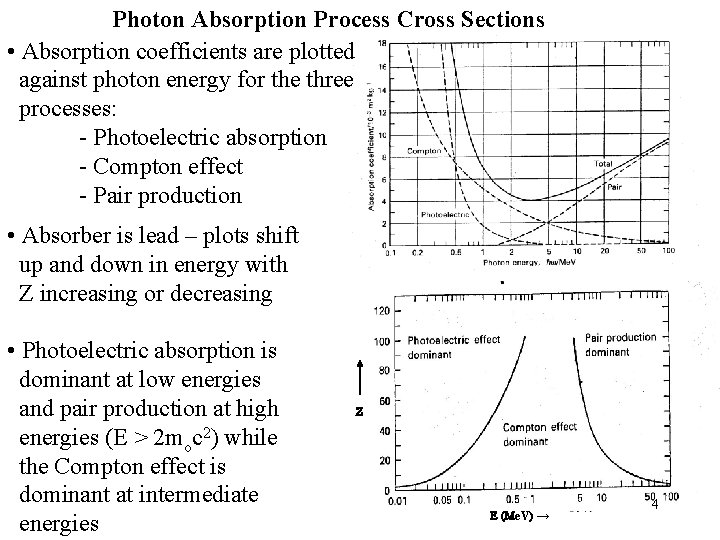
Photon Absorption Process Cross Sections • Absorption coefficients are plotted against photon energy for the three processes: - Photoelectric absorption - Compton effect - Pair production • Absorber is lead – plots shift up and down in energy with Z increasing or decreasing • Photoelectric absorption is dominant at low energies and pair production at high energies (E > 2 moc 2) while the Compton effect is dominant at intermediate energies Z E (Me. V) → 4

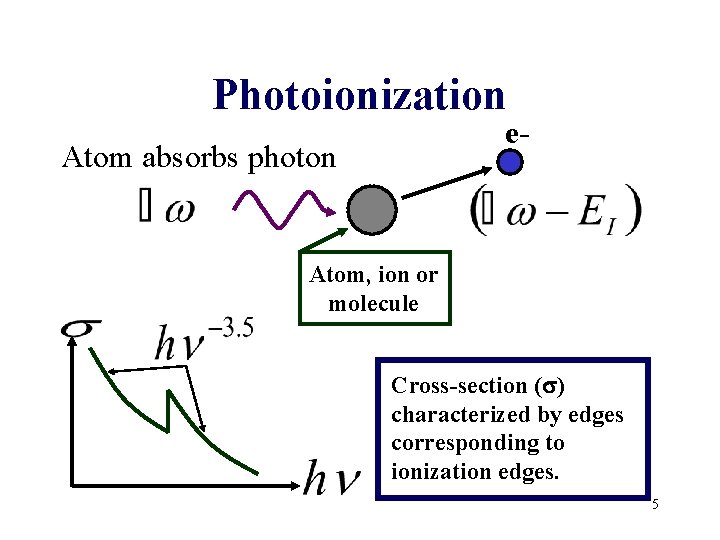
Photoionization e- Atom absorbs photon Atom, ion or molecule Cross-section (s) characterized by edges corresponding to ionization edges. 5

Photoelectric Absorption Cross-section The photoelectric absorption cross-section for photons with En > EI and hn << mec 2 is given by s. K = 4√ 2 s. T a 4 Z 5 (moc 2/n)7/2 where EI is the electron binding energy, a is the fine structure constant and s. T is the Thomson cross-section Note dependence on Z 5 and on n-7/2 6

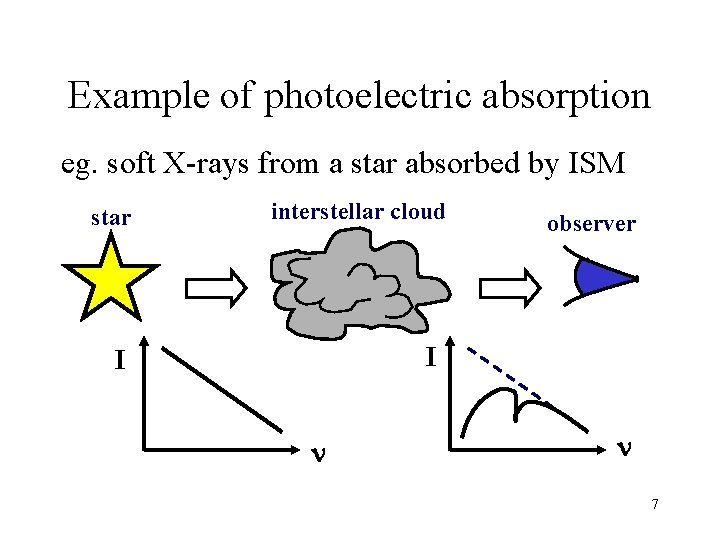
Example of photoelectric absorption eg. soft X-rays from a star absorbed by ISM star interstellar cloud observer I I n n 7

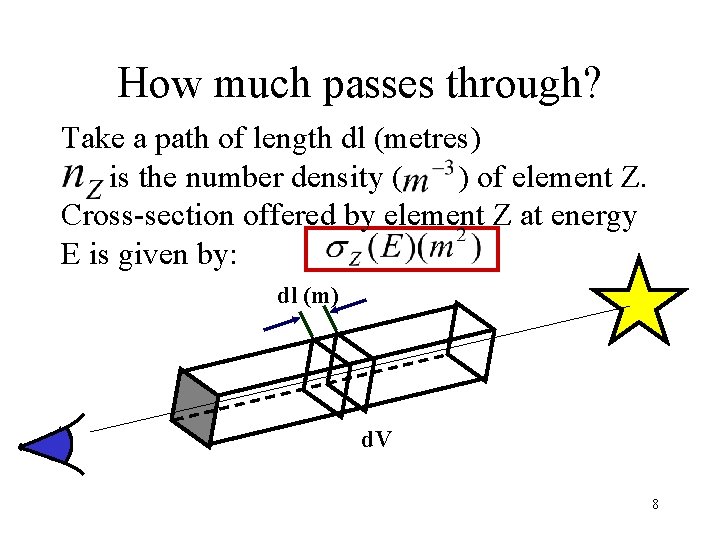
How much passes through? Take a path of length dl (metres) is the number density ( ) of element Z. Cross-section offered by element Z at energy E is given by: dl (m) d. V 8

The fraction of volume d. V which is blocked by the presence of element Z is : Thus fraction of flux F lost in volume d. V is: or : 9

Integrating over length from source. . . Including all elements in the line of sight: 10

Optical depth This becomes: This is ‘t’, the optical depth, which has no dimensions This is the effective cross-section, weighted over the abundance of elements with respect to hydrogen 11

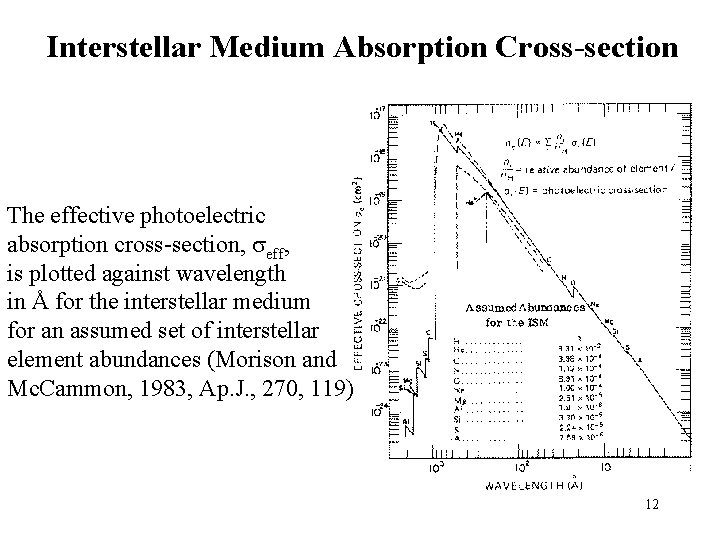
Interstellar Medium Absorption Cross-section The effective photoelectric absorption cross-section, seff, is plotted against wavelength in Å for the interstellar medium for an assumed set of interstellar element abundances (Morison and Mc. Cammon, 1983, Ap. J. , 270, 119) 12

Column density The column density given by : is the number of H – atoms per m 2 column Column density is measured from the 21 cm atomic hydrogen line - but not foolproof. There is a factor of 2 uncertainty, wide beams, molecular hydrogen contamination. . . 13

Clumping of the ISM Take an example at low energies, e. g. at Average ISM density At a distance, d=100 pc 14

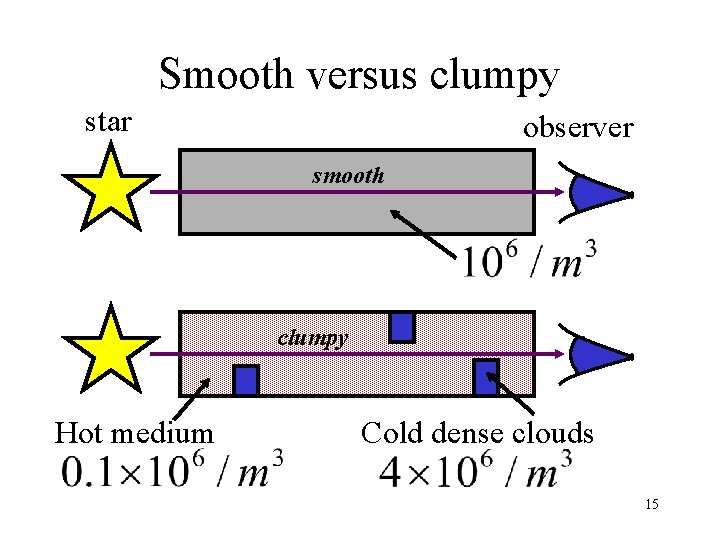
Smooth versus clumpy star observer smooth clumpy Hot medium Cold dense clouds 15

Numerical example • Through the smooth medium - • Through the clumpy medium - 16

Electron scattering • Thomson scattering - the scattering of a photon by an electron where the photon energy is much less than the rest mass of the electron. • Compton scattering - photons have a much higher energy in this case and lose some of their energy in the scattering process. 17

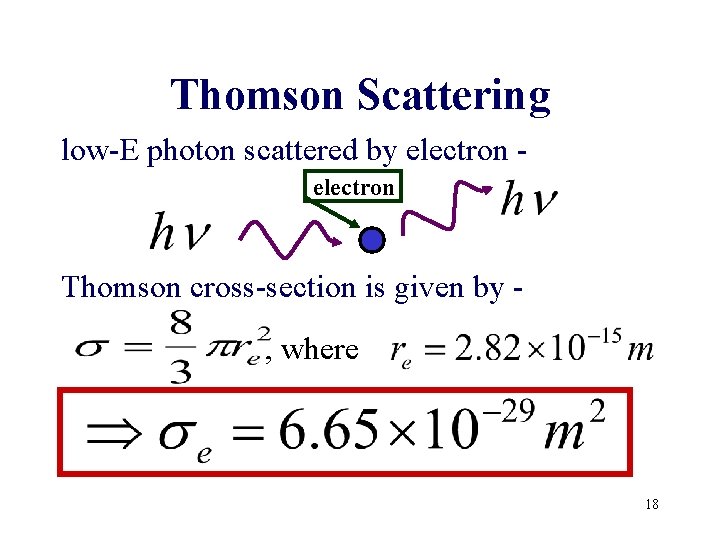
Thomson Scattering low-E photon scattered by electron Thomson cross-section is given by , where 18

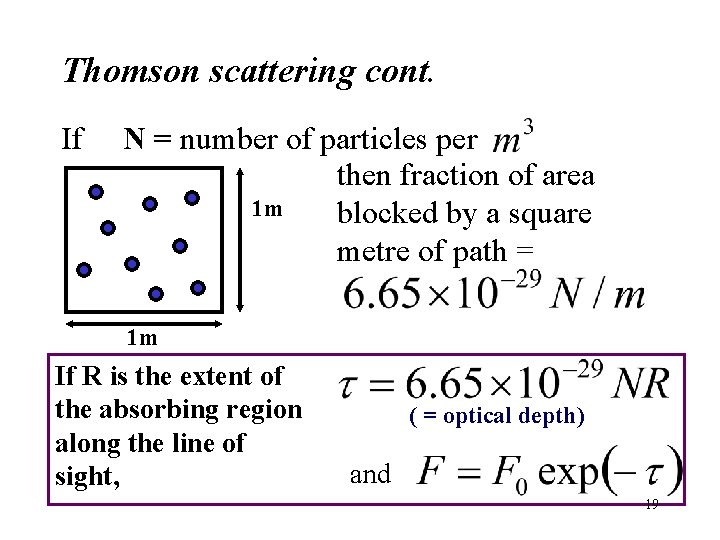
Thomson scattering cont. If N = number of particles per then fraction of area 1 m blocked by a square metre of path = 1 m If R is the extent of the absorbing region along the line of sight, ( = optical depth) and 19

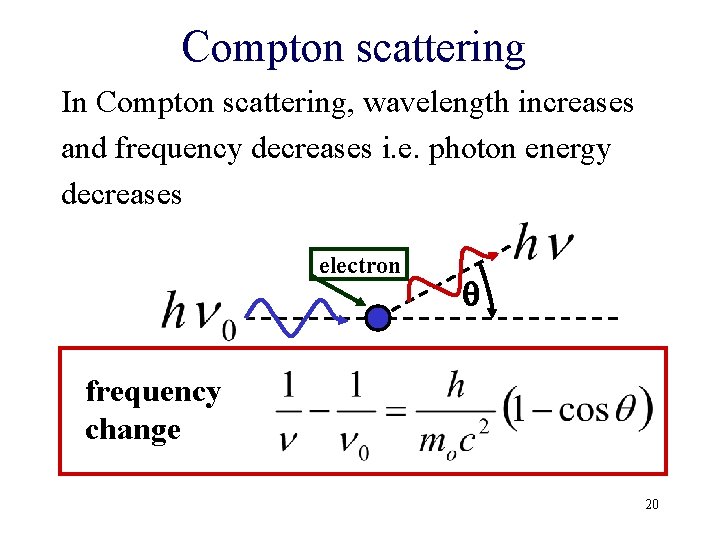
Compton scattering In Compton scattering, wavelength increases and frequency decreases i. e. photon energy decreases electron q frequency change 20

Compton scattering (cont. ) On average, 21

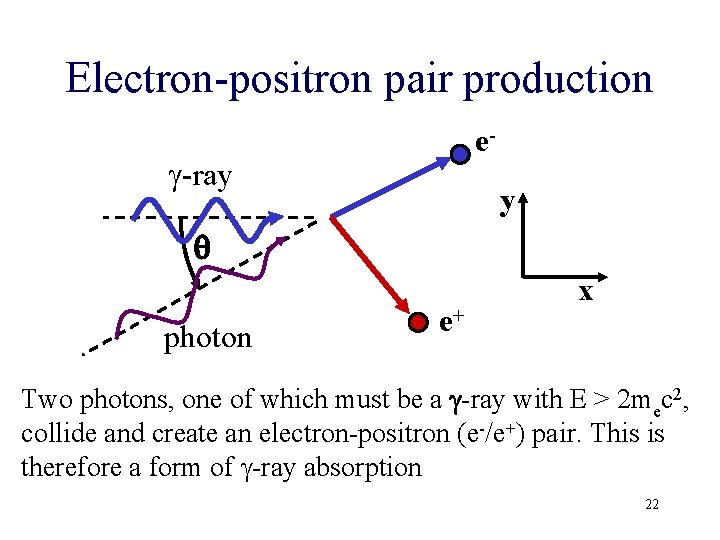
Electron-positron pair production e- g-ray y q photon e+ x Two photons, one of which must be a g-ray with E > 2 mec 2, collide and create an electron-positron (e-/e+) pair. This is therefore a form of g-ray absorption 22

Minimum g-ray energy required Must first demonstrate that relativistic invariant. is a Rest energy of particle, 23

Thus, from and , And this is a relativistic invariant 24
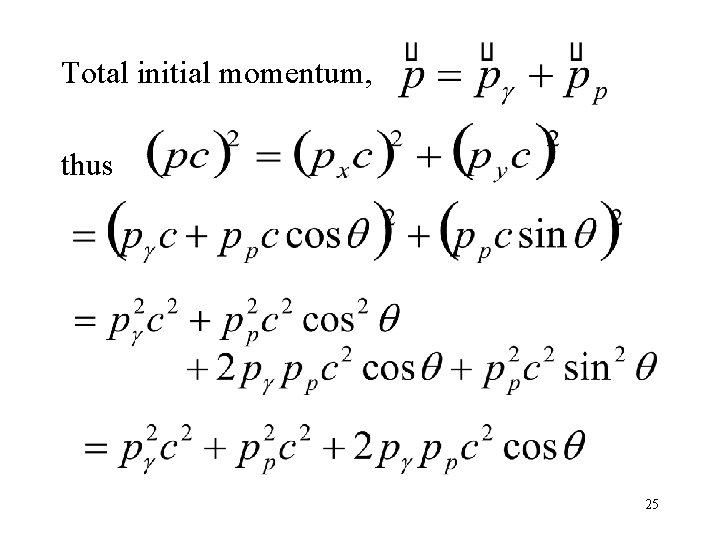
Total initial momentum, thus 25
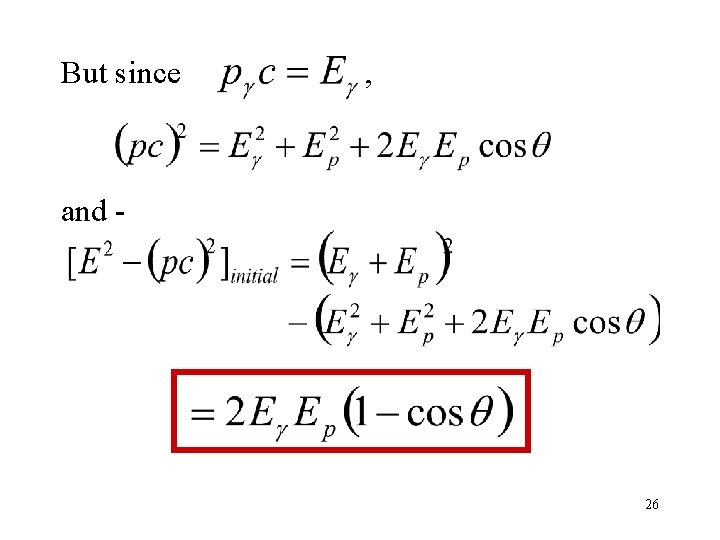
But since , and - 26

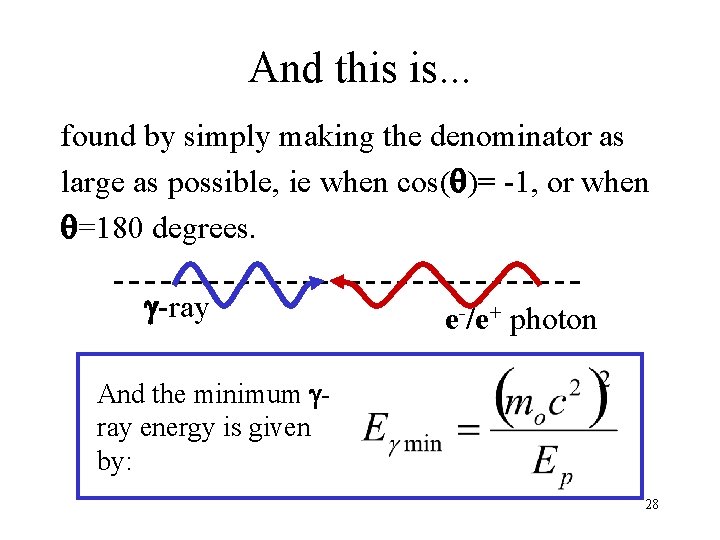
Calculating the minimum energy Assuming e+ and e- have no momentum… and since , Which gives us this expression for the energy of the g-ray photon 27

And this is. . . found by simply making the denominator as large as possible, ie when cos(q)= -1, or when q=180 degrees. g-ray e-/e+ photon And the minimum gray energy is given by: 28

Photon-nucleus pair production • In the laboratory, it is more usual to consider photon-nucleus production. So why do we ignore it in space? • Photons and nuclei have a similar crosssection, and the g-ray does not differentiate much between another photon or a nucleus. • Then we must compare the photon density with the particle density in space. 29

Photon versus particle density e. g. for 3 K m-wave background photons - Corresponding to about 109 photons / m 3 6 No of nuclei in space is about 10 / m 3 30

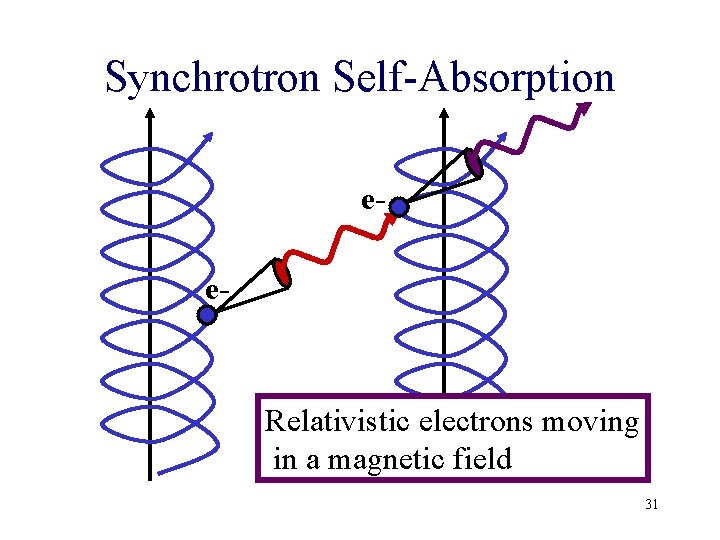
Synchrotron Self-Absorption ee- Relativistic electrons moving in a magnetic field 31

Synchrotron Emission Electrons, mainly responsible for emission at frequency n, have energy, E, given by: and for a power law electron spectrum log. Fn logn 32

Blackbody turnover Assume Synchrotron power-law cut off, nmax, is given by: and assume each electron emits and absorbs only at this peak frequency. Then, we will replace this with the mean energy per particle for a thermal source or E ~ k. T 33

On the Rayleigh-Jeans side. . . impossible log. Fn R-J blackbody synchrotron logn Rayleigh-Jeans approximation to blackbody. . . 34

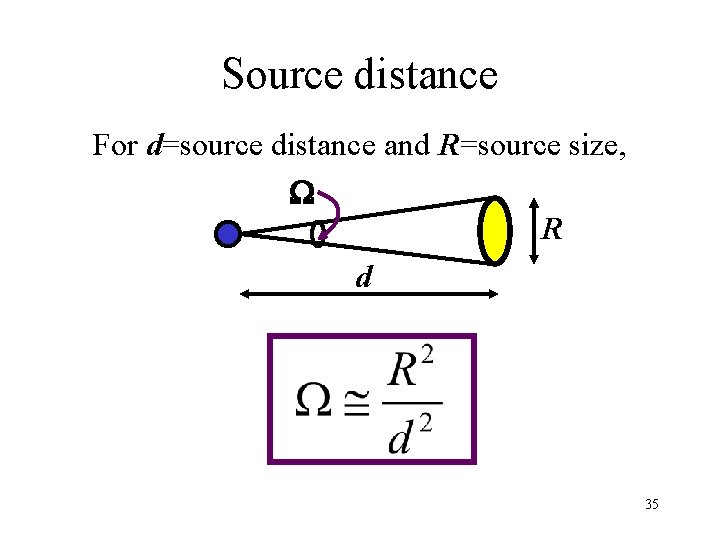
Source distance For d=source distance and R=source size, W R d 35

Total flux at Earth. . . So total energy flux at Earth is given by: 36

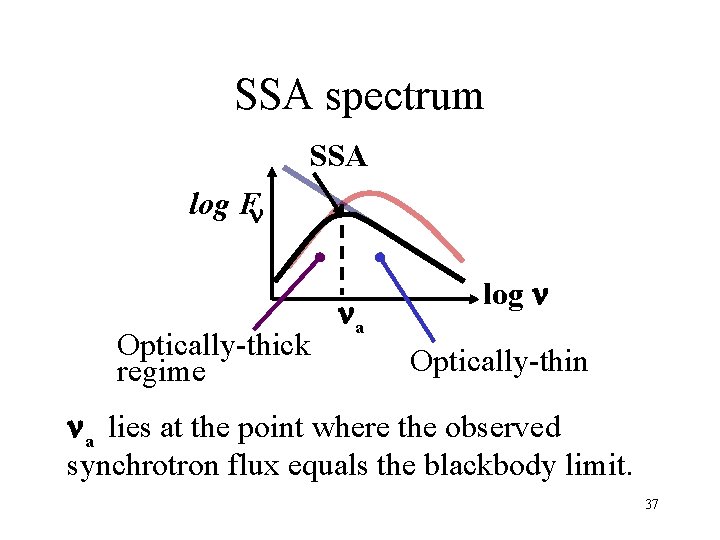
SSA spectrum SSA log Fn Optically-thick regime na log n Optically-thin n a lies at the point where the observed synchrotron flux equals the blackbody limit. 37

… and SSA frequency Substituting for W then: and 38

SSA in Compact X-ray sources X-ray frequency, n=1018 Hz -29 If Fn ~ 10 J m-2 s-1 Hz - typical X-ray source value d = 10 kpc and B = 108 Tesla (the field for a neutron star) This gives a maximum for R of ~1 km for SSA of X -rays to occur (ie for n to a be observable in the Xray band). but a neutron star diameter is 10 to 20 km 39

Radiation processes (summary) • Thermal - Bremsstrahlung electron energies ~ photon energies to produce X-rays, b = v/c ~ 0. 1 • Non-thermal - Synchrotron and Inverse Compton 40

Synchrotron Emission For an electron spiralling in a magnetic field B with energy E, the peak radiated frequency, nm is nm = g 2 B e/2 p mo = E 2 B e/2 p mo 3 c 4 But Hence E = g mo c 2 - for a relativistic electron g 2 = 2 p mo nm/B e 41

Electron energies required • Synchrotron emission depends on the magnetic field strength. Assuming equipartition of energy - starlight, cosmic rays + magnetic fields have all the same energy density in Galaxy and from To produce X-rays of -10 , => B=6 x 10 Tesla nm ~ 1018 Hz, we need 42

Inverse Compton Scattering For a relativistic electron colliding with a low energy photon, g. IC 2 ≈ hnfinal/hninitial For X-ray production consider: - starlight: <hn> ~ 2 e. V (l~6000 A) -4 - 3 K background: <hn> ~3 x 10 e. V then = = for stars for the 3 K background We need cosmic rays!!! 43

RADIATION PROCESSES END OF TOPIC 44