Radiation Processes High Energy Astrophysics empmssl ucl ac














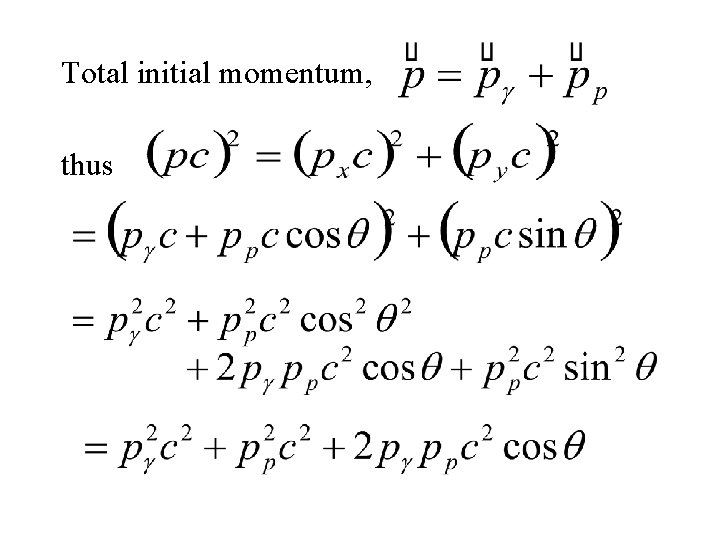
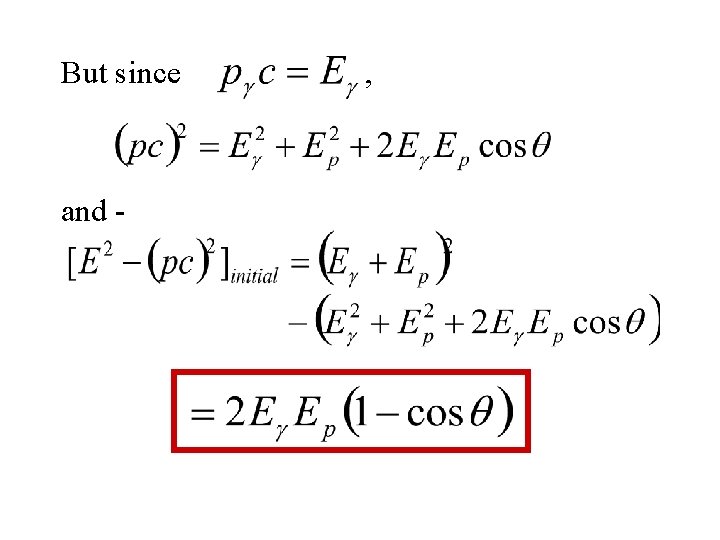





















- Slides: 48

Radiation Processes High Energy Astrophysics emp@mssl. ucl. ac. uk http: //www. mssl. ucl. ac. uk/

Absorption Processes So far, considered the production of X-rays. Now, will consider X-ray absorption. Emission processes Recombination Absorption process Photoionization Inverse Compton electron scattering e-/p+ annihilation e-/p+ pair production synchrotron emission synchrotron self absorption

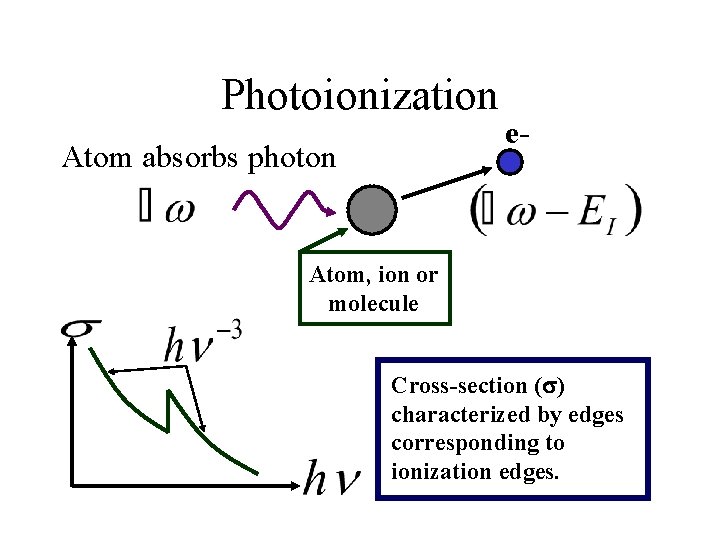
Photoionization Atom absorbs photon e- Atom, ion or molecule Cross-section (s) characterized by edges corresponding to ionization edges.

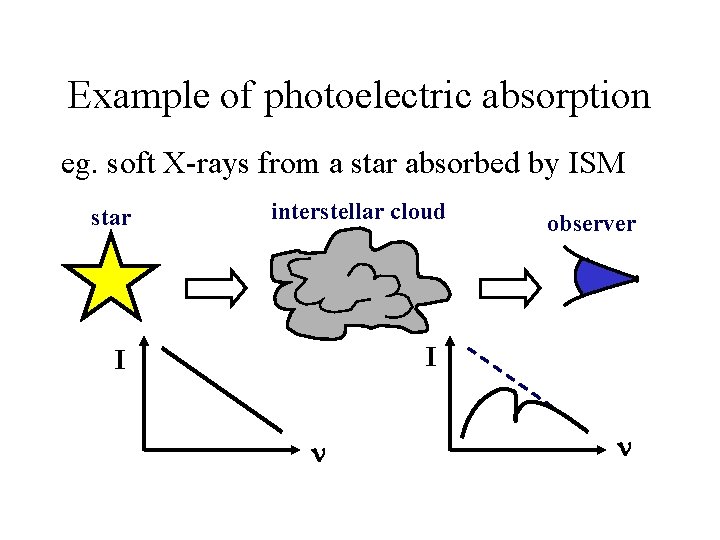
Example of photoelectric absorption eg. soft X-rays from a star absorbed by ISM star interstellar cloud observer I I n n

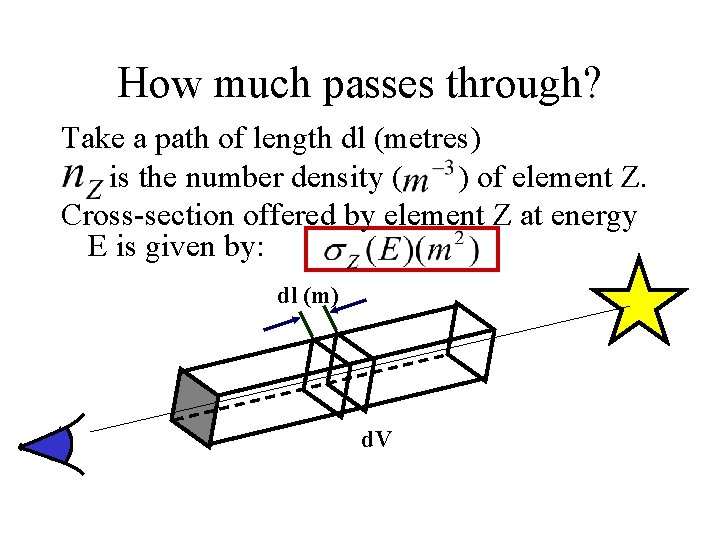
How much passes through? Take a path of length dl (metres) is the number density ( ) of element Z. Cross-section offered by element Z at energy E is given by: dl (m) d. V

The fraction of volume d. V which is blocked by the presence of element Z is : Thus the fraction of flux lost in volume d. V is: or :

Integrating over length from source. . . Including all elements in the line of sight:

Optical depth This becomes: This is ‘t’, the optical depth, which has no dimensions This is the effective cross-section, weighted over the abundance of elements with respect to hydrogen

Column density The column density is given by : Column density is measured from the 21 cm atomic hydrogen line - but not foolproof. There is a factor of 2 uncertainty, wide beams, molecular hydrogen contamination. . .

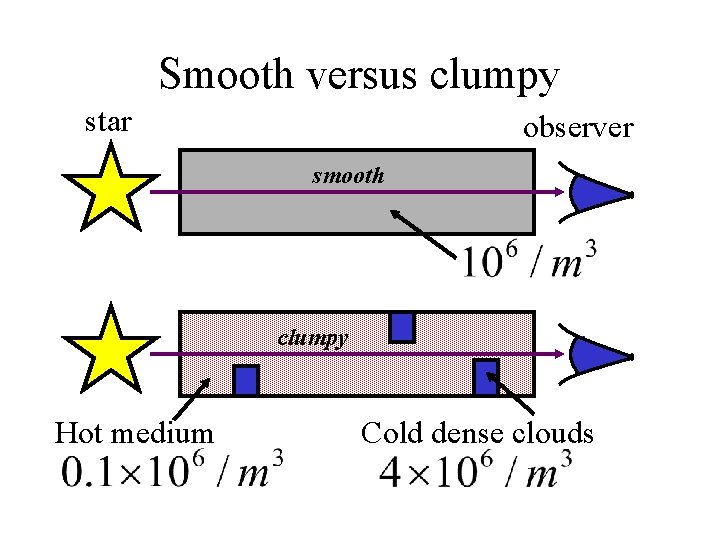
Clumping of the ISM Take an example at low energies, eg at. . . Average ISM density At a distance, d=100 pc

Smooth versus clumpy star observer smooth clumpy Hot medium Cold dense clouds

Numerical example • Through the smooth medium - • Through the clumpy medium -

Electron scattering • Thomson scattering - the scattering of a photon by an electron where the photon energy is much less than the rest mass of the electron. • Compton scattering - photons have a much higher energy in this case and lose some of their energy in the scattering process.

Thomson Scattering low-E photon scattered by electron Thomson cross-section is given by , where

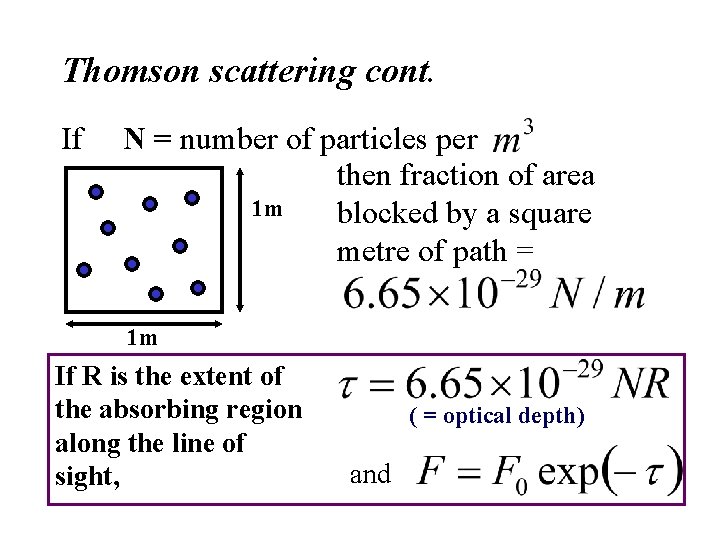
Thomson scattering cont. If N = number of particles per then fraction of area 1 m blocked by a square metre of path = 1 m If R is the extent of the absorbing region along the line of sight, ( = optical depth) and

Compton scattering In Compton scattering, the photon wavelength increases, ie its energy decreases. electron frequency change q

Compton scattering cont. On average,

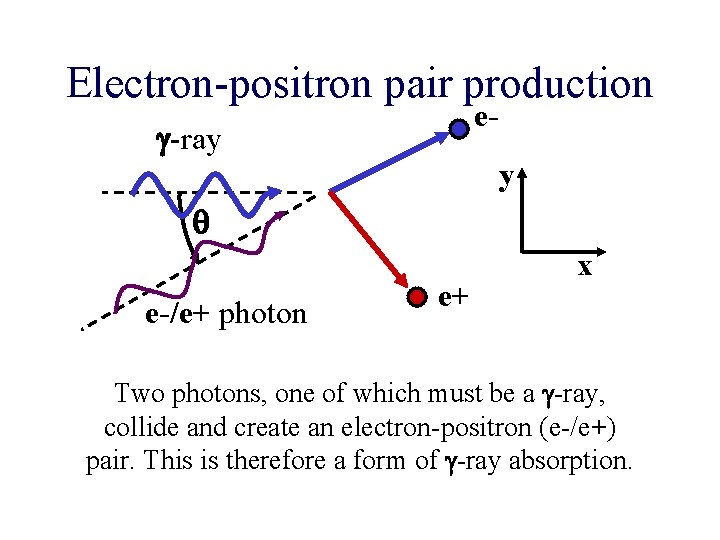
Electron-positron pair production e- g-ray y q e-/e+ photon e+ x Two photons, one of which must be a g-ray, collide and create an electron-positron (e-/e+) pair. This is therefore a form of g-ray absorption.

Minimum g-ray energy required Must first demonstrate that relativistic invariant. Rest energy of particle, is a

Thus, from and , And this is a relativistic invariant
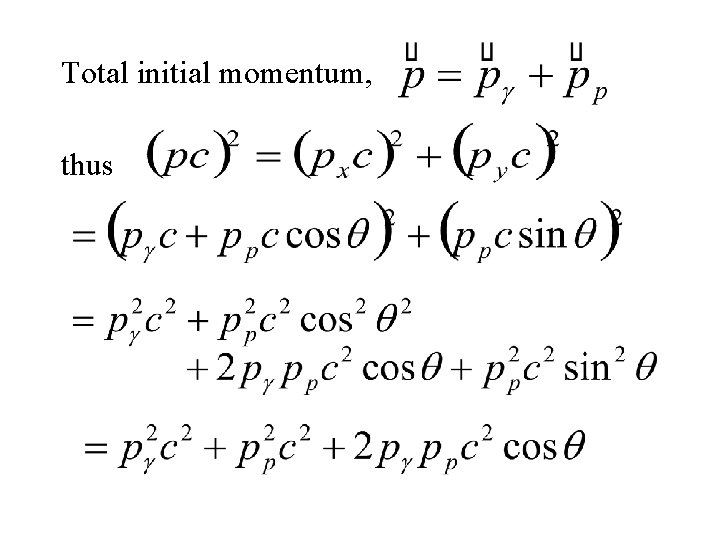
Total initial momentum, thus
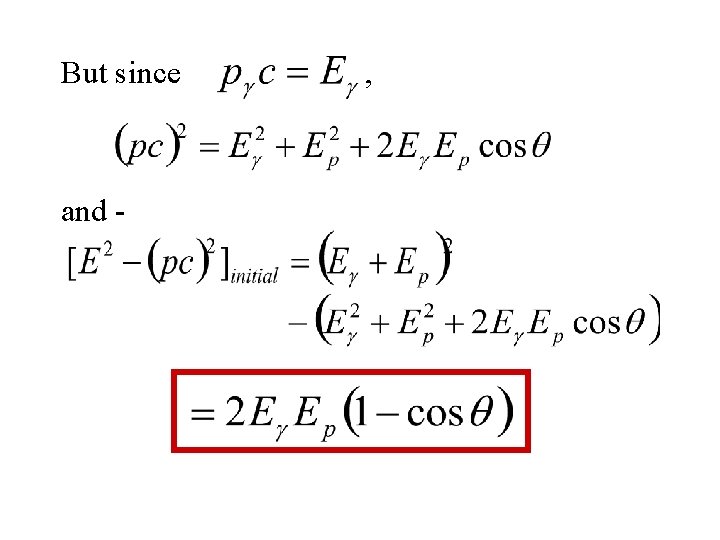
But since and - ,

Calculating the minimum energy Assuming e+ and e- have no momentum… and since Which gives us this expression for the energy of the g-ray photon ,

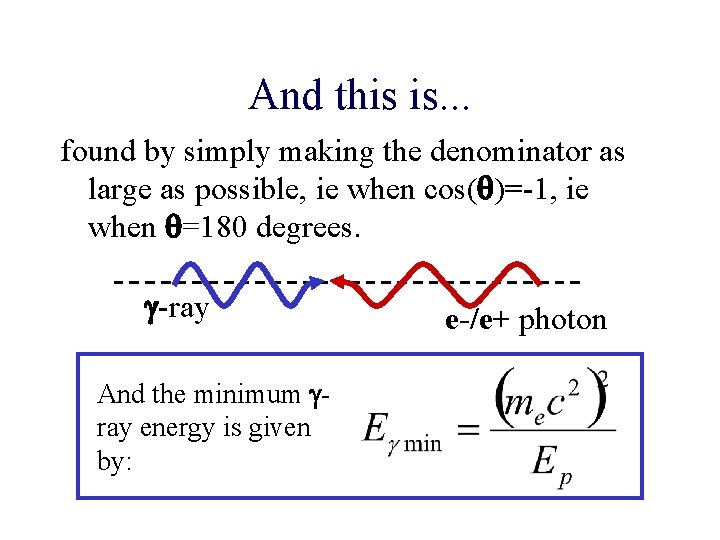
And this is. . . found by simply making the denominator as large as possible, ie when cos(q)=-1, ie when q=180 degrees. g-ray And the minimum gray energy is given by: e-/e+ photon

Minimum energy for mm-wave photon g-ray photon interacts with mm-wave First converting to e. V : -3 l=1. 2 mm corresponds to hn=10 e. V

Photon-nucleus pair production • In the laboratory, it is more usual to consider photon-nucleus production. So why do we ignore it in space? • Photons and nuclei have a similar crosssection, and the g-ray does not differentiate much between another photon or a nucleus. • Then we must compare the photon density with the particle density in space.

Photon versus particle density eg. , for 3 K m-wave background photons - Corresponding to about 109 photons / m 3 6 No of nuclei in space is about 10 / m 3

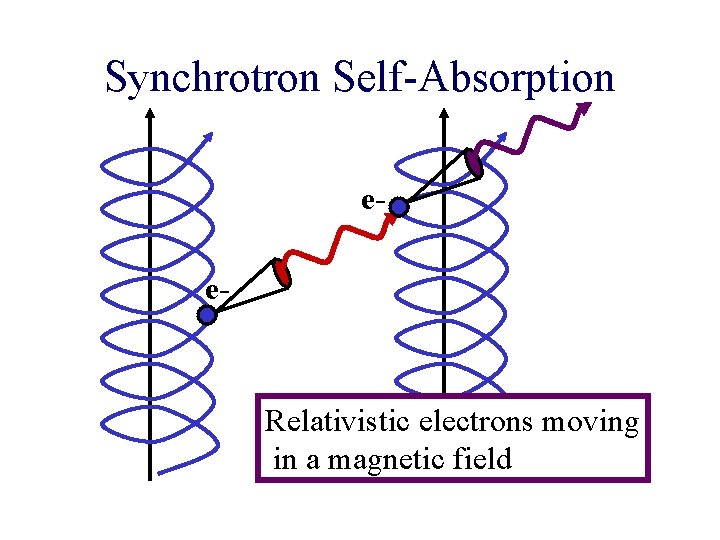
Synchrotron Self-Absorption ee- Relativistic electrons moving in a magnetic field

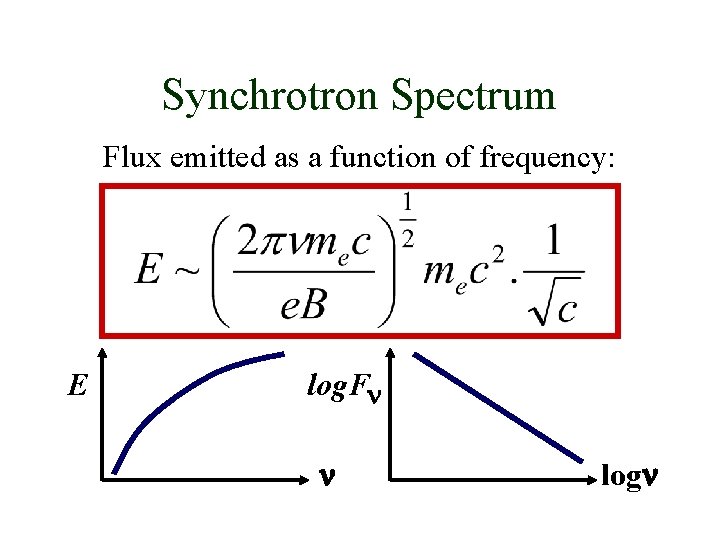
Synchrotron Spectrum Flux emitted as a function of frequency: E log. Fn n logn

Blackbody turnover Assume power-law cut off, nmax, is given by: And assume each electron emits & absorbs only at this peak frequency. Then, we will replace this with the mean energy per particle for a thermal source, ~k. T.

On the Rayleigh-Jeans side. . . impossible log. Fn R-J blackbody synchrotron logn Rayleigh-Jeans approximation to blackbody. . .

Total flux at Earth. . . So total energy flux at Earth is given by:

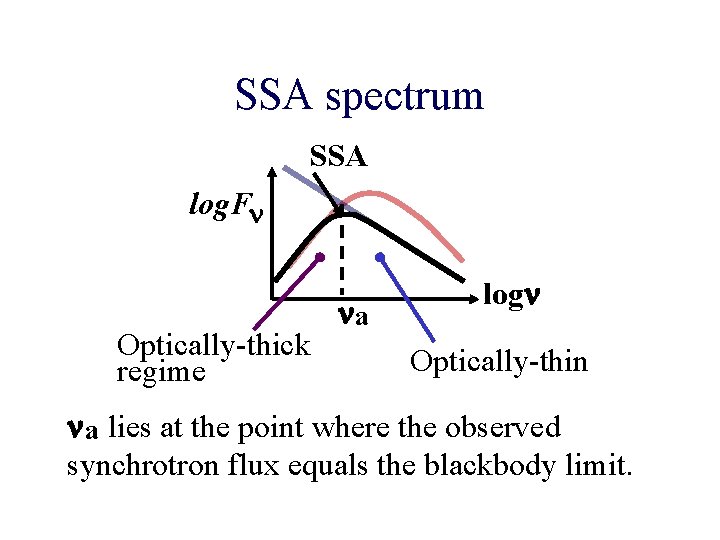
SSA spectrum SSA log. Fn Optically-thick regime na logn Optically-thin n a lies at the point where the observed synchrotron flux equals the blackbody limit.

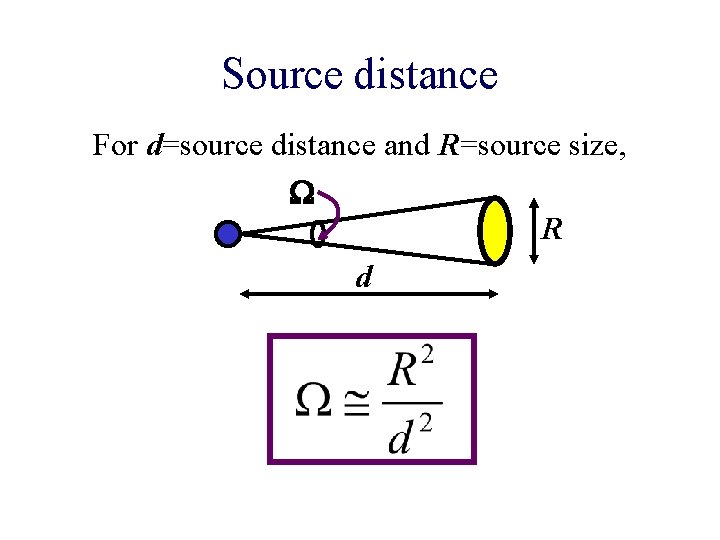
Source distance For d=source distance and R=source size, W R d

… and SSA frequency Substituting for W then: and

SSA in Compact X-ray sources X-ray frequency, n=10 18 Hz Assume Fn ~ 10 -29 J m-2 s -1 Hz d = 10 kpc and B = 10 8 Tesla (the field for a neutron star) This gives a maximum for R of ~1 km for SSA of X-rays to occur (ie for na to be observable in the X-ray band). - but a neutron star diameter is 10 to 20 km -

Radiation processes (summary) • Thermal - Bremsstrahlung electron energies ~ photon energies to produce X-rays, b = v/c ~ 0. 1 • Non-thermal - Synchrotron and Inverse Compton

Electron energies required • Synchrotron emission depends on the magnetic field strength assuming equipartition of energy starlight, cosmic rays + magnetic fields have all the same energy density in Galaxy • from To produce X-rays, , => B=6 x 10 -10 Tesla

Inverse Compton Scattering Consider starlight: <hn> ~ 2 e. V (l~6000 A) or 3 K background photons, <hn> ~3 x 10 -4 e. V then = for stars = for the 3 K background, to produce X-rays. We need cosmic rays!!!

Non-thermal process (cont. ) Energy distribution of cosmic ray particles within a unit volume has the form: (over at least part of the energy range) We use this to determine the relative importance of synchrotron and IC processes

Power radiated in the two processes is about equal in the case of equipartition of energy ie when ie an electron with a given g loses energy equally rapidly by the two processes However, it does not mean that X-rays are produced at the same rate in the two cases.

Ratio of IC to Synchrotron Xrays For example: Galactic X-rays require (stars) (3 K) but for synchrotron

Ratio IC to Synchrotron (cont. ) Ratio = (no of electrons with But: ) )

Ratio IC to Synchrotron (cont. ) Thus: So which is more important for producing X-rays via IC; starlight or 3 K background?

X-rays from IC scattering (no. X-rays produced from starlight per (no. X-rays produced from 3 K per ) )

IC - starlight versus 3 K We know that and Thus ie 3 K photons more important!

IC or synchrotron for X-rays? Remember assuming for : thus synchrotron dominates over IC in Galaxy

Synchrotron emission requires very high energy particles however - and electron energy distribution may well have tailed off if there is no continuous re-supply. Also 3 K radiation extends outside our Galaxy. Extragalactic radiation depends on whethere are enough electrons to produce IC.