Radians These are the Trigonometric graphs but with

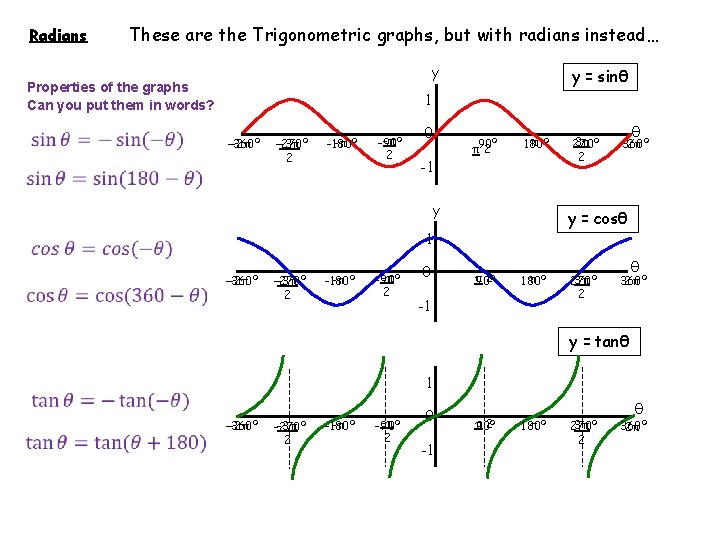
Radians These are the Trigonometric graphs, but with radians instead… y Properties of the graphs Can you put them in words? y = sinθ 1 -2π -360º -3π -270º 2 -π -180º -π -90º 2 0 -1 π90º 2 π 180º y -2π -360º -3π -270º 2 -π -90º 2 0 θ 360º 2π y = cosθ 1 -π -180º 3π 270º 2 π 2 90º π 180º -1 3π 270º 2 θ 360º 2π y = tanθ 1 -2π -360º -3π -270º 2 -π -180º -π -90º 2 0 -1 π 2 90º π 180º 3π 270º 2 θ 360º 2π

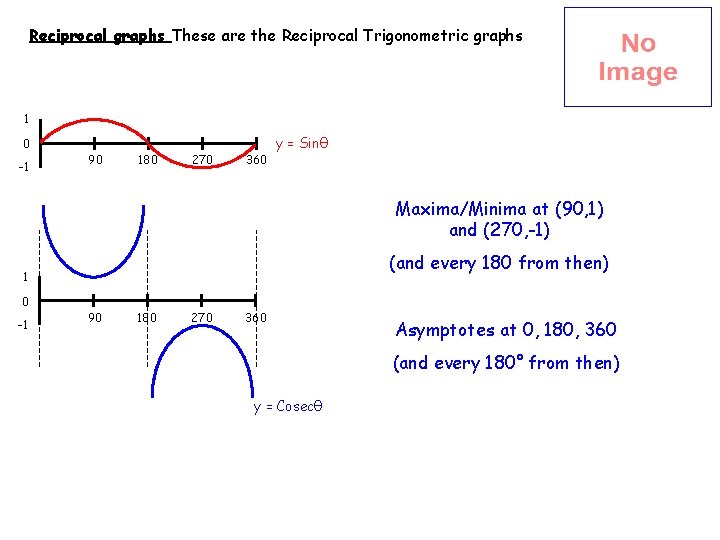
Reciprocal graphs These are the Reciprocal Trigonometric graphs 1 0 -1 90 180 270 360 y = Sinθ Maxima/Minima at (90, 1) and (270, -1) (and every 180 from then) 1 0 -1 90 180 270 360 Asymptotes at 0, 180, 360 (and every 180° from then) y = Cosecθ

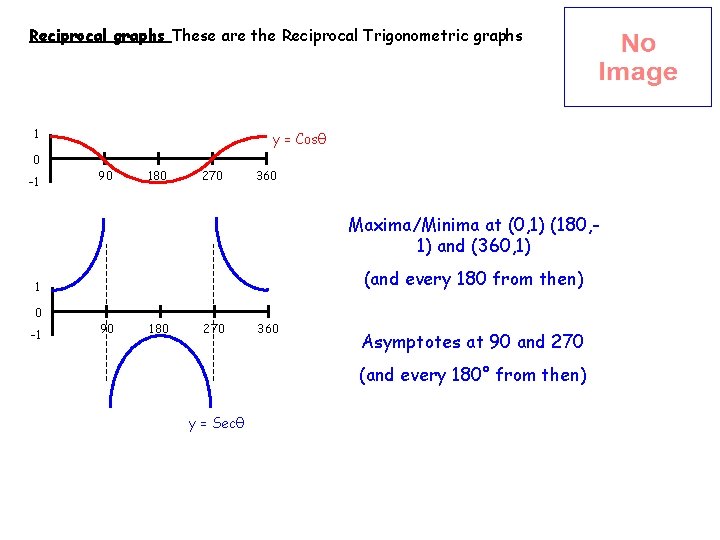
Reciprocal graphs These are the Reciprocal Trigonometric graphs 1 0 -1 y = Cosθ 90 180 270 360 Maxima/Minima at (0, 1) (180, 1) and (360, 1) (and every 180 from then) 1 0 -1 90 180 270 360 Asymptotes at 90 and 270 (and every 180° from then) y = Secθ

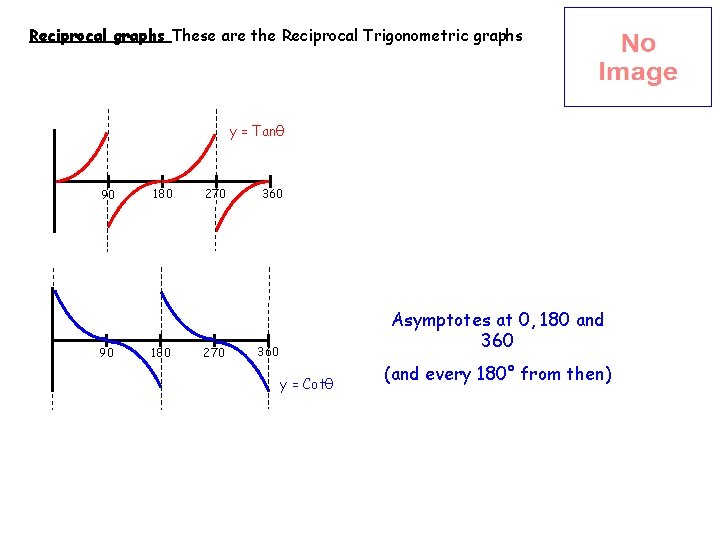
Reciprocal graphs These are the Reciprocal Trigonometric graphs y = Tanθ 90 90 180 270 360 Asymptotes at 0, 180 and 360 y = Cotθ (and every 180° from then)

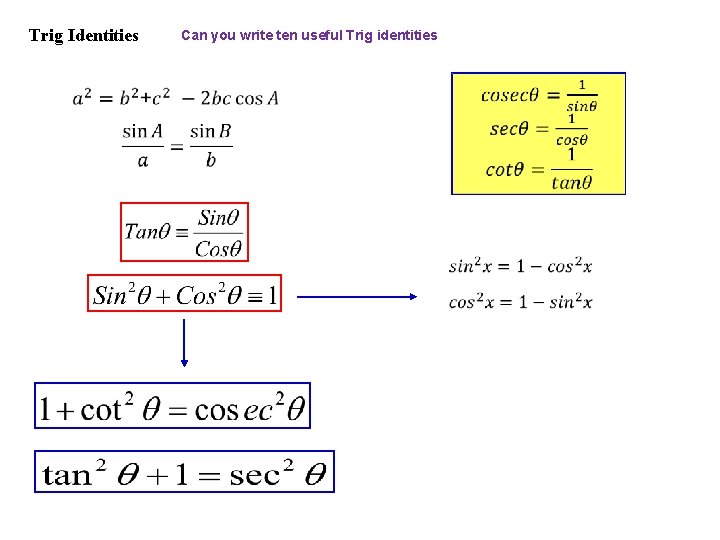
Trig Identities Can you write ten useful Trig identities

Trig Identities Can you write ten useful Trig identities Formula booklet

SOLUTION and MARKSCHEME

SOLUTION and MARKSCHEME

END