Radians Ratios Primary Reciprocal Scenarios 100 100 100































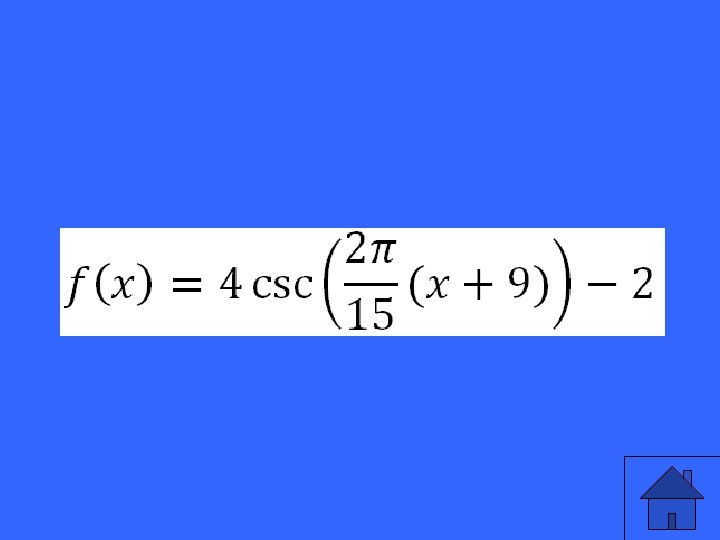


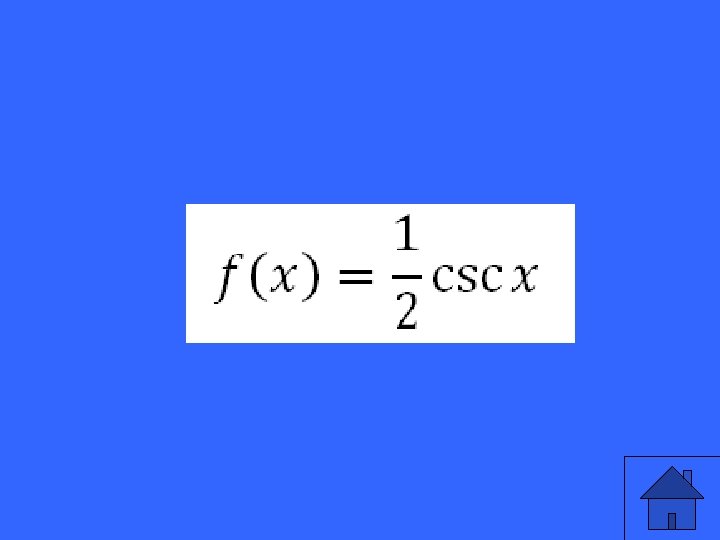

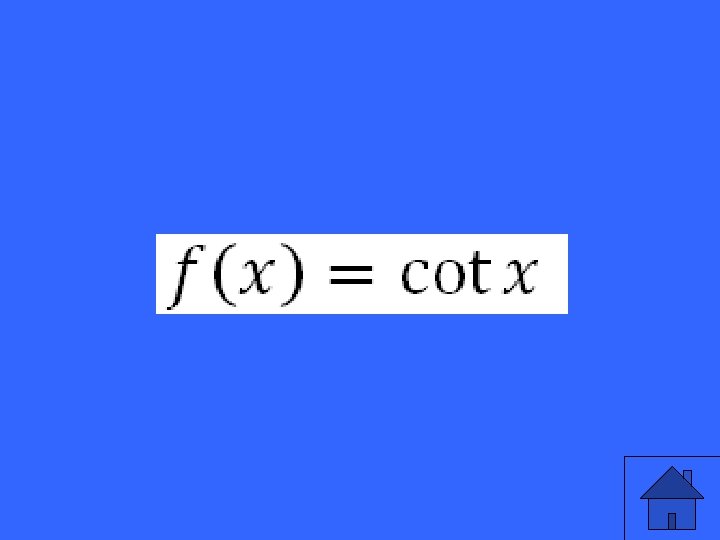

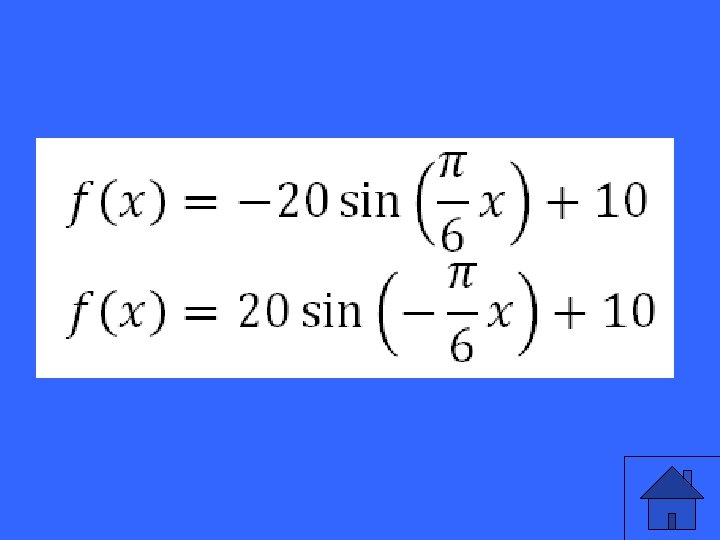

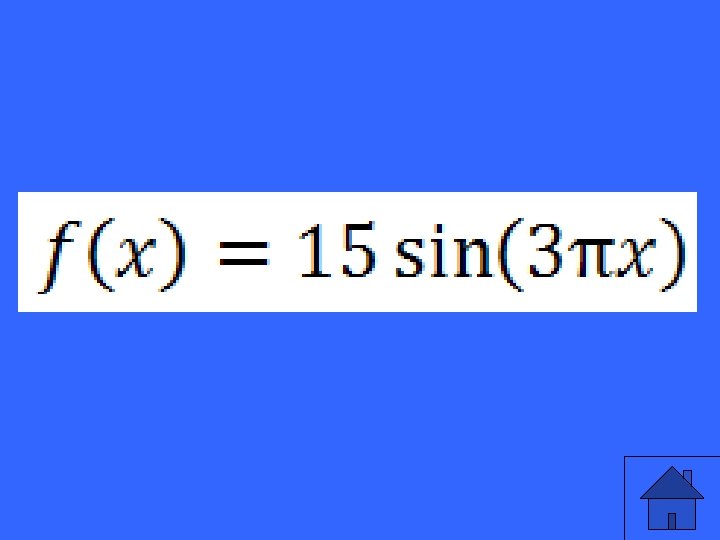





- Slides: 51

Radians Ratios Primary Reciprocal Scenarios 100 100 100 200 200 200 300 300 300 400 400 400 500 500 500

Determine the exact o radian measure for 210


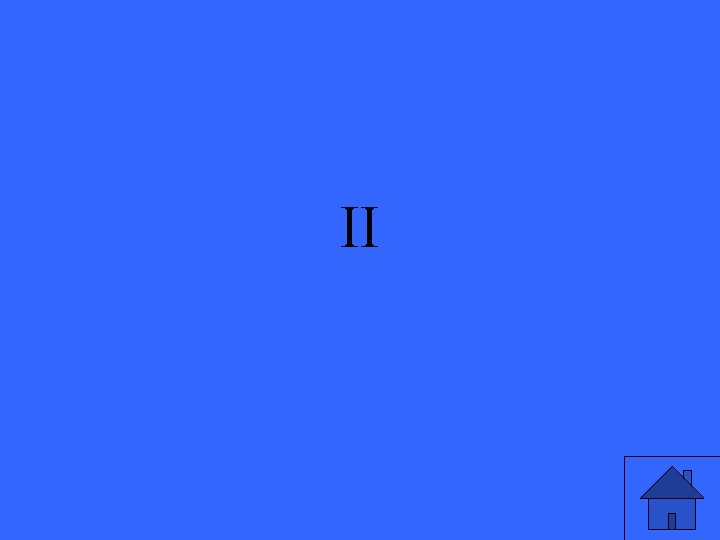
In which quadrant is 1. 7 radians?

II

Determine a radian measure for o -71 to two decimal places

-1. 24

A windmill turns 15 times in a minute. Determine the angular velocity in radians/second


Find the missing measurement

2. 9 cm

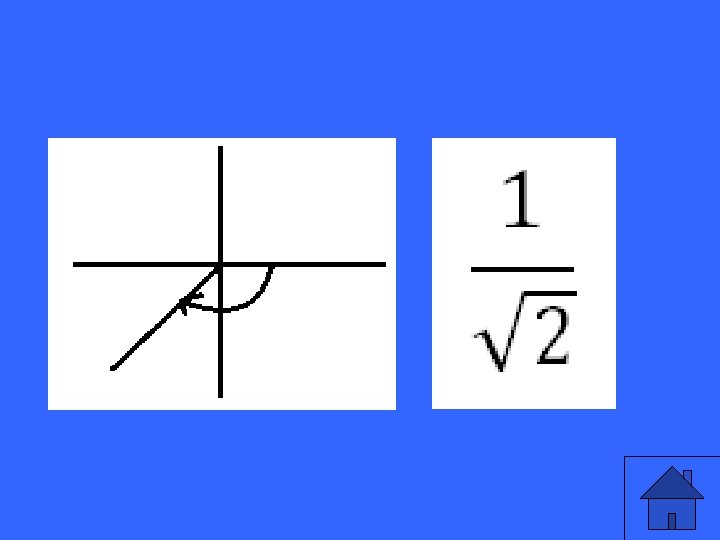
Sketch the angle in standard position and determine the exact value of the trig ratio:


If cos 0=fra determine tan 0

OR

Find the angle whose terminal arm goes through the point (2, -4)

5. 18 radians

State an equivalent expression in terms of the related acute angle


Find the exact radian measure of the angle whose terminal arm goes through (-17, -17)


Describe the transformations on the parent function to create the function

Vertical stretch by a factor of 2 Compression by a factor of (period is ) Phase shift right units Vertical shift up 7 units

Write the equation of the tan function described: Vert. Reflection Vert. Stretch by a factor of 5 Period of 5 units Phase Shift left 7 units Vertical Shift down 3 units


State the Domain, Range, Period, and Equation of the Axis for the function


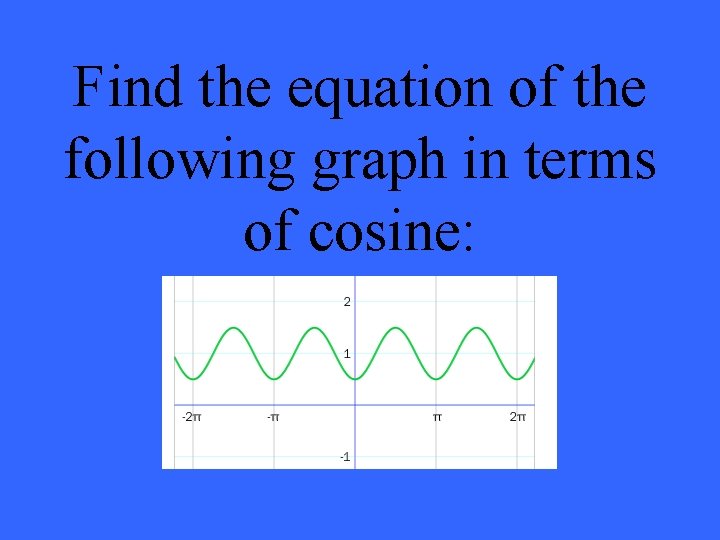
Find the equation of the following graph in terms of cosine:


Write the domain and range of the function f(x) = tan x


Describe the transformations on the parent function to create the function

Reflection across the x-axis Compression by a factor of Phase shift right units Vertical shift up 4 units

Write the equation of the csc function described: Vert. Stretch by a factor of 4 Period of 15 units Phase Shift left 9 units Vertical Shift down 2 units
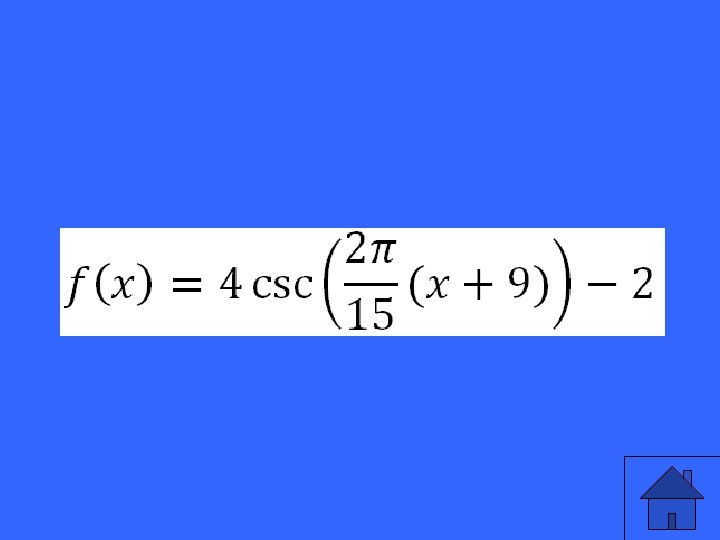

State the Domain, Range, Period, and Equation of the Axis for the function


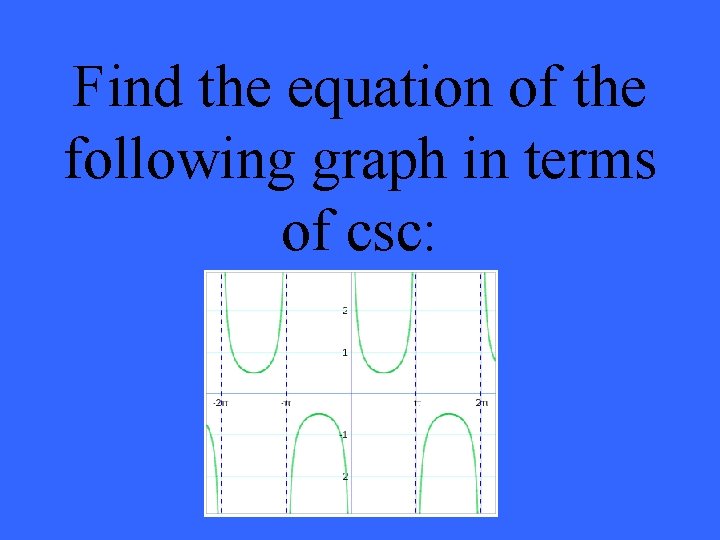
Find the equation of the following graph in terms of csc:
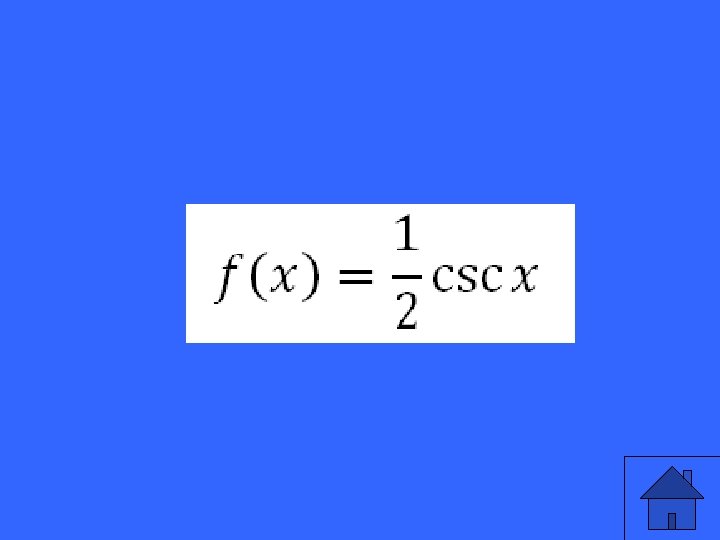

What is the only reciprocal trig function that can be written as a primary function transformed using our regular transformations?
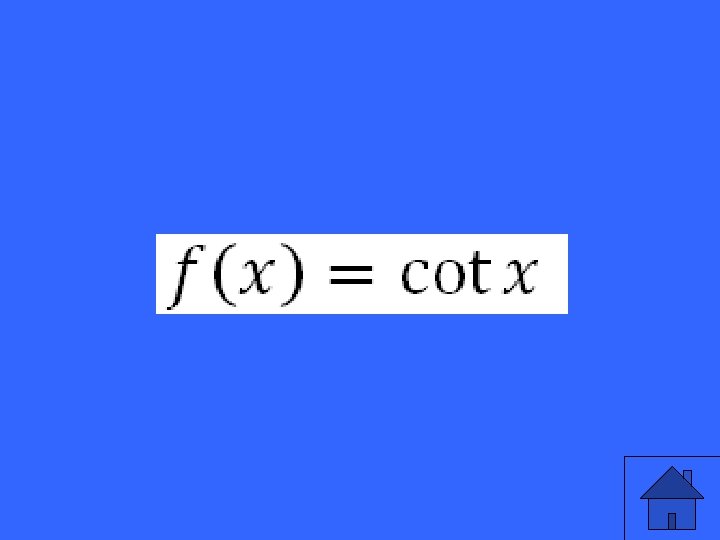

Write the equation matching the following description: -Max temperature is 30 o. C o -Min temperature is -10 C -Cycle repeats every 12 months -Start measurements at the average temperature after summer (temperature is dropping)
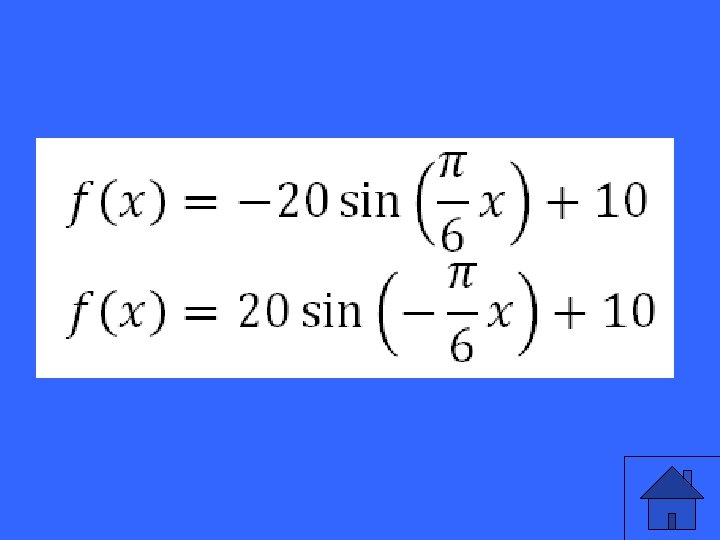

A pendulum swings 15 cm on either side from its starting place. It takes 8 seconds to complete 12 cycles. Write an equation to represent this scenario.
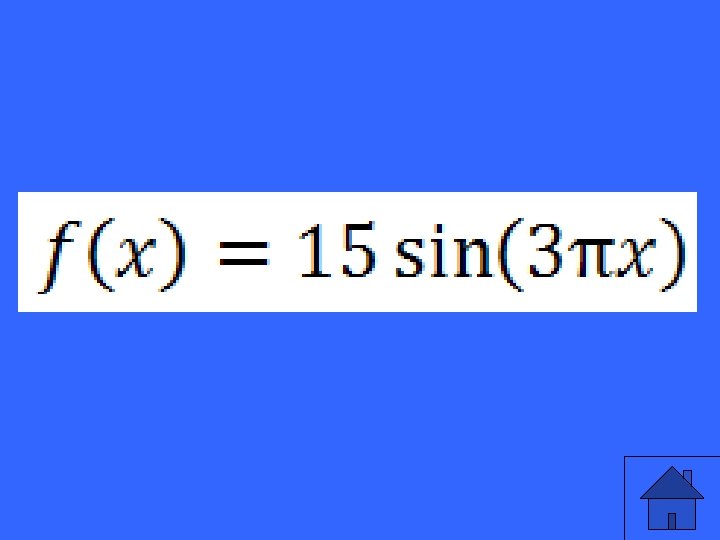

A Ferris wheel has a diameter of 25 m. The lowest point is 3 m above the ground, but riders get on at 6 m above the ground. It takes 4 minutes to return to the starting position. Find an equation to represent a rider’s height in metres after a certain amount of time in minutes.


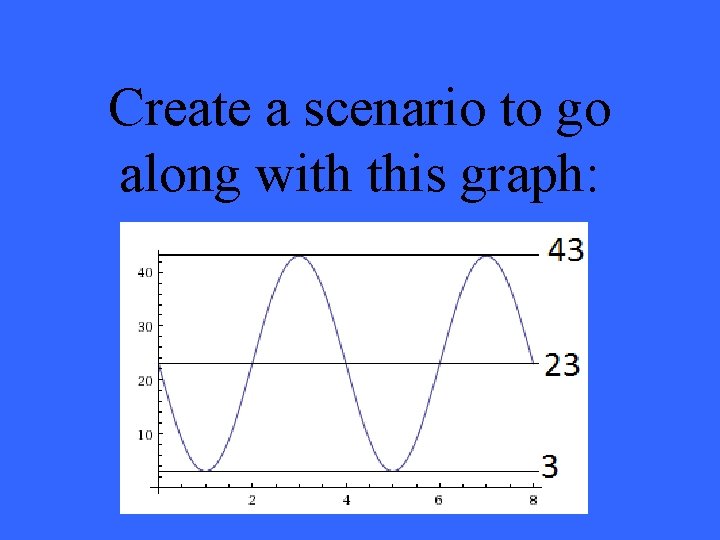
Create a scenario to go along with this graph:

Many different answers including: monthly patterns (every 4 weeks) spinning keys around, one cycle/4 seconds driving in a circular track- one lap takes 4 minutes etc.

I hope you pick this one last… (but you picked the highest value ones first last time, so you probably won’t)

GOOD LUCK