Radians Radian measure is an alternative to degrees

Radians Radian measure is an alternative to degrees and is based upon the ratio of al θ r θ- theta arc length (al) radius

θ al = r If the arc length = the radius r θ (radians) = r/r = 1 1 radian = 57∙ 3 o

● If we now take a semi-circle π radians al = 180 o Here al = ½ of Learn this!! circumference == ½ ½ of of 2πr πd θ r = πr So θ (radians) = πr /r = π

π (radians) = 180 o The connection between radians and degrees is : This now gives us 2π = 360 o π / = 90 o 3π / = 270 o 2 2 π/ 3 π/ 4 π/ 6 = 60 o = 45 o /3 = 120 o 3π / = 135 o 4 5π / = 150 o 6 2π = 30 o NB: Radians are usually expressed as fractional

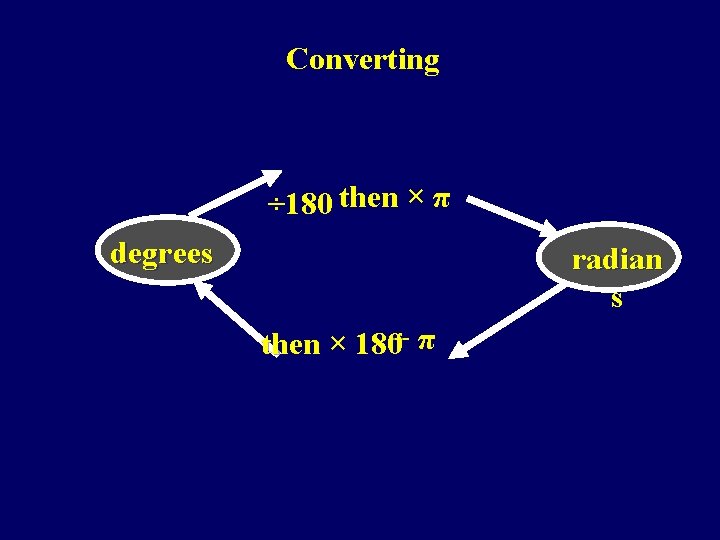
Converting ÷ 180 then × π degrees radian s then × 180÷ π

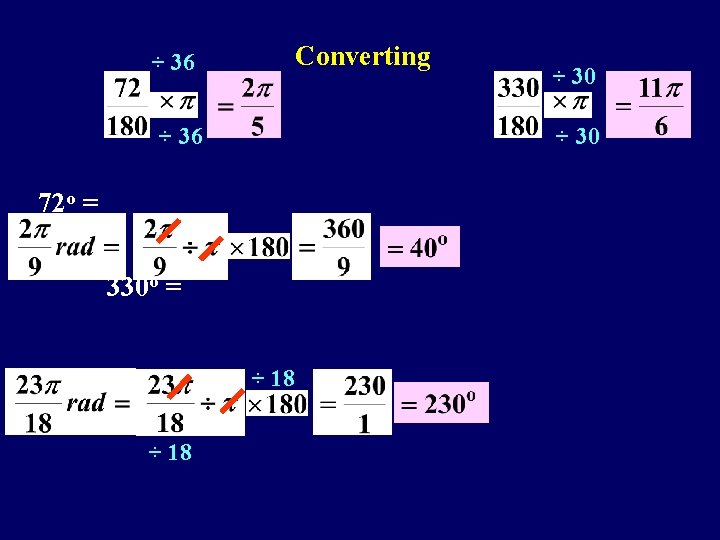
Converting ÷ 36 ÷ 30 ÷ 36 72 o = 330 o = ÷ 18 ÷ 30

Angular Velocity In the days before CDs the most popular format for music was “vinyls”. Singles played at 45 rpm while albums played at 331/3 rpm = revolutions per minute ! Going back about 70 years an earlier version of vinyls played at 78 rpm. Convert these record speeds into “radians per second

So So NB: 1 revolution = = 2π radians 1 min = 60 o secs 45 rpm 360 = 45 × 2π or 90π radians per min = 90π/60 or 3π/2 radians per sec 331/3 rpm = 331/3 × 2π or 662/3 π radians per min = 662/3 × π /60 or So 10 π / 9 radians per sec 78 rpm = 78 × 2π or 156π radians per min = 156π/ 60 or 13 π / sec 5 radians per

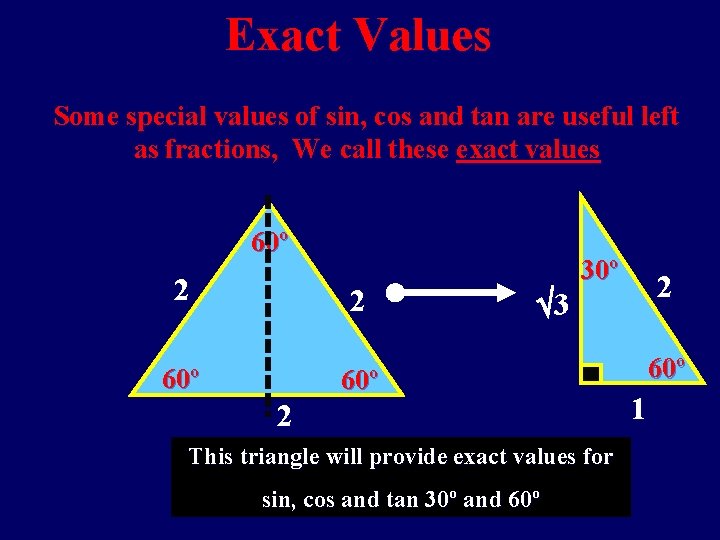
Exact Values Some special values of sin, cos and tan are useful left as fractions, We call these exact values 60º 2 2 60º 3 30º 2 This triangle will provide exact values for sin, cos and tan 30º and 60º 2 60º 1

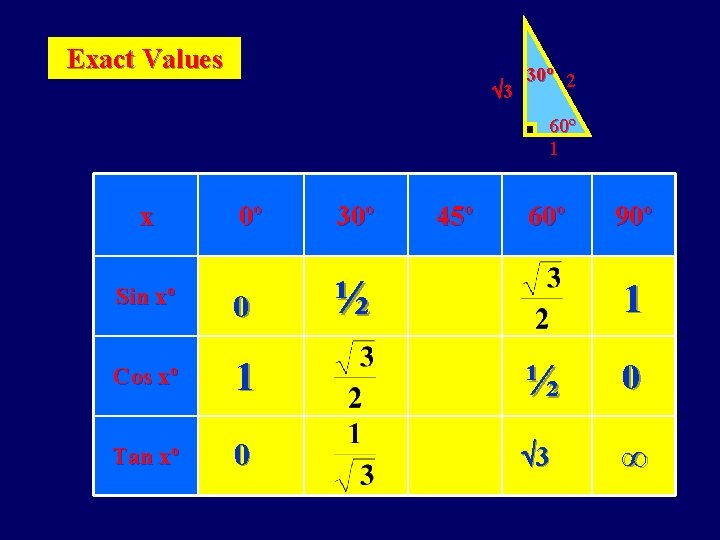
Exact Values 3 30º 2 60º 1 x 0º 30º 45º 60º 90º Sin xº 0 ½ Cos xº 1 ½ 0 Tan xº 0 3 ∞ 1

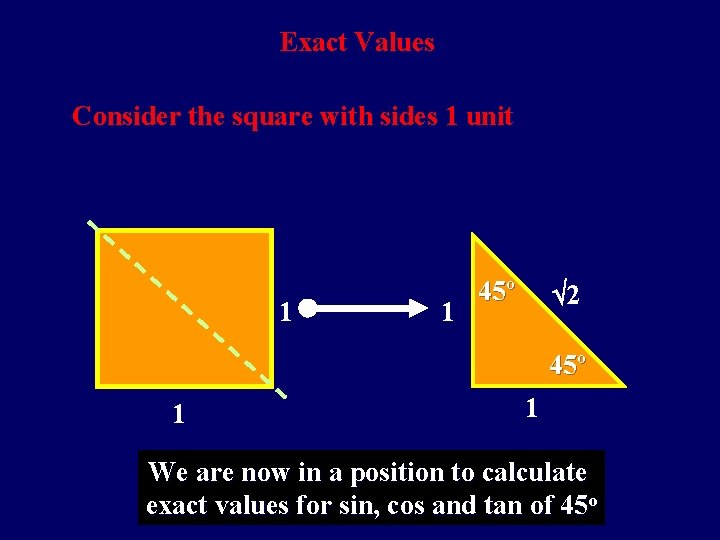
Exact Values Consider the square with sides 1 unit 1 1 45º 2 45º 1 1 We are now in a position to calculate exact values for sin, cos and tan of 45 o

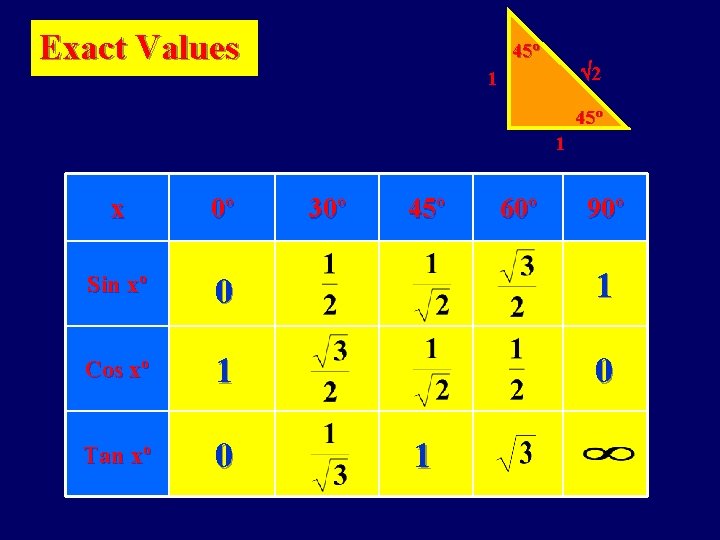
Exact Values 45º 2 1 45º 1 x 0º 30º 45º Sin xº 0 1 Cos xº 1 0 Tan xº 0 1 60º 90º

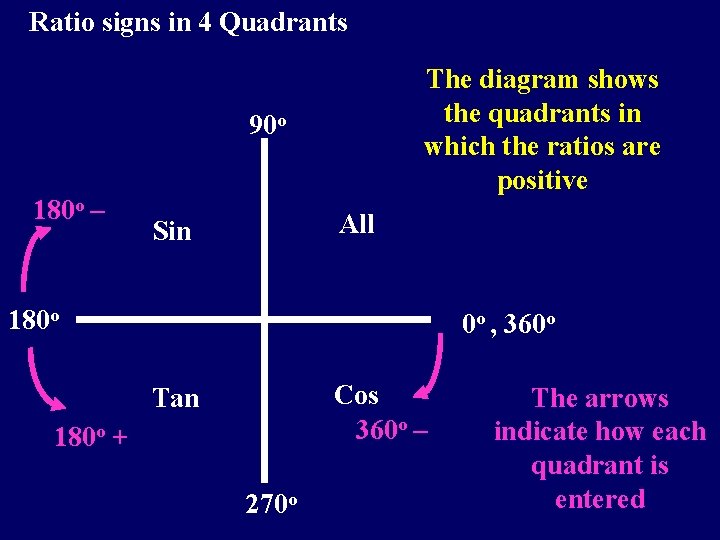
Ratio signs in 4 Quadrants The diagram shows the quadrants in which the ratios are positive 90 o 180 o – All Sin 180 o 0 o , 360 o Cos 360 o – Tan 180 o + 270 o The arrows indicate how each quadrant is entered

Exact value table and quadrant rules. tan 150 o = tan(180 - 30) = – o o tan 30 (Q 2 so neg) o cos 300 = cos(360 - 60) o = o cos 60 (Q so 4 = – 1/ √ 3 = 1/2 pos) o sin 120 = sin(180 - 60) o = sin 60 o = √ 3/ 2 (Q 2 so pos) o tan 300 = tan(360 - = – tan 60 o = – √ 3 o 60) (Q 4 so

Exact value table and quadrant rules. Find the exact value of cos 2 (5π/6) – sin 2 (π/6) cos (5π/6) cos 150 o= cos(180 - 30)=o – cos 30 o = – √ 3 /2 = (Q 2 so neg) sin (π/6) = sin 30 o = 1/2 cos 2 (5π/6) – sin 2 (π/6) = 1(- √ 3 /2)2 – = /2(1/ )2 2 = 3/ 4 1/ 4

Exact value table and quadrant rules. sin(2π/3) = sin 120 o = sin(180 – 60)o= sin= √ 3/2 60 o cos(2 π /3) = cos 120 o = cos(180 – 60)=o – cos = – 1/2 60 o tan(2 π /3) = tan 120 o = tan(180 – 60)=o –tan = - √ 3 60 o

Trig Identities An identity is a statement which is true for all values. (1) sin 2θ + cos 2 θ = 1θ ≠ an odd multiple of π/2 or 90° (2)tansin = θθ since this coswould θ mean dividing by 0

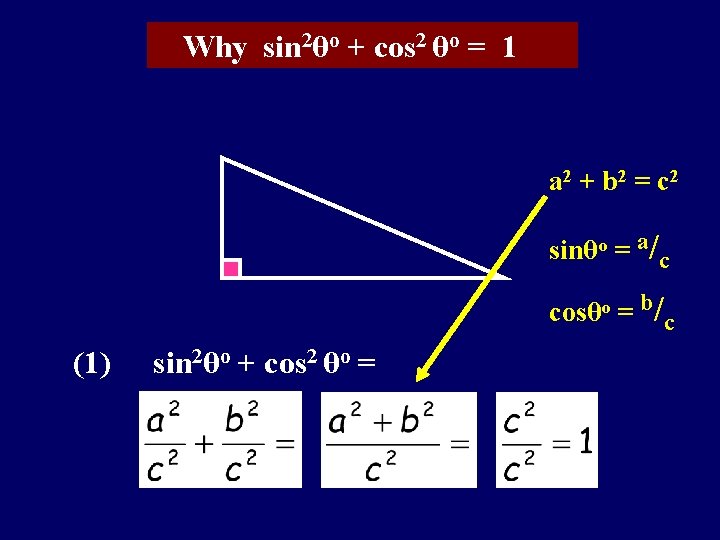
Why sin 2θo + cos 2 θo = 1 a 2 + b 2 = c 2 sinθo = a/c cosθo = b/c (1) sin 2θo + cos 2 θo =

Often you will have to rearrange the identities. sin 2θ + cos 2 θ = 1 Is the same as: sin 2 θ = 1 – cos 2 θ Is the same as: cos 2 θ = 1 – sin 2 θ

Using Trig Identities Example 1 Given sin θ = 5/13 where 0 < π/ θ < Find the exact 2 values of cos θ and tan θ. cos 2 θ = 1 - sin 2 θ Since θ is between 0 < θ < π/2 = 1 – (5/13)2 = 1– = 144/ 25/ 169 sinθ tan cos θ =θ = 169 cos θ = √(144/169) = 12/ 13 or 5/ 13 ÷ 12/13 5= = tan /13θ 5×/=12135//12 12 -12/ 13 cos θ = 12/13

Given that cos θ = -2/ √ 5 Find sin θ and tan θ. Since θ is between π < θ < 3π / 2 sin 2 θ = 1 - cos 2 θ = 1 – (-2/ √ 5 )2 Hence tan θ = 1/2 - 1/ -2 sinθ tan cos θ =and θ =sinθ =√ 5 - ÷ 1/ / √ 5 = 1 – 4/5 = 1/ √ 5 5 = sin θ = √(1/5) = 1/ √ 5 or where π < θ < 3π /2 - 1/ √ 5 × - √ 5 /2

Solving Trig Equations Solve sin 3 x = ½, for 0 < x < π sin-1 ½= /6 30 o, π S 180 – T A 0 < x < π (180 o) 0 < 3 x < 3π (540 o) C o, iexadd 360 o, 510 o to 540 Angles up angle NOT 3 x = 30 o, 150 o , Original 390 3 x = π/6, 5π/6, 13π/6, 17π/6 x = π/18, 5π/18, 13π/18, 17π/18 Now change to radians, multiples of original angle, 30 o = π/ 6

The following questions are on Graphs & Functons Non-calculator questions will be indicated

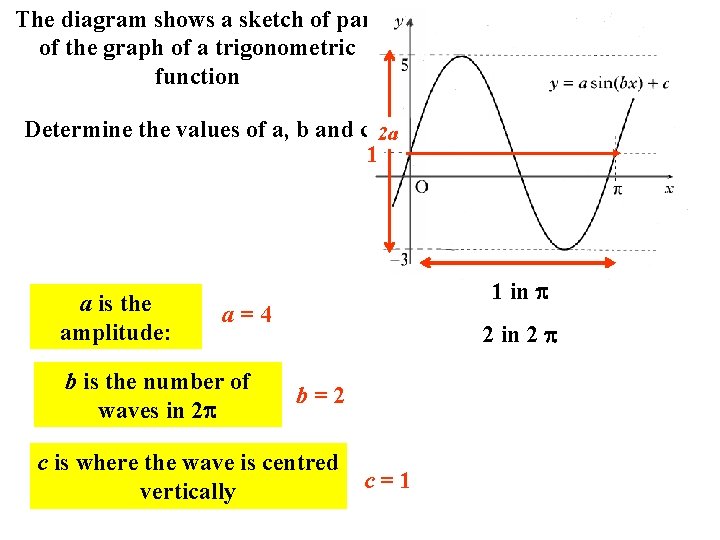
The diagram shows a sketch of part of the graph of a trigonometric function Determine the values of a, b and c 2 a 1 a is the amplitude: 1 in a=4 b is the number of waves in 2 2 in 2 b=2 c is where the wave is centred vertically c=1

Functions f and g are defined on suitable domains by f(x)= sin x and g(x) = 2 x. a) Find expressions for: i) f(g(x)) b) ii) g(f(x)) Solve 2 f(g(x)) = g(f(x)) for 0 ≤ x ≤ 360 a) b)

Functions are defined on a suitable set of real numbers. a) Find expressions for b) i) Show that ii) Find a similar expression for and hence solve the equation a) Now use exact values b) equation reduces to