Radians Degrees and Arc Length Skill 25 Objectives

Radians, Degrees, and Arc Length Skill 25

Objectives… • Describe angles • Use radian measure • Use degree measure and convert between degree and radian measure • Use angles to model and solve real-life problems
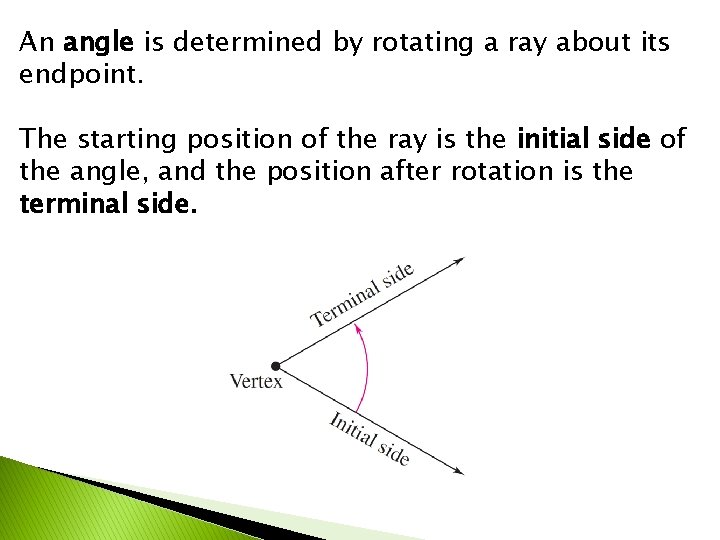
An angle is determined by rotating a ray about its endpoint. The starting position of the ray is the initial side of the angle, and the position after rotation is the terminal side.
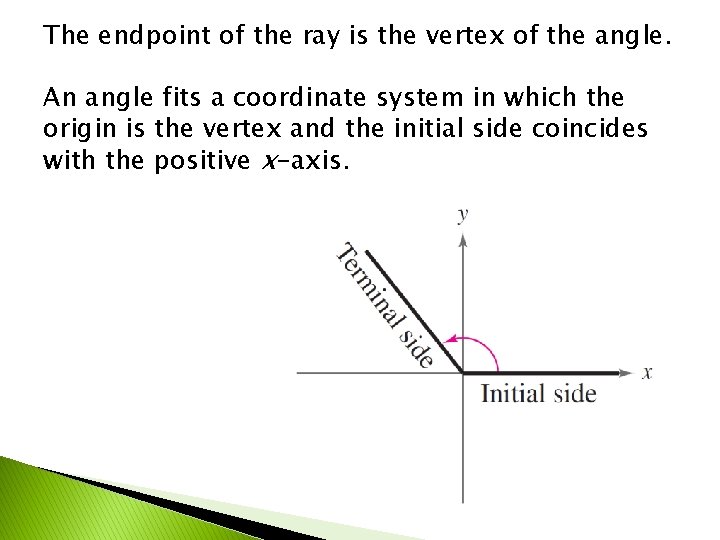
The endpoint of the ray is the vertex of the angle. An angle fits a coordinate system in which the origin is the vertex and the initial side coincides with the positive x-axis.

Positive angles are generated by counterclockwise rotation and negative angles by clockwise rotation.
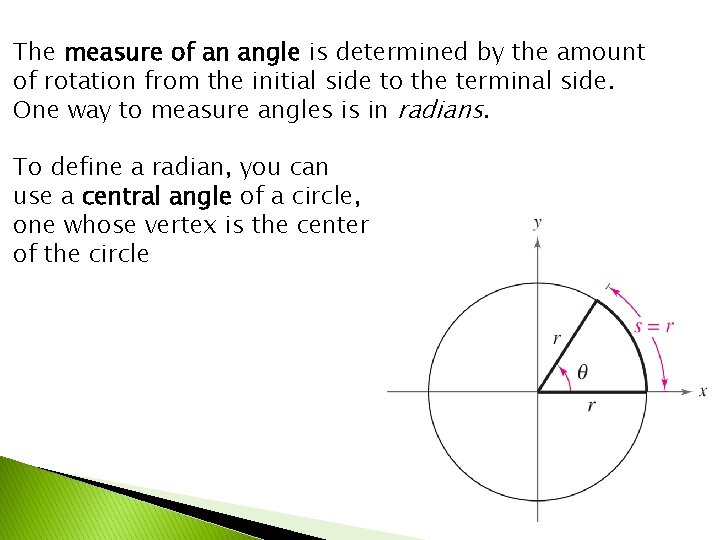
The measure of an angle is determined by the amount of rotation from the initial side to the terminal side. One way to measure angles is in radians. To define a radian, you can use a central angle of a circle, one whose vertex is the center of the circle

Because the circumference of a circle is 2 n units, it follows that a central angle of one full revolution (counterclockwise) corresponds to an arc length of s = 2 n.

The four quadrants in a coordinate system are numbered I, III, and IV.

A given angle θ has infinitely many coterminal angles. To find coterminal angles Add 2 nπ (negative) or subtract 2 nπ (positive) Is coterminal with
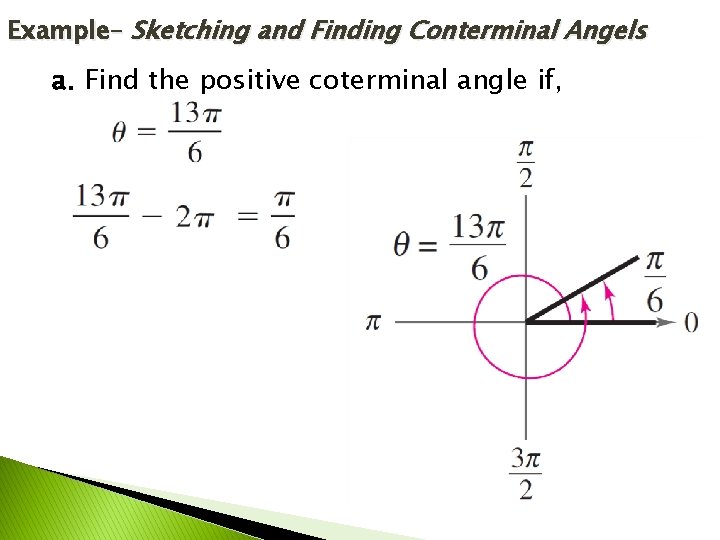
Example– Sketching and Finding Conterminal Angels a. Find the positive coterminal angle if,
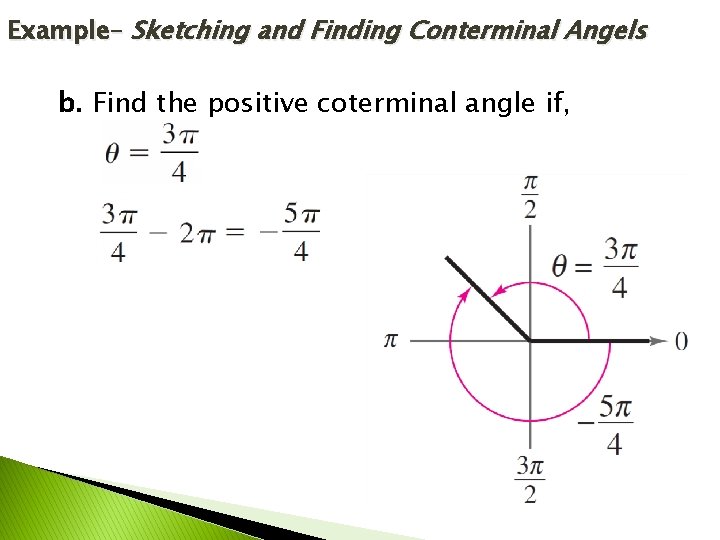
Example– Sketching and Finding Conterminal Angels b. Find the positive coterminal angle if,
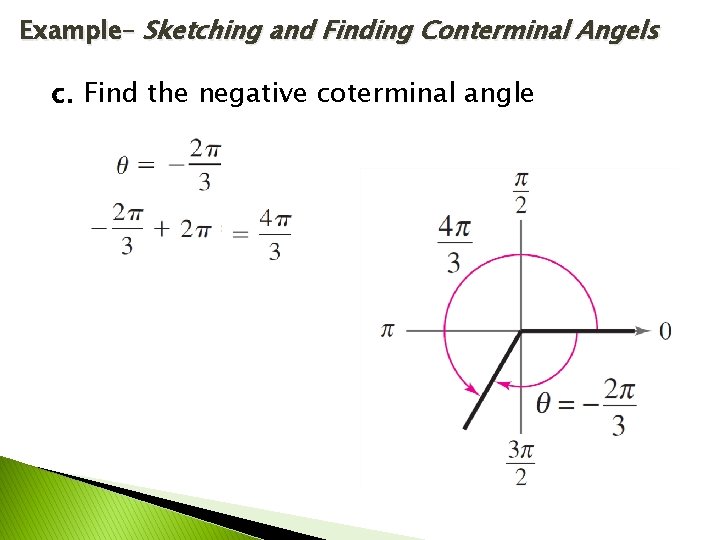
Example– Sketching and Finding Conterminal Angels c. Find the negative coterminal angle

A second way to measure angles is in terms of degrees.

Degree Measure Because 2 radians corresponds to one complete revolution, degrees and radians are related by the equations 360 = 2 rad and 180 = rad.


Degree Measure

Example– Converting From Degrees to Radians

Example– Converting From Radians to Degrees

It is common to write a degree measurement in a number of degrees, degrees minutes, minutes and seconds Symbols for degrees (°), minutes (‘), and seconds (")

Here's How: 1. The whole units of degrees will remain the same 2. Multiply the decimal by 60 = minutes 3. Take the remaining decimal and multiply by 60 = seconds 4. Take your three sets of numbers and put them together,

Example; convert the degrees to DºM’S” 315. 45º -134. 68º

Example; convert DºM’S” to decimal degrees 233º 14’ 23” -89º 52’ 10”
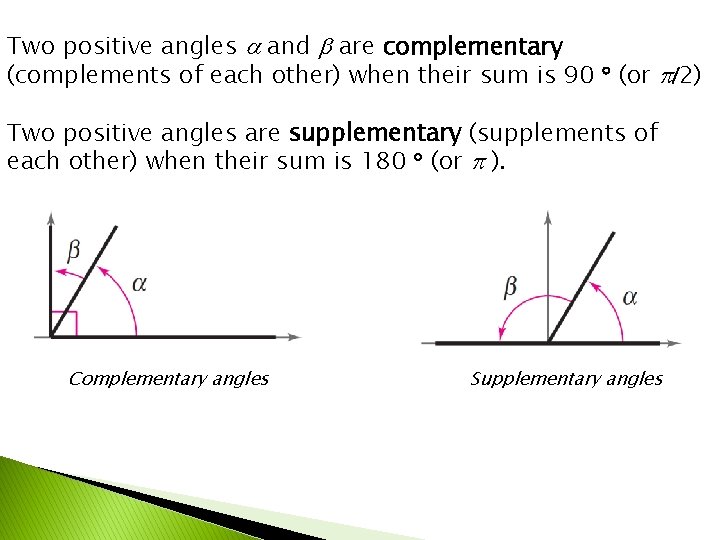
Two positive angles and are complementary (complements of each other) when their sum is 90 (or 2) Two positive angles are supplementary (supplements of each other) when their sum is 180 (or ). Complementary angles Supplementary angles

Example– Complementary and Supplementary Angels If possible, possible find the complement and supplement of each angle. a. 72 b. 148 c. d. Solution: a. The complement is 90 – 72 =18 The supplement is 180 – 72 = 108

Example– Solution b. Because 148 is greater than 90 it has no complement. (complements are positive angles. ) The supplement is 180 – 148 = 32 . c. The complement is The supplement is

Example– Solution d. Because 4 5 is greater than 2 it has no complement. The supplement is

For a circle radius r, a central angle θ then the arc length is
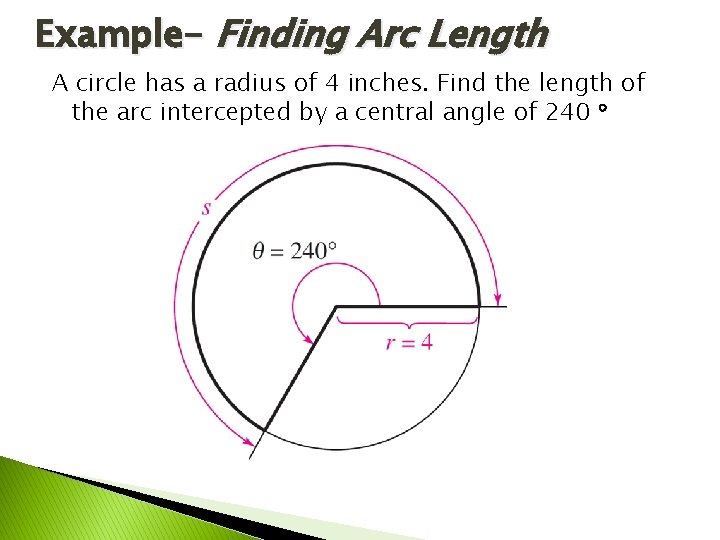
Example- Finding Arc Length A circle has a radius of 4 inches. Find the length of the arc intercepted by a central angle of 240

Example– Solution To use the formula s = r Convert 240 to radian measure. Then, using a radius of r = 4 inches, you can find the arc length to be

Example- Finding Arc Length A circle has a radius of 7 inches. Find the length of the arc intercepted by a central angle of 120

25: Radians, Degrees, and Arc Length � Summarize � Video � Homework ◦ Worksheet � Quiz Notes

Linear and Angular Speed

Example– Finding Linear Speed The second hand of a clock is 10. 2 centimeters long, as shown in Figure 4. 16. Find the linear speed of the tip of this second hand.

Example– Solution In one revolution, the arc length traveled is s = 2 r = 2 (10. 2) Substitute for r. = 20. 4 centimeters. The time required for the second hand to travel this distance is t =1 minute = 60 seconds.

Example– Solution So, the linear speed of the tip of the second hand is Linear speed = 1. 07 centimeters per second.
- Slides: 35