Radians and Angles Welcome to Trigonometry Starring Angles














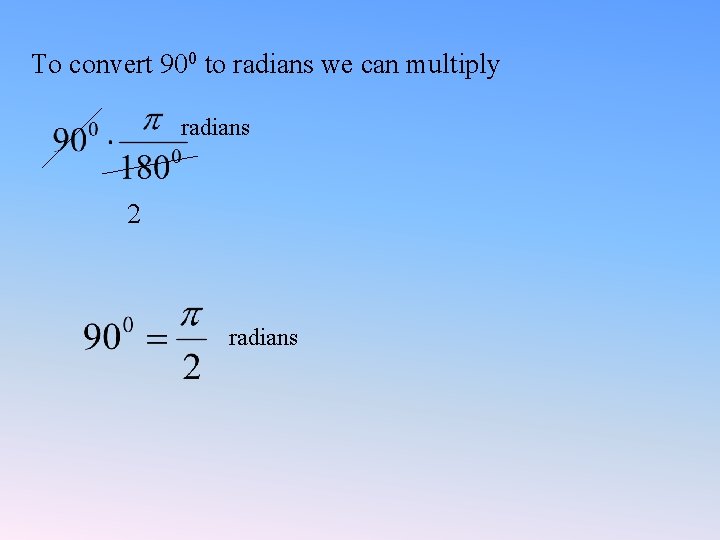
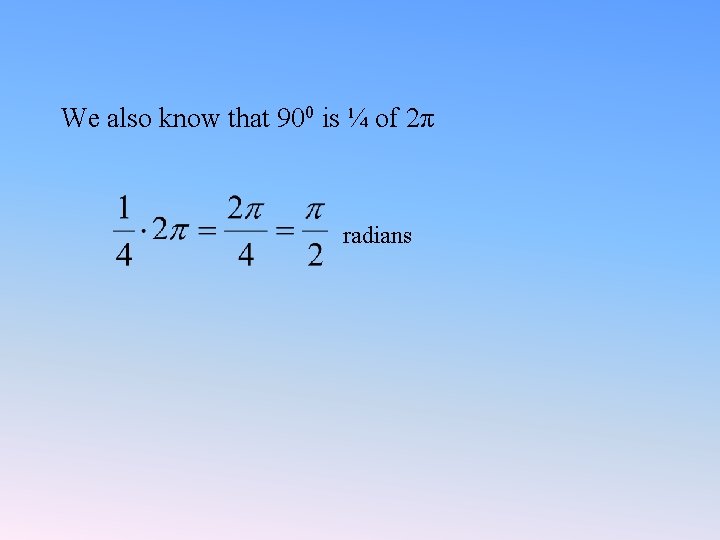













- Slides: 33

Radians and Angles Welcome to Trigonometry!! Starring Angles The Coterminal Angles Radian Sine Download Angles and Angle Degree. Measure HW Cosine Tangent Cosecant Cotangent Secant

Degree Measure Over 2500 years ago, the Babylonians used a number system based on 60 The number system we use today is based on 10 However we still use the Babylonian idea to measure certain things such as time and angles. That is why there are 60 minutes in an hour and 60 seconds in a minute.

The Babylonians divided a circle into 360 equally spaced units which we call degrees. In the DMS (degree minute second) system of angular measure, each degree is subdivided into 60 minutes (denoted by ‘ ) and each minute is subdivided into 60 seconds (denoted by “)

Since there are 60 ‘ in 1 degree we can convert degrees to minutes by multiplying by the conversion ratio

Convert 34. 80 to DMS We need to convert the fractional part to minutes

Convert 112. 420 to DMS Convert the fractional part of the minutes into seconds

Convert 42024’ 36’’ to degrees This is the reverse of the last example. Instead if multiplying by 60, we need to divide by 60

Radian Measure The circumference of a circle is 2πr In a unit circle, r is 1, therefore the circumference is 2π A radian is an angle measure given in terms of π. In trigonometry angles are measured exclusively in radians! 1

Radian Measure Since the circumference of a circle is 2π radians, 2π radians is equivalent to 360 degrees 1

Radian Measure Half of a revolution (1800) is equivalent to radians 1

Radian Measure One fourth of a revolution (900) is equivalent to radians 1

Since there are 2π radians per 3600, we can come up with the conversion ratio of radians degrees Which reduces to radians degrees

To convert degrees to radians multiply by radians degrees

To convert radians to degrees multiply by degrees radians
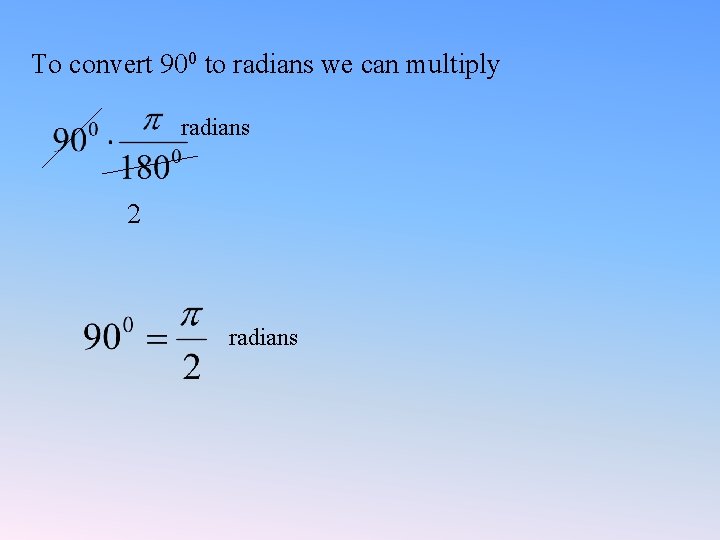
To convert 900 to radians we can multiply radians 2 radians
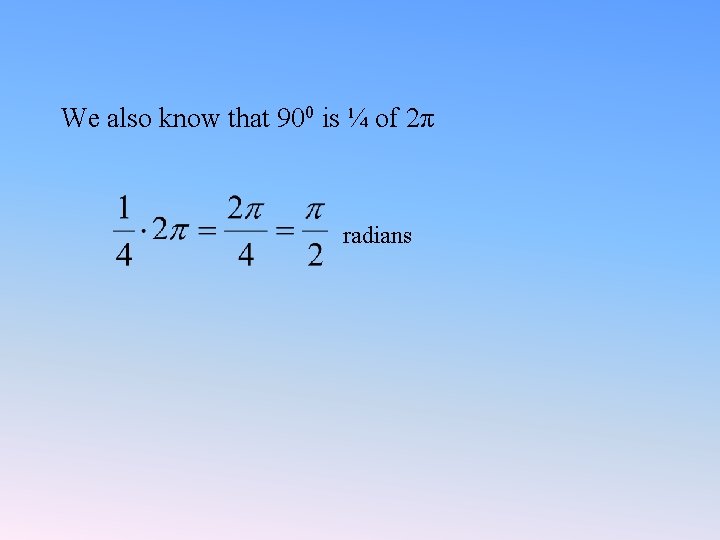
We also know that 900 is ¼ of 2π radians

Arc length formula If θ (theta) is a central angle in a circle of radius r, and if θ is measured in radians, then the length s of the intercepted arc is given by r s θ THIS FORMULA ONLY WORKS WHEN THE ANGLE MEASURE IN IS RADIANS!!!

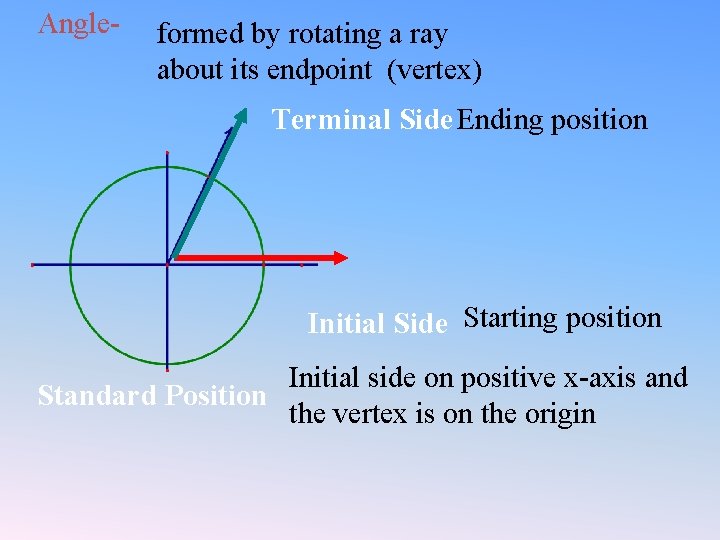
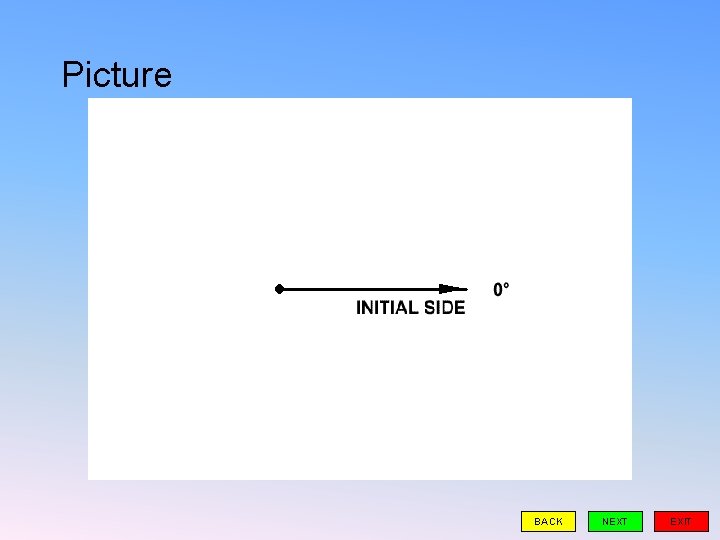
Angle- formed by rotating a ray about its endpoint (vertex) Terminal Side Ending position Initial Side Starting position Initial side on positive x-axis and Standard Position the vertex is on the origin

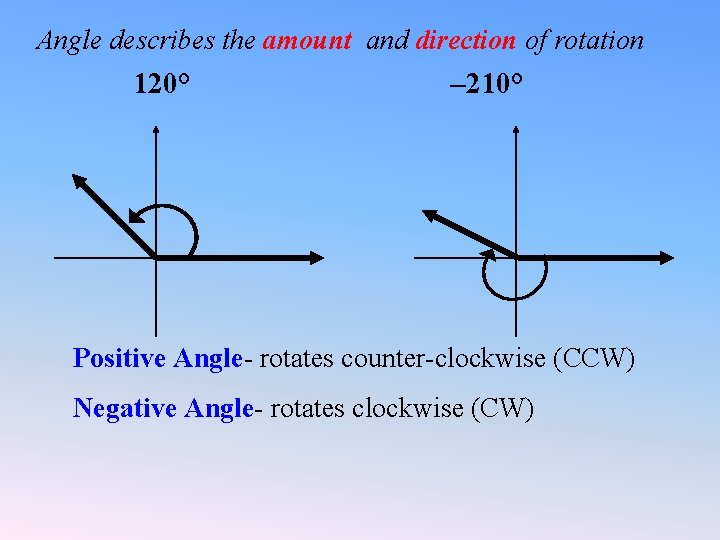
Angle describes the amount and direction of rotation 120° – 210° Positive Angle- rotates counter-clockwise (CCW) Negative Angle- rotates clockwise (CW)

Coterminal Angles • Angles with the same initial side and same terminal side, but have different rotations, are called coterminal angles. • 50° and 410° are coterminal angles. Their measures differ by a multiple of 360.

Q: Can we ever rotate the initial side counterclockwise more than one revolution? Answer – YES! BACK NEXT EXIT

Note: Complete Revolutions Rotating the initial side counterclockwise 1 rev. , 2 revs. , 3 revs. , . . . generates the angles which measure 360 , 720 , 1080 , . . . BACK NEXT EXIT

Picture BACK NEXT EXIT

ANGLES 360, 720, & 1080 ARE ALL COTERMINAL ANGLES!

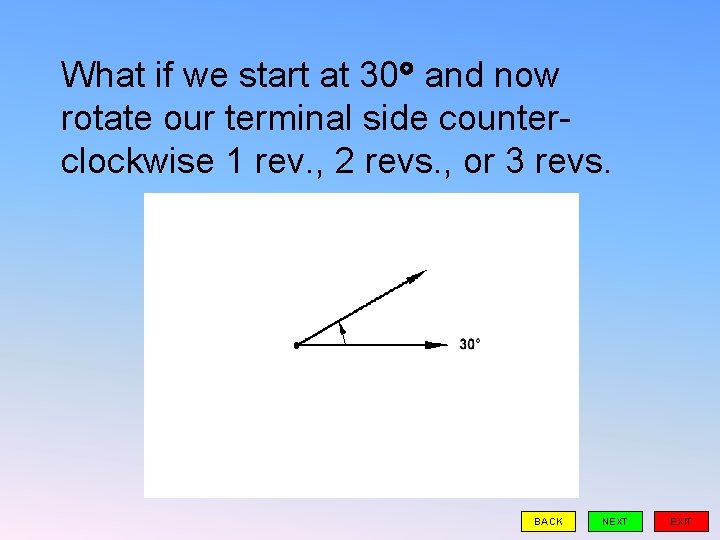
What if we start at 30 and now rotate our terminal side counterclockwise 1 rev. , 2 revs. , or 3 revs. BACK NEXT EXIT

Coterminal Angles: Two angles with the same initial and terminal sides Find a positive coterminal angle to 20º Find a negative coterminal angle to 20º Find 2 coterminal angles to

Warm Up • Convert to Degrees minutes, seconds • Convert to Radians:

Now, you try… Find two coterminal angles (+ & -) to What did you find? These are just two possible answers. Remember…there are more!

Complementary Angles: Two angles whose sum is 90 Supplementary Angles: Two angles whose sum is 180

To convert from degrees radians, multiply by To convert from radians degrees, multiply by Convert to radians:

To convert from degrees radians, multiply by To convert from radians degrees, multiply by Convert to degrees: So, you think you got it now?

Express 50. 525 in degrees, minutes, seconds 50º +. 525(60) 50º + 31. 5 50º + 31 +. 5(60) 50 degrees, 31 minutes, 30 seconds

CW/HW • Page 280 -281 (1, 3, 5 -8, 11 -14, 3033)