Radial Basis Functions Pedro Teodoro What For Radial

Radial Basis Functions Pedro Teodoro

What For Radial Basis Functions (RBFs) allows for interpolate/approximate scattered data in n. D. 2

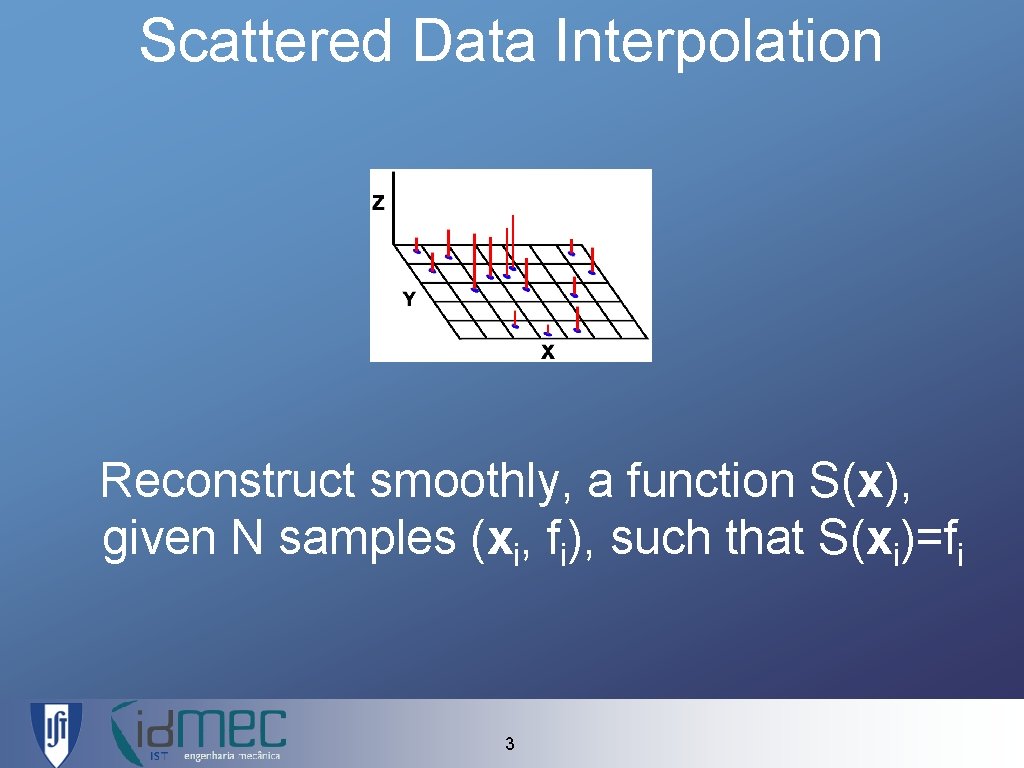
Scattered Data Interpolation Reconstruct smoothly, a function S(x), given N samples (xi, fi), such that S(xi)=fi 3

Radial Basis Function method 4

Global Support Basis Functions These basis functions guarrantes solution for the entire domain 5

Finding the RBF coefficients Results by solving the following linear System Solution Slow Storage 6

Closed Curves and Surfaces In case of having point clouds defining a curve or a surface, we want to obtain a distance field, where its isovalues defines the surface, otherwise, the solution would be a constant in all the domain. For that, we define offsurface points and assign: • Positive values (outside) • Negative values (inside) 7

Closed Curves and Surfaces (cont) If for every point, we assign two more points (one inside and one outside), the interpolant is: Solution Slower Storage 8

Improvements Fast. RBF toolbox uses the Fast Multipole Method algorithm to solve the linear system. Solution Storage Feasible but matematically complex and proprietary 9

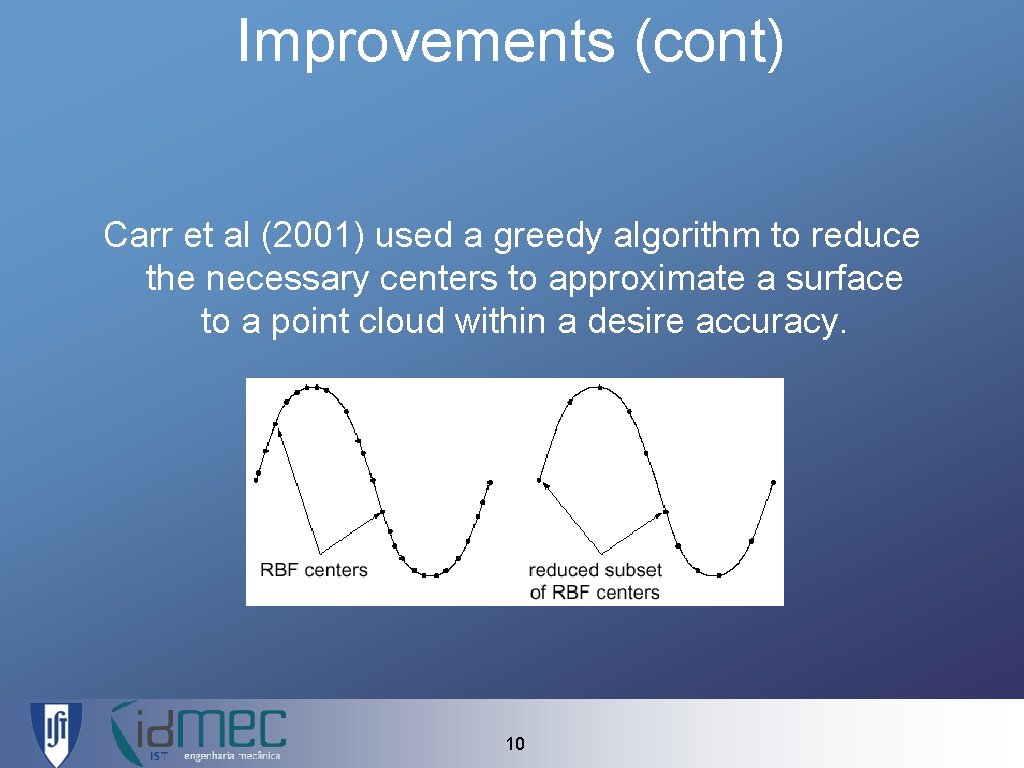
Improvements (cont) Carr et al (2001) used a greedy algorithm to reduce the necessary centers to approximate a surface to a point cloud within a desire accuracy. 10

Improvements (cont) Walder et al (2006) shown that it is possible to obtain na implicit surface without offsurface points, neither normals information. Solution Storage 11

Improvements (cont) Rong. Jiang et al (2009) assuming that the imput point cloud is oriented (normals information), simplified the work of Walder et al (2006). Solution Storage 12

Goal Implement the greedy algorithm of Carr et al (2001) and of Rong. Jiang et al (2009), to interpolate oriented point clouds… … along with a divide to conquer algorithm based on Partition of Unity (PU) with blending functions to reduce the computational power and storage. Solution Storage 13

Bibliography • Reconstruction and Representation of 3 D Objects with Radial Basis Functions J. C. Carr, R. K. Beatson, J. B. Cherrie T. J. Mitchell, W. R. Fright, B. C. Mc. Callum and T. R. Evans, ACM SIGGRAPH 2001, Los Angeles, CA, pp 67 -76, 12 -17 August 2001. • Implicit surface Modeling eith a Globally Regularised Basis of Compact Suport C. Walder, B. Scholkopf, O. Chappele, Eurographics 2006. • Hermite variational implicit surface reconstruction PAN Rong. Jiang, MENG Xiang. Xu, WHANGBO Taeg. Keun, Science in China Press, 2009. 14

Thanks 15