Quiz Week 6 Let s be a state

Quiz (Week 6) Let s be a state in a search space. 1. Draw a figure and explain f(s)=g(s)+h(s). 2. Explain the differences between f, g, h and f*, g*, h*.

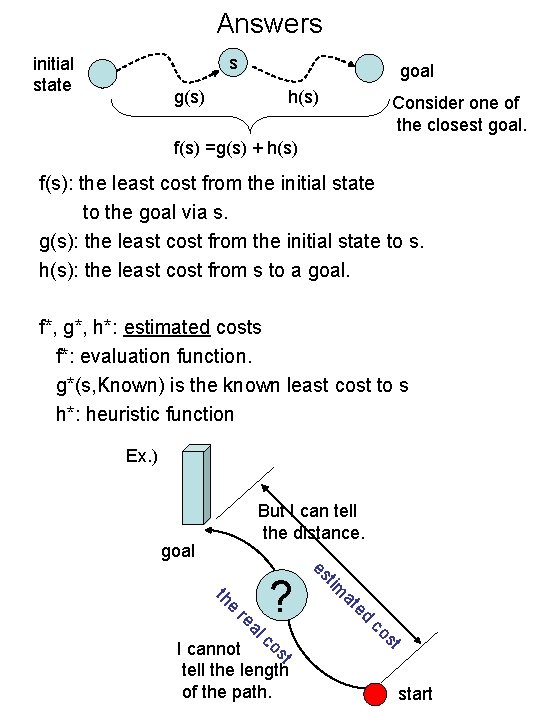
Answers s initial state goal g(s) h(s) Consider one of the closest goal. f(s) =g(s) + h(s) f(s): the least cost from the initial state to the goal via s. g(s): the least cost from the initial state to s. h(s): the least cost from s to a goal. f*, g*, h*: estimated costs f*: evaluation function. g*(s, Known) is the known least cost to s h*: heuristic function Ex. ) But I can tell the distance. goal ed at tim st co al re I cannot tell the length of the path. es e th ? start

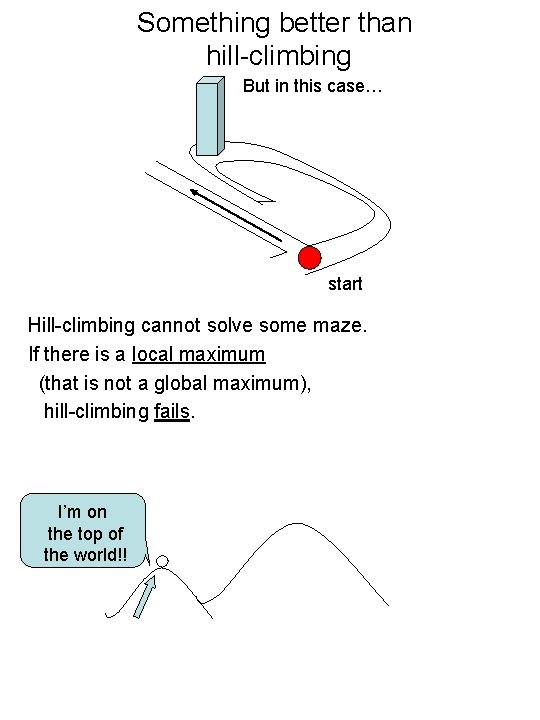
Something better than hill-climbing But in this case… start Hill-climbing cannot solve some maze. If there is a local maximum (that is not a global maximum), hill-climbing fails. I’m on the top of the world!!

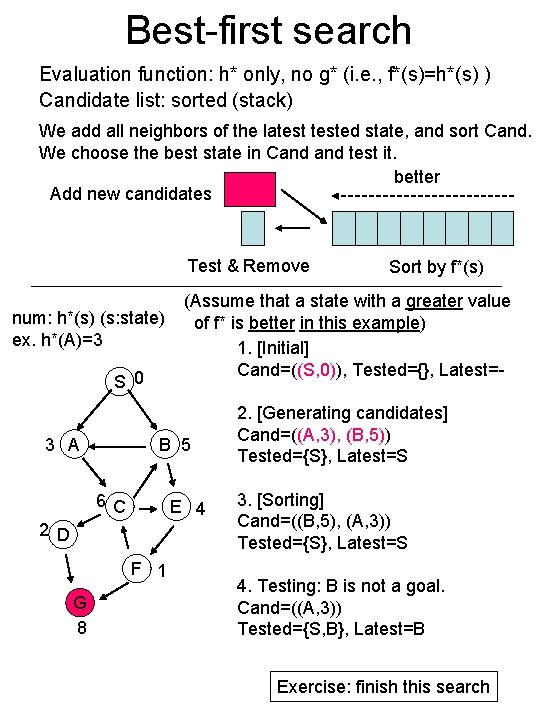
Best-first search Evaluation function: h* only, no g* (i. e. , f*(s)=h*(s) ) Candidate list: sorted (stack) We add all neighbors of the latested state, and sort Cand. We choose the best state in Cand test it. better Add new candidates Test & Remove num: h*(s) (s: state) ex. h*(A)=3 S 0 3 A E 4 2 D F 1 G 8 (Assume that a state with a greater value of f* is better in this example) 1. [Initial] Cand=((S, 0)), Tested={}, Latest=- B 5 6 C Sort by f*(s) 2. [Generating candidates] Cand=((A, 3), (B, 5)) Tested={S}, Latest=S 3. [Sorting] Cand=((B, 5), (A, 3)) Tested={S}, Latest=S 4. Testing: B is not a goal. Cand=((A, 3)) Tested={S, B}, Latest=B Exercise: finish this search

(note) If h* is a constant function, best-first search behaves in the same way as DFS. (Hint: stack) Best-first search does not guarantee that it finds the best path.

In-class exercise: Heuristic functions and best-first search Question. Create a maze, Apply best-first search and find the goal. Consider two cases. Let s be a state. a) h*(s): the distance between s and the goal b) h*(s): the Manhattan distance between s and the goal. (Manhattan distance between (x 1, y 1) and (x 2, y 2) is |x 1 -x 2|+|y 1 -y 2|)

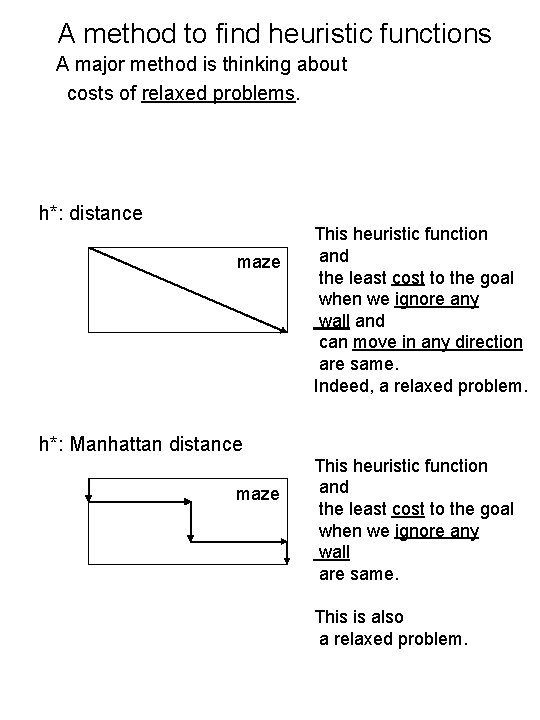
A method to find heuristic functions A major method is thinking about costs of relaxed problems. h*: distance maze This heuristic function and the least cost to the goal when we ignore any wall and can move in any direction are same. Indeed, a relaxed problem. h*: Manhattan distance maze This heuristic function and the least cost to the goal when we ignore any wall are same. This is also a relaxed problem.

訂正 Evaluation functions Here we consider a path from the initial state via state s to a goal. initial state s g(s) goal h(s) Consider one of the closest goal. f(s) =g(s) + h(s) Let f(s) be the least cost from the initial state to s and g(s) be that from s to a goal. ・Usually, we cannot tell the precise least cost to a goal. ・Then we estimate the cost to a goal. // f*(s) f* is called evaluation function. f*(s) is defined for each state in the state space. ・Let Known be a set of states. g*(s, Known) is the known least cost from the initial state to s. The value depends on set Tested and Cand. (We must update g* when we find a shorter path. ) Then g*(s, Known)≧g(s)