Quiz 1 Intro to Geometry Week 1 Day

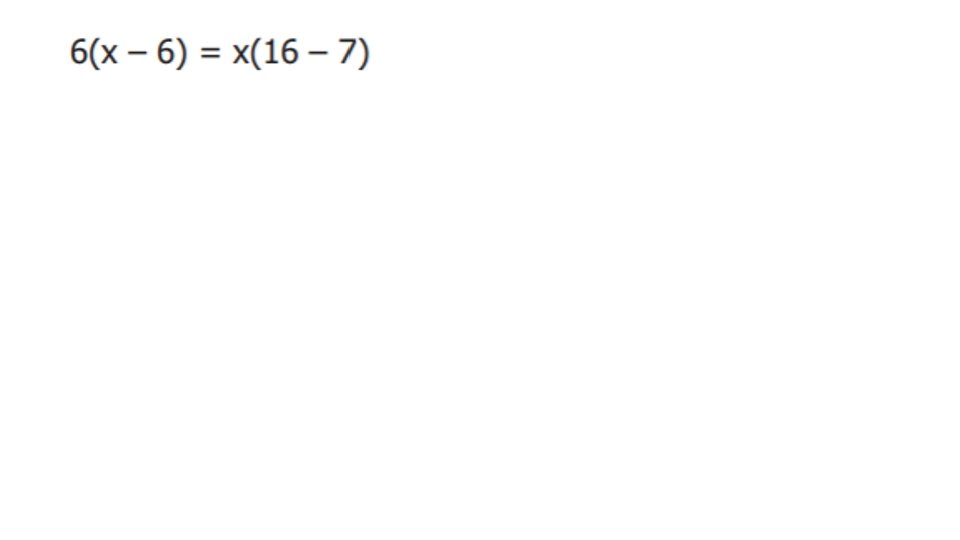

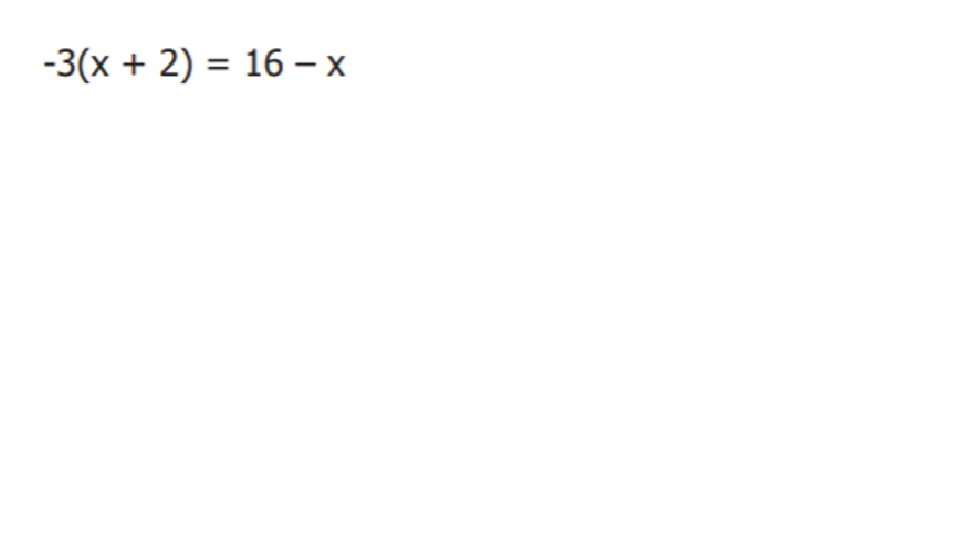
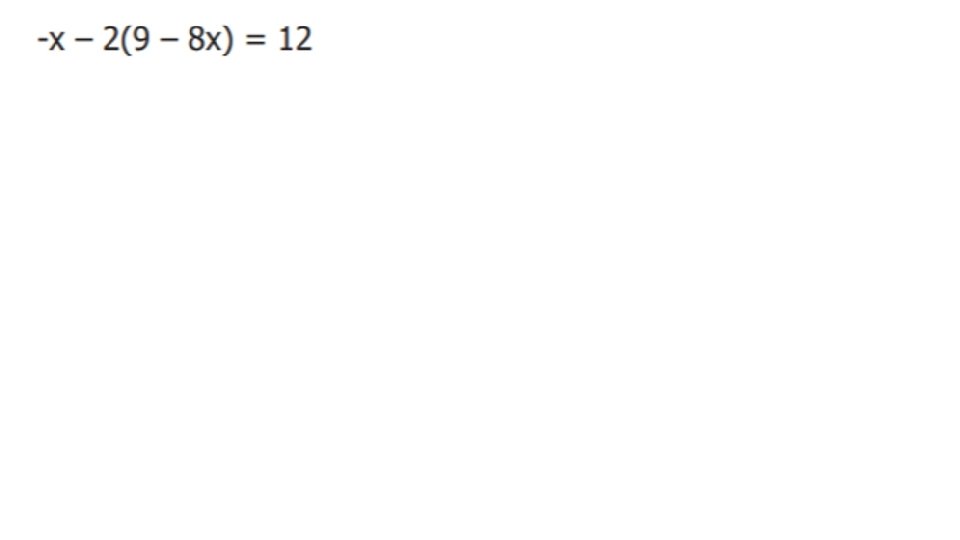







![Greek mathematician, often referred to as the "founder of geometry"[1] or the "father of Greek mathematician, often referred to as the "founder of geometry"[1] or the "father of](https://slidetodoc.com/presentation_image_h2/769057ead0cbe7ee97846b8f3e660832/image-21.jpg)












- Slides: 36

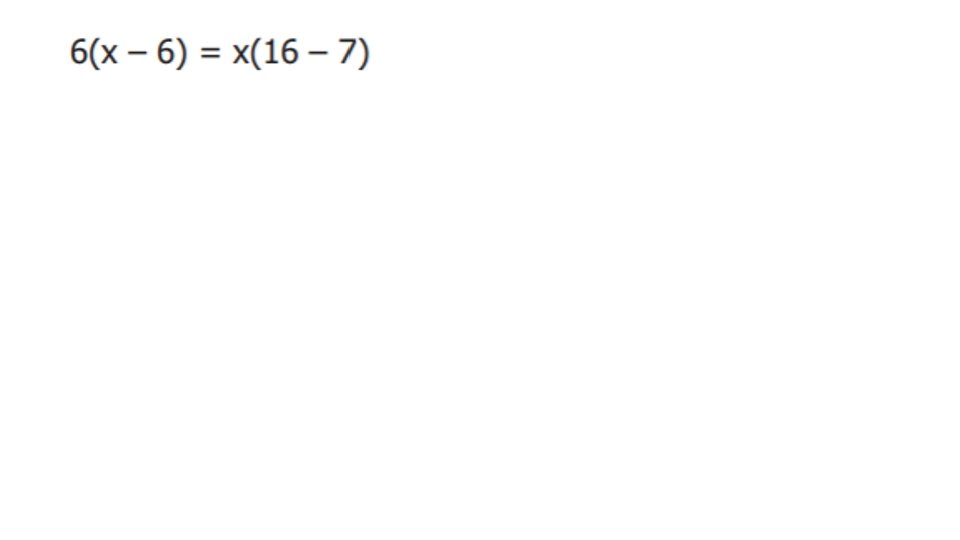

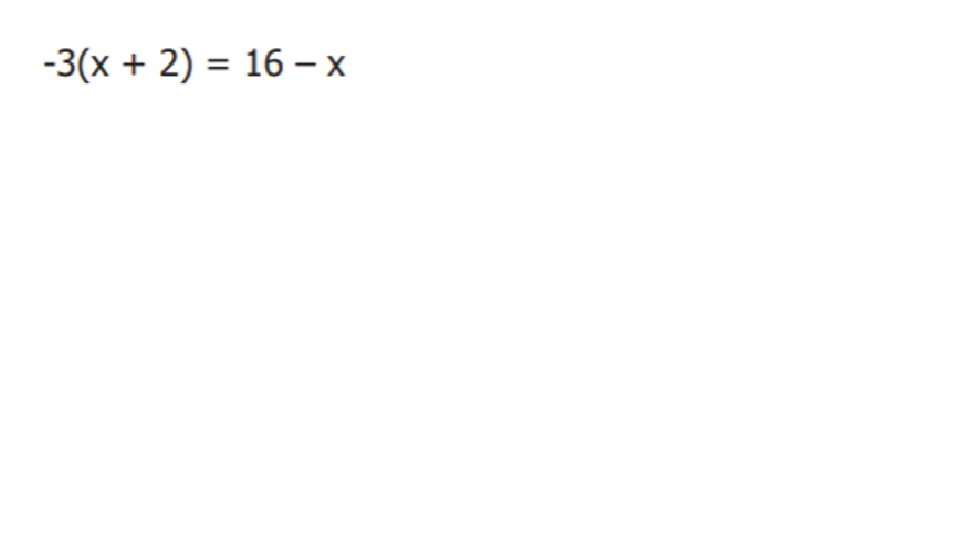
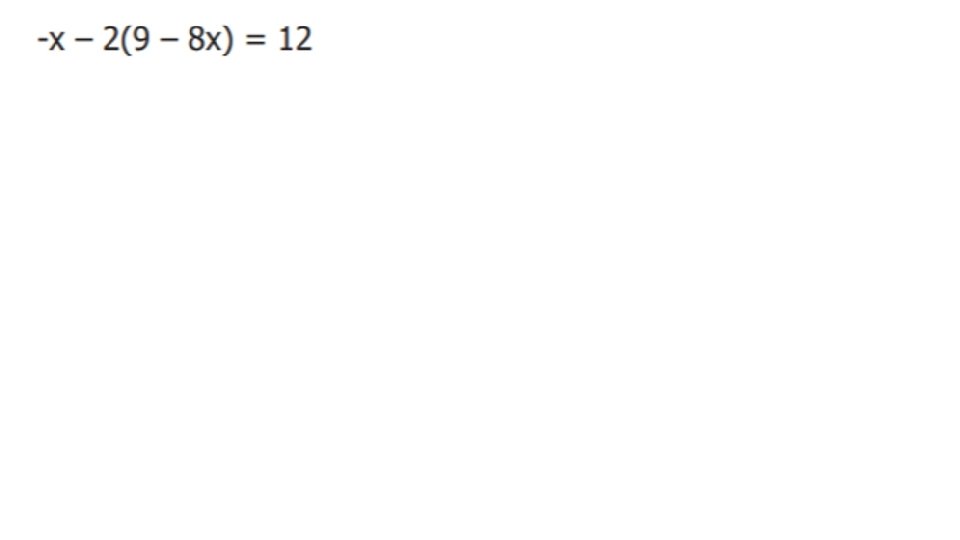

Quiz #1

Intro to Geometry Week 1 - Day 2 Basic Geometric Figures and Constructions Points, Lines, Segments and Circles

Objectives G-CO. A. 1 Know precise definitions based on the undefined notions of point, line, distance along a line, and distance around a circular arc. G. CO. D. 12 Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc. ).

Student Outcomes Students communicate mathematical ideas effectively and efficiently.

Student Outcomes The student will be able to use the four basic constructions to construct: • Congruent line segments • An equilateral triangle

Vocabulary

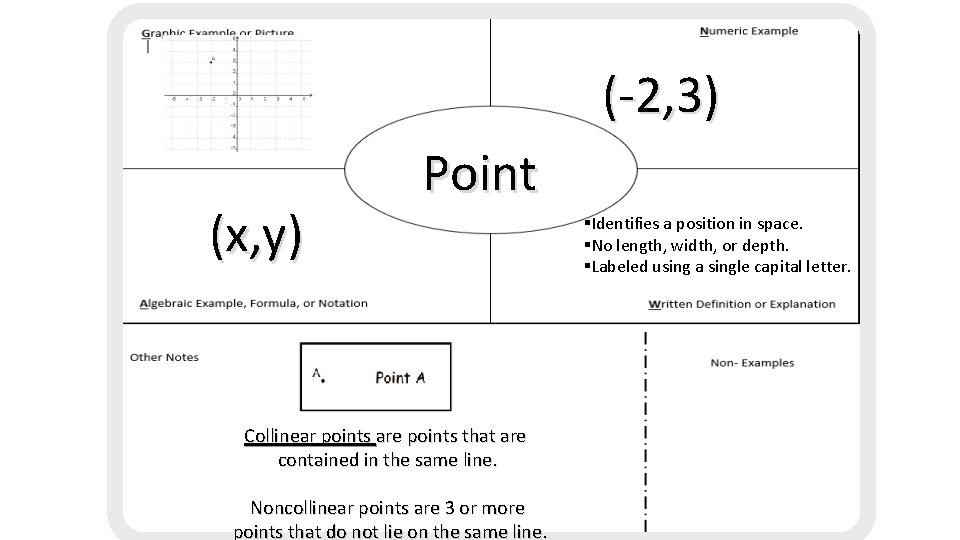
(-2, 3) (x, y) Point Collinear points are points that are contained in the same line. Noncollinear points are 3 or more points that do not lie on the same line. §Identifies a position in space. §No length, width, or depth. §Labeled using a single capital letter.

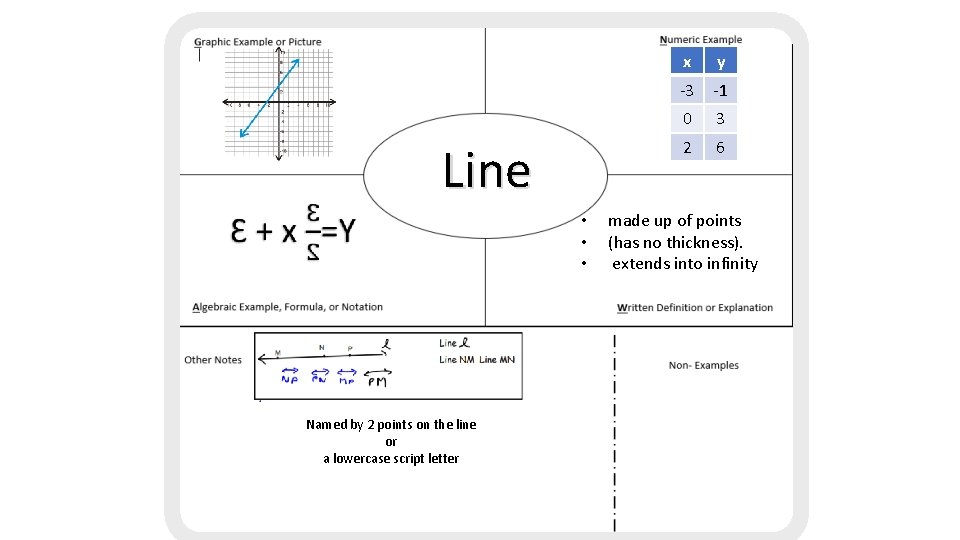
Line • • • Named by 2 points on the line or a lowercase script letter x y -3 -1 0 3 2 6 made up of points (has no thickness). extends into infinity

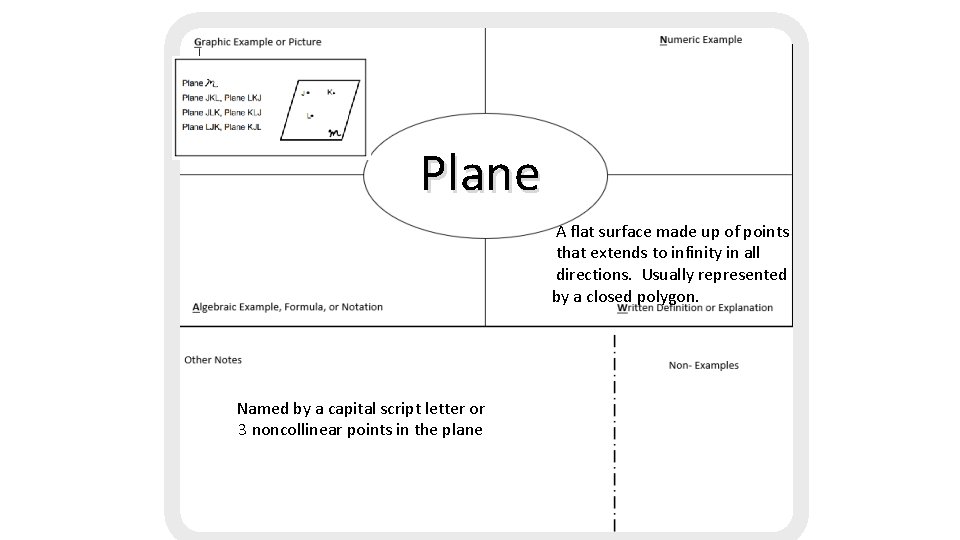
Plane A flat surface made up of points that extends to infinity in all directions. Usually represented by a closed polygon. Named by a capital script letter or 3 noncollinear points in the plane

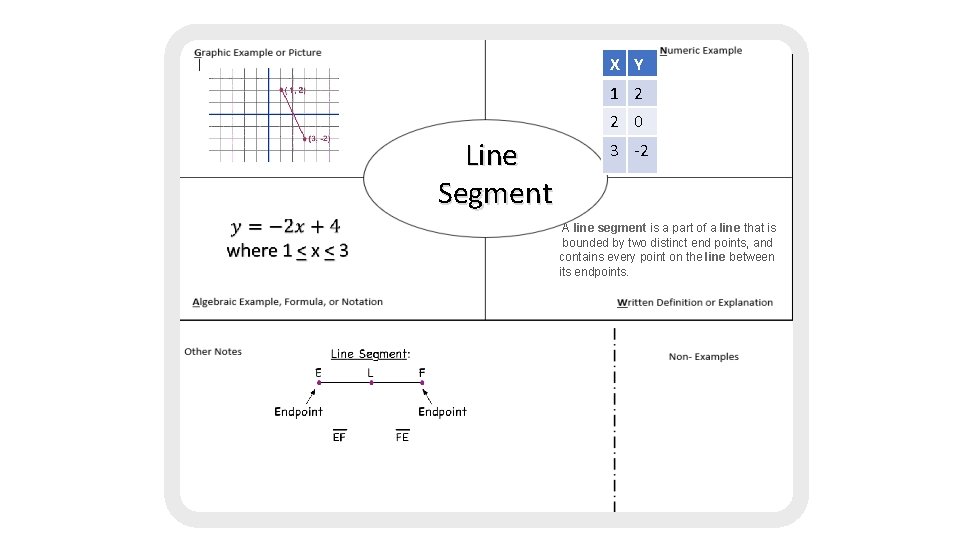
X Y 1 2 2 0 Line Segment 3 -2 A line segment is a part of a line that is bounded by two distinct end points, and contains every point on the line between its endpoints.

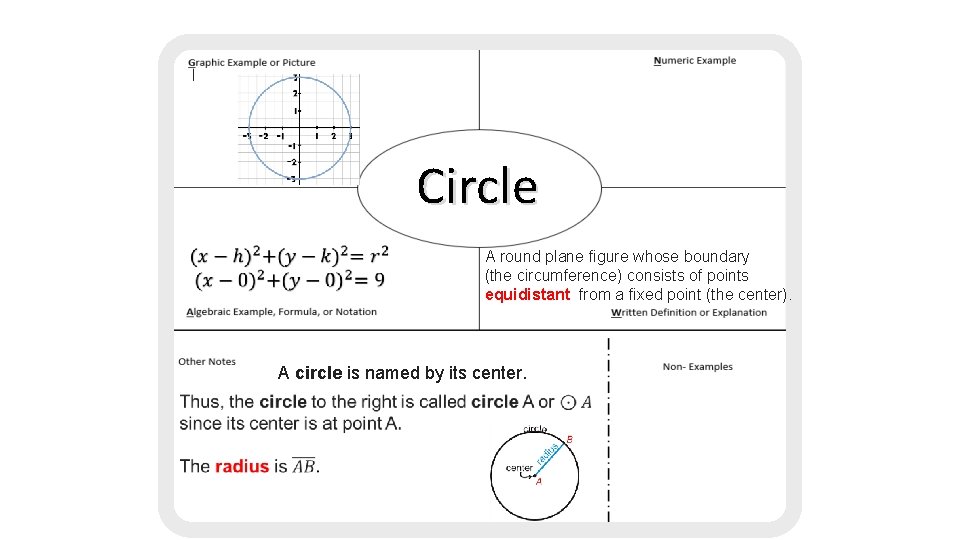
Circle A round plane figure whose boundary (the circumference) consists of points equidistant from a fixed point (the center). A circle is named by its center.

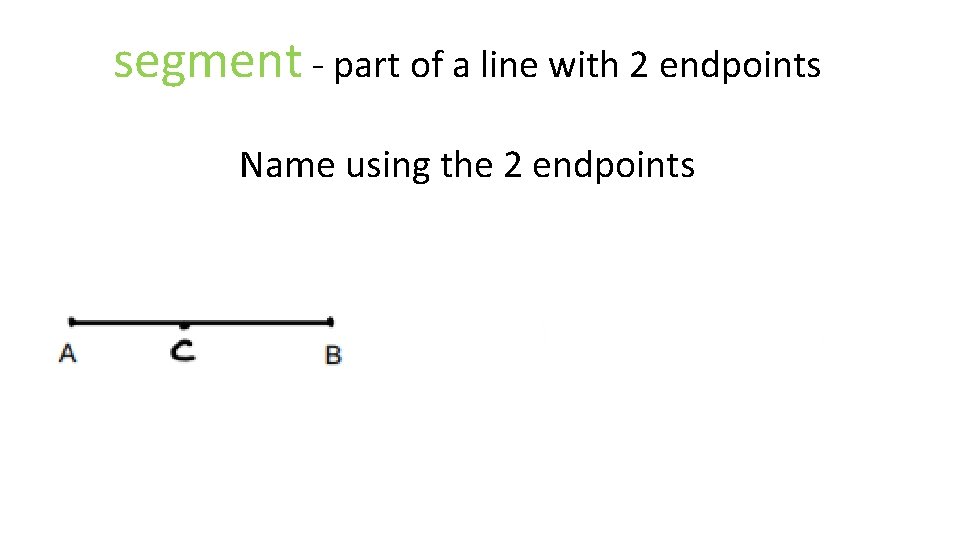
segment - part of a line with 2 endpoints Name using the 2 endpoints

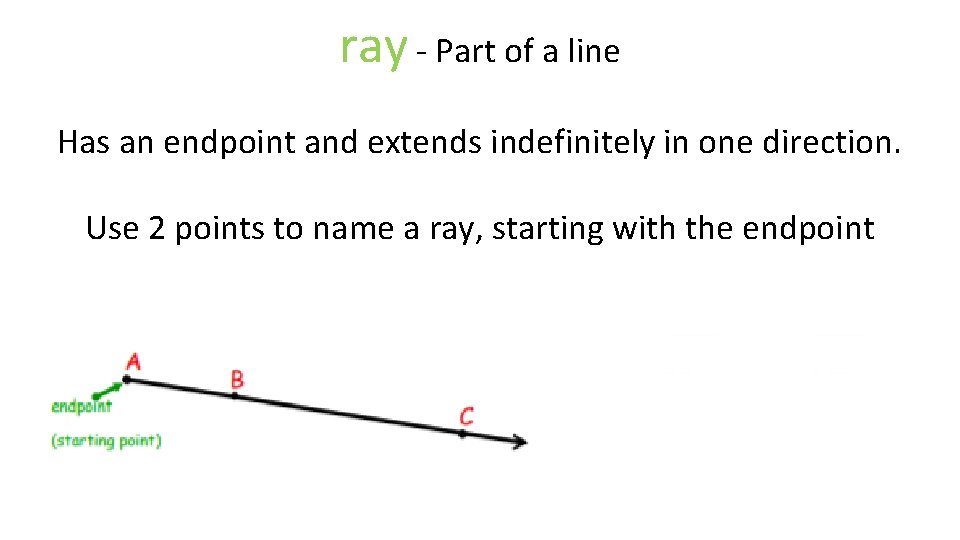
ray - Part of a line Has an endpoint and extends indefinitely in one direction. Use 2 points to name a ray, starting with the endpoint


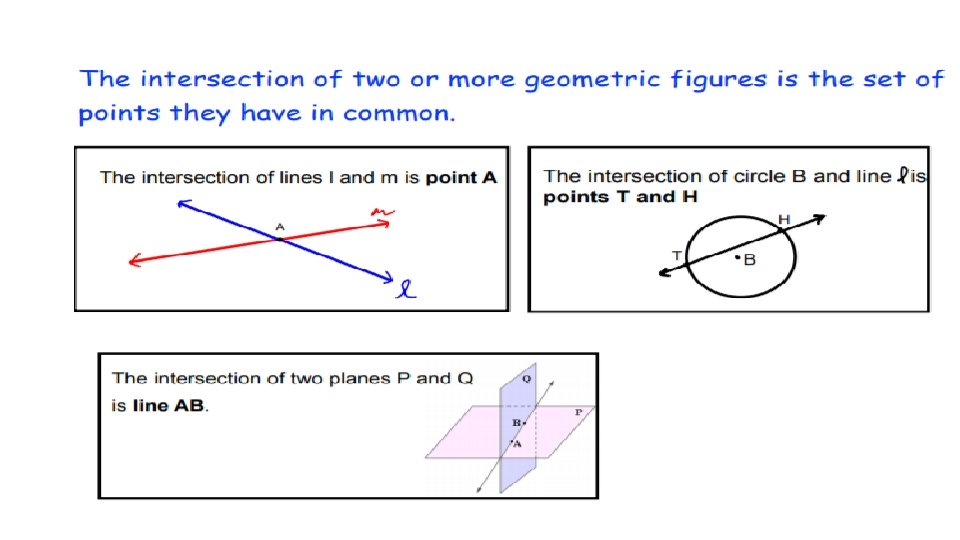
COPLANAR- two or more figures that lie in the same plane NONCOPLANAR – Two or more figures that are NOT in the same plane.
![Greek mathematician often referred to as the founder of geometry1 or the father of Greek mathematician, often referred to as the "founder of geometry"[1] or the "father of](https://slidetodoc.com/presentation_image_h2/769057ead0cbe7ee97846b8f3e660832/image-21.jpg)
Greek mathematician, often referred to as the "founder of geometry"[1] or the "father of geometry". He was active in Alexandria during the reign of Ptolemy I (323– 283 BC). His Elements is one of the most influential works in the history of mathematics, serving as the main textbook for teaching mathematics(especially geometr y) from the time of its publication until the late 19 th or early 20 th century.

It is a collection of definitions, postulates, propositions (theorems and constructions), and mathematical proofs of the propositions. The books cover plane and solid Euclidean geometry, elementary number theory, and incommensurable lines. Elements is the oldest extant large-scale deductive treatment of mathematics. It has proven instrumental in the development of logic and modern science, and its logical rigor was not surpassed until the 19 th century. Euclid's Elements has been referred to as the most successful[1][2] and influential[3] textbook ever written. It was one of the very earliest mathematical works to be printed after the invention of the printing press and has been estimated to be second only to the Bible in the number of editions published since the first printing in 1482,

Axioms and Postulates In Geometry, "Axiom" and "Postulate" are essentially interchangeable. In antiquity, they referred to propositions that were "obviously true" and only had to be stated, and not proven. The ancient Greeks recognized the difference between these two concepts. Axioms are self-evident assumptions, which are common to all branches of science, while postulates are related to the particular science. In modern mathematics there is no longer an assumption that axioms are "obviously true". Axioms are merely 'background' assumptions we make. The best analogy is that axioms are the "rules of the game". In Euclid's Geometry, the main axioms/postulates are:

Axioms/Postulates (accepted truths) 4 Basic Constructions 1. 2. 3. 4. Through any two points there is exactly one line. Any terminated line may be extended indefinitely. A circle may be drawn with any given point as center and any given radius. If two distinct lines intersect, they intersect at exactly one point.

Through any two points there is exactly one line.

Any terminated line may be extended indefinitely.

If two distinct lines intersect, they intersect at exactly one point.

A circle may be drawn with any given point as center and any given radius.







