Quit Divisors Friendly Numbers Sociable Numbers Quadratic Formula

Quit

Divisors Friendly Numbers Sociable Numbers Quadratic Formula Quit

Divisors • Divisors are all the numbers which divide evenly into a number including the number 1, but not including the number itself in the case of friendly and sociable numbers • Therefore the divisors of 24 are 1, 2, 3, 4, 6, 8 and 12 • They sum to 36 Quit

Friendly Numbers • These are pairs of numbers such that each number is the sum of the divisors of the other number. • Talismen sold in the middle ages would be inscribed with these numbers, on the grounds that they would promote love. • An Arab mathematician claims that people would write one of the pair of numbers on one fruit and eat it, writing the second number on another fruit and give it to a lover as a mathematical aphrodisiac! Quit

Friendly Numbers • There was only one pair discovered until Fermat discovered the pair 17, 296 and 18, 416 in 1636 • Descartes discovered the pair 9, 363, 584 and 9, 437, 056 in 1638 • In 1866 a sixteen year old Italian found the pair 1184 and 1210 • Computers can be programmed to find larger ones now! Quit

Project • The divisors of 1184 are 1, 2, 4, 8, 16, 32, 37, 74, 148, 296, 592 • Sum = 1210 • The divisors of 1210 are 1, 2, 5, 10, 11, 22, 55, 110, 121, 242, 605 • Sum = 1184 Quit

Sociable Numbers • These are groups of three or more numbers which form closed loops • The sum of the divisors of the first give the second • The sum of the divisors of the second give third and so on until the divisors of the last give the first number Quit

Quadratic formula • The Quadratic formula works to factorise all equations of the form ax 2 + bx + c = 0 • The roots are: –––––– – b ± b – 4 ac x = ––––––– 2 a Quit

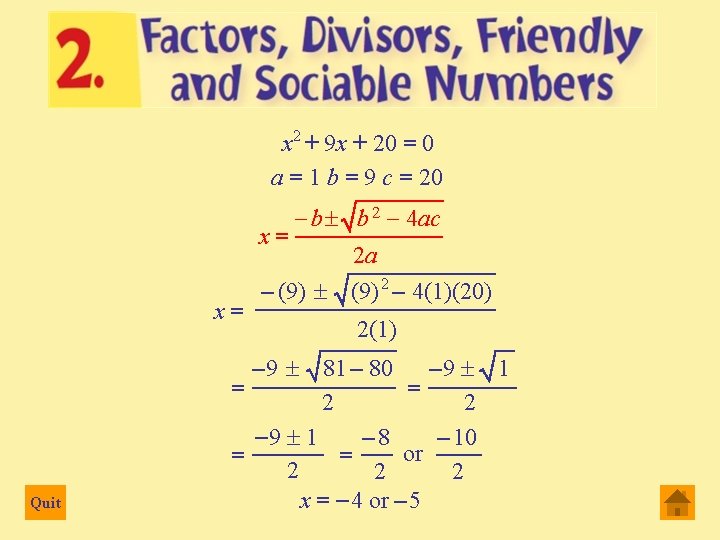
x 2 + 9 x + 20 = 0 a = 1 b = 9 c = 20 x= x= Quit - b ± b 2 - 4 ac 2 a - (9) ± (9) 2 - 4(1)(20) 2(1) -9 ± 1 -9 ± 81 – 80 = = 2 2 -9 ± 1 - 10 -8 or = = 2 2 2 x = - 4 or – 5

The area of a rectangle is 77 cm 2. One side is 4 cm longer than the other. Find the length and breadth of the rectangle. x+4 Area = 77 cm 2 x(x + 4 x) = 77 Quit x 2 + 4 x – 77 = 0 x

x 2 + 4 x – 77 = 0 a = 1 b = 4 c = – 77 x= x= - b ± b 2 - 4 ac - (4) ± (4) 2 - 4(1)(– 77) 2(1) 16 + 308 - 4 ± 324 = = 2 2 14 - 22 - 4 ± 18 or = = 2 2 2 x = 7 or – 11 -4 ± Quit 2 a

Do you want to end show? Yes No