QuineMc Cluskey Tabular Minimization Two step process utilizing

Quine-Mc. Cluskey (Tabular) Minimization Two step process utilizing tabular listings to: • • Identify prime implicants (implicant tables) Identify minimal PI set (cover tables) • • • Number of variables is not a limitation Basis for many computer implementations Don’t cares are easily handled All work is done in tabular form Proper organization and term identification are key factors for correct results

Difficulty Note: Can be 2 n minterms ~ 3 n/n primes n 3 /n 0 1 minterms 2 n 0 0 0 1 Thus O(2 n) rows and O(3 n/n ) columns AND minimum covering problem is NP-complete. Hence can probably be double exponential in size of input, i. e. difficulty is O(23 n) 2

Example x z x y xy xy y x y z w Karnaugh map z w w y zw z w x y z w Primes: y + w + x z x y z w Covering Table Solution: {1, 2} y + w is minimum prime cover. x y z w (also w + x z) 3 w x z

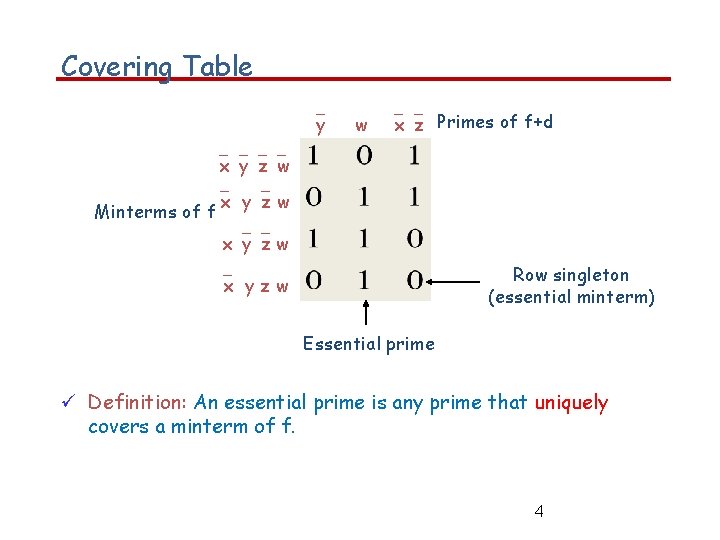
Covering Table y w x z Primes of f+d x y z w Minterms of f x y z w Row singleton (essential minterm) x y z w Essential prime Definition: An essential prime is any prime that uniquely covers a minterm of f. 4

Quine-Mc. Cluskey Minimization (cont. ) Terms are initially listed one per line in groups • • Each group contains terms with the same number of true and complemented variables Terms are listed in numerical order within group • • • full variable form cellular form 1, 0, - form Terms and implicants are identified using one of three common notations

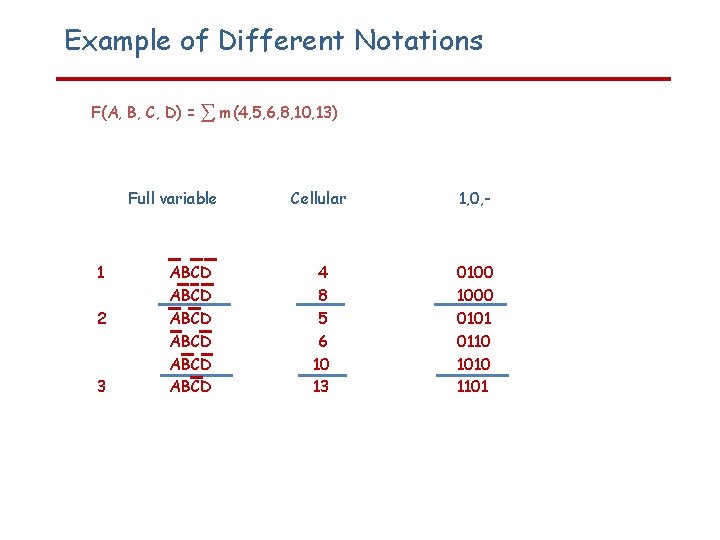
Example of Different Notations F(A, B, C, D) = m(4, 5, 6, 8, 10, 13) Full variable 1 2 3 ABCD ABCD Cellular 1, 0, - 4 8 5 6 10 13 0100 1000 0101 0110 1010 1101

Notation Forms Full variable form - variables and complements in algebraic form • • hard to identify when adjacency applies very easy to make mistakes Cellular form - terms are identified by their decimal index value • Easy to tell when adjacency applies; indexes must differ by power of two (one bit) 1, 0, - form - terms are identified by their binary index value • • • Easier to translate to/from full variable form Easy to identify when adjacency applies, one bit is different shows variable(s) dropped when adjacency is used Different forms may be mixed during the minimization

Implication Table (1, 0, -) Implication Table Quine-Mc. Cluskey Method • Tabular method to systematically Column I 0000 find all prime implicants • ƒ(A, B, C, D) = Σ m(1, 2. 5, 6, 7, 9, 10) + 0001 Σ d(0, 13, 15) 0010 • Part 1: Find all prime implicants • Step 1: Fill Column 1 with active- 0101 0110 set and DC-set minterm indices. 1001 Group by number of true 1010 variables (# of 1’s). NOTE THAT DCs ARE INCLUDED IN THIS STEP! 0111 1101 1111

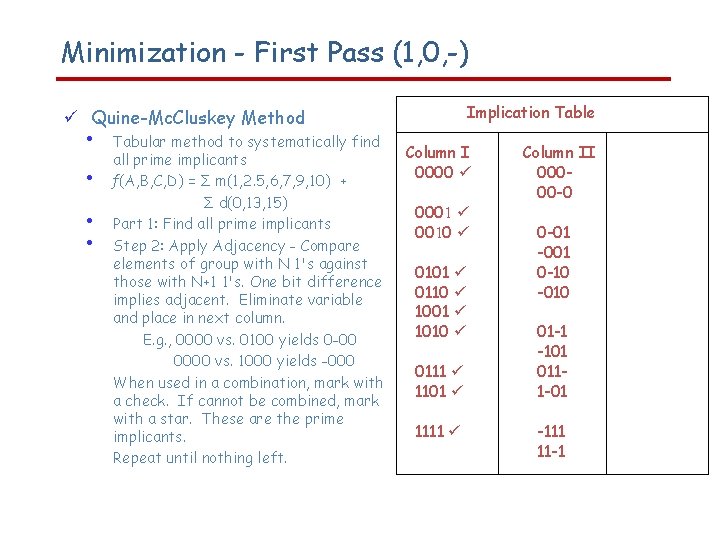
Minimization - First Pass (1, 0, -) Implication Table Quine-Mc. Cluskey Method • • Tabular method to systematically find all prime implicants ƒ(A, B, C, D) = Σ m(1, 2. 5, 6, 7, 9, 10) + Σ d(0, 13, 15) Part 1: Find all prime implicants Step 2: Apply Adjacency - Compare elements of group with N 1's against those with N+1 1's. One bit difference implies adjacent. Eliminate variable and place in next column. E. g. , 0000 vs. 0100 yields 0 -00 0000 vs. 1000 yields -000 When used in a combination, mark with a check. If cannot be combined, mark with a star. These are the prime implicants. Repeat until nothing left. Column I 0000 0001 0010 0101 0110 1001 1010 0111 1101 1111 Column II 00000 -0 0 -01 -001 0 -10 -010 01 -1 -101 0111 -01 -111 11 -1

Minimization - Second Pass (1, 0, -) Quine-Mc. Cluskey Method • Step 2 cont. : Apply Adjacency Compare elements of group with N 1's against those with N+1 1's. One bit difference implies adjacent. Eliminate variable and place in next column. E. g. , 0000 vs. 0100 yields 0 -00 00 -0 vs. 10 -0 yields -0 -0 When used in a combination, mark with a check. If cannot be combined, mark with a star. THESE ARE THE PRIME IMPLICANTS. Repeat until nothing left. The set of constitutes the Complete Sum c Implication Table Column I 0000 0001 0010 0101 0110 1001 1010 0111 1101 1111 Column II 000 - * 00 -0 * 0 -01 -001 0 -10 -010 * * 01 -1 -101 011 - * 1 -01 -111 11 -1 Column III - -01 * - 1 -1 *

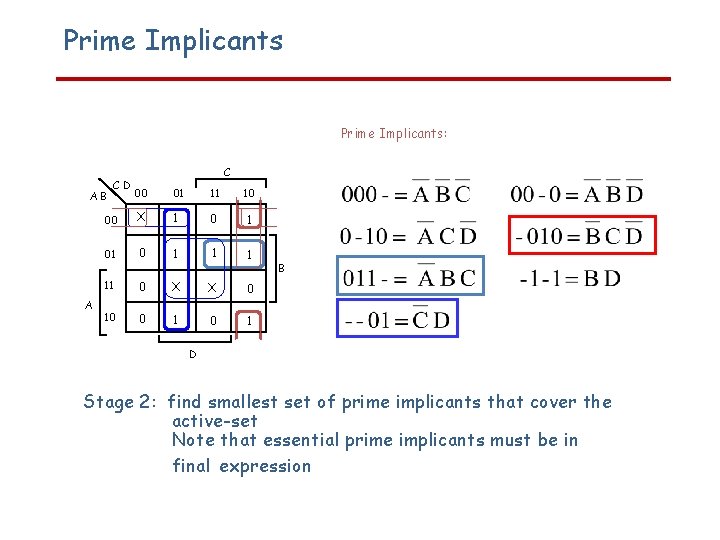
Prime Implicants: C 00 01 11 10 00 X 1 01 0 1 11 0 X X 0 10 0 1 AB A CD B D Stage 2: find smallest set of prime implicants that cover the active-set Note that essential prime implicants must be in final expression

Coverage Table Coverage Chart 1 X 2 0, 1 000 - 0, 2 00 -0 X 2, 6 0 -10 X 2, 10 -010 X 6, 7 011 - 1, 5, 9, 13 --01 5, 7, 13, 15 -1 -1 5 6 9 10 X X 7 X X NOTE: DON’T INCLUDE DCs IN COVERAGE TABLE; THEY DON’T HAVE COVERED BY THE FINAL LOGIC EXPRESSION! X rows = prime implicants columns = ON-set elements (minterms) place an "X" if ON-set element is covered by the prime implicant

Row and Column Dominance Definition: Given two rows i 1 and i 2, a row i 1 is said to dominate i 2 if it has checks in all columns in which i 2 has checks, i. e. it is a superset of i 2 Example: i 1 i 2 xx xx i 1 dominates i 2 We can remove row i 2, because we would never choose i 2 in a minimum cover since it can always be replaced by i 1 (i 2 is anymore a prime implicant). DOMINATED ROWS CAN BE ELIMINATED 14

Row and Column Dominance Definition: Given two colums j 1 and j 2, if the set of primes of column j 2 is contained in the set of primes of column j 1 is said to be dominated by j 1. Example: j 1 dominates j 2 j 1 x j 2 x x x We can remove column j 1 since we have to choose a prime to cover j 2, any such prime also covers j 1, that would result covered as well. DOMINATING COLUMNS CAN BE ELIMINATED 15

Pruning the Covering Table 1. Remove all rows covered by essential primes (columns in row singletons). Put these primes in the cover G. 2. Group identical rows together and remove dominated rows. 3. Remove dominating columns. For equal columns, keep just one to represent them. 4. Newly formed row singletons define n-ary essential primes. 5. Go to 1 if covering table decreased. The algorithm may terminate successfully with a set of primes and an emty table. In case it terminate with a non empty table, the resulting reduced covering table is called the cyclic core. This has to be solved. A minimum solution for the cyclic core must be added to the resulting G. 16

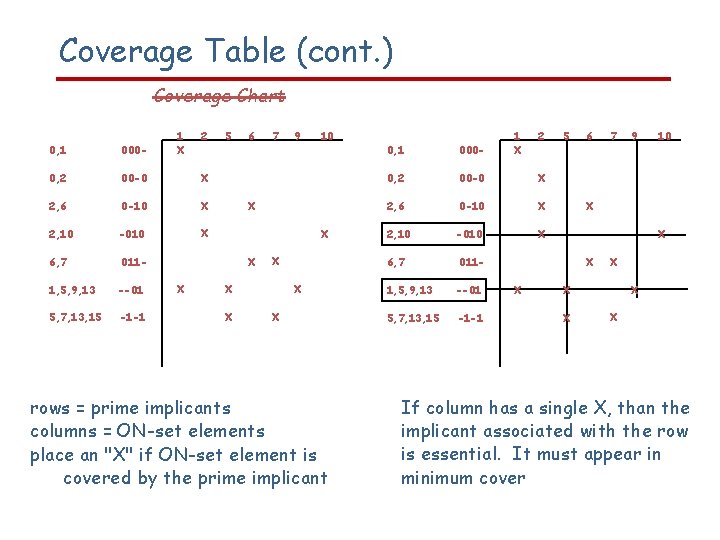
Coverage Table (cont. ) Coverage Chart 1 X 2 0, 1 000 - 0, 2 00 -0 X 2, 6 0 -10 X 2, 10 -010 X 6, 7 011 - 1, 5, 9, 13 --01 5, 7, 13, 15 -1 -1 5 6 9 10 X X 7 X X X rows = prime implicants columns = ON-set elements place an "X" if ON-set element is covered by the prime implicant 1 X 2 0, 1 000 - 0, 2 00 -0 X 2, 6 0 -10 X 2, 10 -010 X 6, 7 011 - 1, 5, 9, 13 --01 5, 7, 13, 15 -1 -1 5 6 9 10 X X 7 X X X If column has a single X, than the implicant associated with the row is essential. It must appear in minimum cover

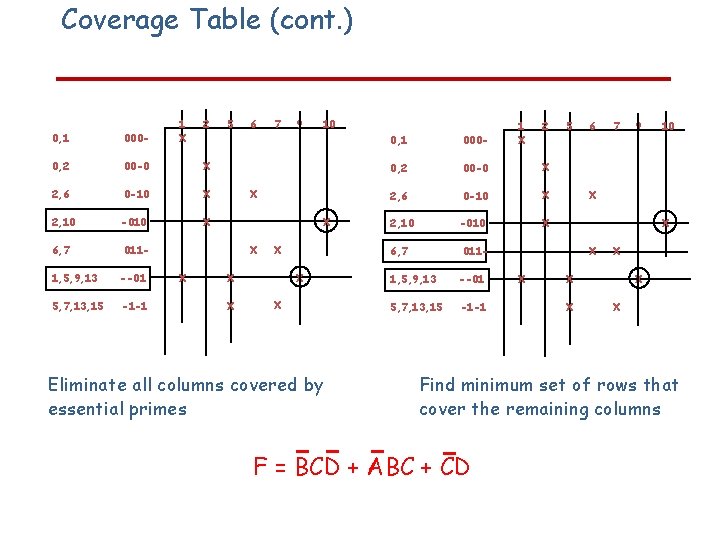
Coverage Table (cont. ) 1 X 2 0, 1 000 - 0, 2 00 -0 X 2, 6 0 -10 X 2, 10 -010 X 6, 7 011 - 1, 5, 9, 13 --01 5, 7, 13, 15 -1 -1 5 6 9 10 X X 7 X X X Eliminate all columns covered by essential primes 1 X 2 0, 1 000 - 0, 2 00 -0 X 2, 6 0 -10 X 2, 10 -010 X 6, 7 011 - 1, 5, 9, 13 --01 5, 7, 13, 15 -1 -1 5 6 9 10 X X 7 X X X Find minimum set of rows that cover the remaining columns F = BCD + ABC + CD

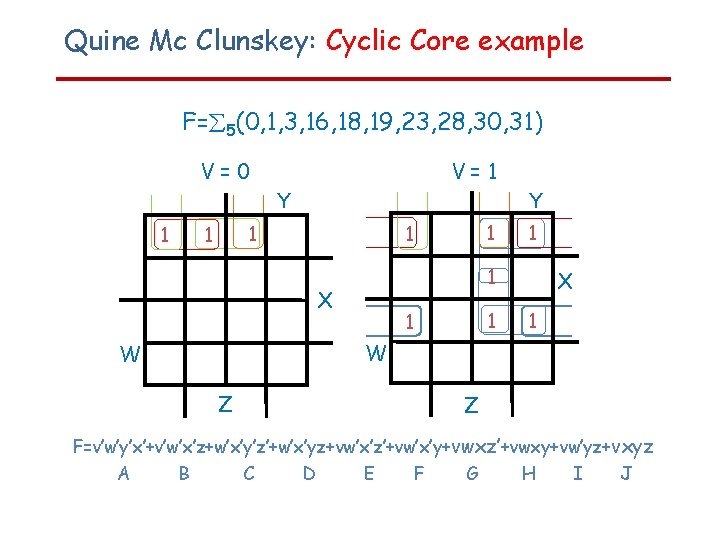
Quine Mc Clunskey: Cyclic Core example F= 5(0, 1, 3, 16, 18, 19, 23, 28, 30, 31) V=0 V=1 Y 1 1 1 X 1 W W Z Z F=v’w’y’x’+v’w’x’z+w’x’y’z’+w’x’yz+vw’x’z’+vw’x’y+vwxz’+vwxy+vw’yz+vxyz A B C D E F G H I J

Implication Table (1, 0, -) Quine-Mc. Cluskey Method • • Tabular method to systematically find all prime implicants ƒ(v, w, x, y, z) = Σm(0, 1, 3, 16, 18, 19, 23, 28, 30, 31) Part 1: Find all prime implicants Step 1: Fill Column 1 with activeset and DC-set minterm indices. Group by number of true variables (# of 1’s). Implication Table Column I 00000 0 0 001 1 0000 0 0 01 1 1 0 01 0 1 00 1 1 10 0 10 1 1 11 1 0 1 1 11 1 Column II 0000 - * -0000 * A: 0 1 C: 0 16 000 -1 * 100 -0 * B: 1 3 E: 16 18 -0011 * 1001 - * D: 3 19 F: 18 19 10 -11 * 111 -0 * I: 19 23 G: 28 30 1 -111 * 1111 - * J: 23 31 H: 30 31 F=v’w’y’x’+v’w’x’z+w’x’y’z’+w’x’yz+vw’x’z’+vw’x’y+vwxz’+vwxy+vw’yz+vxyz A B C D E F G H I J

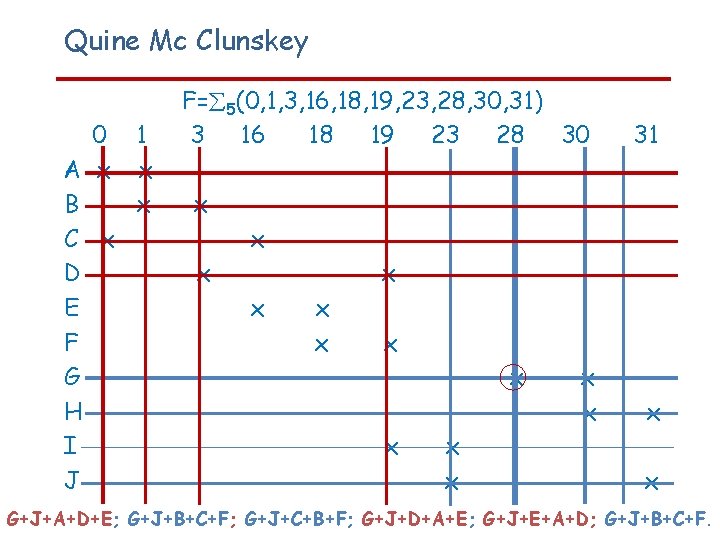
Quine Mc Clunskey 0 1 A x x B x C x D E F G H I J F= 5(0, 1, 3, 16, 18, 19, 23, 28, 30, 31) 3 16 18 19 23 28 30 31 x x x x G+J+A+D+E; G+J+B+C+F; G+J+C+B+F; G+J+D+A+E; G+J+E+A+D; G+J+B+C+F.

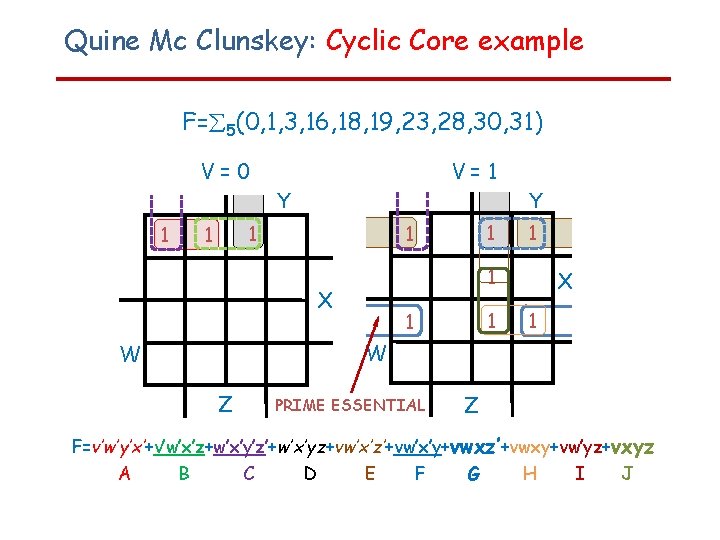
Quine Mc Clunskey: Cyclic Core example F= 5(0, 1, 3, 16, 18, 19, 23, 28, 30, 31) V=0 V=1 Y 1 1 1 X 1 W W Z PRIME ESSENTIAL Z F=v’w’y’x’+v’w’x’z+w’x’y’z’+w’x’yz+vw’x’z’+vw’x’y+vwxz’+vwxy+vw’yz+vxyz A B C D E F G H I J

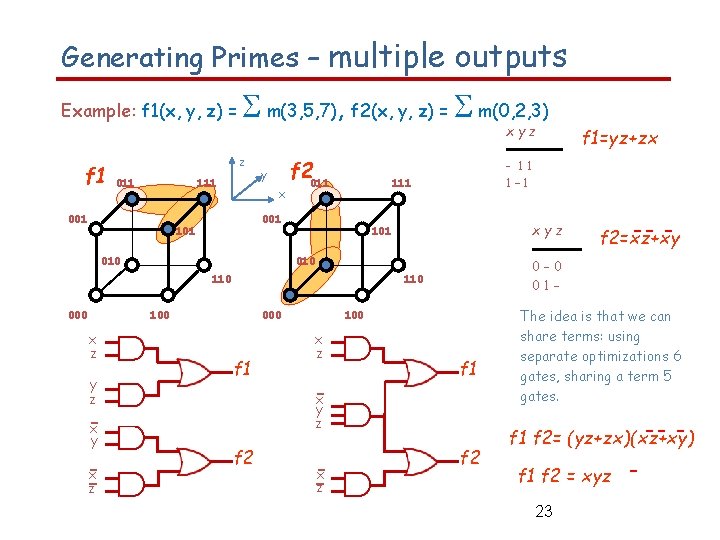
Generating Primes – multiple outputs Example: f 1(x, y, z) = f 1 m(3, 5, 7), f 2(x, y, z) = m(0, 2, 3) xyz z 011 111 001 y x f 2011 010 y z – x y – x – z 000 f 1 f 2 100 x z – x y z – x – z -- f 2=xz+xy 0– 0 01– 110 100 x z xyz 101 110 000 - 11 1– 1 111 001 101 f 1=yz+zx f 1 f 2 The idea is that we can share terms: using separate optimizations 6 gates, sharing a term 5 gates. -- f 1 f 2= (yz+zx)(xz+xy) f 1 f 2 = xyz 23 -

Generating Primes – multiple outputs Theorem: if p 1 is a prime implicant for f 1, and p 2 is a prime implicant for f 2, then if p 1. p 2 0, p 1. p 2 is a prime implicant of f 1. f 2 Theorem: if p 3 is a prime implicant for f 1. f 2, then there exist p 1 for f 1, and p 2 for f 2, such that p 3=p 1. p 2 We can conclude that all prime implicants of f 1. f 2, are minimal sharable products for f 1 and f 2: and that all prime implicants for f 1. f 2 are created by products of prime implicants for f 1. f 2 The way to use this is to make the prime implicants of f 1. f 2 available to the minimizations of f 1 and f 2 by extending the table concept 24

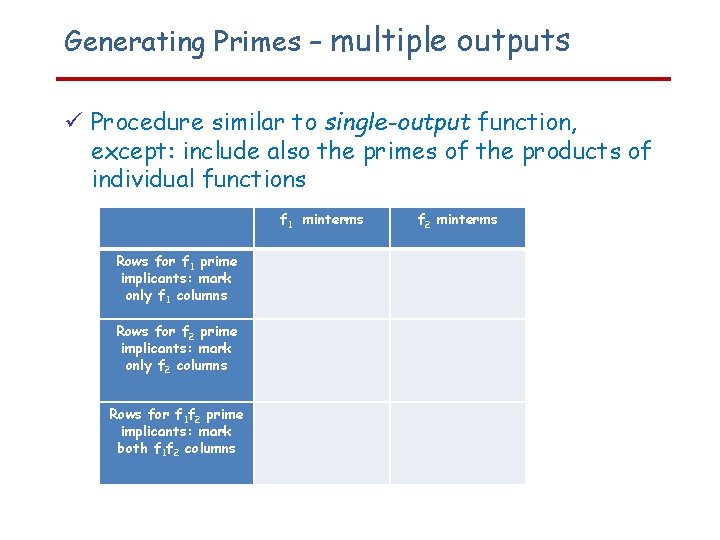
Generating Primes – multiple outputs Procedure similar to single-output function, except: include also the primes of the products of individual functions f 1 minterms Rows for f 1 prime implicants: mark only f 1 columns Rows for f 2 prime implicants: mark only f 2 columns Rows for f 1 f 2 prime implicants: mark both f 1 f 2 columns f 2 minterms

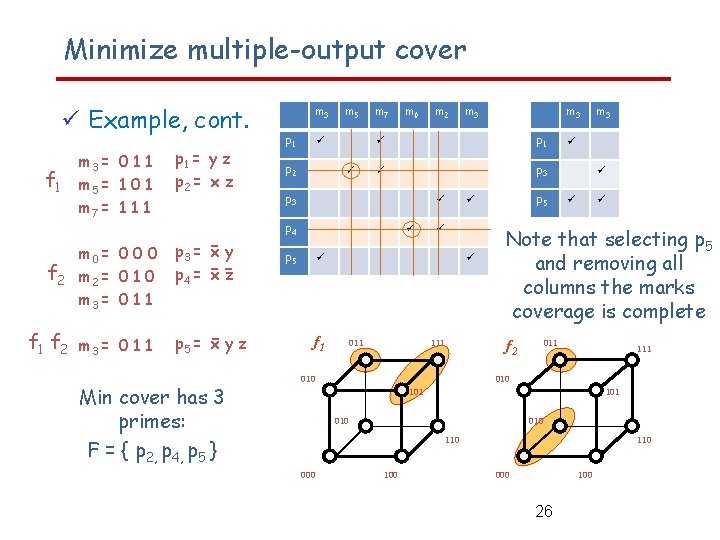
Minimize multiple-output cover Example, cont. f 1 m 3 = 0 1 1 m 5 = 1 0 1 m 7 = 1 1 1 m 0 = 0 0 0 f 2 m 2 = 0 1 0 m 3 = 0 1 1 f 2 m 3 = 0 1 1 p 1 = y z p 2 = x z -- p 3 = x y p 4 = x z - p 5 = x y z Min cover has 3 primes: F = { p 2, p 4, p 5 } m 3 p 1 m 5 p 2 m 7 m 0 m 2 p 1 p 3 p 4 011 p 5 f 1 m 3 p 5 m 3 010 Note that selecting p 5 and removing all columns the marks coverage is complete f 2 111 011 111 010 101 010 110 000 m 3 100 110 000 100 26