Quick Sort Merge Sort Contents Divide Conquer Strategy

Quick Sort & Merge Sort

Contents �Divide & Conquer Strategy �Merge Sort & Quick Sort Algorithms �Merge Sort & Quick Sort Examples �Merge Sort & Quick Sort Analysis �Merge Sort & Quick Sort Applications

Divide And Conquer �Steps Involved in Divide and Conquer Step 1: Divide the problem into a number of sub problems that are smaller instances of the same problem. Step 2: Conquer the sub problems by solving Recursively. If the sub problem size are small enough however just solve the sub problems in a straightforward manner Step 3: Combine the solutions to the sub problems into the solution of origional Problem.

Merge Sort �Steps involved in Merge Sort Algorithm: 1. Divide the n-element sequence to be sorted into two subsequences of n/2 elements. 2. Sort the two subsequences recursively using merge sort (Recursive Case). The Recursion bottoms out when the sequence to be sorted has length 1. 3. Merge the two sorted subsequences to sort the n-element Sequence.

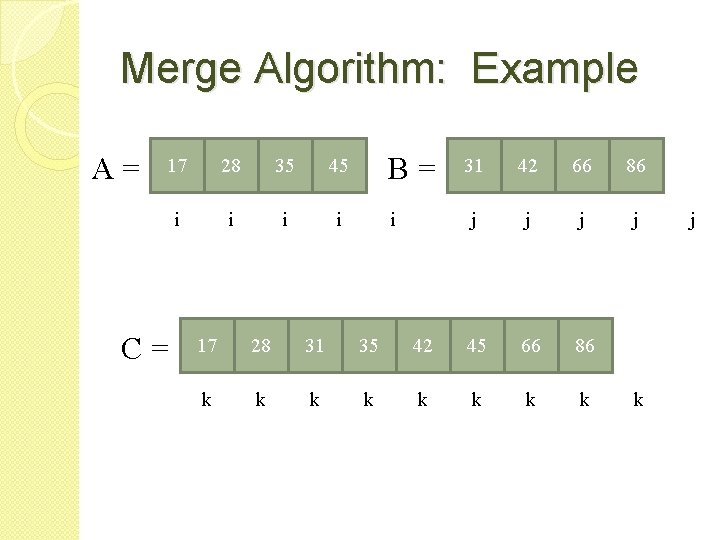
Merge Algorithm[2] Algorithm Merge(low, mid, high) { i=low, k=low, j=mid+1; while((i <= mid) and (j <= high) )do { if(a[i] <= a[j]) then b[k]=a[i], i++; else b[k]=a[j], j++; k++; } if(k > mid) then for(l=j to high) do b[i]=a[l], i++; else for(l=h to mid) do b[i]=a[l], i++; for(l=low to high) do a[l] = b[l]; }

Merge Algorithm: Example A= 17 28 35 45 i i C= B= i 31 42 66 86 j j 17 28 31 35 42 45 66 86 k k k k k j

Merge Sort: Algorithm[2] Algorithm Merge. Sort(low, high) { if(low < high) then { mid = (low+high)/2; Merge. Sort(low, mid); Merge. Sort(mid+1, high); Merge(low, mid, high); } }

Merge Sort: Example 31 28 31 17 17 32 66 42 35 45 42 66 86 86 45 31 28 31 17 17 66 31 31 28 28 31 28 35 42 45 86 86 45 17 66 35 42 86 86 45 45 86 45

Merge Sort: Analysis The Recurrenc relation for Merge Sort is T(n) = 2 T(n/2) + n ……. For n >1 = 1 ………………. For n = 1 We Assume n = 2 k T(n) = 2[2 T(n/4) + n/2] + n = 4 T(n/4) + 2 n = 22 T(n/22) + 2 n = 22[2 T(n/8)+ n/4] + 2 n = 23 T(n/23) + 3 n = 24 T(n/24) + 4 n. . = 2 j. T(n/2 j) + jn……. . Equation 1

Now T(1) = T(n/2 j) = 1 1= n/2 j n= 2 j j = log 2 n Substituting values in equation 1 T(n) = n*1 + n log 2 n = O(n log 2 n)

Quick Sort �Chose a Pivot element �Partition A into lower & Upper parts with respect to the pivot. �Recursively sort the two Partitions. �Combining the solution is not needed.

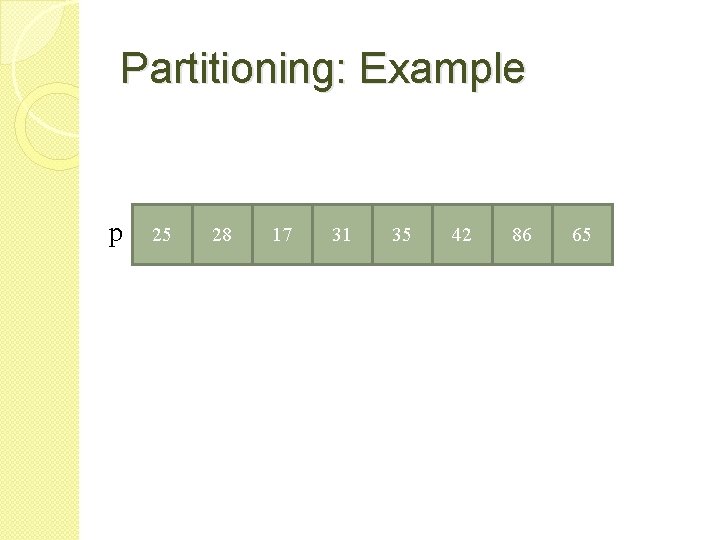
Partitioning Algorithm Partition(a, m, p) { p = a[m], i = m, j = p; repeat { repeat i++; until(a[i] >=p); repeat j--; until(a[j]<=p); if(i<j) then swap(a, i, j); }until(i>=j); a[m] = a[j], a[j] = p; return j; }

Partitioning: Example p 31 25 28 17 65 25 31 35 42 86 25 65

Quick Sort: Algorithm Quick. Sort(p, q) { if(p < q) then { j = partition(a, p, q+1); Quick. Sort(p, j-1); Quick. Sort(j+1, q); //No need to combine Solutions } }

Quick Sort: Analysis �Best Case: if Pivot is median, then each partition will be of size n/2 so recurrence relation will be , T(n) = 2 T(n/2) + n = nlog(n) �Worst Case: if Pivot is always maximum or minimum element in the partition (i. e. partition is already sorted in ascending or descending order), then one partition will be empty and other will containn (n-1) elements

Applications � 1. Databases � 2. Counting Number of Inversions

References S. K. Srivastava, Deepali Srivastava, “Data Structures Through C in Depth”, BPB Publications. 2. Ellis Horowitz, Sartaz Sahni, Sanguthevar Rajasekaran “Fundamentals of Algorithms”, University Press. 3. Cormen, Leiserson, Rivest, “Algorithms”, PHI. 4. Madhavan Mukund, “Design & Analysis of Algorithms”, NPTEL Video Lectures 1.