Queueing Networks with Infinite Virtual Queues An Example

Queueing Networks with Infinite Virtual Queues An Example, An Application and a Fundamental Question Yoni Nazarathy (Supervisor: Prof. Gideon Weiss) University of Haifa STUDENTS PROBABILITY DAY Weizmann Institute of Science March 28, 2007

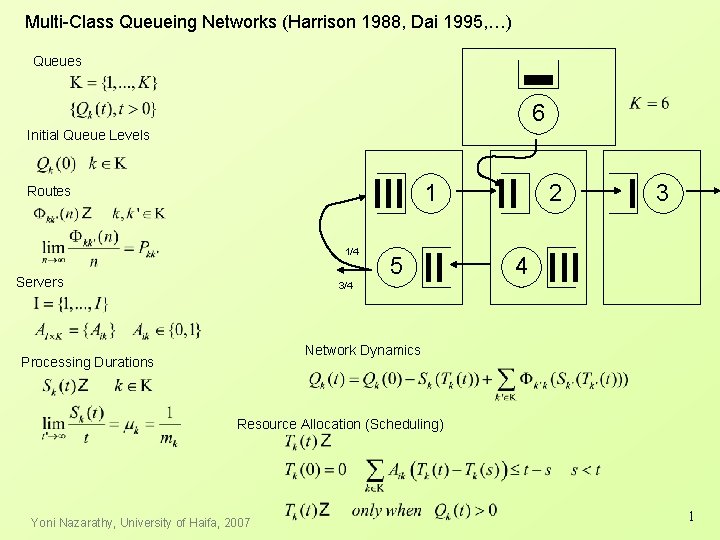
Multi-Class Queueing Networks (Harrison 1988, Dai 1995, …) Queues 6 Initial Queue Levels 1 Routes 1/4 Servers 5 2 3 4 3/4 Network Dynamics Processing Durations Resource Allocation (Scheduling) Yoni Nazarathy, University of Haifa, 2007 1

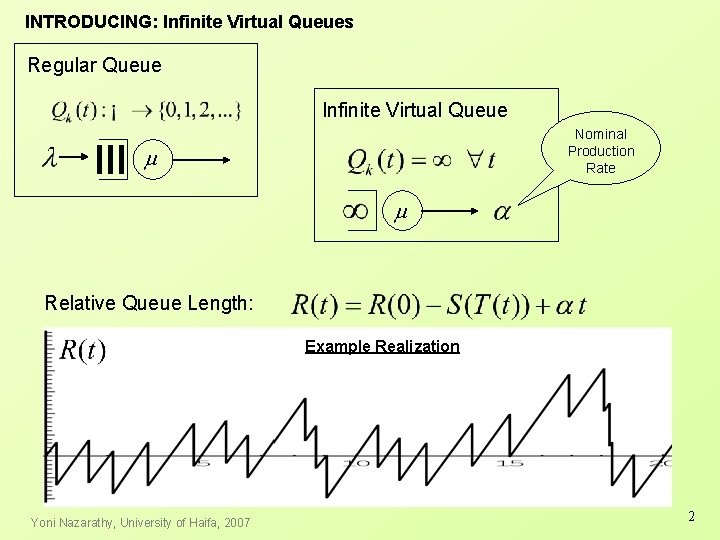
INTRODUCING: Infinite Virtual Queues Regular Queue Infinite Virtual Queue Nominal Production Rate m m Relative Queue Length: Example Realization Yoni Nazarathy, University of Haifa, 2007 2

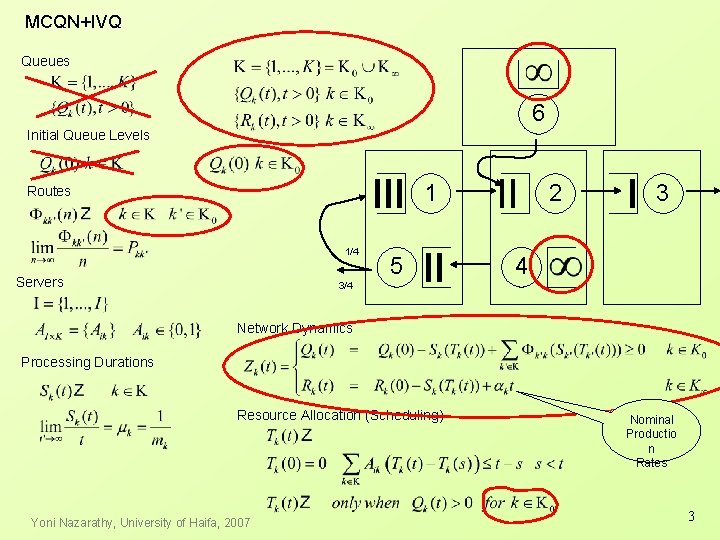
MCQN+IVQ Queues 6 Initial Queue Levels 1 Routes 1/4 Servers 5 2 3 4 3/4 Network Dynamics Processing Durations Resource Allocation (Scheduling) Yoni Nazarathy, University of Haifa, 2007 Nominal Productio n Rates 3

An Example Yoni Nazarathy, University of Haifa, 2007 4

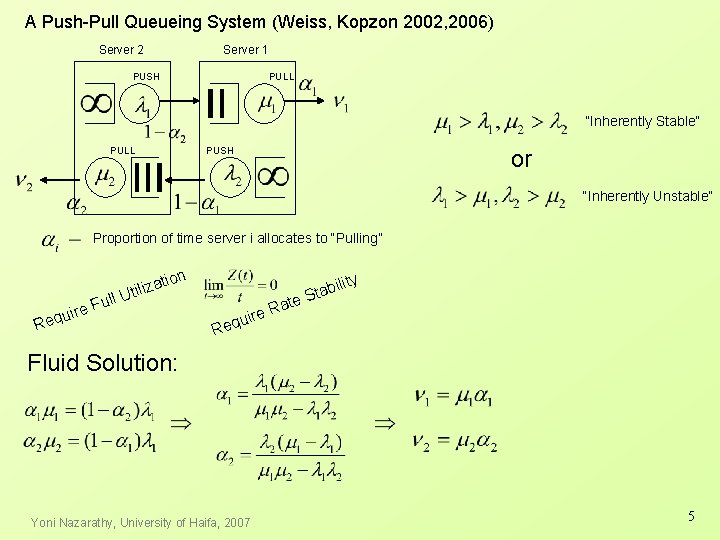
A Push-Pull Queueing System (Weiss, Kopzon 2002, 2006) Server 2 Server 1 PUSH PULL “Inherently Stable” PULL PUSH or “Inherently Unstable” Proportion of time server i allocates to “Pulling” ion e. F r i u q ull zat i l i t U Re ate R e quir y bilit a t S Re Fluid Solution: Yoni Nazarathy, University of Haifa, 2007 5

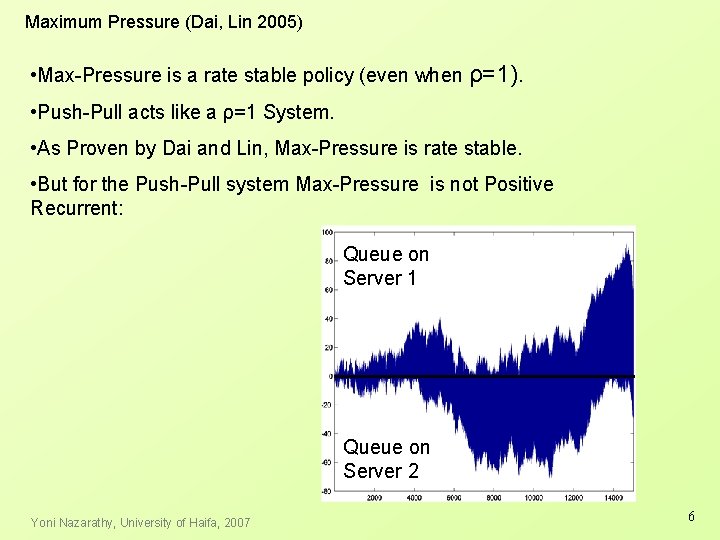
Maximum Pressure (Dai, Lin 2005) • Max-Pressure is a rate stable policy (even when ρ=1). • Push-Pull acts like a ρ=1 System. • As Proven by Dai and Lin, Max-Pressure is rate stable. • But for the Push-Pull system Max-Pressure is not Positive Recurrent: Queue on Server 1 Queue on Server 2 Yoni Nazarathy, University of Haifa, 2007 6

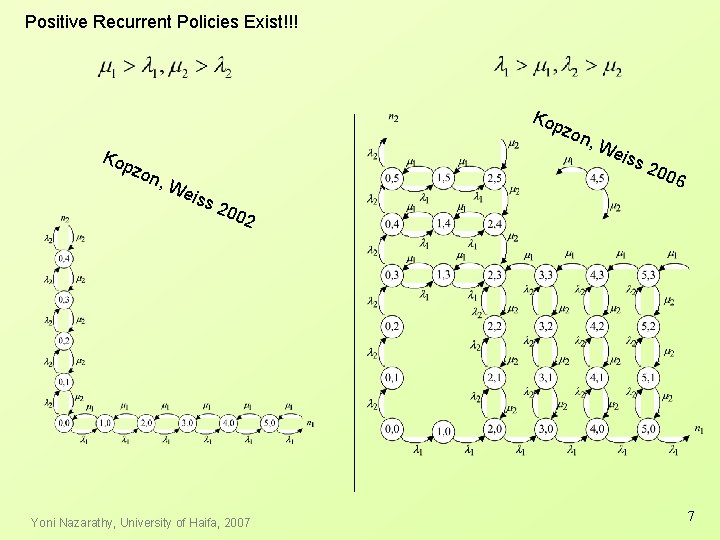
Positive Recurrent Policies Exist!!! Kop z on , on, We iss 200 6 200 2 Yoni Nazarathy, University of Haifa, 2007 7

An Application Yoni Nazarathy, University of Haifa, 2007 8

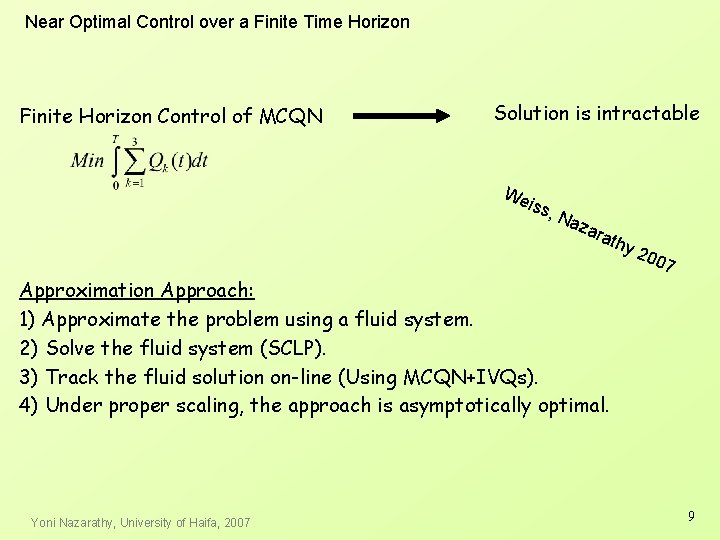
Near Optimal Control over a Finite Time Horizon Finite Horizon Control of MCQN Solution is intractable We iss, Na zar ath y 2 007 Approximation Approach: 1) Approximate the problem using a fluid system. 2) Solve the fluid system (SCLP). 3) Track the fluid solution on-line (Using MCQN+IVQs). 4) Under proper scaling, the approach is asymptotically optimal. Yoni Nazarathy, University of Haifa, 2007 9

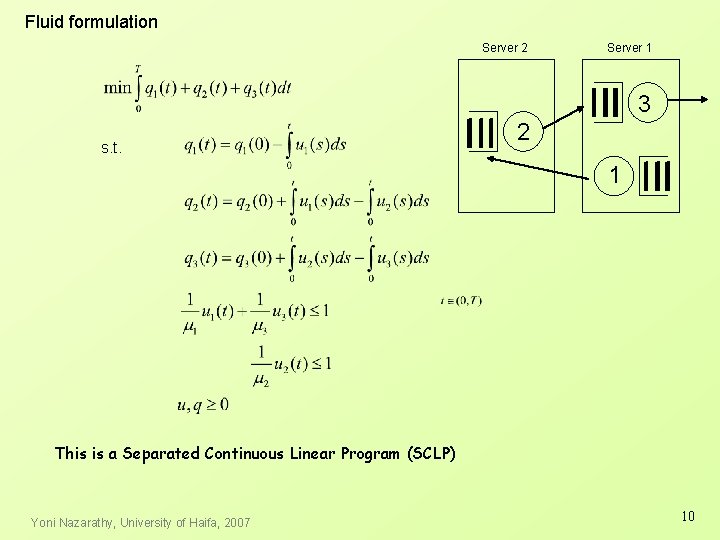
Fluid formulation Server 2 Server 1 3 s. t. 2 1 This is a Separated Continuous Linear Program (SCLP) Yoni Nazarathy, University of Haifa, 2007 10

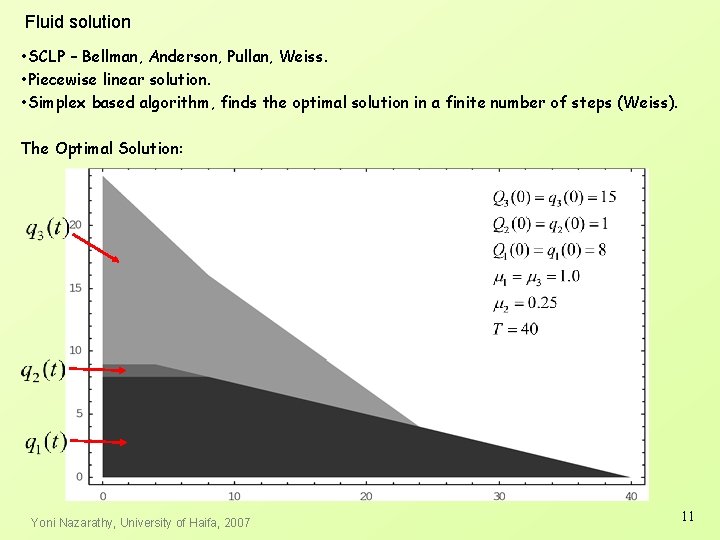
Fluid solution • SCLP – Bellman, Anderson, Pullan, Weiss. • Piecewise linear solution. • Simplex based algorithm, finds the optimal solution in a finite number of steps (Weiss). The Optimal Solution: Yoni Nazarathy, University of Haifa, 2007 11

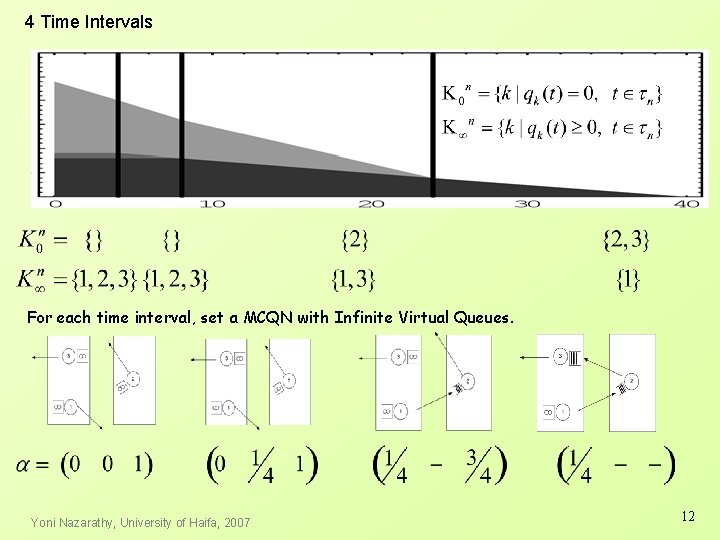
4 Time Intervals For each time interval, set a MCQN with Infinite Virtual Queues. Yoni Nazarathy, University of Haifa, 2007 12

Now Con Maximum trol the M Pressure CQN+IVQ (Dai, Lin) Yoni Nazarathy, University of Haifa, 2007 Using a R a is such a te Stable Policy policy, ev en when ρ =1 13

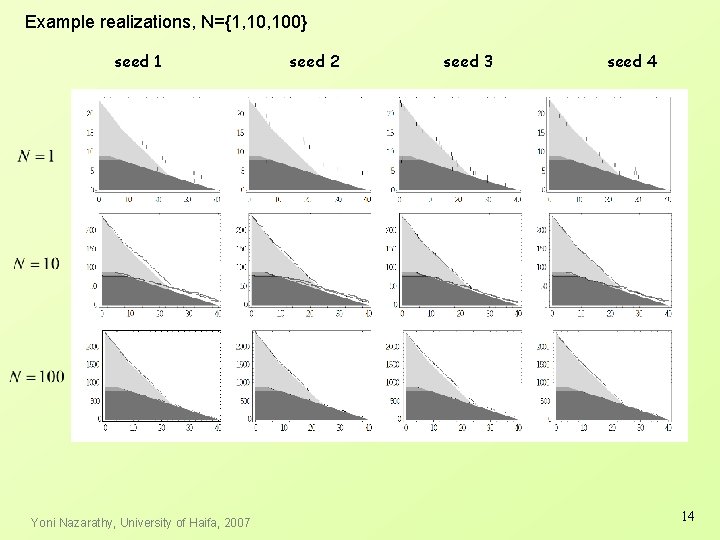
Example realizations, N={1, 100} seed 1 Yoni Nazarathy, University of Haifa, 2007 seed 2 seed 3 seed 4 14

A Fundamental Question Yoni Nazarathy, University of Haifa, 2007 15

Is there a characterization of MCQN+IVQs that allows: • Full Utilization of all the servers that have an IVQ. • Stability of all finite queues. • Proportional equality among production streams. ? Yoni Nazarathy, University of Haifa, 2007 16

Thank You Yoni Nazarathy, University of Haifa, 2007 17