Queue C and Data Structures Baojian Hua bjhuaustc

Queue C and Data Structures Baojian Hua bjhua@ustc. edu. cn

Linear List n Recall that a linear list has the form: n n The delete and insert operations may insert or delete an arbitrary element e_i If the delete is restricted at one end and insert at the other end, we get a queue

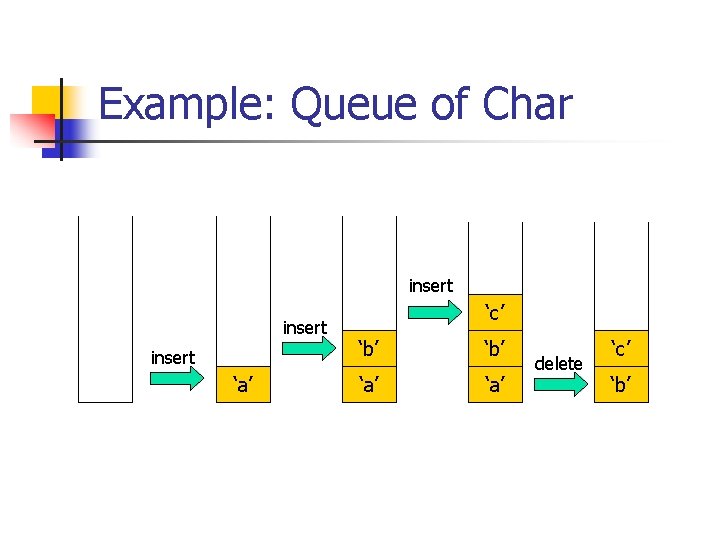
Example: Queue of Char insert ‘a’ ‘c’ ‘b’ ‘a’ delete ‘c’ ‘b’

Abstract Data Types in C: Interface // in file “queue. h” #ifndef QUEUE_H #define QUEUE_H typedef struct Queue_t *Queue_t; Queue_t Queue_new (); int Queue_size (Queue_t q); int Queue_is. Empty (Queue_t q); void Queue_en. Queue (Queue_t q, poly x); poly Queue_de. Queue (Queue_t q); poly Queue_get. Head (Queue_t q); #endif

Implementation Using Extensible Array // in file “array. Queue. c” #include “queue. h” struct Queue_t { Array_t l; }; // Recall the box strategy: q l

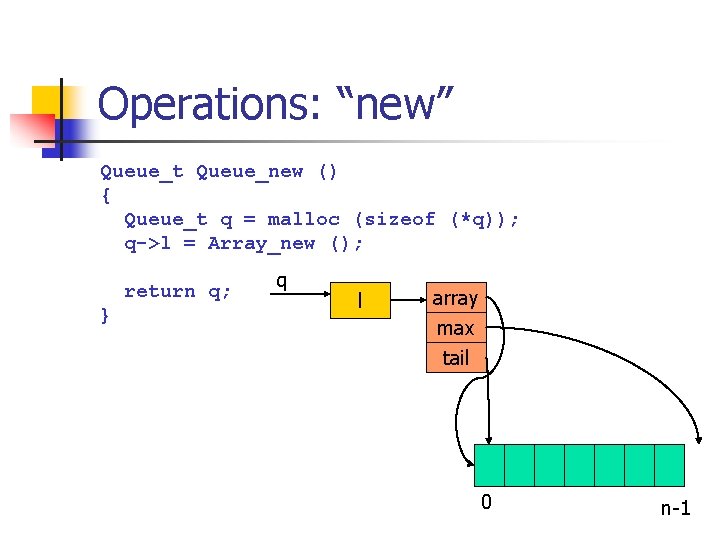
Operations: “new” Queue_t Queue_new () { Queue_t q = malloc (sizeof (*q)); q->l = Array_new (); return q; } q l array max tail 0 n-1

Operations: “size” int Queue_size (Queue_t q) { return Array_length (q->l); } q l array max tail 0 n-1

Operations: “is. Empty” int Queue_is. Empty (Queue_t q) { return Array_is. Empty (q->l); } q l array max tail 0 n-1

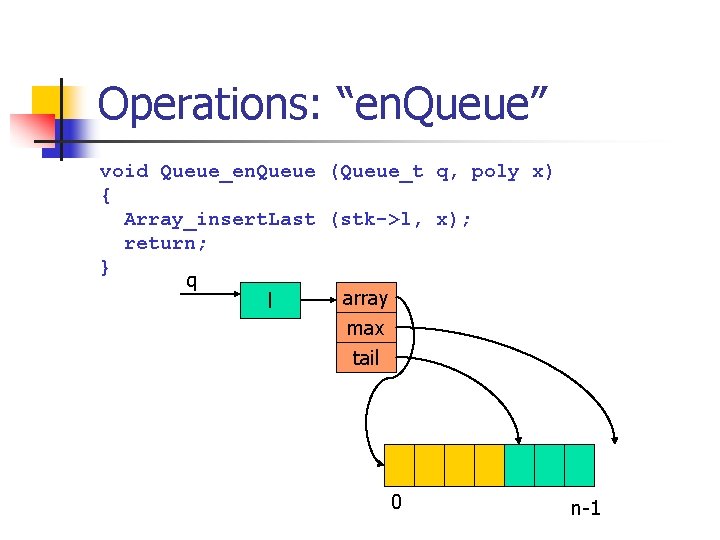
Operations: “en. Queue” void Queue_en. Queue (Queue_t q, poly x) { Array_insert. Last (stk->l, x); return; } q array l max tail 0 n-1

Operations: “de. Queue” poly Queue_de. Queue (Queue_t q) { if (Array_is. Empty (q->l)) error (“empty queue”); return Array_delete. First (q->l); }

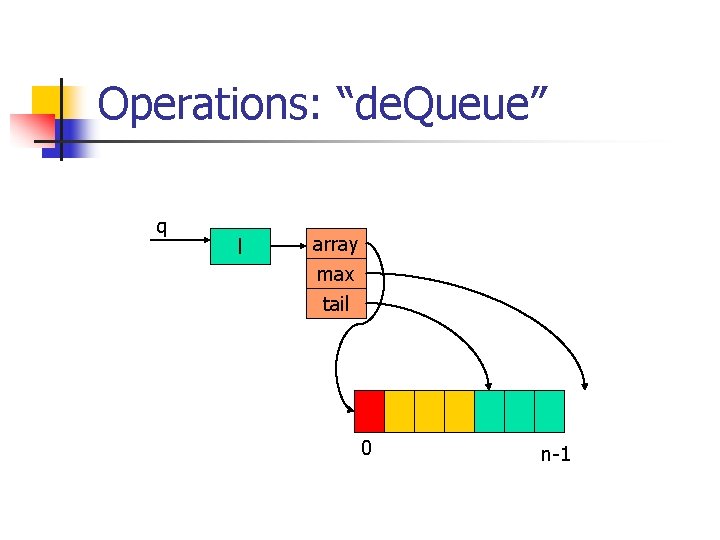
Operations: “de. Queue” q l array max tail 0 n-1

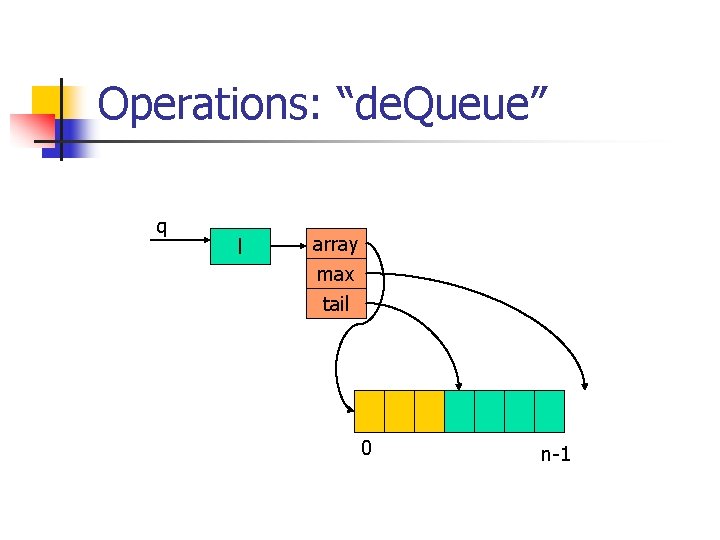
Operations: “de. Queue” q l array max tail 0 n-1

Analysis n What’s the complexity? n n en. Queue: O(1) de. Queue: O(n) n n data movement Can we do better? n Lazy approach n n better amortized performance Circular queue

Lazy Approach n Instead of moving data when “de. Queue”, we move data only when “en. Queue” reaching the tail of the queue n n O(n) on n operations which has O(1) amortized cost

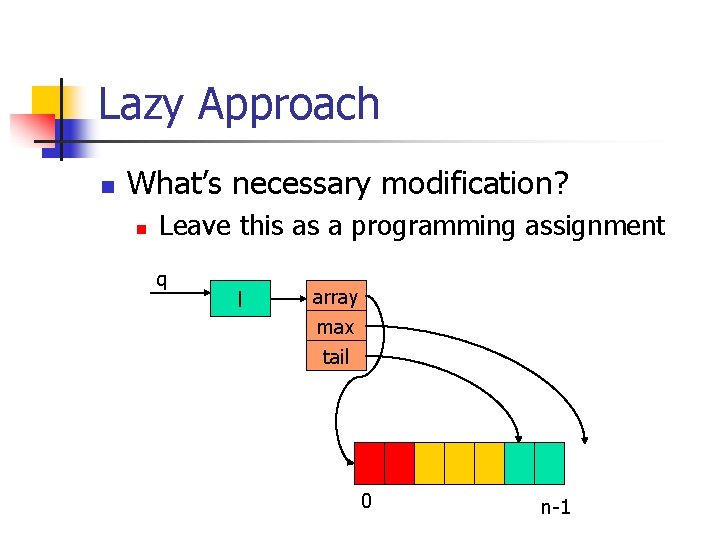
Lazy Approach n What’s necessary modification? n Leave this as a programming assignment q l array max tail 0 n-1

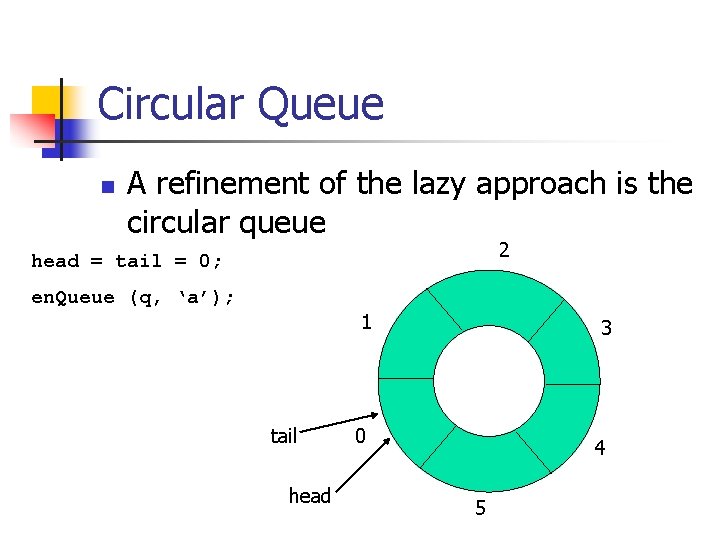
Circular Queue n A refinement of the lazy approach is the circular queue 2 head = tail = 0; en. Queue (q, ‘a’); 1 tail head 3 0 4 5

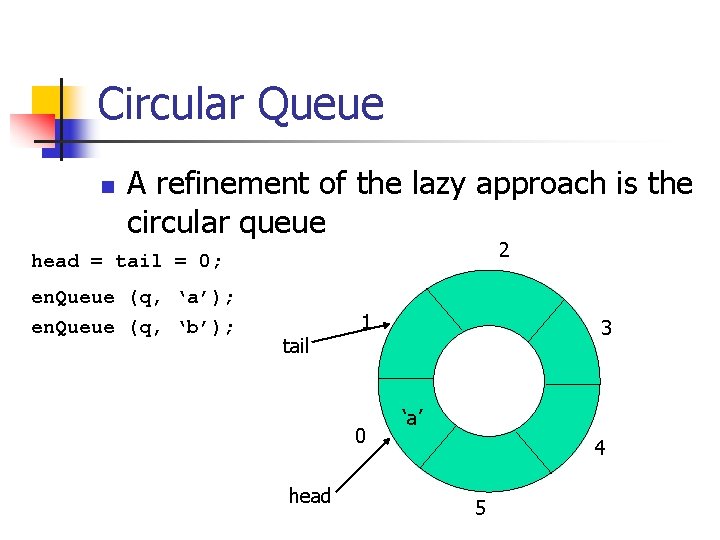
Circular Queue n A refinement of the lazy approach is the circular queue 2 head = tail = 0; en. Queue (q, ‘a’); en. Queue (q, ‘b’); tail 1 0 head 3 ‘a’ 4 5

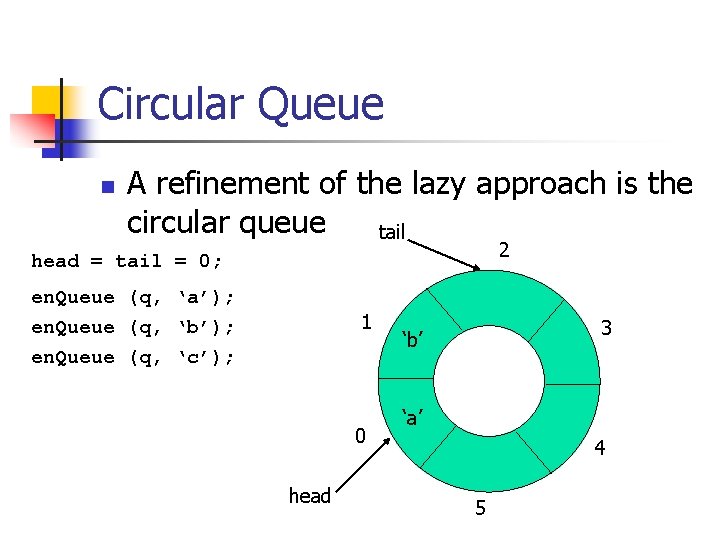
Circular Queue n A refinement of the lazy approach is the circular queue tail 2 head = tail = 0; en. Queue (q, ‘a’); en. Queue (q, ‘b’); en. Queue (q, ‘c’); 1 0 head 3 ‘b’ ‘a’ 4 5

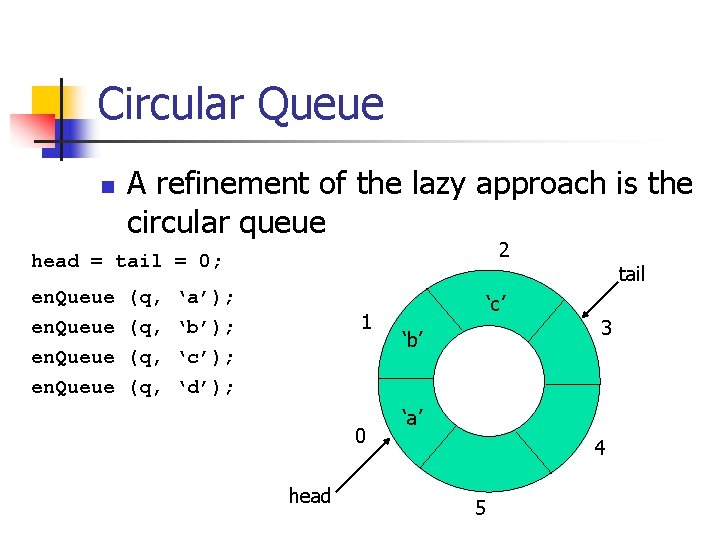
Circular Queue n A refinement of the lazy approach is the circular queue 2 head = tail = 0; en. Queue (q, (q, ‘a’); ‘b’); ‘c’); ‘d’); 1 0 head ‘c’ ‘b’ tail 3 ‘a’ 4 5

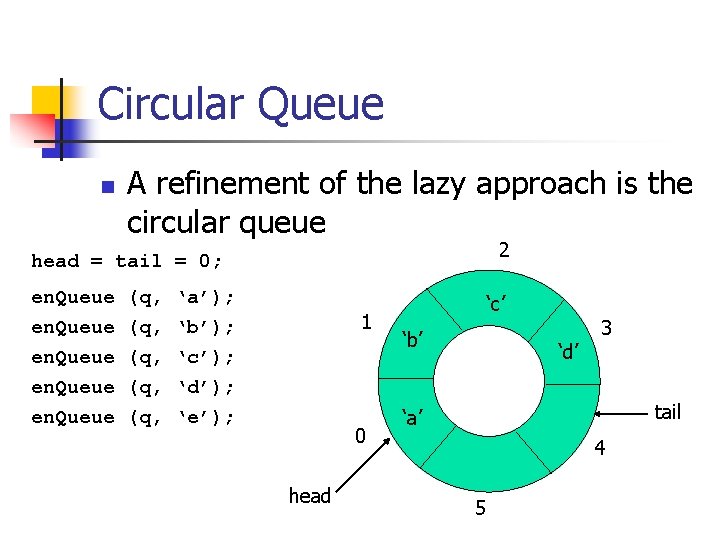
Circular Queue n A refinement of the lazy approach is the circular queue 2 head = tail = 0; en. Queue (q, (q, (q, ‘a’); ‘b’); ‘c’); ‘d’); ‘e’); 1 0 head ‘c’ ‘b’ ‘d’ 3 tail ‘a’ 4 5

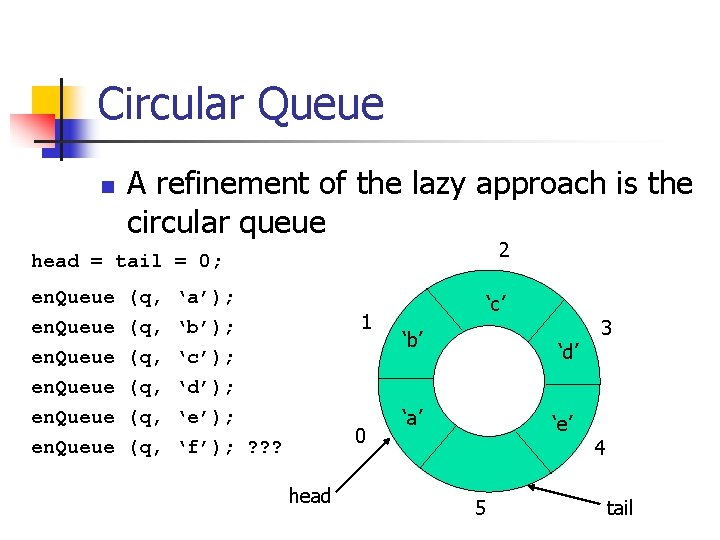
Circular Queue n A refinement of the lazy approach is the circular queue 2 head = tail = 0; en. Queue (q, (q, (q, ‘a’); ‘b’); ‘c’); ‘d’); ‘e’); ‘f’); ? ? ? 1 0 head ‘c’ ‘b’ ‘d’ ‘a’ ‘e’ 5 3 4 tail

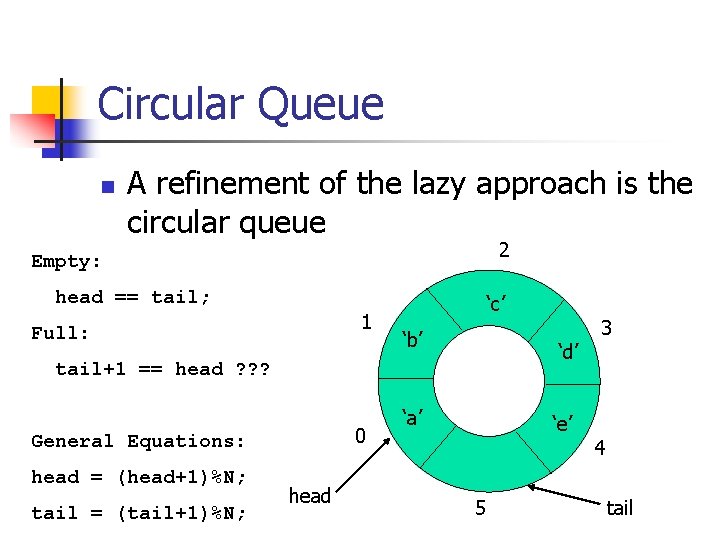
Circular Queue n A refinement of the lazy approach is the circular queue 2 Empty: head == tail; 1 Full: ‘c’ ‘b’ ‘d’ tail+1 == head ? ? ? 0 General Equations: head = (head+1)%N; tail = (tail+1)%N; head ‘a’ ‘e’ 5 3 4 tail

Circular Queue // Cook these together, we can implement the // input buffer using queue: struct Buffer_t { char buf[128]; int head; int tail; }; struct Buffer_t; // Rethink the key pressing, and “getchar ()”?

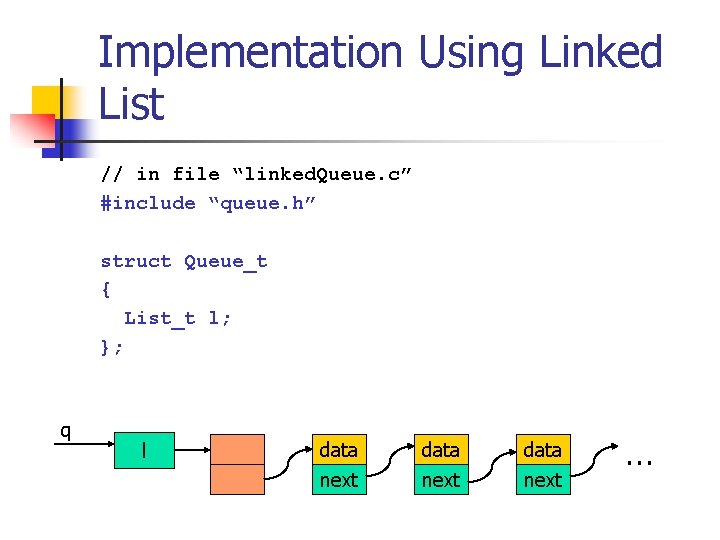
Implementation Using Linked List // in file “linked. Queue. c” #include “queue. h” struct Queue_t { List_t l; }; q l data next …

Operations: “new” Queue_t Queue_new () { Queue q = malloc (sizeof (*q)); q->l = Linked. List_new (); return q; } q l / /

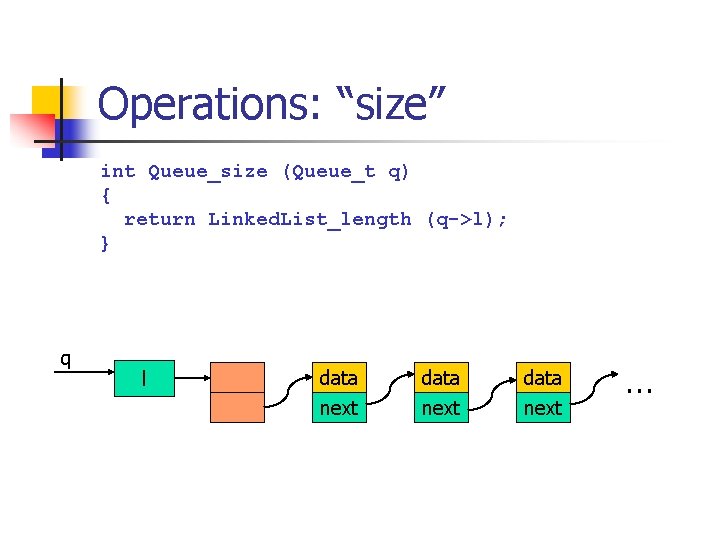
Operations: “size” int Queue_size (Queue_t q) { return Linked. List_length (q->l); } q l data next …

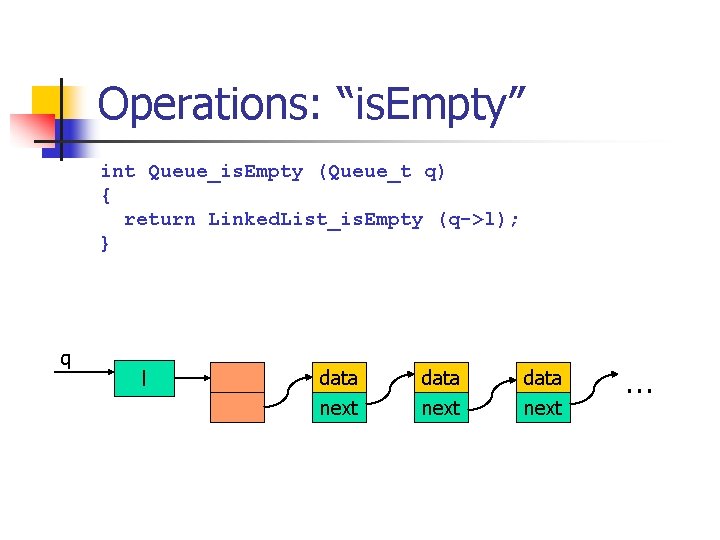
Operations: “is. Empty” int Queue_is. Empty (Queue_t q) { return Linked. List_is. Empty (q->l); } q l data next …

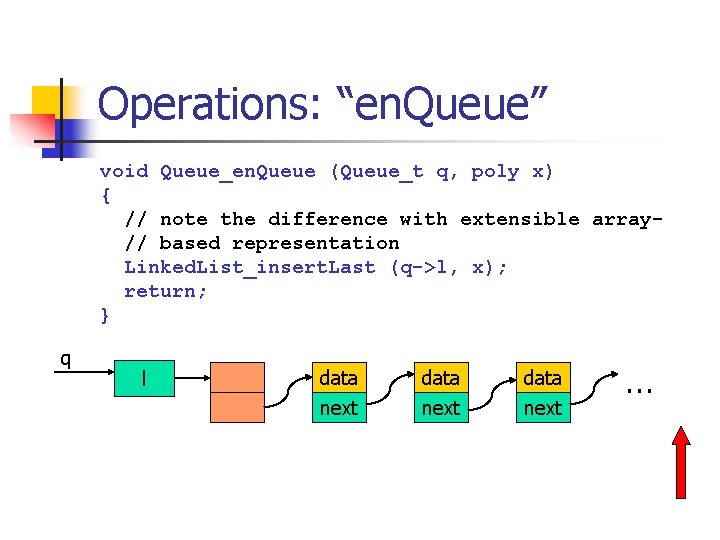
Operations: “en. Queue” void Queue_en. Queue (Queue_t q, poly x) { // note the difference with extensible array// based representation Linked. List_insert. Last (q->l, x); return; } q l data next …

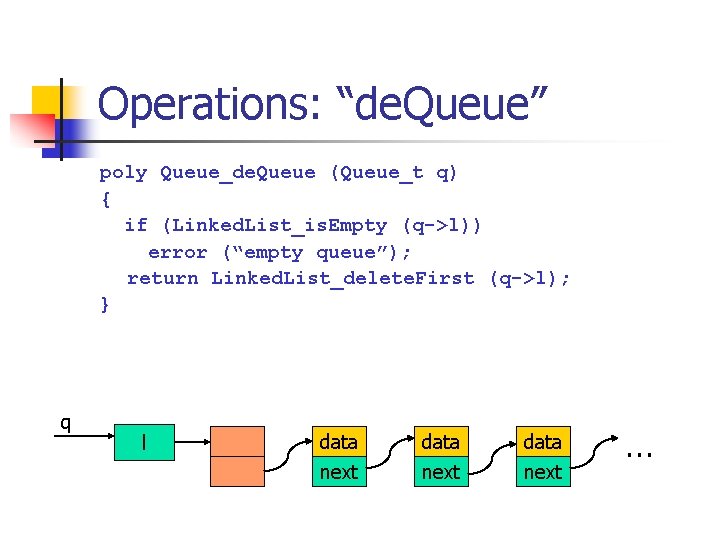
Operations: “de. Queue” poly Queue_de. Queue (Queue_t q) { if (Linked. List_is. Empty (q->l)) error (“empty queue”); return Linked. List_delete. First (q->l); } q l data next …

Analysis n What’s the complexity of these operations? n en. Queue: O(n) n n n search the last element de. Queue: O(1) Improvement: Circular linked list n leave as programming assignment