Query Processing Relational Algebra ayutelkomuniversity ac id Relational

Query Processing: Relational Algebra ayu@telkomuniversity. ac. id

Relational Algebra • Basic operators – Selection ( ), select a subset of rows from relation – Project ( ), deletes unwanted columns from relation – Union ( ), tuples in relation 1 and in relation 2 – set difference ( – ), tuples in relation 1 but not in relation 2 – Cartesian product (x), allows us to combine 2 relations – Rename ( ), renaming the relations – Join ( ) – Aggreagte Function • The operators take one or two relations as inputs and produce a new relation as a result.

Select Operation – Basic Concept • • • Notation: p(r) Used to select a subset of the tuples from a relation that satisfy a selection condition. Defined as: p(r) = {t | t r and p(t)} Where p is a formula in propositional calculus consisting of terms connected by : (and), (or), (not) Each term is one of: <attribute> op <attribute> or <constant> where op is one of: =, , >, . <. Select * from r where p

Select Operation – Example • Relation r country_id country_name region_id 1 US 1 2 Indonesia 3 3 Canada 1 4 Spain 2 5 England 2 • country_name = ‘Indonesia’ (r) country_id country_name region_id 2 Indonesia 3
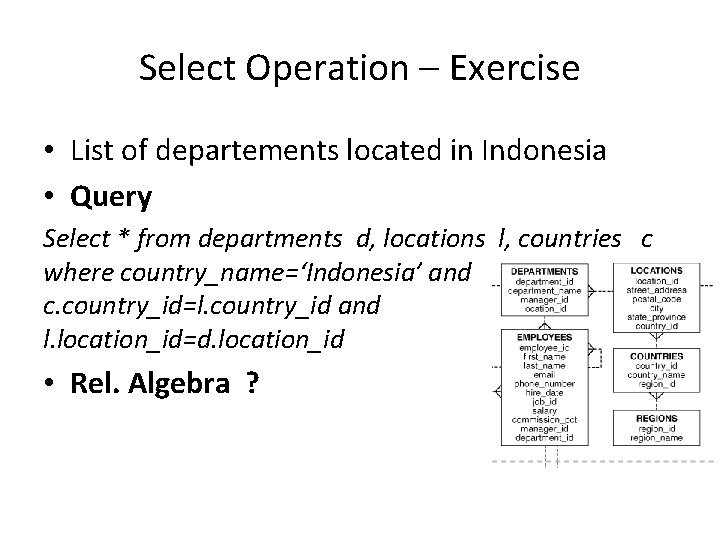
Select Operation – Exercise • List of departements located in Indonesia • Query Select * from departments d, locations l, countries c where country_name=‘Indonesia’ and c. country_id=l. country_id and l. location_id=d. location_id • Rel. Algebra ?

Project Operation – Basic Concept • Notation: where A 1, A 2 are attribute names and r is a relation name. • The result is defined as the relation of k columns obtained by erasing the columns that are not listed • Duplicate rows removed from result, since relations are sets • Example: To eliminate the country_id and region_id attribute of countries country_name (countries)

Project Operation – Example Relation r employee_id first_name last_name email phone_number emp_001 Jose Mourinho mou@blue. com +612345678 emp_002 Brendan Rodgers br@red. com emp_003 David Moyes moyes@red. net +612345680 +612345679 last_name email Mourinho mou@blue. com Rodgers br@red. com Moyes moyes@red. net

Project Operation – Exercise • List of name of employees and department name where they work in • Query Select first_name, last_name, departement_name from employees e, departments d where e. department_id=d. department_id • Rel. Algebra ?

Union Operation – Basic Concept • Notation: r s • Defined as: r s = {t | t r or t s} • For r s to be valid. 1. r, s must have the same arity (same number of attributes) 2. The attribute domains must be compatible (example: 2 nd column of r deals with the same type of values as does the 2 nd column of s) • Example: manager_id (departments) manager_id (employees)

Union Operation – Example • Relation r • r s country_name region_id US Indonesia America Asia Canada America Spain Europe England Europe • Relation s Thailand South Africa Indonesia US Indonesia Europe Asia Africa Asia America Asia Canada America Spain Europe England Europe Italy Europe Thailand country_name region_id Italy country_name region_id South Africa Asia Africa

Type Compatibility • Two Relations are union-compatible if they have the same degree (i. e. , the same number of attributes) and the corresponding attributes are defined on the same domains. • Suppose we have these tables : • developing. Countries (c_id, c_name, region_id) • Countries (country_id, country_name, region_id) – These are union-compatible tables • Union, intersection and set difference require union -compatible tables

Intersection Operation – Basic Concept • The result of this operation, denoted by R ∩ S, is a relation that includes all tuples that appear in both R and S. The two operands must be "type compatible" • Example: Relation r Relation s r ∩ s country_name region_id US America Indonesia Asia Canada America Spain Europe England Europe country_name region_id Indonesia Asia Spain Europe England Europe Italy Europe Thailand Asia South Africa country_name region_id Indonesia Asia Spain Europe England Europe

Set Difference Operation – Basic Concept • Notation r – s • Defined as: r – s = {t | t r and t s} • Set differences must be taken between compatible relations. – r and s must have the same arity – attribute domains of r and s must be compatible

Set Difference Operation – Example Relation r Relation s country_name region_id US America Indonesia Asia Canada America Spain Europe England Europe country_name region_id Indonesia Asia Spain Europe England Europe Italy Europe Thailand Asia South Africa r - s country_name region_id US America Canada America

Cartesian-Product Operation – Basic Concept • Notation r x s • Defined as: r x s = {t q | t r and q s} • Assume that attributes of r(R) and s(S) are disjoint. (That is, R S = ). • If attributes of r(R) and s(S) are not disjoint, then renaming must be used.

Cartesian-Product Operation – Example Relation r r x s country_name region_name Spain Europe England Europe Relation s last_name country_name region_name last_name email Spain Europe Mourinho mou@blue. com Spain Europe Rodgers br@red. com Spain Europe Moyes moyes@red. net England Europe Mourinho mou@blue. com England Europe Rodgers br@red. com England Europe Moyes moyes@red. net email Mourinho mou@blue. com Rodgers br@red. com Moyes moyes@red. net Cartesian Product : combine information from 2 tables, produces every possible combination

Composition of Operations • Can build expressions using multiple operations • Example: country_name, last_name region_name=‘Europe’ (r x s) country_name region_name last_name email Spain Europe Mourinho mou@blue. com Spain Europe Rodgers br@red. com Spain Europe Moyes moyes@red. net England Europe Mourinho mou@blue. com England Europe Rodgers br@red. com England Europe Moyes moyes@red. net Indonesia Asia Mourinho mou@blue. com Indonesia Asia Rodgers br@red. com Indonesia Asia Moyes moyes@red. net • country_name last_name Spain Mourinho Spain Rodgers Spain Moyes England Mourinho England Rodgers England Moyes

Properties • Notice that both union and intersection are commutative operations; that is R ∪ S = S ∪ R, and R ∩ S = S ∩ R • Both union and intersection can be treated as n-ary operations applicable to any number of relations as both are associative operations; that is R ∪ (S ∪ T) = (R ∪ S) ∪ T, and (R ∩ S) ∩ T = R ∩ (S ∩ T) • The minus operation is not commutative; that is, in general R - S ≠ S – R

Rename Operation • Allows us to name, and therefore to refer to, the results of relationalalgebra expressions. • Allows us to refer to a relation by more than one name. • Example: x (E) returns the expression E under the name X • If a relational-algebra expression E has arity n, then returns the result of expression E under the name X, and with the attributes renamed to A 1 , A 2 , …. , An. • It returns a new relation with the same schema and content of the original, just different name (for the relation, attributes or both) • The original relation is unchanged!
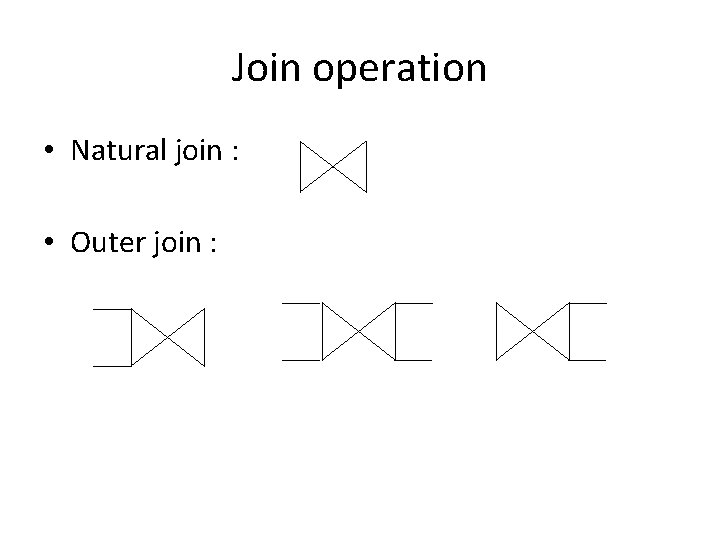
Join operation • Natural join : • Outer join :

Division Operation – Basic Concept • Notation: r s • Suited to queries that include the phrase “for all”. • Let r and s be relations on schemas R and S respectively where – R = (A 1, …, Am , B 1, …, Bn ) – S = (B 1, …, Bn) The result of r s is a relation on schema R – S = (A 1, …, Am) r s = { t | t R-S (r) u s ( tu r ) } Where tu means the concatenation of tuples t and u to produce a single tuple

Division Operation – Example Relation s Relation r country_name last_name email Spain Mourinho mou@blue. com Spain Rodgers br@red. com Indonesia Moyes moyes@red. net Indonesia Mourinho mou@blue. com England Rodgers br@red. com England Moyes moyes@red. net last_name Rodgers email br@red. com country_name Spain England

Aggregate Functions – Basic Concept • Aggregation function takes a collection of values and returns a single value as a result. avg: average value min: minimum value max: maximum value sum: sum of values count: number of values • Aggregate operation in relational algebra – E is any relational-algebra expression – G 1, G 2 …, Gn is a list of attributes on which to group (can be empty) – Each Fi is an aggregate function – Each Ai is an attribute name
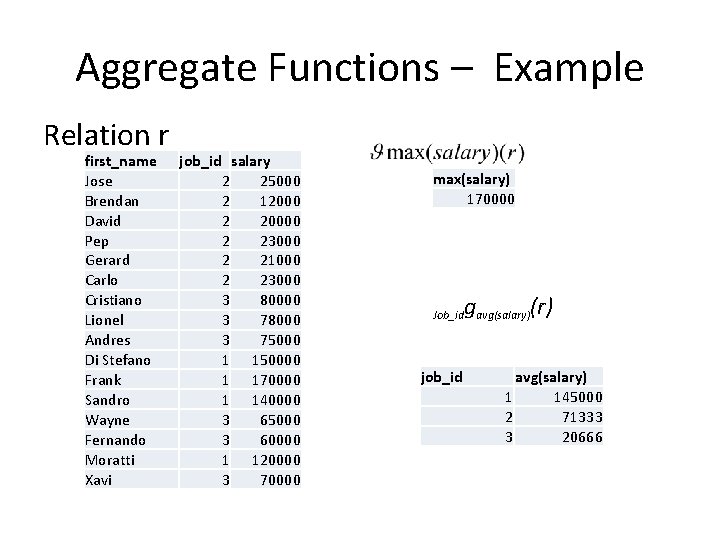
Aggregate Functions – Example Relation r first_name Jose Brendan David Pep Gerard Carlo Cristiano Lionel Andres Di Stefano Frank Sandro Wayne Fernando Moratti Xavi job_id salary 2 25000 2 12000 2 20000 2 23000 2 21000 2 23000 3 80000 3 78000 3 75000 1 150000 1 170000 1 140000 3 65000 3 60000 1 120000 3 70000 max(salary) 170000 Job_id job_id gavg(salary)(r) avg(salary) 1 145000 2 71333 3 20666

• Diketahui skema basis data sbb: employee (person-name, street, city) works (person-name, company-name, salary) company (company-name, city) manages (person-name, manager-name) a. Cari nama employee yang bekerja pada Bank Niaga. b. Cari nama dan kota tempat tinggal semua employee yang bekerja di Bank Niaga. c. Cari nama, alamat dan kota tempat tinggal semua employee yang bekerja di Bank Niaga dan berpenghasilan lebih dari Rp 2. 000. d. Cari nama semua employee yang tinggal di kota yang sama dengan perusahaan dimana mereka bekerja. e. Cari nama semua employee yang tinggal di kota dan jalan yang sama dengan manager mereka. f. Cari nama semua employee yang tidak bekerja di Bank Niaga. h. Asumsikan perusahaan berlokasi di beberapa kota. Cari semua perusahaan yang berlokasi di setiap kota dimana Small Bank Corporation berada.
- Slides: 25