Query Processing Exercise Session 2 1 Question 1

Query Processing Exercise Session 2 1

Question 1 • A segment of R and a segment of S have to be joined on A • All the records in these two segments have the same value for A • So, it is actually a Cartesian product • What is the best method? • What is the I/O cost? 2

Sort-Merge Join 3

Division into Lists • Divide R and S into equal-length lists so that the total number of lists is n = √(B(R) + B(S)) • Size of each list is ? • Number of list of R M 1 = ? • Number of list of S M 2 = ? • What is the I/O cost of dividing into lists (without the sorting which is the next step)? 4

Sorting the Lists • For each list, do the following: – Read the whole list into main memory – Sort it in main memory – Write the sorted list back to disk • What is the total cost for R and S ? • What is the needed buffer size? 5

Scanning the Sorted Lists • We read the lists simultaneously in sorted order • How many blocks in the buffer pool are needed for each list? – One for each list, namely, a total of M 1 + M 2 – Plus one more for the output • How to advance the pointers? – See the animation in the lecture’s slides 6

Joining • The scanning has discovered a segment of R and a segment of S that have to be joined • So, we join the two segments, which means that now we read all the records that have to be joined • How many buffer blocks are needed to do it in just one pass? • After joining the two segments, we continue the scan 7

Block Nested-Loop Join 8

Problems to Solve • Prove the optimality of the buffer allocation in nested-loop join of two relations • How would you join three relations using nested loops? – What is the buffer allocation? • How would you do it without writing temporary results to the disk? • Give a sufficient condition for the I/O cost to be the best possible 9

Solutions 10

Optimal Buffer Allocation • Question: Prove the optimality of the buffer allocation in nested-loop join of two relations • Answer: The I/O cost is �B(R)/M� B(S) + B(R) – It depends on the number of buffer blocks allocated to R – the more the better – It does not depend on the number of blocks allocated to S – Hence, we maximize the number of blocks for R, and allocate a single buffer block to S 11

Three Variants of Block Nested Loop for Joining 3 Relations R ⋈S ⋈T 12

Writing the Intermediate Result to Disk • One way of computing R ⋈S ⋈T is by joining R and S, writing the result to the disk and then joining that result with T M 1 blocks for the • Let W = R ⋈S relation in the outer • The I/O cost of the first join is loop, one for the �B(R)/M B(S) + B(R) 1� other relation, and • The I/O cost of the second join is one for the output �B(W)/M 1� B(T) + B(W) – But this is the cost when W is already on the disk – So, we should add the cost B(W) of writing W (recall that we only ignore the cost of writing the final result, but not of writing intermediate ones) • Thus, the total I/O cost is �B(R)/M B(S) + B(R) + �B(W)/M 1� B(T) + 2 B(W) 1� 13

Comments on the Previous Slide • To calculate the I/O cost, we should be able to estimate the size of W • In each of the two joins, which relation should be in the outer loop to get the best I/O cost? – What is the I/O cost if W is in the inner loop? • Which join should be done first? R ⋈S, S ⋈T or R ⋈T ? – The answer depends also on the size of the result of the first join, and can only be determined by calculating the full I/O cost of each alternative 14

First Method of Pipelining: Three Nested Loops In pipelining, no intermediate result is written to disk 15

Pipelined Nested-Loop Join • The next slide generalizes nested-loop join to 3 relations • This computation of R ⋈S ⋈T does not write any intermediate result to the disk – It pipelines the result of one join into the computation of the other join – The outermost loop scans R just once – In each iteration of the outermost loop, the two inner loops compute S ⋈T • The I/O cost is �B(R)/M [�B(S)/N B(T) + B(S) ] + B(R) 2� 2� 16

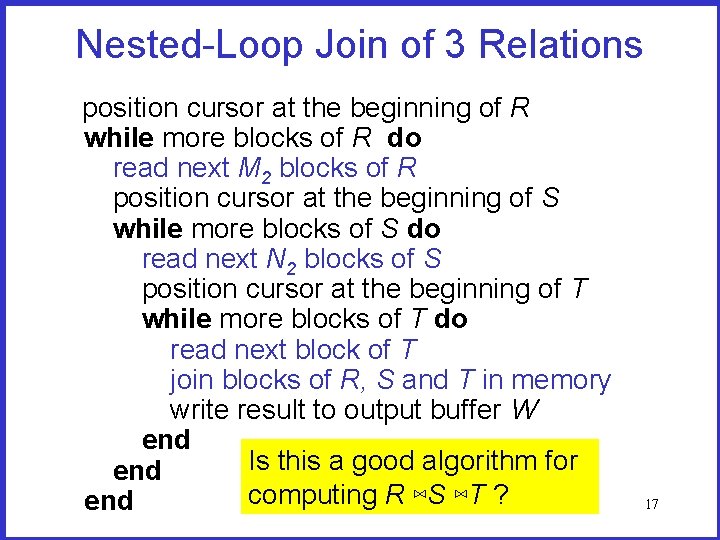
Nested-Loop Join of 3 Relations position cursor at the beginning of R while more blocks of R do read next M 2 blocks of R position cursor at the beginning of S while more blocks of S do read next N 2 blocks of S position cursor at the beginning of T while more blocks of T do read next block of T join blocks of R, S and T in memory write result to output buffer W end Is this a good algorithm for end computing R ⋈S ⋈T ? end 17

Comments on Slides 16 & 17 • Is it optimal to have the smallest relation in the outermost loop and the biggest relation in the innermost loop? • One block for T is optimal (why? ) • So, the remaining buffer blocks should be divided between R and S, that is, we should find M 2 and N 2 that minimize the I/O cost, subject to the constraint that M 2 +N 2 is a constant (equals to the total buffer size minus one block for T and another for the output) • How does this compare with the I/O cost and buffer allocation in Slide 13? 18

Second Method: Pipelining to Outer Loop 19

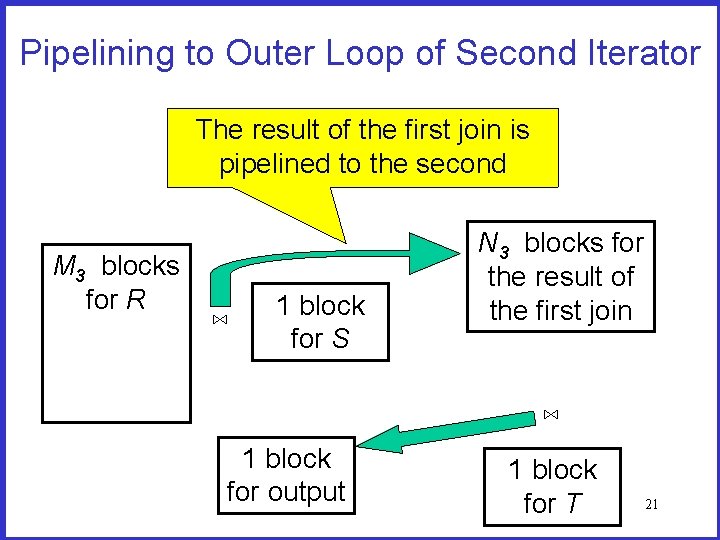
Two Iterators: Each is a Double Loop • The algorithm of the previous method computes the join of S and T many times • An alternative is to compute each join just once • We do it by using two iterators – Each iterator computes one join by using two nested loops – The first iterator pipelines its result to the outer loop of the second iterator (see figure on next slide) – When the first iterator fills the N 3 blocks allocated to its result, it waits until the second iterator computes the join of these N 3 blocks and the whole of T • The first join is computed only once! 20

Pipelining to Outer Loop of Second Iterator The result of the first join is pipelined to the second M 3 blocks for R ⋈ 1 block for S N 3 blocks for the result of the first join ⋈ 1 block for output 1 block for T 21

I/O Cost of Pipelining to Outer Loop • Let W = R ⋈S • The I/O cost of the first join is �B(R)/M B(S) + B(R) 3� • The I/O cost of the second join is only �B(W)/N 3� B(T) – Because we do not to read W from the disk • Thus, the total I/O cost is �B(R)/M B(S) + B(R) + �B(W)/N 3� B(T) 3� 22

Comments on the Previous Slide • Why is it optimal to allocate just one block to each of S and T ? • What is the total number of buffer blocks? • How should we determine the optimal values of M 3 and N 3 ? • Which join should be computed first? 23

I/O Cost & Constraint on Mi and Ni shown for each of the three methods, but only when the join order is R ⋈S ⋈T • Slide 13 (optimal buffer allocation is trivial): �B(R)/M B(S) + B(R) + �B(W)/M 1� B(T) + 2 B(W) 1 )� M 1 + 2 = # of available blocks • Slide 16: �B(R)/M [�B(S)/N B(T) + B(S) ] + B(R) 2� 2� M 2 + N 2 + 2 = # of available blocks • Slide 22: �B(R)/M B(S) + B(R) + �B(W)/N 3� B(T) 3� M 3 + N 3 + 3 = # of available blocks In Slides 13 and 22, the I/O cost depends on the size of the intermediate result W 24

Comparing I/O Costs in Slides 13, 16 & 22 • Is one of these three I/O costs always better than the other two? • Is one of these three I/O costs always worse than the other two? • Compare the I/O costs of the two ways of pipelining (Slides 16 & 22) – Is one always better than the other? – Hint: Is it always true that B(W) B(R) B(S) ? The answer is no – can you see why? • How can we determine the optimal buffer allocation (i. e. , Mi and Ni) in each of Slides 16 and 22? • How can we determine the optimal join order in each of Slides 13, 16 and 22? 25

Summary • We presented three variants of block nestedloops for joining three relations • In each variant, finding the best join order (out of the possible three) is not trivial • For two variants, finding the optimal buffer allocation is a non-trivial optimization problem under a constraint • The best variant (and its optimal join order and buffer allocation) depends on the sizes of the relations, the sizes of the intermediate results and the total number of available buffer blocks 26

More Observations • The best possible I/O cost (what is it? ) is achieved when we have enough memory for the smallest two relations, plus one block for the third relation and another block for the output • What is the cost in Slide 22 when N 3 blocks suffice for storing the whole result of the first join? • How to modify the method and cost of Slide 22 when N 3 blocks are sufficient for storing all of T ? • What is the minimal number of buffer blocks needed to join three relations (regardless of the I/O cost)? 27