Query languages equivalence containment conjunctive queries CQs More

Query languages, equivalence & containment Ø conjunctive queries – CQ’s ØMore expressive languages 2005 conjunctive 1

Conjunctive queries The users of an integrated system can use SQL (or XQuery, …) Q: What language should one use for relating sources to the global schema? A: conjunctive queries (CQ’s), or extensions of them CQ’s are equivalent to a subset of SQL Their advantages: • Simple syntax, easy to analyze • Easily extended to more powerful languages 2005 conjunctive 2

A simple subset of SQL: SELECT t 1. A 1, …, tk. Ak FROM R 1 as t 1, … Rk as tk, … Rn as tn WHERE C Here, C is a conjunction of equality conditions of the form Ti. A = tj. B or ti. A = c Alternative syntax (CQ): A rule (here, p is a new predicate name) body head p(t 1. A 1, … tk. Ak) : - R 1(t 1), Rk(tk), …Rn(tn), C and These queries can be expressed by select-project-join in relational algebra (using only equality conditions) 2005 conjunctive 3

Example: movies(Title, Director, Actor) Directory(Theatre, Title, Hour) Location(Theatre, Address, Phone) Q: Who is the director of the movie ‘The birds’? SQL: SELECT m. Director FROM movies as m WHERE Title = ‘The birds’ CQ: ans(m. Director) : - movies(m), m. Title = ‘The birds’ 2005 conjunctive 4

Often we prefer individual variables over tuple variables ans(D) : - movies(T, D, A), T = ‘The birds’ Now, the equality can be pushed inside, giving the simpler form ans(D) : - movies(‘The birds’, D, A) Q: show directors of movies shown in Plaza at 19: 00 q(D) : - movies(T, D, A), directory(‘Plaza’, T, 19: 30) 2005 conjunctive 5

Some terminology: • A predicate – name of a relation • Extensional predicate – name of a db relation • Intentional predicate – name of a new relation • Atom – R(s 1, …, sn), where each si is is a variable or constant • Ground atom – contains only constants • CQ: a rule of the form head body , where – head – an atom of intentional predicate (any pred. name acceptable) – body – a conjunction of extensional (db) atoms – Every variable that occurs in the head also occurs in the body (safety) Variables that occur only in body are existential (see examples prev. page) 2005 conjunctive 6

What is the semantics of a CQ? – the definition of answer: • Valuation (variable assignment) – a mapping v of variables to constants • Is naturally extended to atoms and rules • Transforms each body atom R(t 1, …tn) to a ground atom R(v(t 1), …v(tn)) If, for a given rule, for each body atom , v(R(t 1, …tn)) is in the database, then the image of v(head(Q)) in the answer The above is the standard notion of a query answer A valuation is sometimes called a homomorphism from the query body to the db – why? 2005 conjunctive 7

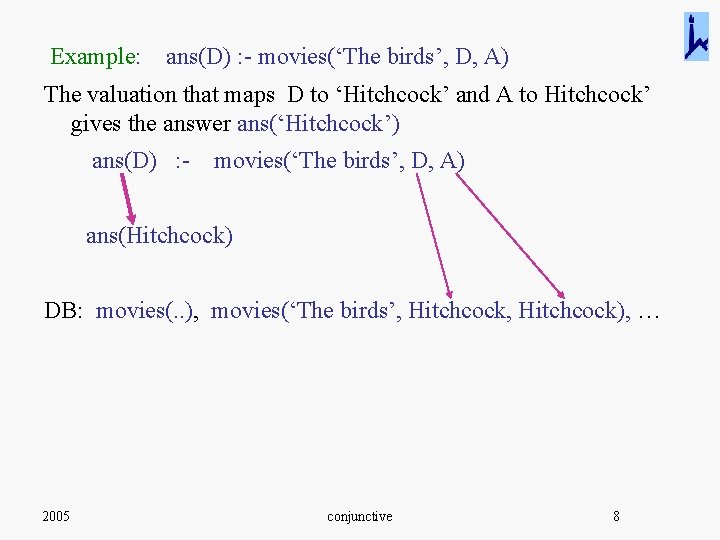
Example: ans(D) : - movies(‘The birds’, D, A) The valuation that maps D to ‘Hitchcock’ and A to Hitchcock’ gives the answer ans(‘Hitchcock’) ans(D) : - movies(‘The birds’, D, A) ans(Hitchcock) DB: movies(. . ), movies(‘The birds’, Hitchcock), … 2005 conjunctive 8

Consequences: • Names of variables used in a CQ are irrelevant; they can be replaced w/o changing the semantics • The variables that occur only in the body are existentially quantified for a given assignment to the head variables, we need some assignment to the existential variables to obtain an answer Comment: Computing the answer using the semantics is typically expensive In practice, query is compiled to relational algebra, then to query plan, using indices, etc. This is known technology mostly ignored in this course 2005 conjunctive 9

Variations on the form of CQ’s – summary: 1) Distinct individual variables, equalities on the side q(D) : - movies(T, D, A), directory(Th, T 1, H), Th=‘Plaza’, T = T 1, H= 19: 30 2) All equalities pushed inside q(D) : - movies(T, D, A), directory(‘Plaza’, T, 19: 30) 3) Using tuple variables, with equalities on the side q(m. Director) : - movies(m), directory(d), m. Title = d. Title, d. Hour = 19: 30 • All equivalent, we often use 2 • When inequalities are added, they must occur on the side 2005 conjunctive 10

ØMore expressive languages I. Use inequalities in the body or comparison predicates comparisons are called built-in predicates The domain of variables is then one of • A dense totally ordered domain (e. g. , the reals) • A discrete totally ordered domain (integers, strings) The additional constraints occur on the side The semantics: a valuation that • is a homomorphism on the atoms in the query body • That satisfies the additional constraints 2005 conjunctive 11

II. Several rules with the same head predicate Example: assume a graph is represented by edge(from, to) small-d(x, y) : - edge(x, y) small-d(x, y) : - edge(x, z), edge(z, y) customary notation: same head variables, (& different existentials) The semantics: or, that is union A tuple is in the answer iff it is obtained by one of the rules 2005 conjunctive 12

III. A set of rules that use one or more intentional (new) predicates One of these is singled out as the answer predicate The language of such program/queries is called Datalog Example: the transitive closure of a directed graph connected(x, y) : - edge(x, y) connected(x, y) : - connected(x, z), edge(z, y) This is a recursive program 2005 conjunctive 13

Example: assume the db contains two relations mother(person, child), father(person, child), Then the grandparent relation can be defined by parent(x, y) : - mother(x, y) parent(x, y) : - father(x, y) g-parent(x, y) : - parent(x, z), parent(z, y) A non-recursive program To obtain the grandparent of Gustav, we can add ans(x) : - g-parent(x, ‘Gustav’) 2005 conjunctive 14

When is a datalog program recursive? A predicate p depends on a predicate q iff p occurs in the head of a rule and q occurs in its body A program is recursive iff the transitive closure of ‘depends on’ is cyclic connected(x, y) : - edge(x, y) connected(x, y) : - connected(x, z), edge(z, y) connected 2005 conjunctive 15

The semantics of general datalog programs : A proof tree: • Nodes are ground atoms • For each internal node n, with children n 1, . . , nk, there is a rule r: p(. . ) : - r 1(. . ), … rk(. . ) , C and a valuation v such that • n = v(p(. . )) • ni = v(ri(. . )) • v(C ) is satisfied • For each leaf, the node is a db fact A ground atom (fact) is in the semantics of a program iff it has a proof tree 2005 conjunctive 16

Example : r 1: u-connected(x, y) : - edge(x, y), x<y r 2: u-connected(x, y) : - u-connected(x, z), edge(z, y) Assume the db contains the facts edge(3, 4), edge(3, 2), edge(4, 6), edge(6, 5) , edge(2, 7) a proof tree: u-connected(3, 6) u-connected(3, 5) r 2 u-connected(3, 4) r 1 edge(3, 4) 2005 edge(4, 6) conjunctive edge(6, 5) 17

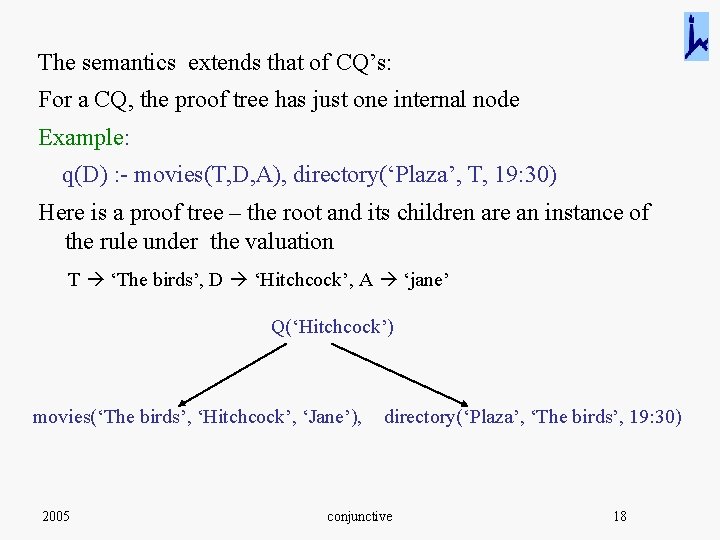
The semantics extends that of CQ’s: For a CQ, the proof tree has just one internal node Example: q(D) : - movies(T, D, A), directory(‘Plaza’, T, 19: 30) Here is a proof tree – the root and its children are an instance of the rule under the valuation T ‘The birds’, D ‘Hitchcock’, A ‘jane’ Q(‘Hitchcock’) movies(‘The birds’, ‘Hitchcock’, ‘Jane’), 2005 directory(‘Plaza’, ‘The birds’, 19: 30) conjunctive 18

An evaluation strategy for recursive programs: bottom-up naïve evaluation Start with the given db, and with all other relations empty Do until no more changes: apply all rules (to obtain new facts for all intentional predicates) Example: (The u-connected example) (only the new facts are shown) 1 st round : (only r 1 derives facts) u-connected(3, 4), u-connected(4, 6), u-connected(2, 7) 2 nd round : (only r 2 derives new facts, r 1 derives known facts) u-connected(3, 6), u-connected(4, 5) 3 rd round: (same) u-connected(3, 5) 2005 conjunctive 19

Last extension: Allow negation in rule bodies, on intentional predicates Here, care is needed, semantics can be undefined r(x) ; - not s(x) : - not r(x) A reasonable restriction: Assume rule sets R 1, …, Rk, such that in Ri negation is applied only to rules of Ri-1 Datalog with stratified negation Each Ri is viewed as a program module The extensions of predicates are computed in order: R 1, R 2, …, Rk 2005 conjunctive 20