Quelques points de repre concernant lenseignement de la

Quelques points de repère concernant l’enseignement de la technique posée de la division à l’école primaire I Rappels destinés aux enseignants II Technique posée de la division euclidienne de deux entiers III Une proposition de progression pour enseigner la technique de la division euclidienne IV Division décimale de deux entiers (au programme du CM 1) V Division d’un décimal par un entier (au programme du CM 2) D. Pernoux http: //dpernoux. net

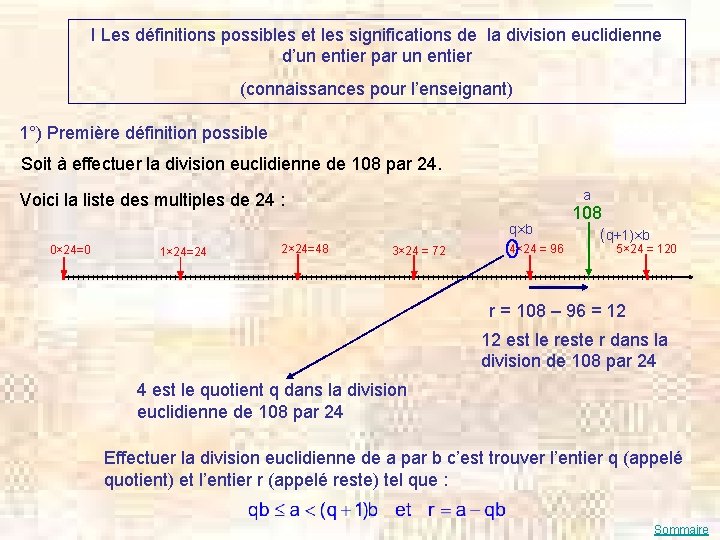
I Les définitions possibles et les significations de la division euclidienne d’un entier par un entier (connaissances pour l’enseignant) 1°) Première définition possible Soit à effectuer la division euclidienne de 108 par 24. a Voici la liste des multiples de 24 : q×b 0× 24=0 1× 24=24 2× 24=48 3× 24 = 72 4× 24 = 96 108 (q+1)×b 5× 24 = 120 r = 108 – 96 = 12 12 est le reste r dans la division de 108 par 24 4 est le quotient q dans la division euclidienne de 108 par 24 Effectuer la division euclidienne de a par b c’est trouver l’entier q (appelé quotient) et l’entier r (appelé reste) tel que : Sommaire

2°) Deuxième définition possible Soit à effectuer la division euclidienne de 108 par 24. On peut écrire de plusieurs manières 108 sous la forme 108 = …× 24 + … 108 = 0 × 24 + 108 = 1 × 24 + 84 108 = 2 × 24 + 60 108 = 3 × 24 + 36 Ce nombre est plus petit que 24 108 = 4 × 24 + 12 a =q× b + r 4 est le quotient q 12 est le reste r dans la division de 108 par 24 euclidienne de 108 par 24 Effectuer la division euclidienne de a par b c’est trouver l’entier q (appelé quotient) et l’entier r (appelé reste) tel que : Sommaire

3°) Les deux significations de la division a) La division peut intervenir dans des situations de partage, de distribution, … situations où on est amené à cher « la valeur d’une part » ( « Combien dans chaque paquet ? » ). On parle alors de division-partition. On dispose de 45 bonbons à partager équitablement entre 6 enfants ? Combien chaque enfant aura-t-il de bonbons ? ? ? ? Division-partition 6 « paquets » . « Combien dans chaque paquet ? » b) La division peut intervenir dans des situations de regroupement, …, situations où on est amené à cher « le nombre de parts » ( « Combien de paquets ? » ). On parle alors de division-quotition. On dispose de 45 bonbons. On désire fabriquer des paquets de 6 bonbons. Combien peut-on fabriquer de paquets ? 6 6 6 …? Division-quotition Des « paquets » de 6. « Combien de paquets » Sommaire

II Aide-mémoire concernant la technique posée de la division euclidienne Sommaire

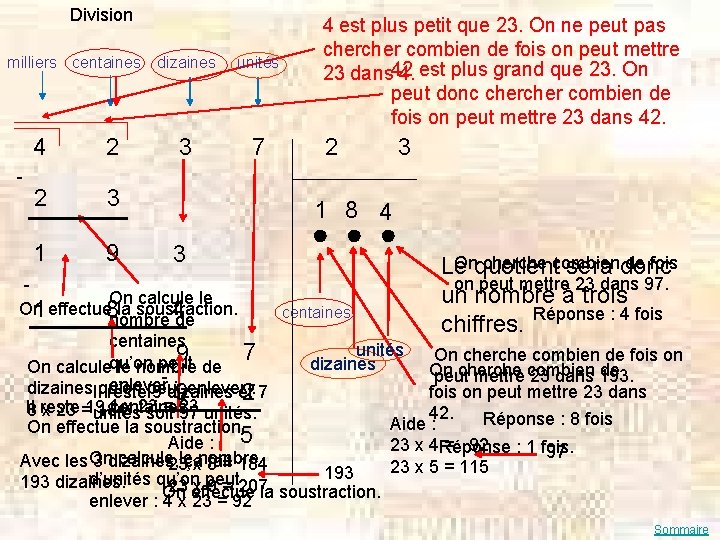
Division milliers centaines - 4 2 2 3 1 9 dizaines unités 3 7 4 est plus petit que 23. On ne peut pas cher combien de fois on peut mettre 23 dans 42 4. est plus grand que 23. On peut donc cher combien de fois on peut mettre 23 dans 42. 2 3 1 8 4 3 Onquotient cherche combien de fois Le sera donc on peut mettre 23 dans 97. un nombre à trois chiffres. Réponse : 4 fois On calcule le On la soustraction. 1 effectue 8 nombre 4 de centaines unités 7 9 On cherche combien de fois on qu’on peut dizaines On calcule le nombre de On cherche de peut mettre combien 23 dans 193. -: enlever dizaines. Ilqu’on enleveret : 7 restepeut 9 dizaines fois on peut mettre 23 dans 9 2 1 x 23 = 23. Il 8 reste centaines x 23 =19 184 unités soit 97 unités. 42. Réponse : 8 fois Aide : On effectue la soustraction. Aide : 5 23 x 4 Réponse = 92 : 1 fois. 97 On calcule le nombre Avec les 3 dizaines, ça fait 23 x 8 = 184 23 x 5 = 115 193 d’unités qu’on peut 193 dizaines. 23 effectue x 9 = 207 la soustraction. On enlever : 4 x 23 = 92 Sommaire

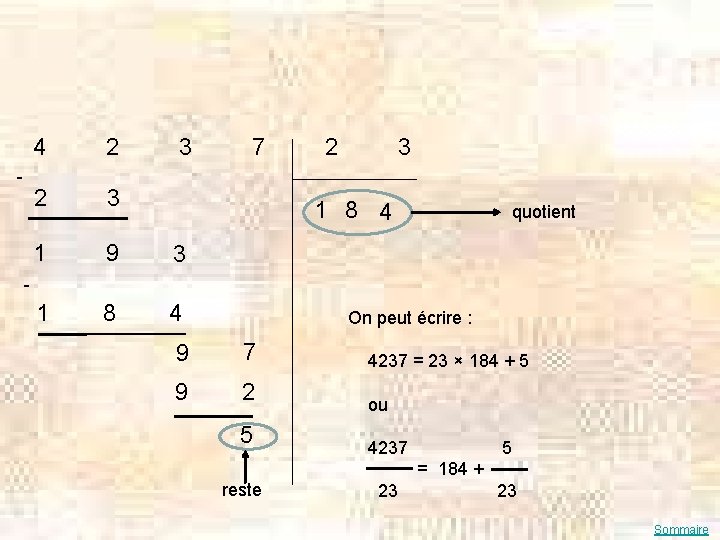
- 4 2 3 1 9 3 1 8 4 7 2 3 1 8 4 quotient On peut écrire : 9 7 4237 = 23 × 184 + 5 9 2 ou 5 4237 5 = 184 + reste 23 23 Sommaire

III Proposition de progression concernant l’apprentissage de la technique de la division euclidienne (le découpage en séances n’est donné qu’à titre indicatif et devra, bien sûr, être adapté au niveau de la classe) Remarque préalable : dans cette progression, la technique est construite de façon progressive en s’appuyant sur une situation-problème initiale et sur les procédures personnelles mises en œuvre par les élèves. On peut bien évidemment faire un autre choix et opter pour une présentation plus directe et plus explicite de la technique. Sommaire

1°) Savoirs et savoir-faire utiles : - savoir faire la différence entre partages équitables et partages non équitables - connaître les techniques de l’addition, de la soustraction et de la multiplication et les tables de multiplication - savoir ce qu’est un multiple et savoir écrire la table des multiples d’un nombre donné (exemple : table des multiples de 16) 2°) Problèmes précédant le travail sur la technique posée traditionnelle (1 séance) - On peut commencer par une situation de regroupement ( « Combien de paquets ? » ) avec un quotient à un chiffre qui permettra de faire un travail sur les multiples sans aborder encore la technique posée traditionnelle. Exemple : 171 bonbons - des paquets de 25 bonbons - combien de paquets ? - On peut continuer par une situation de partage ( « Combien dans chaque paquet ? » ) avec un quotient à un chiffre qui permettra, elle aussi, de faire un travail sur les multiples toujours sans aborder la technique traditionnelle. Exemple : 213 bonbons - 25 enfants – combien de bonbons chacun ? Sommaire

- Problème que les élèves sont amenés à résoudre en utilisant des procédures personnelles Exemple : un géant qui fait des pas de 15 km part de son premier château pour aller vers son deuxième château distant de 3530 km. Combien de pas le géant doit-il effectuer pour atteindre ce deuxième château? La mise en commun permet de faire apparaître les différentes procédures utilisées par les élèves (procédure additive, procédure multiplicative, procédure soustractive, mixage de ces différentes procédures, …) On peut garder sous la forme d’affiches des traces des procédures utilisées de façon à pouvoir s’y référer lors des séances suivantes. On peut écrire à la fin : 3530 = (235 × 15) + 5 Remarque : Il semble préférable, au niveau mathématique d'avoir dès le départ une division avec reste pour ne pas donner une fausse image de la notion de division …et les élèves ne manquent en général pas d'imagination quand il s’agit de savoir si le géant arrivera à atteindre le château : le géant enclenche le frein, le géant se met à ramper. . . ; -) 3°) Elaboration progressive de la technique posée traditionnelle (2 ème séance) Remarque : on peut d’abord faire construire la table des multiples de 15 et demander d’utiliser cette table pour effectuer des calculs du type 5 × 15, 5000 × 15, … Elaborer progressivement la technique posée traditionnelle c’est s’intéresser parmi les différentes procédures utilisées pour résoudre le problème du géant, à la procédure soustractive qu’on va améliorer pour le rendre de plus en plus efficace. Sommaire

On pourra, par exemple, arriver à une présentation de ce type : 3 5 3 0 1 5 0 0 1 5 1 0 0 2 0 3 0 1 5 0 0 1 0 0 5 3 0 1 5 0 1 0 Le géant fait 3 8 0 235 pas 1 5 0 1 0 2 3 0 Il lui reste encore 5 km à parcourir 1 5 0 1 0 8 0 7 5 5 5 Sommaire

4°) Elaboration progressive de la technique posée traditionnelle (suite) (3ème et 4ème séances mais qui ne suivent pas nécessairement immédiatement la deuxième séance) Nouveau problème (problème avec une division-partition alors que le problème du géant était un problème de division-quotition) 24 flibustiers veulent se partager équitablement 3750 pièces d’or. Combien auront-ils chacun ? [Là encore, il y a un reste … (à ajouter à la part du capitaine, à enterrer en prévision de jours plus difficiles, … ? ; -) ] On pourra reprendre une présentation des calculs analogues à celle vue au paragraphe précédent puis l’améliorer pour arriver à : 3 7 5 0 2 4 1 × 24 = 24 2 × 24 = 48 3 × 24 = 72 4 × 24 = 96 5 × 24 = 120 6 × 24 = 144 7 × 24 = 168 8 × 24 = 192 9 × 24 = 216 On peut écrire : 3750 = (156 × 24) + 6 2 4 0 0 1 3 5 0 1 2 0 0 5 0 1 4 4 6 6 On utilise la table des multiples de 24 pour donner le maximum de paquets de 100 pièces, puis le maximum de paquets de 10 pièces puis le maximum de pièces. Sommaire

5°) Elaboration progressive de la technique posée traditionnelle (suite) (5ème séance mais qui ne suit pas nécessairement immédiatement les précédentes et qui peut ne concerner que le CM 2) - Travail sur le nombre de chiffres du quotient : Sans effectuer les divisions, trouver le nombre de chiffres du quotient (indiquer le nombre de chiffres du quotient en mettant – ou – – – à la place du quotient) et expliquer comment vous faites pour le trouver. 825 15 1480 17 53 9 3 7 5 0 - Technique posée traditionnelle : 2 4 0 0 2 4 _1 _5 6 _ 1 3 5 0 1 2 0 0 1 5 0 1 4 4 6 Sommaire

- Remarque : Il peut être éventuellement envisageable de travailler avec certains élèves la « technique dépouillée » mais il ne semble pas souhaitable d’exiger que tous les élèves sachent utiliser cette technique. 3 7 5 0 1 3 5 1 5 0 2 4 1 5 6 6 Merci à Jean-Georges Schiele pour ses apports. Sommaire

IV Division décimale de deux entiers (au programme du CM 1) - 4 2 2 3 1 9 3 7 , 0 0 1 8 3 1 4 , 2 Quotient décimal approché au centième : 184, 21 - 1 2 4 On peut écrire : - 9 7 4237 = 23 × 184, 21 + 0, 17 9 2 ou 4237 0 5 -5 c’est 50 4 6 dixièmes 0, 17 = 184, 21 + 23 4 0 1 7 4 dixièmes 2 3 c’est 40 centièmes 23 Sommaire

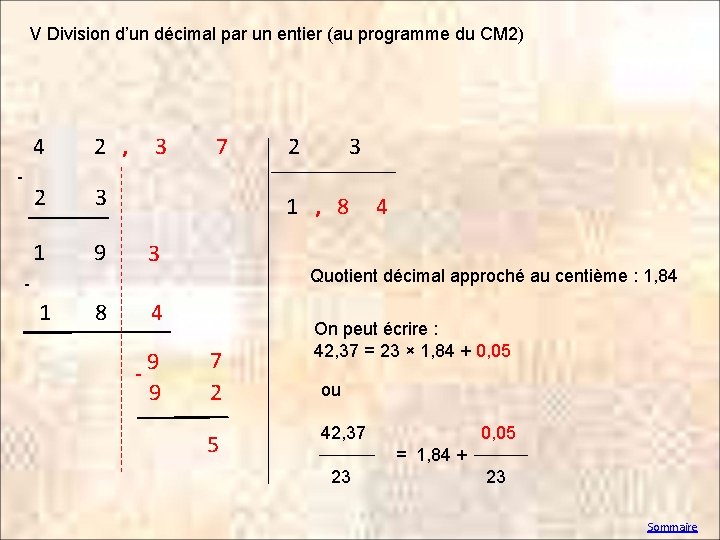
V Division d’un décimal par un entier (au programme du CM 2) - 4 2 , 3 2 3 1 9 3 1 8 4 7 2 3 1 , 8 Quotient décimal approché au centième : 1, 84 - - 9 9 4 7 2 5 On peut écrire : 42, 37 = 23 × 1, 84 + 0, 05 ou 42, 37 0, 05 = 1, 84 + 23 23 Sommaire