Quartz Crystal Resonators and Oscillators John R Vig

Quartz Crystal Resonators and Oscillators John R. Vig US Army Communications-Electronics Research, Development & Engineering Center Fort Monmouth, NJ, USA J. Vig@IEEE. org

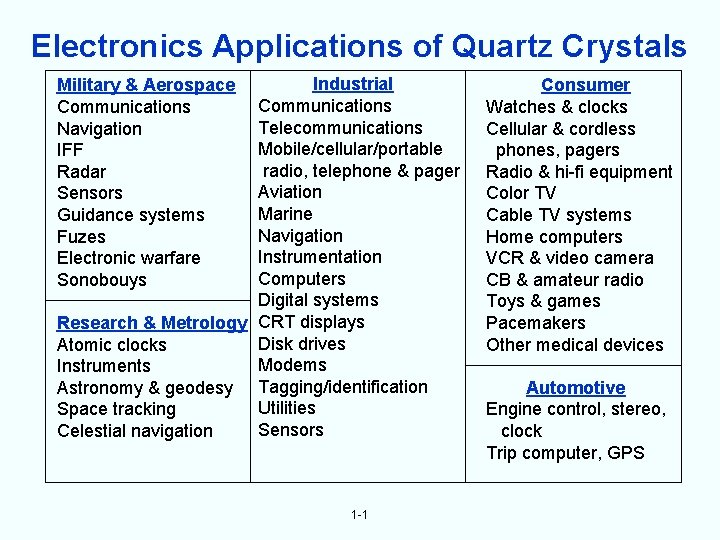
Electronics Applications of Quartz Crystals Industrial Communications Telecommunications Mobile/cellular/portable radio, telephone & pager Aviation Marine Navigation Instrumentation Computers Digital systems Research & Metrology CRT displays Disk drives Atomic clocks Modems Instruments Astronomy & geodesy Tagging/identification Utilities Space tracking Sensors Celestial navigation Military & Aerospace Communications Navigation IFF Radar Sensors Guidance systems Fuzes Electronic warfare Sonobouys Consumer Watches & clocks Cellular & cordless phones, pagers Radio & hi-fi equipment Color TV Cable TV systems Home computers VCR & video camera CB & amateur radio Toys & games Pacemakers Other medical devices Automotive Engine control, stereo, clock Trip computer, GPS 1 -1

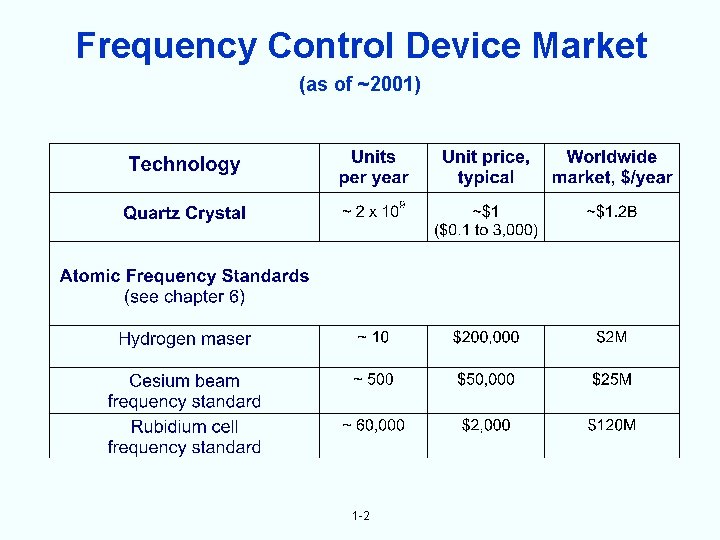
Frequency Control Device Market (as of ~2001) 1 -2

Impacts of Oscillator Technology Improvements Higher jamming resistance & improved ability to hide signals Improved ability to deny use of systems to unauthorized users Longer autonomy period (radio silence interval) Fast signal acquisition (net entry) Lower power for reduced battery consumption Improved spectrum utilization Improved surveillance capability (e. g. , slow-moving target detection, bistatic radar) Improved missile guidance (e. g. , on-board radar vs. ground radar) Improved identification-friend-or-foe (IFF) capability Improved electronic warfare capability (e. g. , emitter location via TOA) Lower error rates in digital communications Improved navigation capability Improved survivability and performance in radiation environment Improved survivability and performance in high shock applications Longer life, and smaller size, weight, and cost Longer recalibration interval (lower logistics costs) 1 -11

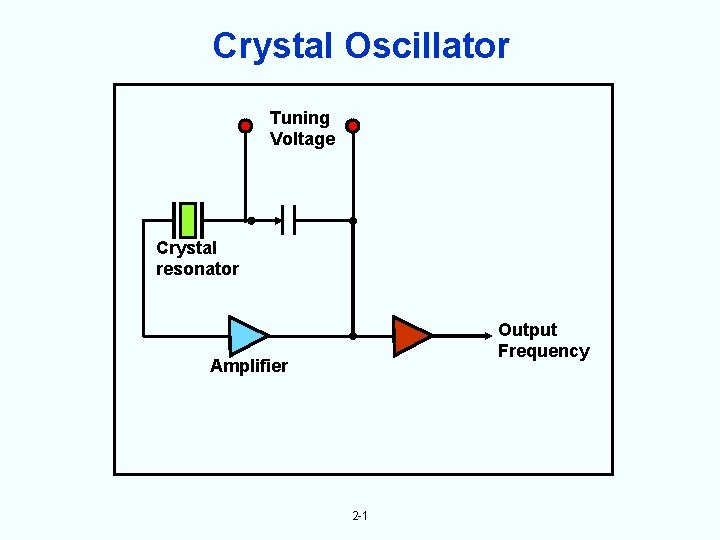
Crystal Oscillator Tuning Voltage Crystal resonator Output Frequency Amplifier 2 -1

Oscillation At the frequency of oscillation, the closed loop phase shift = 2 n. When initially energized, the only signal in the circuit is noise. That component of noise, the frequency of which satisfies the phase condition for oscillation, is propagated around the loop with increasing amplitude. The rate of increase depends on the excess; i. e. , small-signal, loop gain and on the BW of the crystal in the network. The amplitude continues to increase until the amplifier gain is reduced either by nonlinearities of the active elements ("self limiting") or by some automatic level control. At steady state, the closed-loop gain = 1. 2 -2

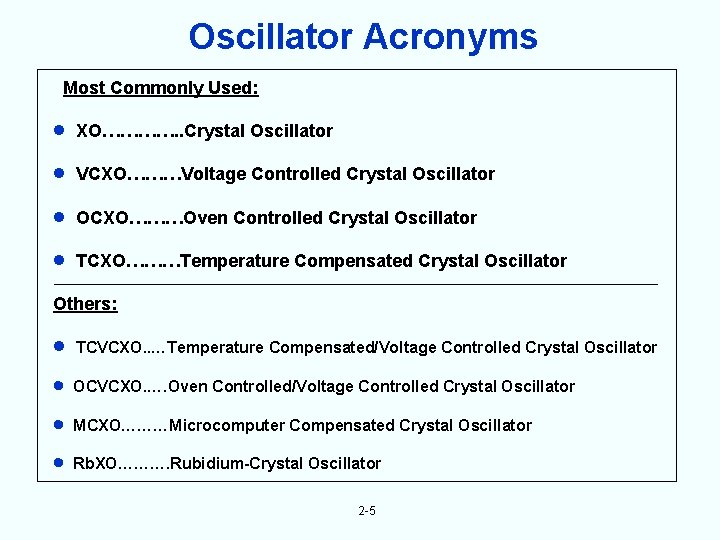
Oscillator Acronyms Most Commonly Used: XO…………. . Crystal Oscillator VCXO………Voltage Controlled Crystal Oscillator OCXO………Oven Controlled Crystal Oscillator TCXO………Temperature Compensated Crystal Oscillator Others: TCVCXO. . …Temperature Compensated/Voltage Controlled Crystal Oscillator OCVCXO. …. Oven Controlled/Voltage Controlled Crystal Oscillator MCXO………Microcomputer Compensated Crystal Oscillator Rb. XO………. Rubidium-Crystal Oscillator 2 -5

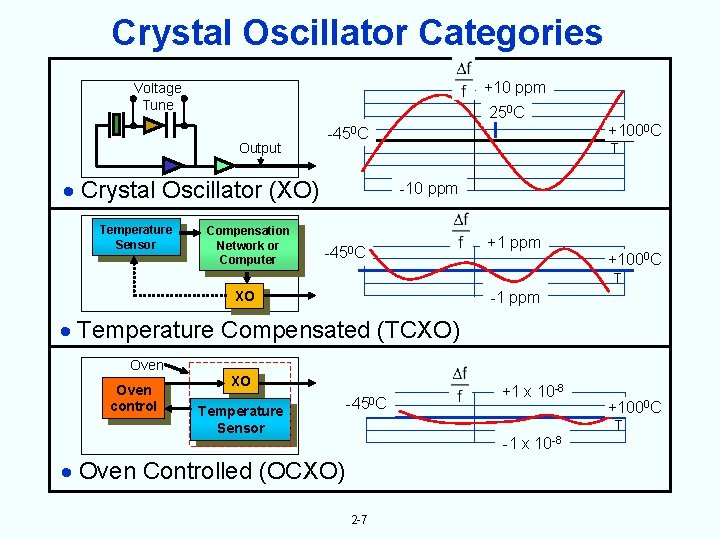
Crystal Oscillator Categories +10 ppm Voltage Tune 250 C Output Crystal Oscillator (XO) Temperature Sensor Compensation Network or Computer +1000 C -450 C T -10 ppm -450 C +1 ppm +1000 C T XO -1 ppm Temperature Compensated (TCXO) Oven control XO Temperature Sensor -450 C +1 x 10 -8 +1000 C T -1 x 10 -8 Oven Controlled (OCXO) 2 -7

Hierarchy of Oscillators Oscillator Type* Crystal oscillator (XO) Temperature compensated crystal oscillator (TCXO) Accuracy** Typical Applications 10 -5 to 10 -4 Computer timing 10 -6 Frequency control in tactical radios Microcomputer compensated 10 -8 to 10 -7 Spread spectrum system clock Oven controlled crystal oscillator (OCXO) 10 -8 (with 10 -10 per g option) Navigation system clock & frequency standard, MTI radar Small atomic frequency 10 -9 C 3 satellite terminals, bistatic, & multistatic radar High performance atomic 10 -12 to 10 -11 Strategic C 3, EW crystal oscillator (MCXO) standard (Rb, Rb. XO) standard (Cs) * Sizes range from <5 cm 3 for clock oscillators to > 30 liters for Cs standards Costs range from <$5 for clock oscillators to > $50, 000 for Cs standards. ** Including environmental effects (e. g. , -40 o. C to +75 o. C) and one year of aging. 2 -8

Why Quartz? Quartz is the only material known that possesses the following combination of properties: • Piezoelectric ("pressure-electric"; piezein = to press, in Greek) • Zero temperature coefficient cuts exist • Stress compensated cut exists • Low loss (i. e. , high Q) • Easy to process; low solubility in everything, under "normal" conditions, except the fluoride and hot alkali etchants; hard but not brittle • Abundant in nature; easy to grow in large quantities, at low cost, and with relatively high purity and perfection. Of the man-grown single crystals, quartz, at ~3, 000 tons per year, is second only to silicon in quantity grown (3 to 4 times as much Si is grown annually, as of 1997). 3 -1

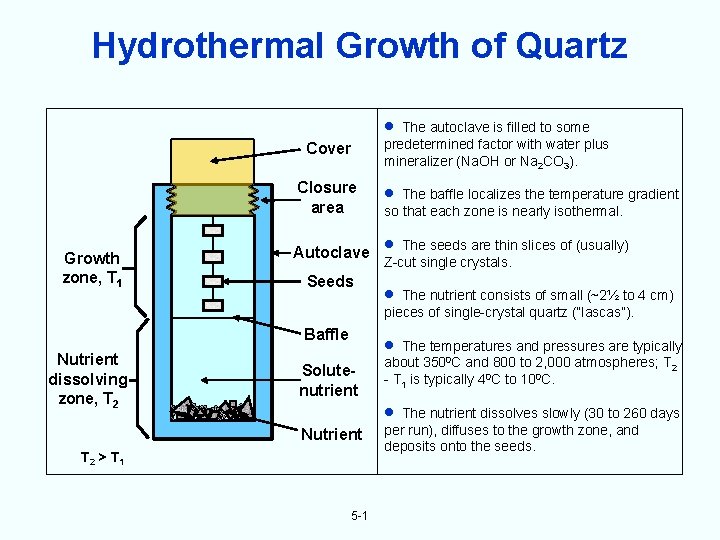
Hydrothermal Growth of Quartz The autoclave is filled to some Cover Closure area Growth zone, T 1 Autoclave Seeds predetermined factor with water plus mineralizer (Na. OH or Na 2 CO 3). The baffle localizes the temperature gradient so that each zone is nearly isothermal. The seeds are thin slices of (usually) Z-cut single crystals. The nutrient consists of small (~2½ to 4 cm) pieces of single-crystal quartz (“lascas”). Baffle Nutrient dissolving zone, T 2 The temperatures and pressures are typically Solutenutrient Nutrient T 2 > T 1 5 -1 about 3500 C and 800 to 2, 000 atmospheres; T 2 - T 1 is typically 40 C to 100 C. The nutrient dissolves slowly (30 to 260 days per run), diffuses to the growth zone, and deposits onto the seeds.

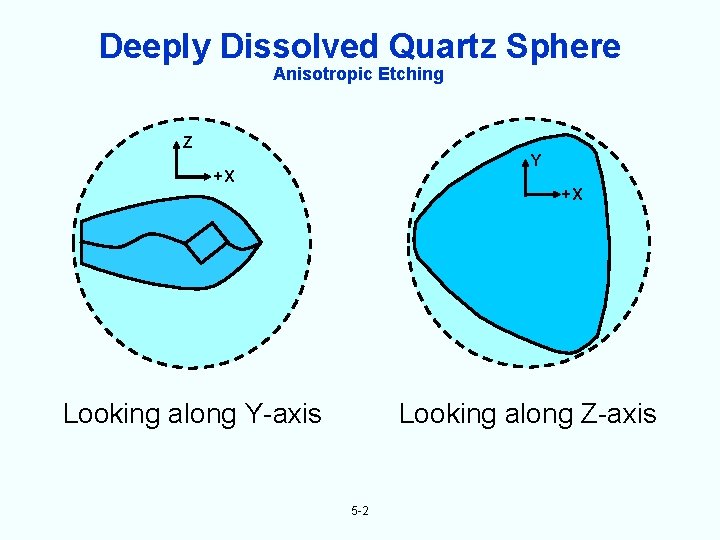
Quartz is Highly Anisotropic The properties of quartz vary greatly with crystallographic direction. For example, when a quartz sphere is etched deeply in HF, the sphere takes on a triangular shape when viewed along the Z-axis, and a lenticular shape when viewed along the Y-axis. The etching rate is more than 100 times faster along the fastest etching rate direction (the Z-direction) than along the slowest direction (the slow-X-direction). The thermal expansion coefficient is 7. 8 x 10 -6/ C along the Z- direction, and 14. 3 x 10 -6/ C perpendicular to the Z-direction; the temperature coefficient of density is, therefore, -36. 4 x 10 -6/ C. The temperature coefficients of the elastic constants range from -3300 x 10 -6/ C (for C 12) to +164 x 10 -6/ C (for C 66). For the proper angles of cut, the sum of the first two terms in Tf on the previous page is cancelled by the third term, i. e. , temperature compensated cuts exist in quartz. (See next page. ) 3 -12

Deeply Dissolved Quartz Sphere Anisotropic Etching Z Y +X +X Looking along Y-axis Looking along Z-axis 5 -2

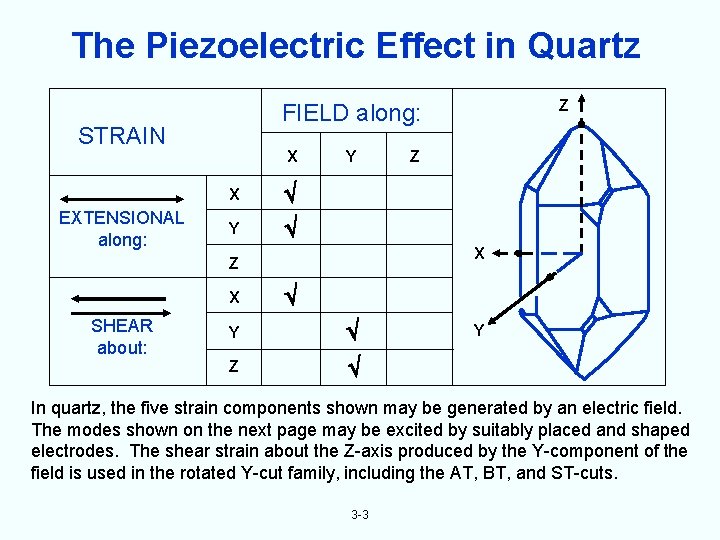
The Piezoelectric Effect in Quartz STRAIN X X EXTENSIONAL along: Y Y X Z SHEAR about: Z FIELD along: Y Z Y In quartz, the five strain components shown may be generated by an electric field. The modes shown on the next page may be excited by suitably placed and shaped electrodes. The shear strain about the Z-axis produced by the Y-component of the field is used in the rotated Y-cut family, including the AT, BT, and ST-cuts. 3 -3

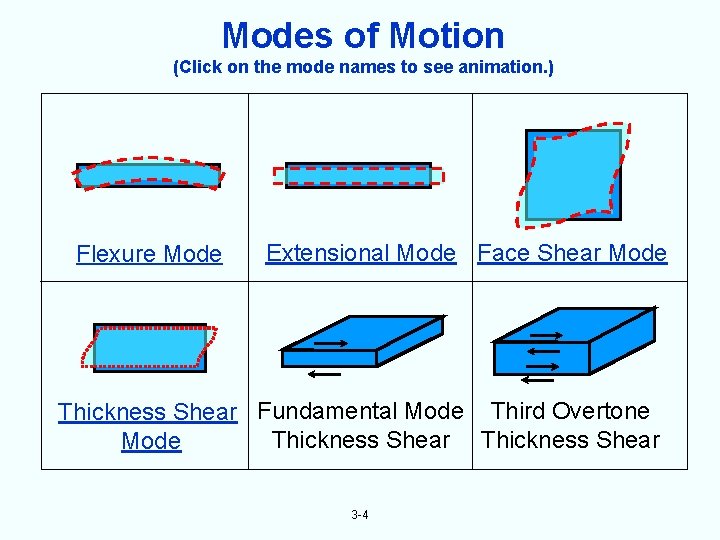
Modes of Motion (Click on the mode names to see animation. ) Flexure Mode Extensional Mode Face Shear Mode Thickness Shear Fundamental Mode Third Overtone Thickness Shear Mode 3 -4

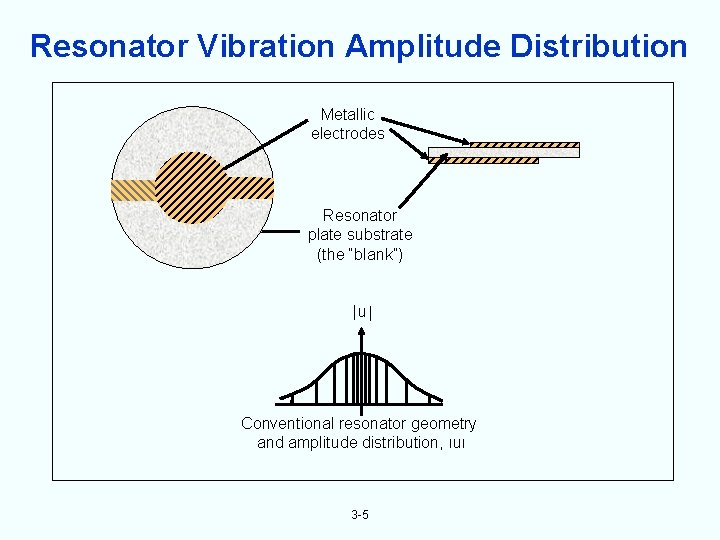
Resonator Vibration Amplitude Distribution Metallic electrodes Resonator plate substrate (the “blank”) u Conventional resonator geometry and amplitude distribution, u 3 -5

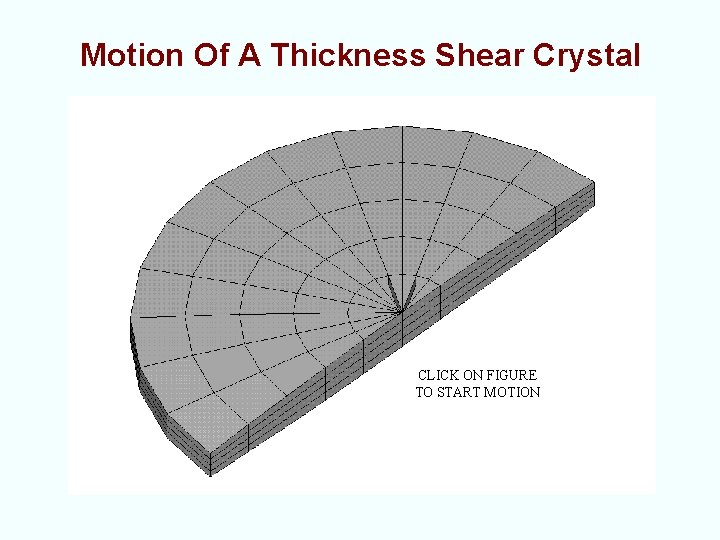
Motion Of A Thickness Shear Crystal CLICK ON FIGURE TO START MOTION

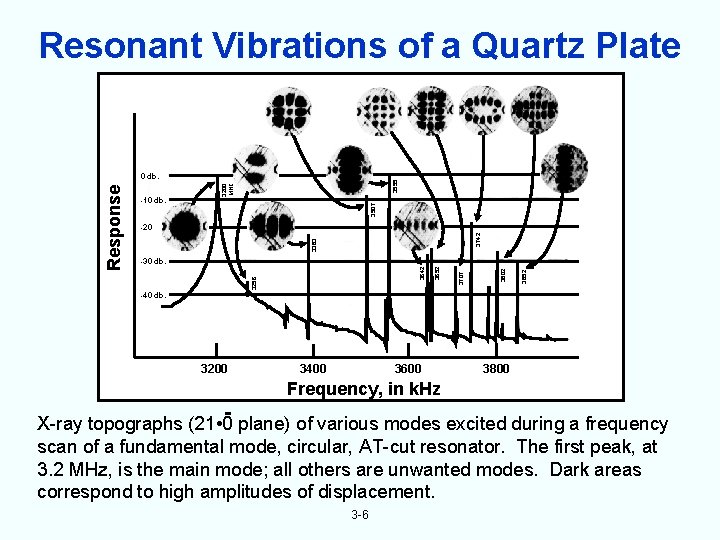
Resonant Vibrations of a Quartz Plate 3555 3507 -10 db. 3200 MHZ 3383 3742 -20 3852 3802 3707 3652 3642 -30 db. 3256 Response 0 db. -40 db. 3200 3400 3600 3800 Frequency, in k. Hz X-ray topographs (21 • 0 plane) of various modes excited during a frequency scan of a fundamental mode, circular, AT-cut resonator. The first peak, at 3. 2 MHz, is the main mode; all others are unwanted modes. Dark areas correspond to high amplitudes of displacement. 3 -6

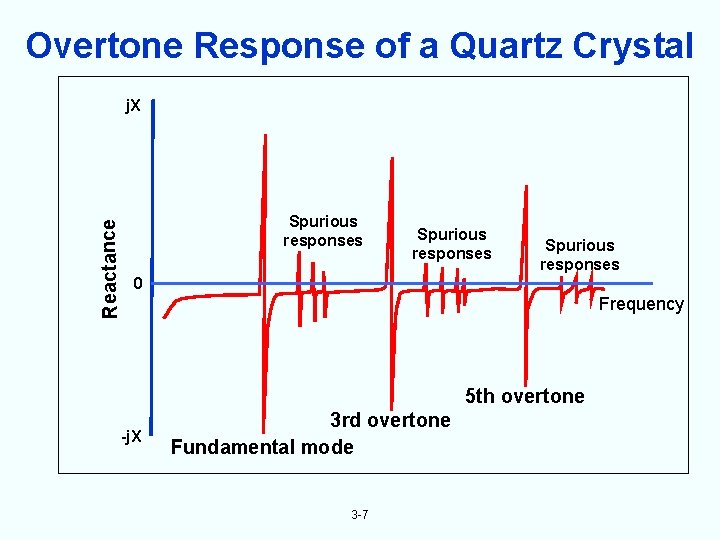
Overtone Response of a Quartz Crystal Reactance j. X Spurious responses 0 Frequency 5 th overtone -j. X 3 rd overtone Fundamental mode 3 -7

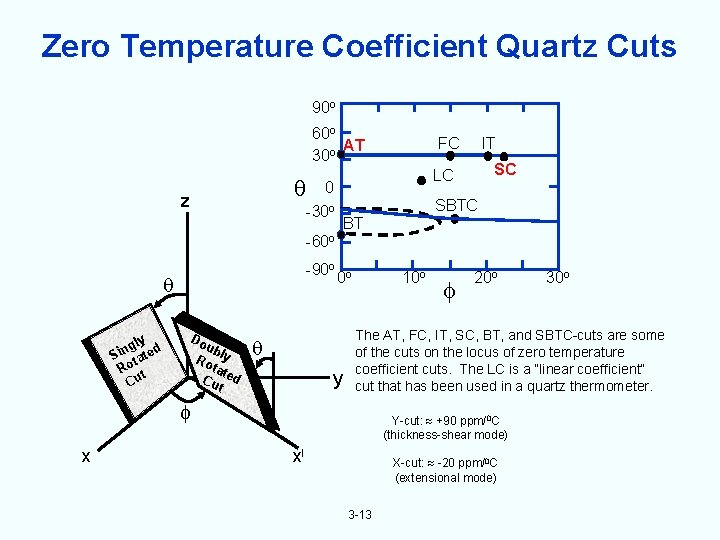
Zero Temperature Coefficient Quartz Cuts 90 o 60 o AT 30 o FC SC LC 0 -30 o z IT SBTC BT -60 o -90 o gly d n i S tate Ro t Cu Do ub Ro ly tat Cu ed t 0 o y 10 o 30 o The AT, FC, IT, SC, BT, and SBTC-cuts are some of the cuts on the locus of zero temperature coefficient cuts. The LC is a “linear coefficient” cut that has been used in a quartz thermometer. x 20 o Y-cut: +90 ppm/0 C (thickness-shear mode) xl X-cut: -20 ppm/0 C (extensional mode) 3 -13

Comparison of SC and AT-cuts Advantages of the SC-cut • Thermal transient compensated (allows faster warmup OCXO) • Static and dynamic f vs. T allow higher stability OCXO and MCXO • Better f vs. T repeatability allows higher stability OCXO and MCXO • Far fewer activity dips • Lower drive level sensitivity • Planar stress compensated; lower f due to edge forces and bending • Lower sensitivity to radiation • Higher capacitance ratio (less f for oscillator reactance changes) • Higher Q for fundamental mode resonators of similar geometry • Less sensitive to plate geometry - can use wide range of contours Disadvantage of the SC-cut : More difficult to manufacture for OCXO (but is easier to manufacture for MCXO than is an AT-cut for precision TCXO) Other Significant Differences • B-mode is excited in the SC-cut, although not necessarily in LFR's • The SC-cut is sensitive to electric fields (which can be used for compensation) 3 -14

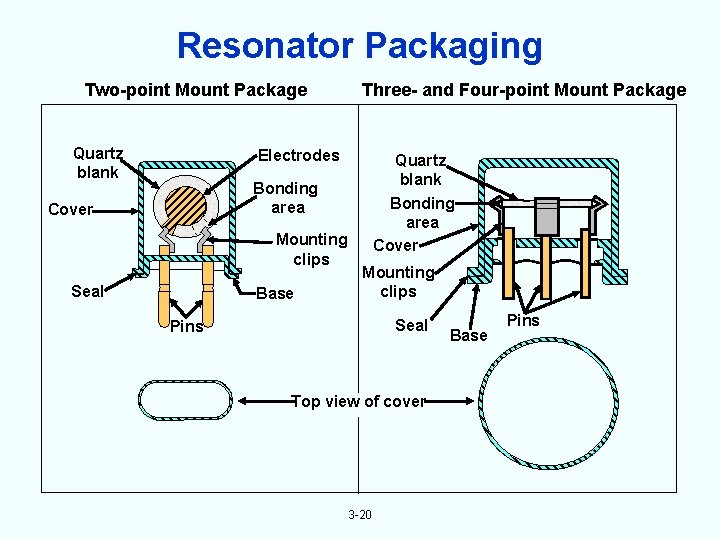
Resonator Packaging Two-point Mount Package Quartz blank Three- and Four-point Mount Package Electrodes Quartz blank Bonding area Cover Mounting clips Seal Base Bonding area Cover Mounting clips Seal Pins Top view of cover 3 -20 Base Pins

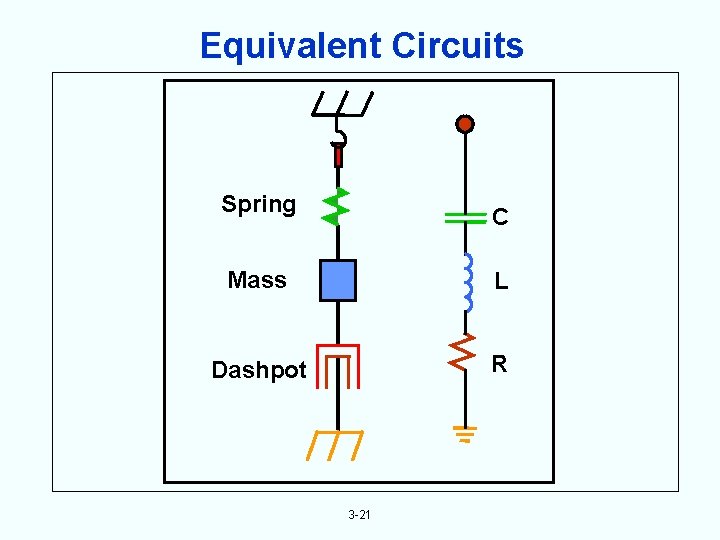
Equivalent Circuits Spring C Mass L Dashpot R 3 -21

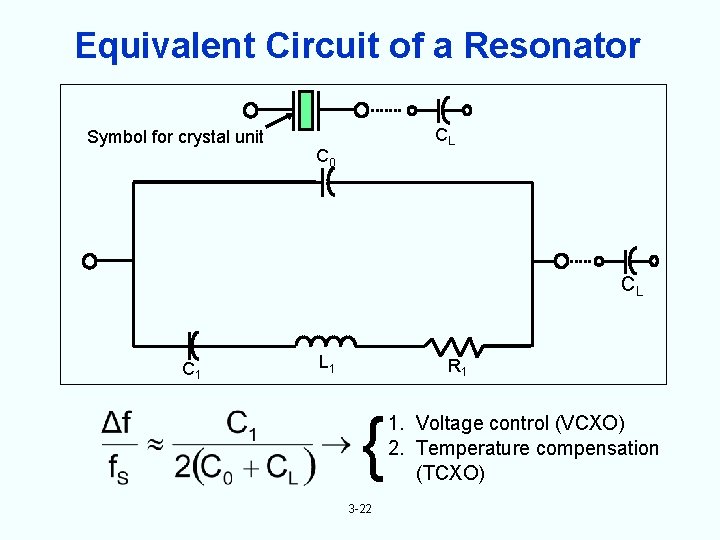
Equivalent Circuit of a Resonator Symbol for crystal unit CL C 0 CL C 1 L 1 R 1 { 3 -22 1. Voltage control (VCXO) 2. Temperature compensation (TCXO)

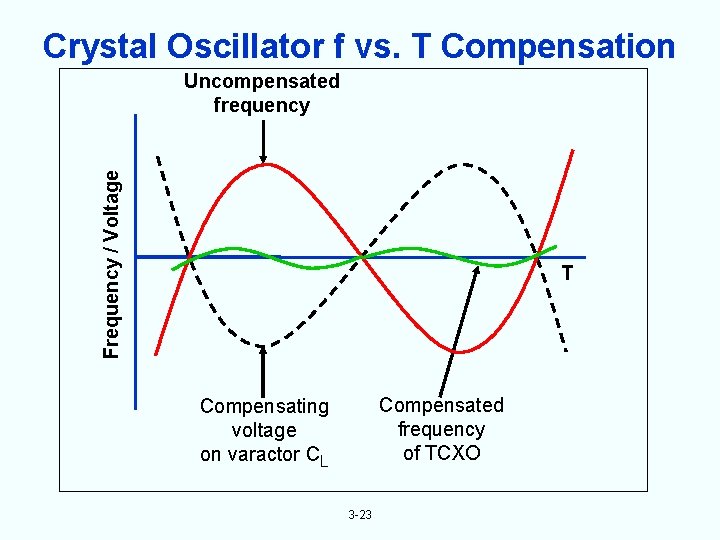
Crystal Oscillator f vs. T Compensation Frequency / Voltage Uncompensated frequency T Compensated frequency of TCXO Compensating voltage on varactor CL 3 -23

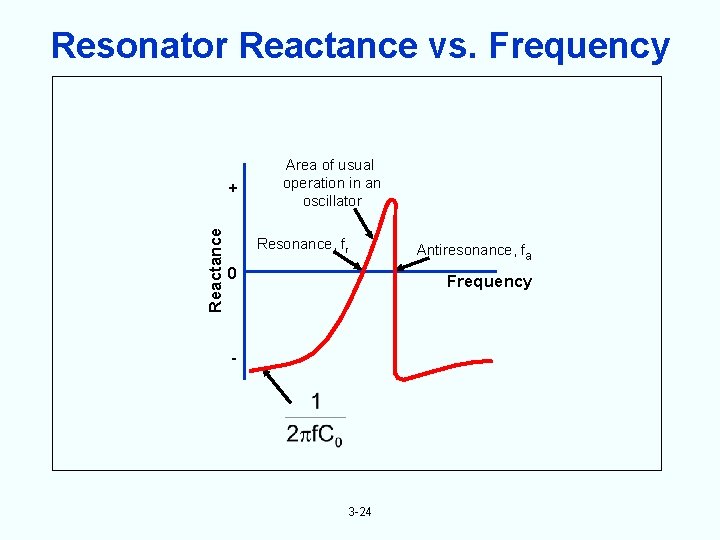
Resonator Reactance vs. Frequency Reactance + Area of usual operation in an oscillator Resonance, fr 0 Antiresonance, fa Frequency - 3 -24

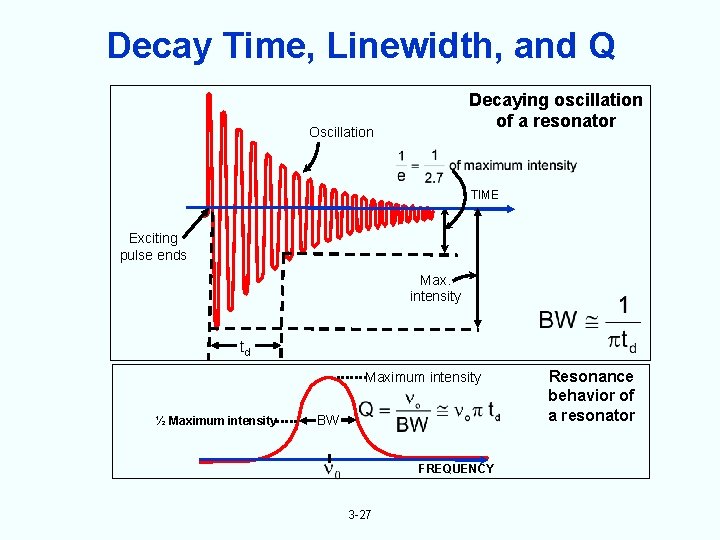
What is Q and Why is it Important? Q is proportional to the decay-time, and is inversely proportional to the linewidth of resonance (see next page). • The higher the Q, the higher the frequency stability and accuracy capability of a resonator (i. e. , high Q is a necessary but not a sufficient condition). If, e. g. , Q = 106, then 10 -10 accuracy requires ability to determine center of resonance curve to 0. 01% of the linewidth, and stability (for some averaging time) of 10 -12 requires ability to stay near peak of resonance curve to 10 -6 of linewidth. • Phase noise close to the carrier has an especially strong dependence on Q (L(f) 1/Q 4 for quartz oscillators). 3 -26

Decay Time, Linewidth, and Q Decaying oscillation of a resonator Oscillation TIME Exciting pulse ends Max. intensity td Maximum intensity ½ Maximum intensity BW FREQUENCY 3 -27 Resonance behavior of a resonator

Factors that Determine Resonator Q The maximum Q of a resonator can be expressed as: where f is the frequency in Hz, and is an empirically determined “motional time constant” in seconds, which varies with the angles of cut and the mode of vibration. For example, = 1 x 10 -14 s for the AT-cut's c-mode (Qmax = 3. 2 million at 5 MHz), = 9. 9 x 10 -15 s for the SC-cut's c-mode, and = 4. 9 x 10 -15 s for the BT-cut's b-mode. Other factors which affect the Q of a resonator include: Overtone Blank geometry (contour, Surface finish dimensional ratios) Material impurities and defects Drive level Mounting stresses Gases inside the enclosure Bonding stresses (pressure, type of gas) Temperature Interfering modes Electrode geometry and type Ionizing radiation 3 -28

Why 32, 768 Hz? 32, 768 = 215 In an analog watch, a stepping motor receives one impulse per second which advances the second hand by 6 o, i. e. , 1/60 th of a circle, every second. Dividing 32, 768 Hz by two 15 times results in 1 Hz. The 32, 768 Hz is a compromise among size, power requirement (i. e. , battery life) and stability. 3 -36 32, 768 16, 384 8, 192 4, 096 2, 048 1, 024 512 256 128 64 32 16 8 4 2 1

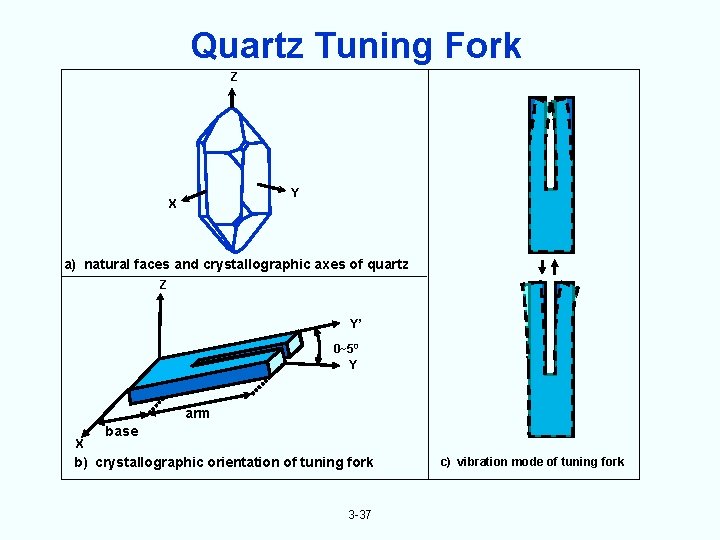
Quartz Tuning Fork Z Y X a) natural faces and crystallographic axes of quartz Z Y’ 0~50 Y arm X base b) crystallographic orientation of tuning fork 3 -37 c) vibration mode of tuning fork

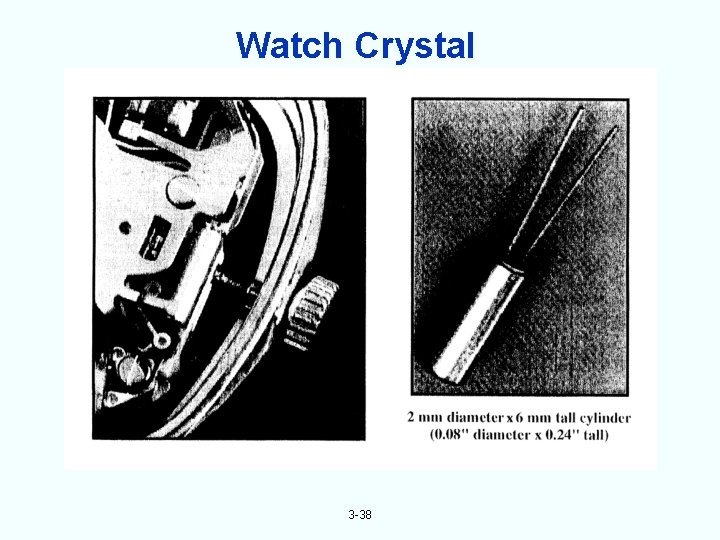
Watch Crystal 3 -38

The Units of Stability in Perspective What is one part in 1010 ? (As in 1 x 10 -10/day aging. ) ~1/2 cm out of the circumference of the earth. ~1/4 second per human lifetime (of ~80 years). Power received on earth from a GPS satellite, -160 d. BW, is as “bright” as a flashlight in Los Angeles would look in New York City, ~5000 km away (neglecting earth’s curvature). What is -170 d. B? (As in -170 d. Bc/Hz phase noise. ) -170 d. B = 1 part in 1017 thickness of a sheet of paper out of the total distance traveled by all the cars in the world in a day. 4 -1

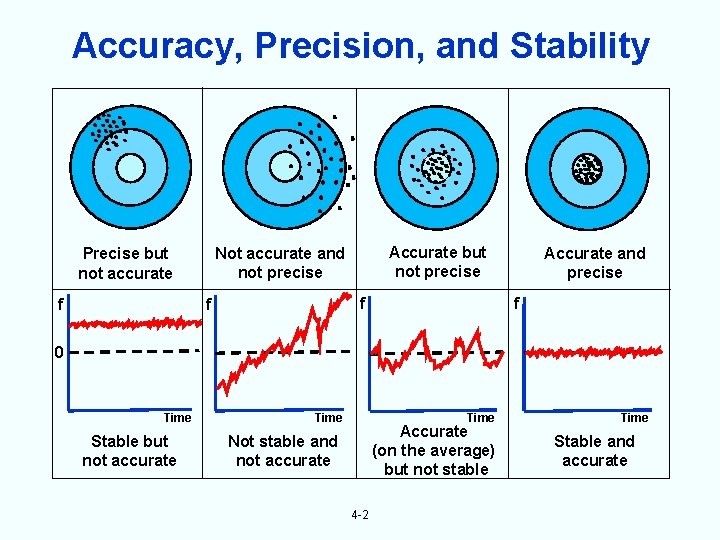
Accuracy, Precision, and Stability f Accurate but not precise Not accurate and not precise Precise but not accurate f f Accurate and precise f 0 Time Stable but not accurate Time Accurate (on the average) but not stable Not stable and not accurate 4 -2 Time Stable and accurate

Influences on Oscillator Frequency Time • Short term (noise) • Intermediate term (e. g. , due to oven fluctuations) • Long term (aging) Temperature • Static frequency vs. temperature • Dynamic frequency vs. temperature (warmup, thermal shock) • Thermal history ("hysteresis, " "retrace") Acceleration • Gravity (2 g tipover) • Vibration Ionizing radiation • Steady state • Pulsed • Acoustic noise • Shock • Photons (X-rays, -rays) • Particles (neutrons, protons, electrons) Other • Power supply voltage • Humidity • Magnetic field • Atmospheric pressure (altitude) • Load impedance 4 -3

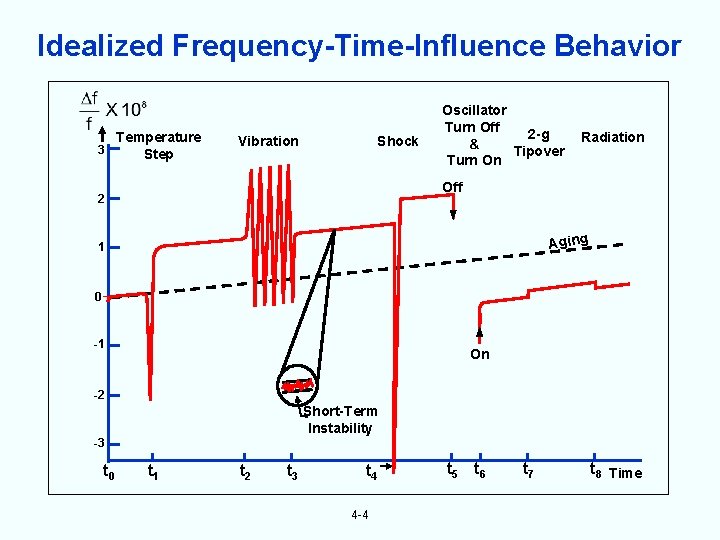
Idealized Frequency-Time-Influence Behavior 3 Temperature Step Vibration Shock Oscillator Turn Off 2 -g & Tipover Turn On Radiation Off 2 Aging 1 0 -1 On -2 Short-Term Instability -3 t 0 t 1 t 2 t 3 t 4 4 -4 t 5 t 6 t 7 t 8 Time

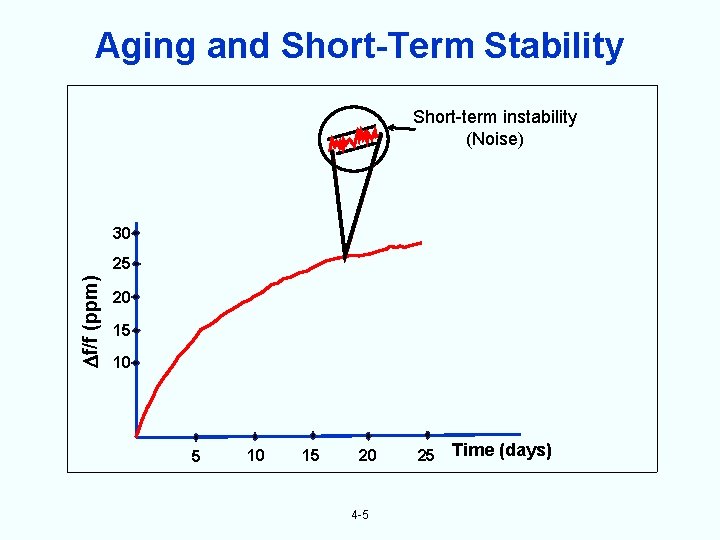
Aging and Short-Term Stability Short-term instability (Noise) 30 f/f (ppm) 25 20 15 10 15 20 4 -5 25 Time (days)

Aging Mechanisms Mass transfer due to contamination Since f 1/t, f/f = - t/t; e. g. , f 5 MHz 106 molecular layers, therefore, 1 quartz-equivalent monolayer f/f 1 ppm Stress relief in the resonator's: mounting and bonding structure, electrodes, and in the quartz (? ) Other effects Quartz outgassing Diffusion effects Chemical reaction effects Pressure changes in resonator enclosure (leaks and outgassing) Oscillator circuit aging (load reactance and drive level changes) Electric field changes (doubly rotated crystals only) Oven-control circuitry aging 4 -6

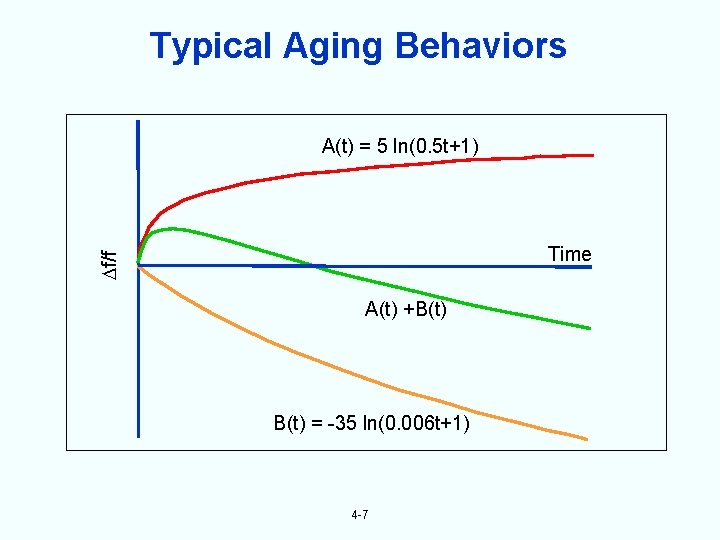
Typical Aging Behaviors A(t) = 5 ln(0. 5 t+1) f/f Time A(t) +B(t) = -35 ln(0. 006 t+1) 4 -7

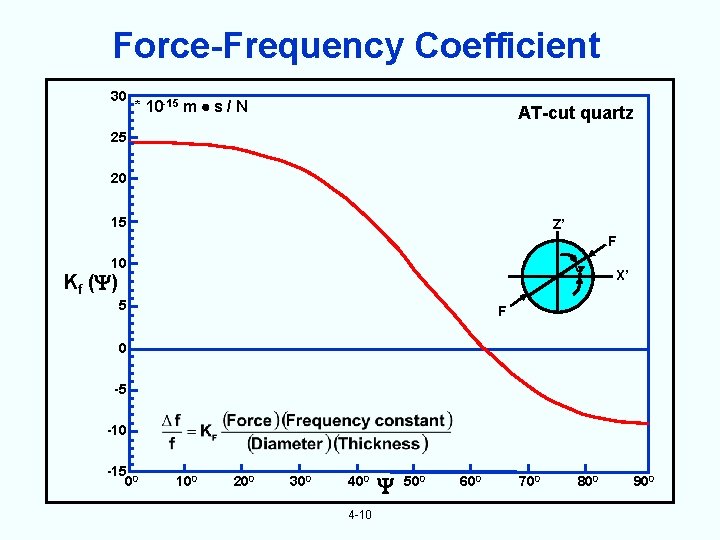
Force-Frequency Coefficient 30 * 10 -15 m s / N AT-cut quartz 25 20 15 Z’ F 10 Kf ( ) 5 X’ F 0 -5 -10 -15 0 0 100 200 300 4 -10 500 600 700 800 900

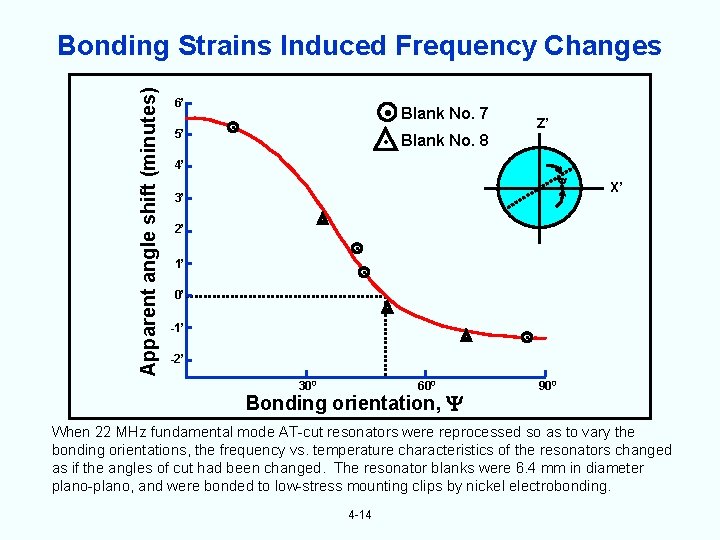
Apparent angle shift (minutes) Bonding Strains Induced Frequency Changes 6’ 5’ Blank No. 7 Z’ Blank No. 8 4’ 3’ X’ 2’ 1’ 0’ -1’ -2’ 300 600 Bonding orientation, 900 When 22 MHz fundamental mode AT-cut resonators were reprocessed so as to vary the bonding orientations, the frequency vs. temperature characteristics of the resonators changed as if the angles of cut had been changed. The resonator blanks were 6. 4 mm in diameter plano-plano, and were bonded to low-stress mounting clips by nickel electrobonding. 4 -14

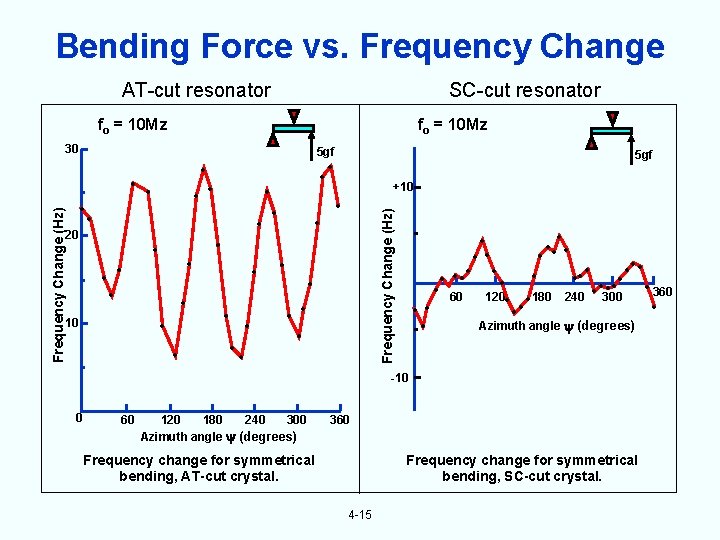
Bending Force vs. Frequency Change AT-cut resonator SC-cut resonator fo = 10 Mz 5 gf • 20 • • • • 10 • • • • 5 gf • +10 • Frequency Change (Hz) 30 • • • • • • • • • 360 • 60 120 • • 180 240 • • 300 • • Azimuth angle (degrees) • • • • -10 0 60 120 180 240 300 Azimuth angle (degrees) 360 Frequency change for symmetrical bending, AT-cut crystal. Frequency change for symmetrical bending, SC-cut crystal. 4 -15

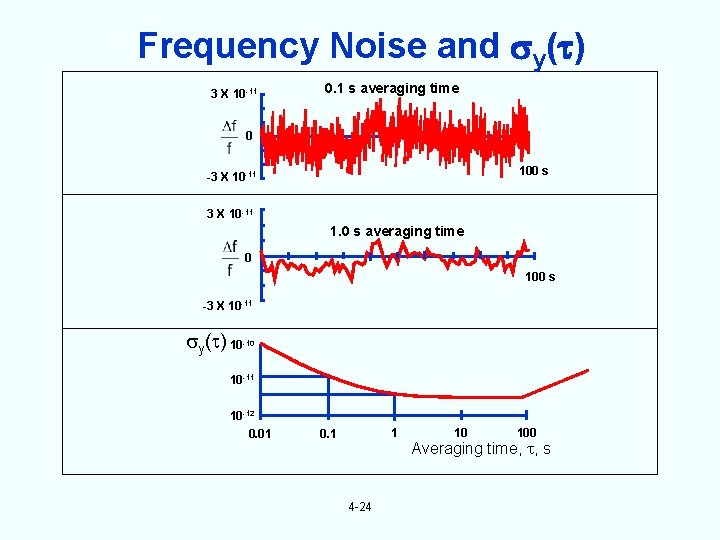
Frequency Noise and y( ) 3 X 10 -11 0. 1 s averaging time 0 100 s -3 X 10 -11 1. 0 s averaging time 0 100 s -3 X 10 -11 y( ) 10 -10 10 -11 10 -12 0. 01 1 0. 1 4 -24 10 100 Averaging time, , s

Impacts of Oscillator Noise • Limits the ability to determine the current state and the predictability of oscillators • Limits syntonization and synchronization accuracy • Limits receivers' useful dynamic range, channel spacing, and selectivity; can limit jamming resistance • Limits radar performance (especially Doppler radar's) • Causes timing errors [~ y( )] • Causes bit errors in digital communication systems • Limits number of communication system users, as noise from transmitters interfere with receivers in nearby channels • Limits navigation accuracy • Limits ability to lock to narrow-linewidth resonances • Can cause loss of lock; can limit acquisition/reacquisition capability in phase-locked-loop systems 4 -18

Causes of Short Term Instabilities Johnson noise (thermally induced charge fluctuations, i. e. , "thermal emf” in resistive elements) Phonon scattering by defects & quantum fluctuations (related to Q) Noise due to oscillator circuitry (active and passive components) Temperature fluctuations- thermal transient effects - activity dips at oven set-point Random vibration Fluctuations in the number of adsorbed molecules Stress relief, fluctuations at interfaces (quartz, electrode, mount, bond) Shot noise in atomic frequency standards ? ? ? 4 -19

Noise in Crystal Oscillators The resonator is the primary noise source close to the carrier; the oscillator sustaining circuitry is the primary source far from the carrier. Frequency multiplication by N increases the phase noise by N 2 (i. e. , by 20 log N, in d. B's). Vibration-induced "noise" dominates all other sources of noise in many applications (see acceleration effects section, later). Close to the carrier (within BW of resonator), Sy(f) varies as 1/f, S (f) as 1/f 3, where f = offset from carrier frequency, . S (f) also varies as 1/Q 4, where Q = unloaded Q. Since Qmax = const. , S (f) 4. (Qmax )BAW = 1. 6 x 1013 Hz; (Qmax )SAW = 1. 05 x 1013 Hz. In the time domain, noise floor is y( ) (2. 0 x 10 -7)Q-1 1. 2 x 10 -20 , in Hz. In the regions where y( ) varies as -1 and -1/2 ( -1/2 occurs in atomic frequency standards), y( ) (QSR)-1, where SR is the signal-to-noise ratio; i. e. , the higher the Q and the signal to-noise ratio, the better the short term stability (and the phase noise far from the carrier, in the frequency domain). It is the loaded Q of the resonator that affects the noise when the oscillator sustaining circuitry is a significant noise source. Noise floor is limited by Johnson noise; noise power, k. T = -174 d. Bm/Hz at 290 K. Higher signal level improves the noise floor but not the close-in noise. (In fact, high drive levels generally degrade the close-in noise, for reasons that are not fully understood. ) Low noise SAW vs. low noise BAW multiplied up: BAW is lower noise at f < ~1 k. Hz, SAW is lower noise at f > ~1 k. Hz; can phase lock the two to get the best of both. 4 -36

TCXO Noise The short term stabilities of TCXOs are temperature (T) dependent, and are generally worse than those of OCXOs, for the following reasons: The slope of the TCXO crystal’s frequency (f) vs. T varies with T. For example, the f vs. T slope may be near zero at ~20 o. C, but it will be ~1 ppm/o. C at the T extremes. T fluctuations will cause small f fluctuations at laboratory ambient T’s, so the stability can be good there, but millidegree fluctuations will cause ~10 -9 f fluctuations at the T extremes. The TCXO’s f vs. T slopes also vary with T; the zeros and maxima can be at any T, and the maximum slopes can be on the order of 1 ppm/o. C. AT-cut crystals’ thermal transient sensitivity makes the effects of T fluctuations depend not only on the T but also on the rate of change of T (whereas the SC-cut crystals typically used in precision OCXOs are insensitive to thermal transients). Under changing T conditions, the T gradient between the T sensor (thermistor) and the crystal will aggravate the problems. TCXOs typically use fundamental mode AT-cut crystals which have lower Q and larger C 1 than the crystals typically used in OCXOs. The lower Q makes the crystals inherently noisier, and the larger C 1 makes the oscillators more susceptible to circuitry noise. AT-cut crystals’ f vs. T often exhibit activity dips (see “Activity Dips” later in this chapter). At the T’s where the dips occur, the f vs. T slope can be very high, so the noise due to T fluctuations will also be very high, e. g. , 100 x degradation of y( ) and 30 d. B degradation of phase noise are possible. Activity dips can occur at any T. 4 -40

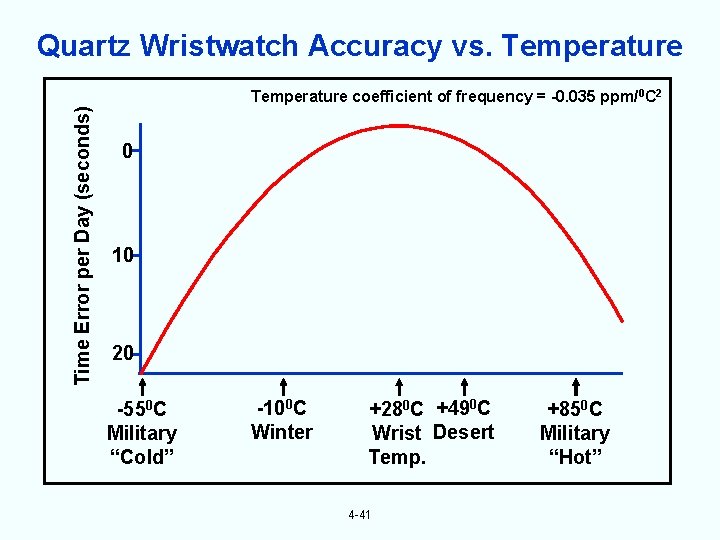
Quartz Wristwatch Accuracy vs. Temperature Time Error per Day (seconds) Temperature coefficient of frequency = -0. 035 ppm/0 C 2 0 10 20 -550 C Military “Cold” -100 C Winter +280 C +490 C Wrist Desert Temp. 4 -41 +850 C Military “Hot”

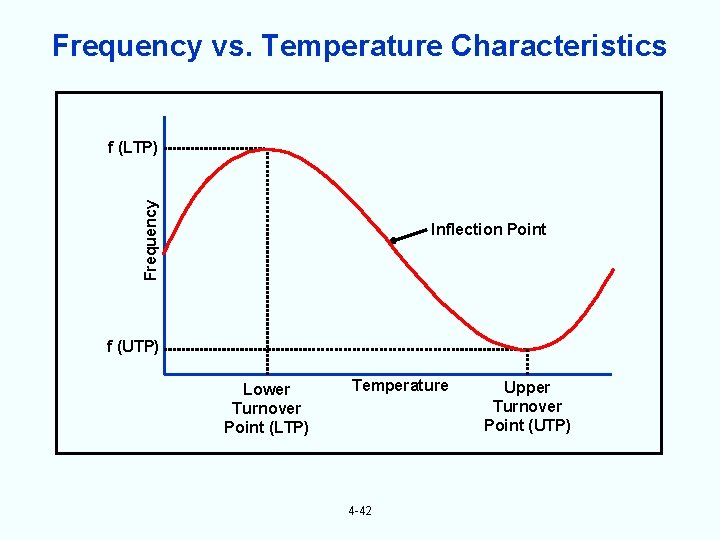
Frequency vs. Temperature Characteristics Frequency f (LTP) Inflection Point f (UTP) Lower Turnover Point (LTP) Temperature 4 -42 Upper Turnover Point (UTP)

Resonator f vs. T Determining Factors Primary: Angles of cut Secondary: • Overtone • Blank geometry (contour, dimensional ratios) • Material impurities and strains • Mounting & bonding stresses (magnitude and direction) • Electrodes (size, shape, thickness, density, stress) • Drive level • Interfering modes • Load reactance (value & temperature coefficient) • Temperature rate of change • Thermal history • Ionizing radiation 4 -43

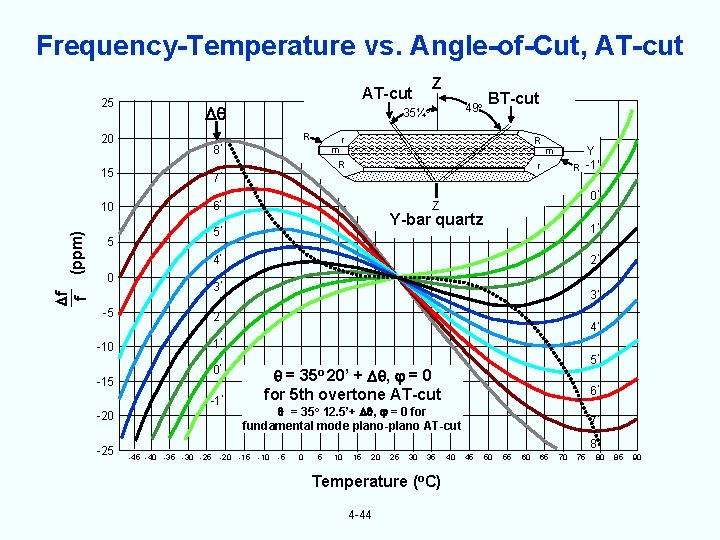
Frequency-Temperature vs. Angle-of-Cut, AT-cut 25 (ppm) f f 7’ 10 6’ R Y R -1’ m r 0’ Z Y-bar quartz 5’ 5 BT-cut r m R 8’ 15 49 o 35¼o R 20 Z AT-cut 1’ 4’ 0 3’ -5 3’ 2’ 4’ 1’ -10 0’ -15 -1’ -20 -25 2’ 5’ = 35 o 20’ + , = 0 for 5 th overtone AT-cut 6’ = 35 o 12. 5’+ , = 0 for fundamental mode plano-plano AT-cut 7’ 8’ -45 -40 -35 -30 -25 -20 -15 -10 -5 0 5 10 15 20 25 30 35 Temperature (o. C) 4 -44 40 45 50 55 60 65 70 75 80 85 90

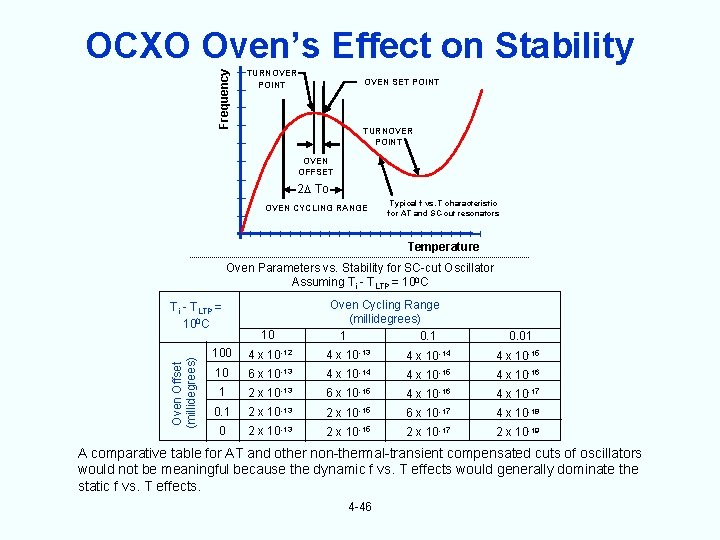
Frequency OCXO Oven’s Effect on Stability TURNOVER POINT OVEN SET POINT TURNOVER POINT OVEN OFFSET 2 To OVEN CYCLING RANGE Typical f vs. T characteristic for AT and SC-cut resonators Temperature Oven Parameters vs. Stability for SC-cut Oscillator Assuming Ti - TLTP = 100 C 10 Oven Cycling Range (millidegrees) 1 0. 01 100 4 x 10 -12 4 x 10 -13 4 x 10 -14 4 x 10 -15 10 6 x 10 -13 4 x 10 -14 4 x 10 -15 4 x 10 -16 1 2 x 10 -13 6 x 10 -15 4 x 10 -16 4 x 10 -17 0. 1 2 x 10 -13 2 x 10 -15 6 x 10 -17 4 x 10 -18 0 2 x 10 -13 2 x 10 -15 2 x 10 -17 2 x 10 -19 Oven Offset (millidegrees) Ti - TLTP = 100 C A comparative table for AT and other non-thermal-transient compensated cuts of oscillators would not be meaningful because the dynamic f vs. T effects would generally dominate the static f vs. T effects. 4 -46

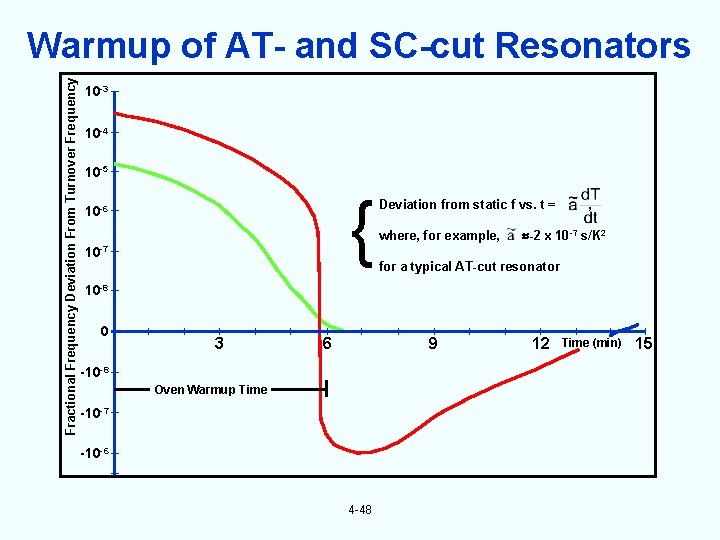
Fractional Frequency Deviation From Turnover Frequency Warmup of AT- and SC-cut Resonators 10 -3 10 -4 10 -5 { 10 -6 10 -7 Deviation from static f vs. t = where, for example, , -2 x 10 -7 s/K 2 for a typical AT-cut resonator 10 -8 0 3 6 9 -10 -8 Oven Warmup Time -10 -7 -10 -6 4 -48 12 Time (min) 15

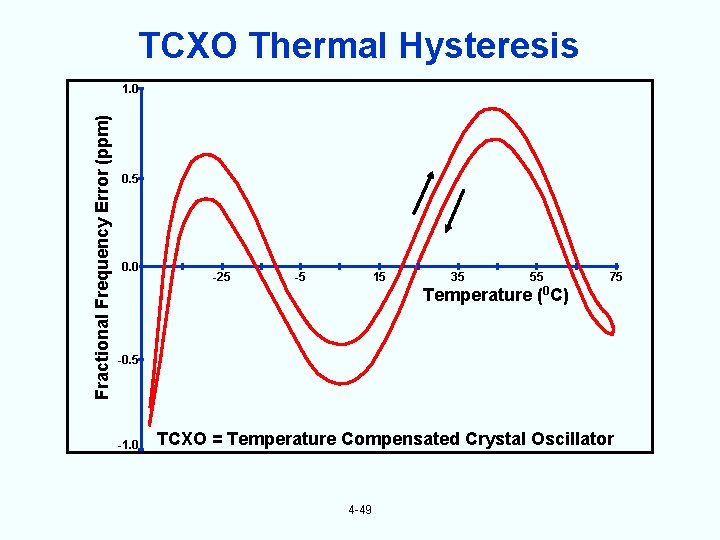
TCXO Thermal Hysteresis Fractional Frequency Error (ppm) 1. 0 0. 5 0. 0 -25 -5 15 35 55 Temperature (0 C) 75 -0. 5 -1. 0 TCXO = Temperature Compensated Crystal Oscillator 4 -49

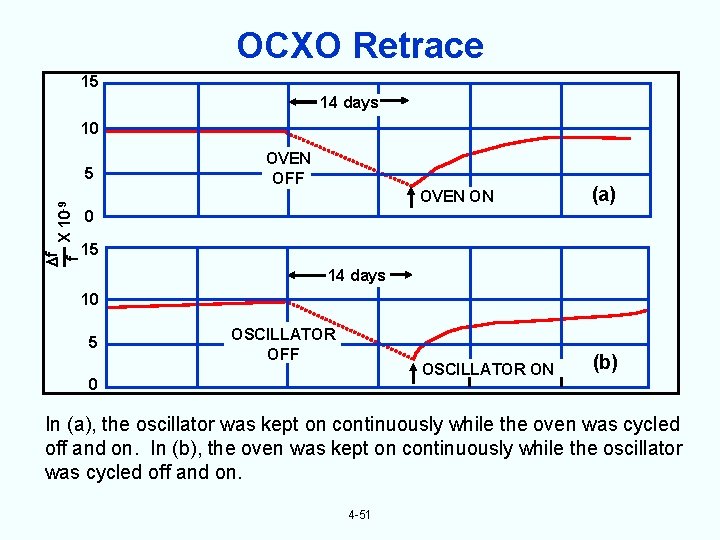
OCXO Retrace 15 14 days 10 f -9 f X 10 5 OVEN OFF OVEN ON (a) OSCILLATOR ON (b) 0 15 14 days 10 5 OSCILLATOR OFF 0 In (a), the oscillator was kept on continuously while the oven was cycled off and on. In (b), the oven was kept on continuously while the oscillator was cycled off and on. 4 -51

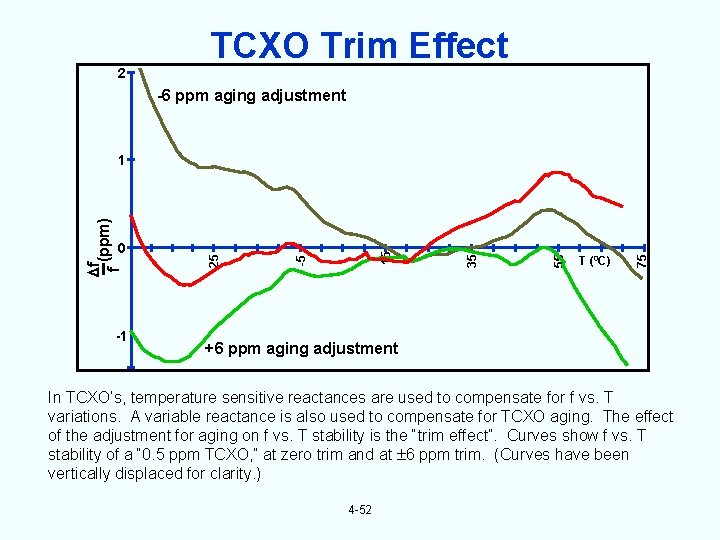
2 TCXO Trim Effect -6 ppm aging adjustment -1 T (0 C) 75 55 35 15 -5 0 -25 f (ppm) f 1 +6 ppm aging adjustment In TCXO’s, temperature sensitive reactances are used to compensate for f vs. T variations. A variable reactance is also used to compensate for TCXO aging. The effect of the adjustment for aging on f vs. T stability is the “trim effect”. Curves show f vs. T stability of a “ 0. 5 ppm TCXO, ” at zero trim and at 6 ppm trim. (Curves have been vertically displaced for clarity. ) 4 -52

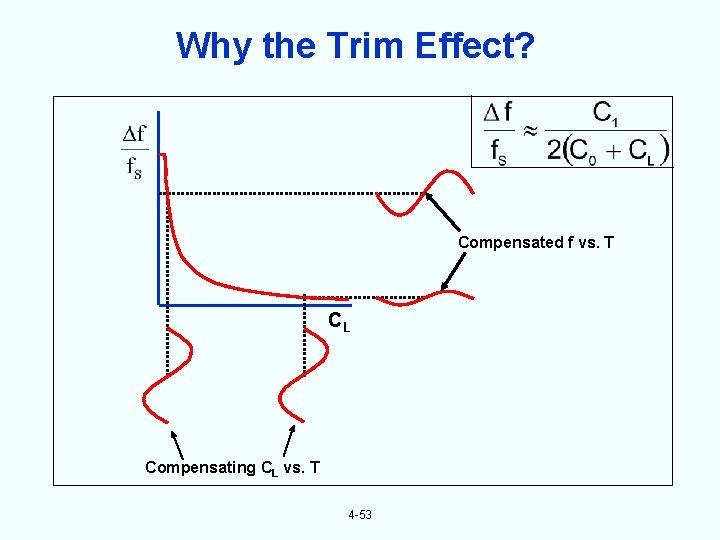
Why the Trim Effect? Compensated f vs. T CL Compensating CL vs. T 4 -53

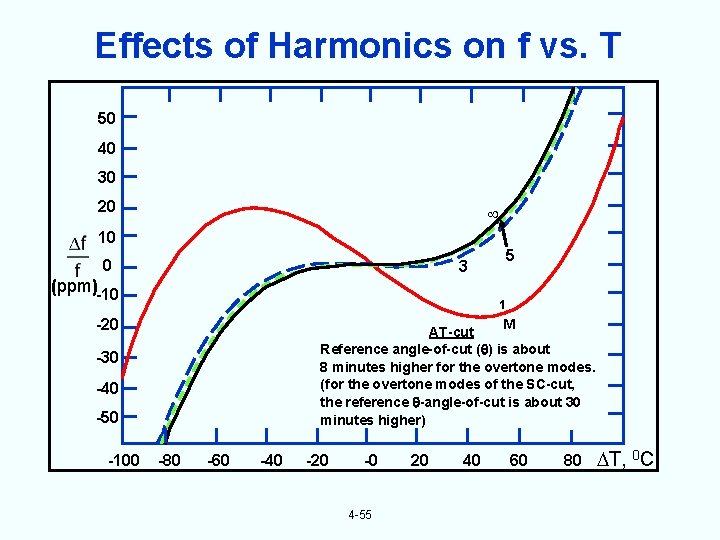
Effects of Harmonics on f vs. T 50 40 30 20 10 0 3 (ppm)-10 1 -20 M AT-cut Reference angle-of-cut ( ) is about 8 minutes higher for the overtone modes. (for the overtone modes of the SC-cut, the reference -angle-of-cut is about 30 minutes higher) -30 -40 -50 -100 5 -80 -60 -40 -20 -0 4 -55 20 40 60 80 T, 0 C

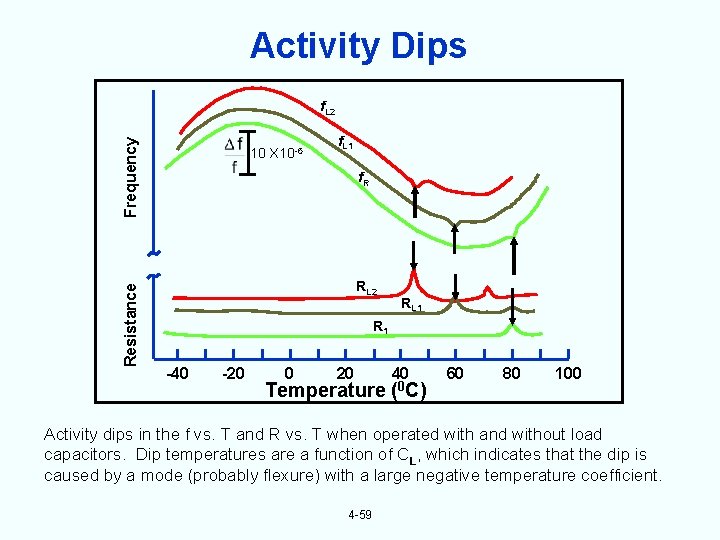
Activity Dips Resistance Frequency f. L 2 10 X 10 -6 f. L 1 f. R RL 2 RL 1 R 1 -40 -20 0 20 Temperature 40 (0 C) 60 80 100 Activity dips in the f vs. T and R vs. T when operated with and without load capacitors. Dip temperatures are a function of CL, which indicates that the dip is caused by a mode (probably flexure) with a large negative temperature coefficient. 4 -59

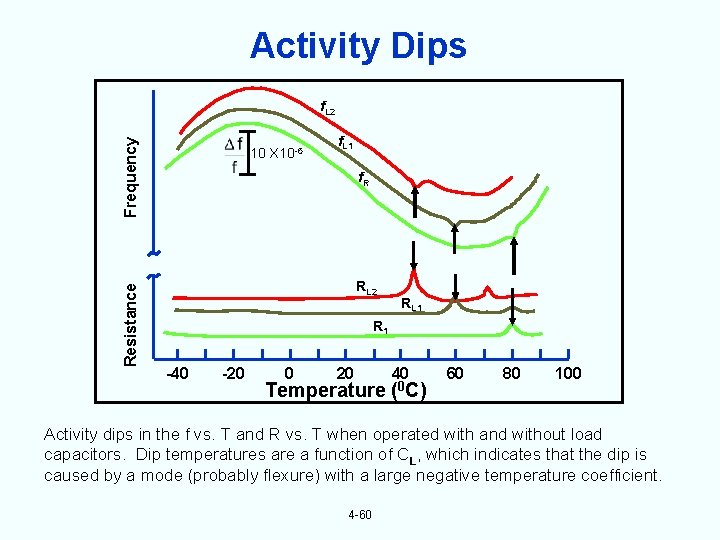
Activity Dips Resistance Frequency f. L 2 10 X 10 -6 f. L 1 f. R RL 2 RL 1 R 1 -40 -20 0 20 Temperature 40 (0 C) 60 80 100 Activity dips in the f vs. T and R vs. T when operated with and without load capacitors. Dip temperatures are a function of CL, which indicates that the dip is caused by a mode (probably flexure) with a large negative temperature coefficient. 4 -60

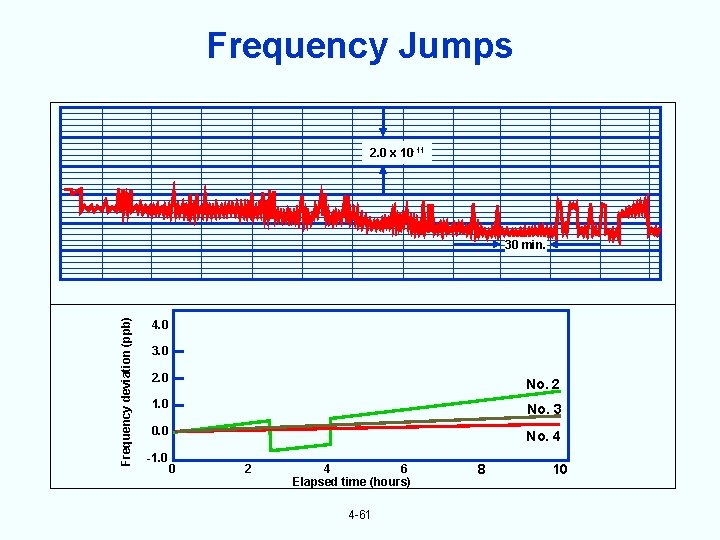
Frequency Jumps 2. 0 x 10 -11 Frequency deviation (ppb) 30 min. 4. 0 3. 0 2. 0 No. 2 1. 0 No. 3 0. 0 No. 4 -1. 0 0 2 4 6 Elapsed time (hours) 4 -61 8 10

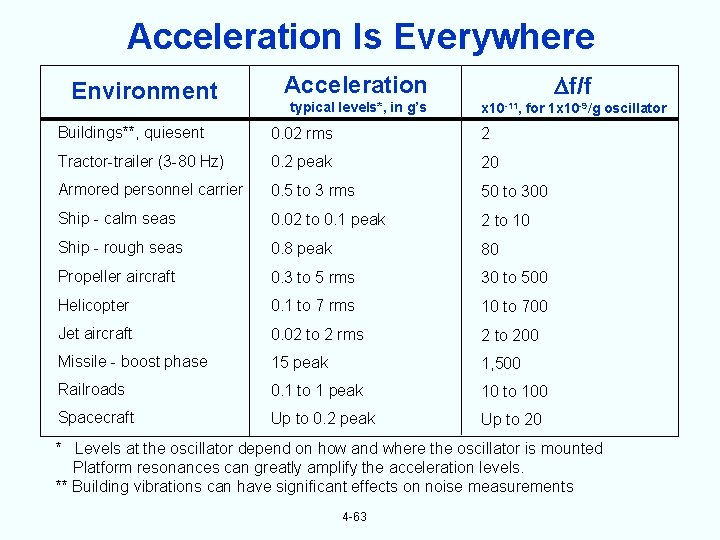
Acceleration Is Everywhere f/f Environment Acceleration Buildings**, quiesent 0. 02 rms 2 Tractor-trailer (3 -80 Hz) 0. 2 peak 20 Armored personnel carrier 0. 5 to 3 rms 50 to 300 Ship - calm seas 0. 02 to 0. 1 peak 2 to 10 Ship - rough seas 0. 8 peak 80 Propeller aircraft 0. 3 to 5 rms 30 to 500 Helicopter 0. 1 to 7 rms 10 to 700 Jet aircraft 0. 02 to 2 rms 2 to 200 Missile - boost phase 15 peak 1, 500 Railroads 0. 1 to 1 peak 10 to 100 Spacecraft Up to 0. 2 peak Up to 20 typical levels*, in g’s x 10 -11, for 1 x 10 -9/g oscillator * Levels at the oscillator depend on how and where the oscillator is mounted Platform resonances can greatly amplify the acceleration levels. ** Building vibrations can have significant effects on noise measurements 4 -63

Acceleration Affects “Everything” Acceleration Force Deformation (strain) Change in material and device properties - to some level Examples: - Quartz resonator frequency - Amplifier gain (strain changes semiconductor band structure) - Laser diode emission frequencies - Optical properties - fiber index of refraction (acoustooptics) - Cavity frequencies - DRO frequency (strain changes dielectric constants) - Atomic clock frequencies - Stray reactances - Clock rates (relativistic effects) 4 -634

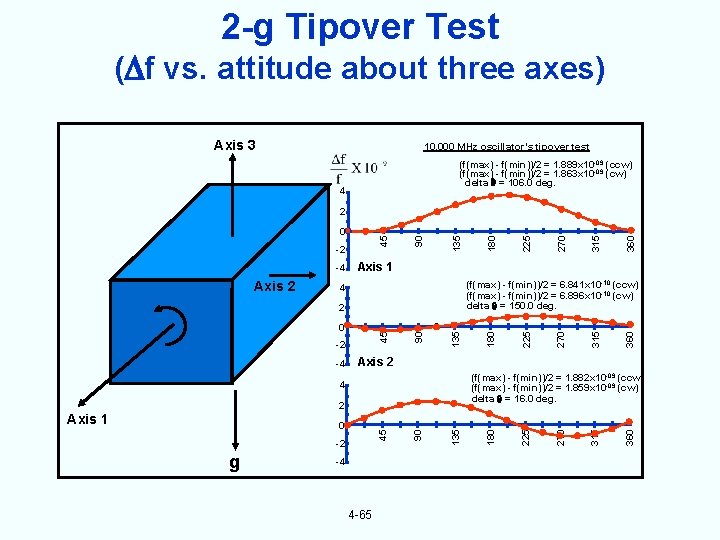
2 -g Tipover Test ( f vs. attitude about three axes) Axis 3 10. 000 MHz oscillator’s tipover test (f(max) - f(min))/2 = 1. 889 x 10 -09 (ccw) (f(max) - f(min))/2 = 1. 863 x 10 -09 (cw) delta = 106. 0 deg. 4 g -4 4 -65 360 270 315 360 315 -2 135 45 0 90 2 270 (f(max) - f(min))/2 = 1. 882 x 10 -09 (ccw) (f(max) - f(min))/2 = 1. 859 x 10 -09 (cw) delta = 16. 0 deg. 4 Axis 1 225 Axis 2 225 -4 270 -2 135 45 0 90 2 225 (f(max) - f(min))/2 = 6. 841 x 10 -10 (ccw) (f(max) - f(min))/2 = 6. 896 x 10 -10 (cw) delta = 150. 0 deg. 4 180 Axis 2 Axis 1 180 -4 180 -2 135 45 0 90 2

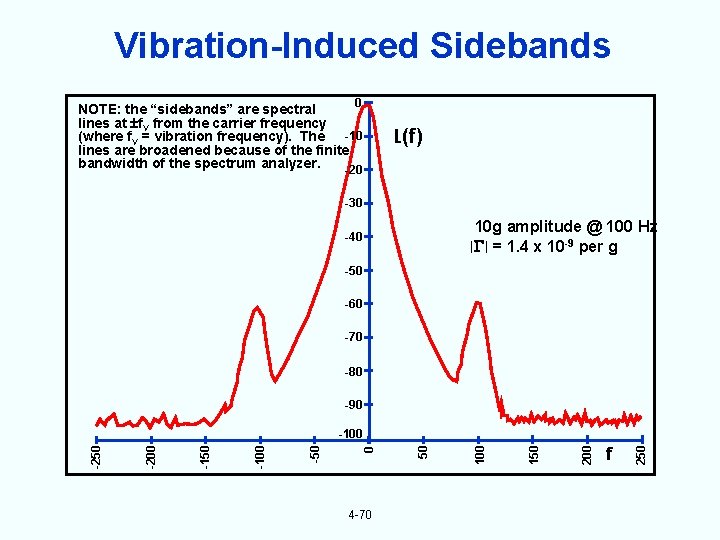
Vibration-Induced Sidebands 0 NOTE: the “sidebands” are spectral lines at f. V from the carrier frequency (where f. V = vibration frequency). The -10 lines are broadened because of the finite bandwidth of the spectrum analyzer. -20 L(f) -30 10 g amplitude @ 100 Hz = 1. 4 x 10 -9 per g -40 -50 -60 -70 -80 -90 4 -70 f 250 200 150 100 50 0 -50 -100 -150 -200 -250 -100

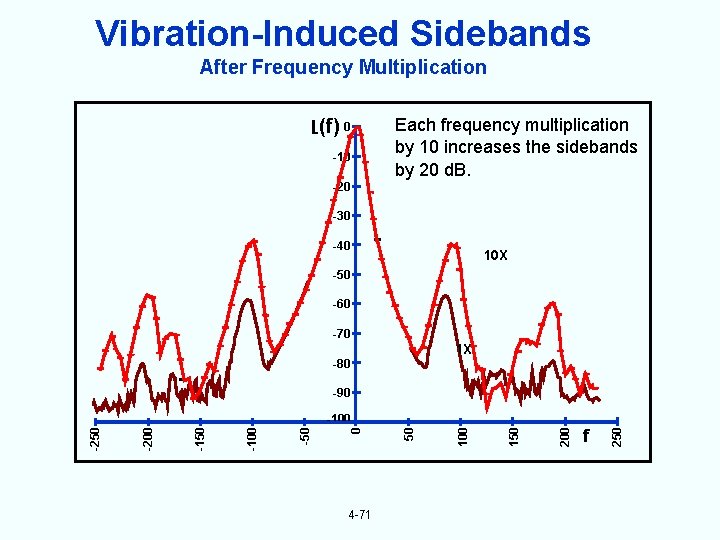
Vibration-Induced Sidebands After Frequency Multiplication L(f) 0 -10 -20 Each frequency multiplication by 10 increases the sidebands by 20 d. B. -30 -40 10 X -50 -60 -70 1 X -80 -90 4 -71 f 250 200 150 100 50 0 -50 -100 -150 -200 -250 -100

Sine Vibration-Induced Phase Noise Sinusoidal vibration produces spectral lines at fv from the carrier, where fv is the vibration frequency. e. g. , if = 1 x 10 -9/g and f 0 = 10 MHz, then even if the oscillator is completely noise free at rest, the phase “noise” i. e. , the spectral lines, due solely to a sine vibration level of 1 g will be; Vibr. freq. , fv, in Hz 100 1, 000 10, 000 4 -72 L’(fv), in d. Bc -46 -66 -86 -106 -126

Random Vibration-Induced Phase Noise Random vibration’s contribution to phase noise is given by: e. g. , if = 1 x 10 -9/g and f 0 = 10 MHz, then even if the oscillator is completely noise free at rest, the phase “noise” i. e. , the spectral lines, due solely to a vibration of power spectral density, PSD = 0. 1 g 2/Hz will be: Offset freq. , f, in Hz 100 1, 000 10, 000 4 -73 L’(f), in d. Bc/Hz -53 -73 -93 -113 -133

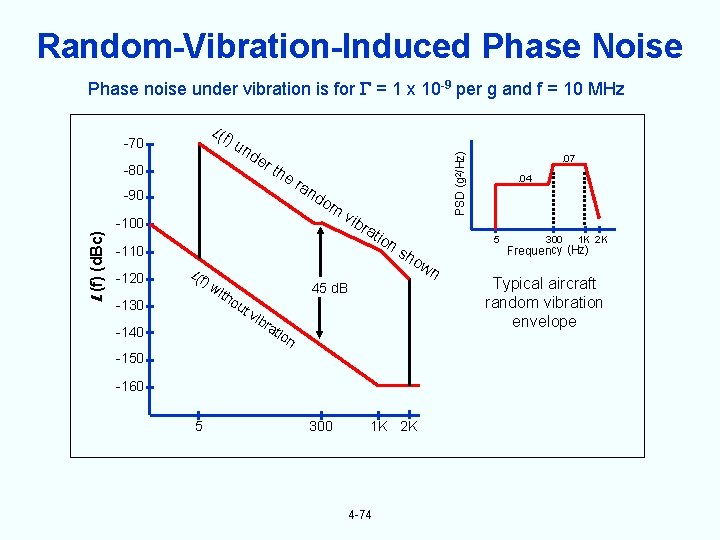
Random-Vibration-Induced Phase Noise L(f ) u -70 -80 nd er the ra L (f) (d. Bc) -90 nd om vi -100 bra t ion -110 -120 -130 ) w ith ou 45 d. B t v ibr ati on -150 -160 5 300 1 K 2 K 4 -74 . 07. 04 5 sh ow n L(f -140 PSD (g 2/Hz) Phase noise under vibration is for = 1 x 10 -9 per g and f = 10 MHz 300 1 K 2 K Frequency (Hz) Typical aircraft random vibration envelope

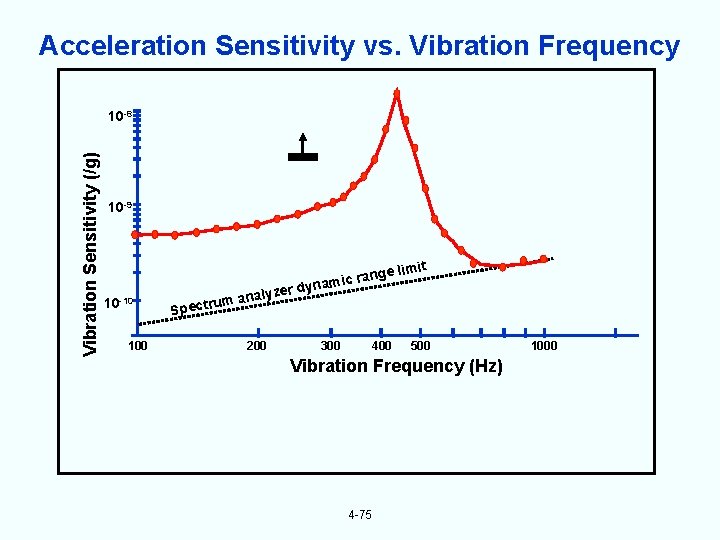
Acceleration Sensitivity vs. Vibration Frequency Vibration Sensitivity (/g) 10 -8 10 -9 10 -10 100 e limit g n a r amic er dyn nalyz trum a Spec 200 300 400 500 Vibration Frequency (Hz) 4 -75 1000

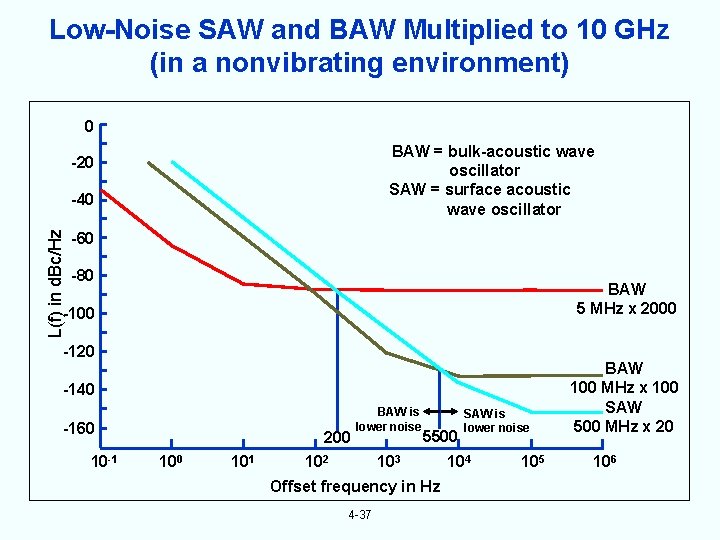
Low-Noise SAW and BAW Multiplied to 10 GHz (in a nonvibrating environment) 0 BAW = bulk-acoustic wave oscillator SAW = surface acoustic wave oscillator -20 L(f) in d. Bc/Hz -40 -60 -80 BAW 5 MHz x 2000 -120 -140 -160 10 -1 200 101 BAW is lower noise 102 5500 103 Offset frequency in Hz 4 -37 SAW is lower noise 104 105 BAW 100 MHz x 100 SAW 500 MHz x 20 106

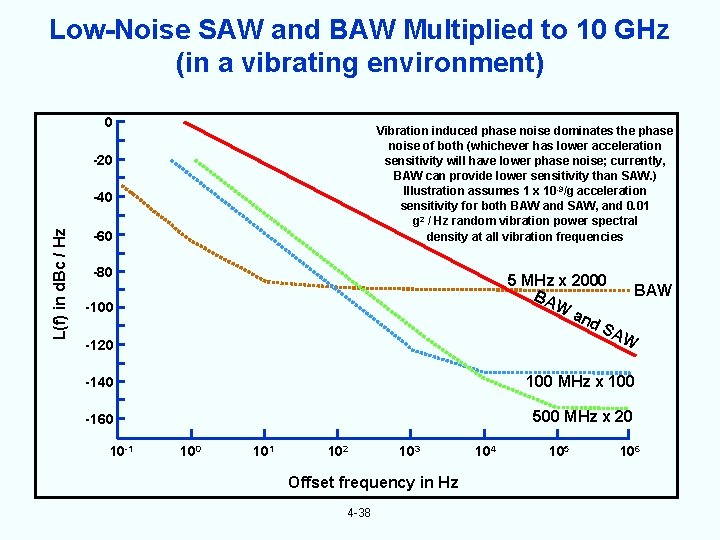
Low-Noise SAW and BAW Multiplied to 10 GHz (in a vibrating environment) 0 Vibration induced phase noise dominates the phase noise of both (whichever has lower acceleration sensitivity will have lower phase noise; currently, BAW can provide lower sensitivity than SAW. ) Illustration assumes 1 x 10 -9/g acceleration sensitivity for both BAW and SAW, and 0. 01 g 2 / Hz random vibration power spectral density at all vibration frequencies -20 L(f) in d. Bc / Hz -40 -60 -80 5 MHz x 2000 BAW BA W an d. S AW -100 -120 -140 100 MHz x 100 -160 500 MHz x 20 10 -1 100 101 102 103 Offset frequency in Hz 4 -38 104 105 106

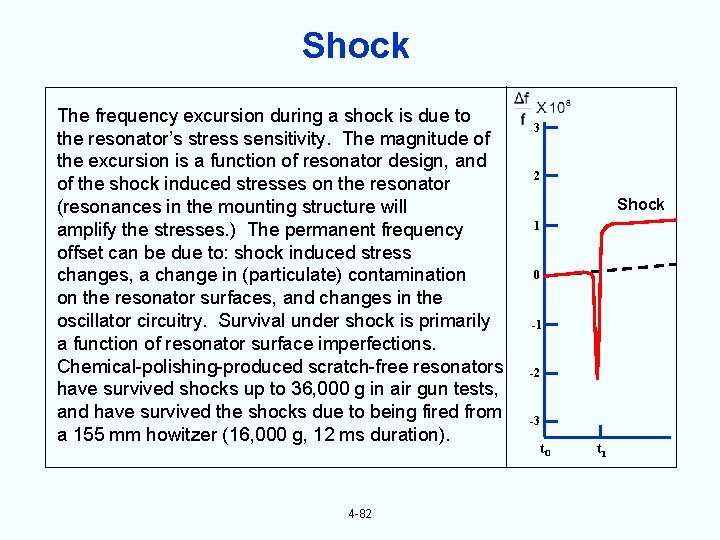
Shock The frequency excursion during a shock is due to the resonator’s stress sensitivity. The magnitude of the excursion is a function of resonator design, and of the shock induced stresses on the resonator (resonances in the mounting structure will amplify the stresses. ) The permanent frequency offset can be due to: shock induced stress changes, a change in (particulate) contamination on the resonator surfaces, and changes in the oscillator circuitry. Survival under shock is primarily a function of resonator surface imperfections. Chemical-polishing-produced scratch-free resonators have survived shocks up to 36, 000 g in air gun tests, and have survived the shocks due to being fired from a 155 mm howitzer (16, 000 g, 12 ms duration). 4 -82 3 2 Shock 1 0 -1 -2 -3 t. O t 1

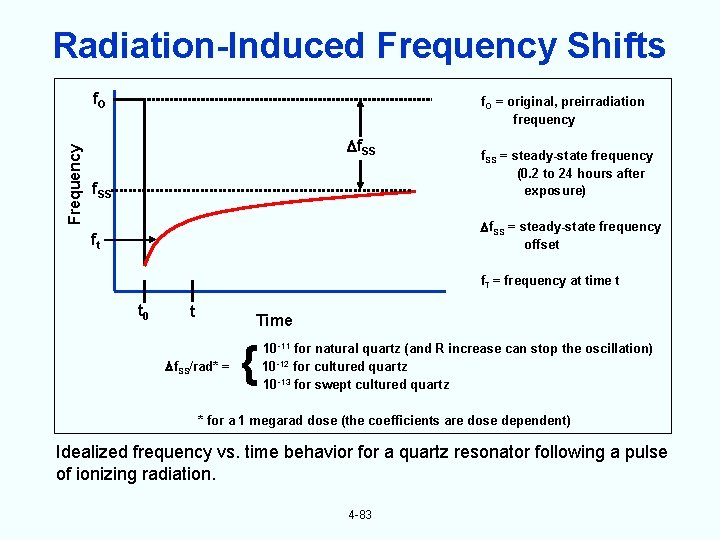
Radiation-Induced Frequency Shifts Frequency f. O = original, preirradiation frequency f. SS = steady-state frequency (0. 2 to 24 hours after exposure) ft f. SS = steady-state frequency offset f. T = frequency at time t t 0 t Time f. SS/rad* = { 10 -11 for natural quartz (and R increase can stop the oscillation) 10 -12 for cultured quartz 10 -13 for swept cultured quartz * for a 1 megarad dose (the coefficients are dose dependent) Idealized frequency vs. time behavior for a quartz resonator following a pulse of ionizing radiation. 4 -83

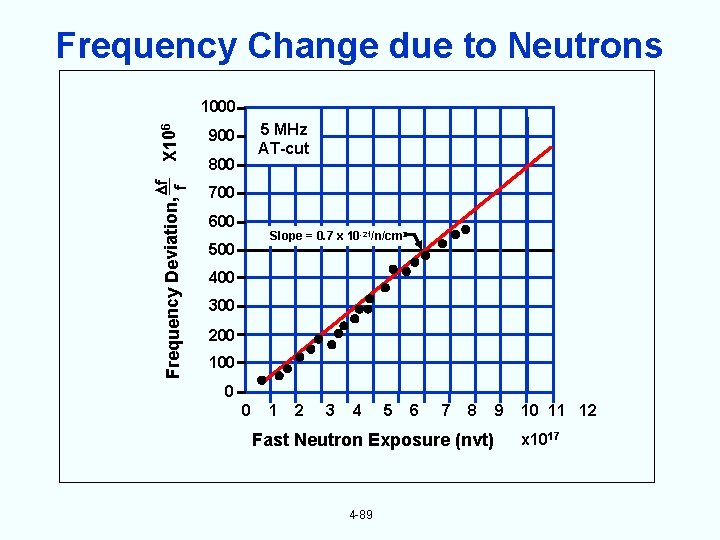
Frequency Change due to Neutrons Frequency Deviation, f f X 106 1000 5 MHz AT-cut 900 800 700 600 Slope = 0. 7 x 10 -21/n/cm 2 500 400 300 200 100 0 0 1 2 3 4 5 6 7 8 Fast Neutron Exposure (nvt) 4 -89 9 10 11 12 x 1017

Neutron Damage (1) (2) (3) (4) A fast neutron can displace about 50 to 100 atoms before it comes to rest. Most of the damage is done by the recoiling atoms. Net result is that each neutron cause numerous vacancies and interstitials. 4 -90

Other Effects on Stability Electric field - affects doubly-rotated resonators; e. g. , a voltage on the electrodes of a 5 MHz fundamental mode SC-cut resonator results in a f/f = 7 x 10 -9 per volt. The voltage can also cause sweeping, which can affect the frequency (of all cuts), even at normal operating temperatures. Magnetic field - quartz is diamagnetic, however, magnetic fields can induce Eddy currents, and will affect magnetic materials in the resonator package and the oscillator circuitry. Induced ac voltages can affect varactors, AGC circuits and power supplies. Typical frequency change of a "good" quartz oscillator is <<10 -10 per gauss. Ambient pressure (altitude) - deformation of resonator and oscillator packages, and change in heat transfer conditions affect the frequency. Humidity - can affect the oscillator circuitry, and the oscillator's thermal properties, e. g. , moisture absorbed by organics can affect dielectric constants. Power supply voltage, and load impedance - affect the oscillator circuitry, and indirectly, the resonator's drive level and load reactance. A change in load impedance changes the amplitude or phase of the signal reflected into the oscillator loop, which changes the phase (and frequency) of the oscillation. The effects can be minimized by using a (low noise) voltage regulator and buffer amplifier. Gas permeation - stability can be affected by excessive levels of atmospheric hydrogen and helium diffusing into "hermetically sealed" metal and glass enclosures (e. g. , hydrogen diffusion through nickel resonator enclosures, and helium diffusion through glass Rb standard bulbs). 4 -94

Interactions Among Influences In attempting to measure the effect of a single influence, one often encounters interfering influences, the presence of which may or may not be obvious. Short term stability Interfering Influence T due to oven T (i. e. , thermistor) aging drive level due to osc. circuit aging Vibration sensitivity Induced voltages due to magnetic fields 2 -g tipover sensitivity T due to convection inside oven Resonator f vs. T (static) Thermal transient effect, humidity T-coefficient of load reactances Radiation sensitivity T, thermal transient effect, aging Measurement Resonator aging 4 -95

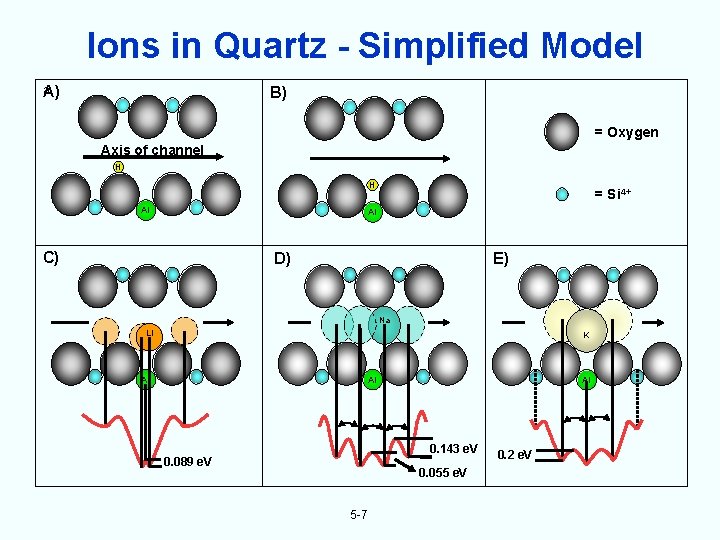
Ions in Quartz - Simplified Model a A) B) = Oxygen Axis of channel H H Al = Si 4+ Al C) D) E) Na Li K Al Al Al 0. 143 e. V 0. 089 e. V 0. 055 e. V 5 -7 0. 2 e. V

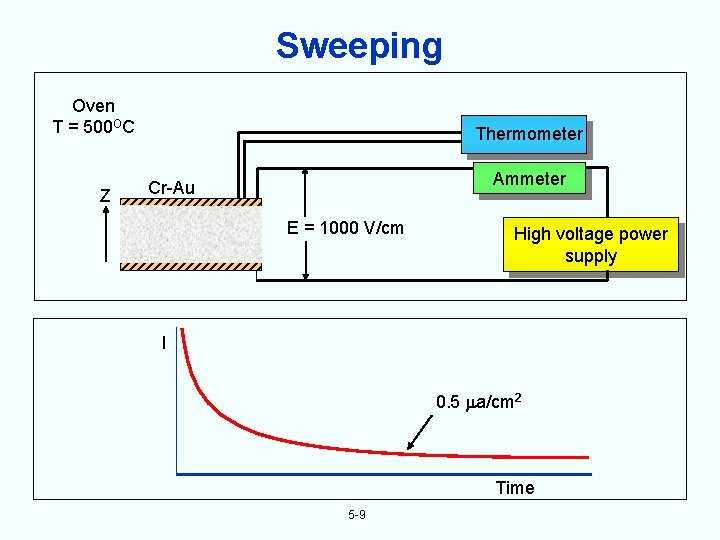
Sweeping Oven T = 500 OC Z Thermometer Ammeter Cr-Au Quartz bar E = 1000 V/cm High voltage power supply I 0. 5 a/cm 2 Time 5 -9

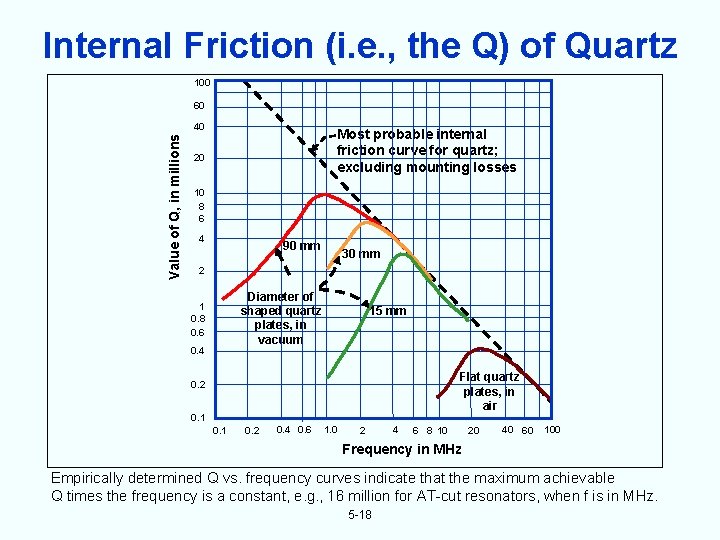
Internal Friction (i. e. , the Q) of Quartz 100 60 Value of Q, in millions 40 Most probable internal friction curve for quartz; excluding mounting losses 20 10 8 6 4 90 mm 30 mm 2 Diameter of shaped quartz plates, in vacuum 1 0. 8 0. 6 0. 4 15 mm Flat quartz plates, in air 0. 2 0. 1 0. 2 0. 4 0. 6 1. 0 2 4 6 8 10 20 40 60 100 Frequency in MHz Empirically determined Q vs. frequency curves indicate that the maximum achievable Q times the frequency is a constant, e. g. , 16 million for AT-cut resonators, when f is in MHz. 5 -18

Langasite and Its Isomorphs La 3 Ga 5 Si. O 14 Langasite (LGS) La 3 Ga 5. 5 Nb 0. 5 O 14 Langanite (LGN) La 3 Ga 5. 5 Ta 0. 5 O 14 Langatate (LGT) • Lower acoustic attenuation than quartz (higher Qf than AT- or SC-cut quartz) • No phase transition (melts at ~1, 400 o. C vs. phase transition at 573 o. C for quartz) • Higher piezoelectric coupling than quartz • Thicker than quartz at the same frequency • Temperature-compensated 5 -19

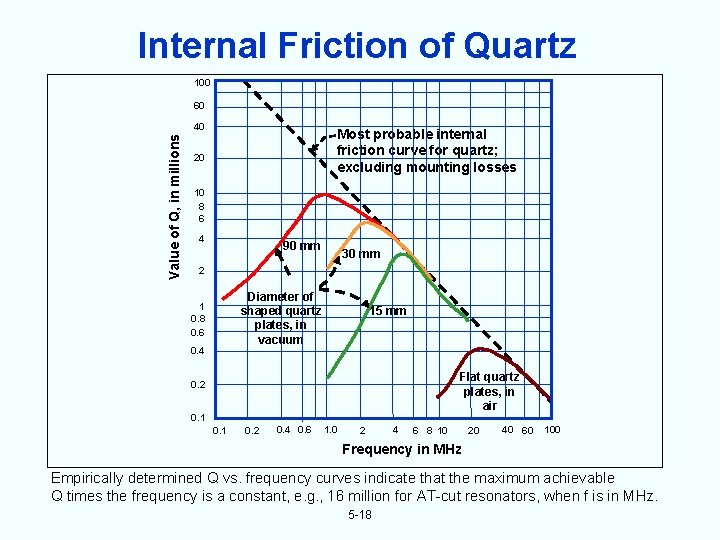
Internal Friction of Quartz 100 60 Value of Q, in millions 40 Most probable internal friction curve for quartz; excluding mounting losses 20 10 8 6 4 90 mm 30 mm 2 Diameter of shaped quartz plates, in vacuum 1 0. 8 0. 6 0. 4 15 mm Flat quartz plates, in air 0. 2 0. 1 0. 2 0. 4 0. 6 1. 0 2 4 6 8 10 20 40 60 100 Frequency in MHz Empirically determined Q vs. frequency curves indicate that the maximum achievable Q times the frequency is a constant, e. g. , 16 million for AT-cut resonators, when f is in MHz. 5 -18

Langasite and Its Isomorphs La 3 Ga 5 Si. O 14 Langasite (LGS) La 3 Ga 5. 5 Nb 0. 5 O 14 Langanite (LGN) La 3 Ga 5. 5 Ta 0. 5 O 14 Langatate (LGT) • Lower acoustic attenuation than quartz (higher Qf than AT- or SC-cut quartz) • No phase transition (melts at ~1, 400 o. C vs. phase transition at 573 o. C for quartz) • Higher piezoelectric coupling than quartz • Thicker than quartz at the same frequency • Temperature-compensated 5 -19

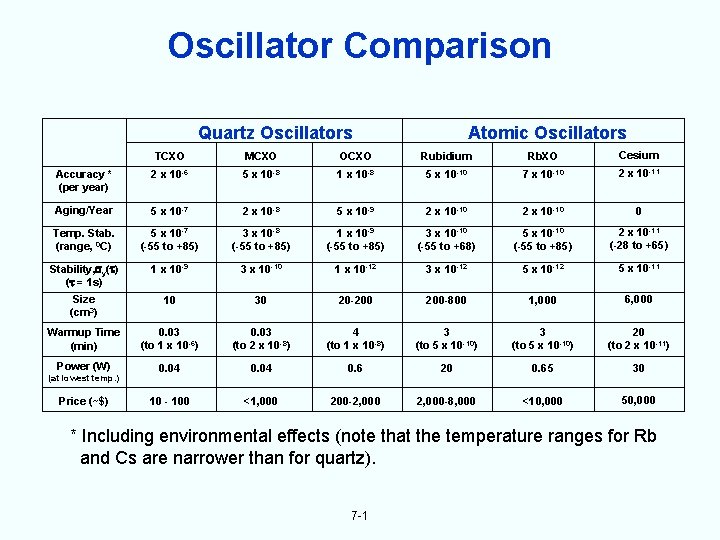
Oscillator Comparison Quartz Oscillators Atomic Oscillators TCXO MCXO OCXO Rubidium Rb. XO Cesium Accuracy * (per year) 2 x 10 -6 5 x 10 -8 1 x 10 -8 5 x 10 -10 7 x 10 -10 2 x 10 -11 Aging/Year 5 x 10 -7 2 x 10 -8 5 x 10 -9 2 x 10 -10 0 Temp. Stab. (range, 0 C) 5 x 10 -7 (-55 to +85) 3 x 10 -8 (-55 to +85) 1 x 10 -9 (-55 to +85) 3 x 10 -10 (-55 to +68) 5 x 10 -10 (-55 to +85) 2 x 10 -11 (-28 to +65) Stability, y( ) ( = 1 s) 1 x 10 -9 3 x 10 -10 1 x 10 -12 3 x 10 -12 5 x 10 -11 Size (cm 3) 10 30 20 -200 200 -800 1, 000 6, 000 Warmup Time (min) 0. 03 (to 1 x 10 -6) 0. 03 (to 2 x 10 -8) 4 (to 1 x 10 -8) 3 (to 5 x 10 -10) 20 (to 2 x 10 -11) Power (W) 0. 04 0. 6 20 0. 65 30 10 - 100 <1, 000 200 -2, 000 -8, 000 <10, 000 50, 000 (at lowest temp. ) Price (~$) * Including environmental effects (note that the temperature ranges for Rb and Cs are narrower than for quartz). 7 -1

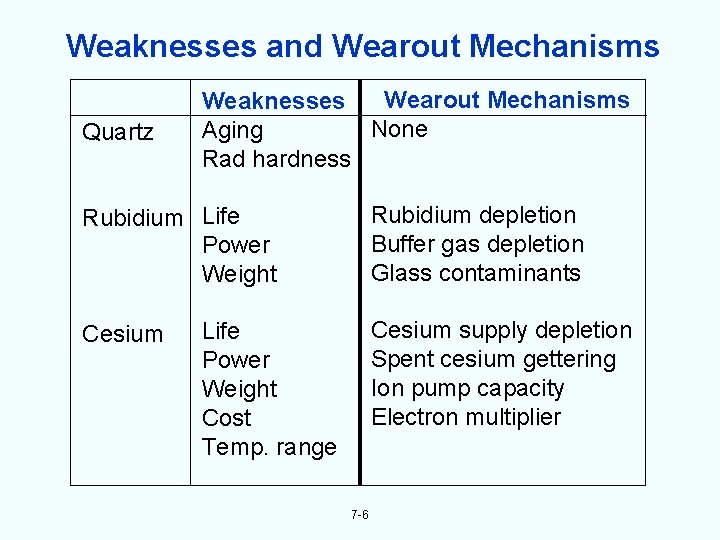
Weaknesses and Wearout Mechanisms Quartz Weaknesses Wearout Mechanisms None Aging Rad hardness Rubidium depletion Buffer gas depletion Glass contaminants Rubidium Life Power Weight Cesium supply depletion Spent cesium gettering Ion pump capacity Electron multiplier Life Power Weight Cost Temp. range 7 -6

Why Do Crystal Oscillators Fail? Crystal oscillators have no inherent failure mechanisms. Some have operated for decades without failure. Oscillators do fail (go out of spec. ) occasionally for reasons such as: Poor workmanship & quality control - e. g. , wires come loose at poor quality solder joints, leaks into the enclosure, and random failure of components Frequency ages to outside the calibration range due to high aging plus insufficient tuning range TCXO frequency vs. temperature characteristic degrades due to aging and the “trim effect”. OCXO frequency vs. temperature characteristic degrades due to shift of oven set point. Oscillation stops, or frequency shifts out of range or becomes noisy at certain temperatures, due to activity dips Oscillation stops or frequency shifts out of range when exposed to ionizing radiation - due to use of unswept quartz or poor choice of circuit components Oscillator noise exceeds specifications due to vibration induced noise Crystal breaks under shock due to insufficient surface finish 7 -8

Oscillator Selection Considerations Frequency accuracy or reproducibility requirement Recalibration interval Environmental extremes Power availability - must it operate from batteries? Allowable warmup time Short term stability (phase noise) requirements Size and weight constraints Cost to be minimized - acquisition or life cycle cost 7 -9

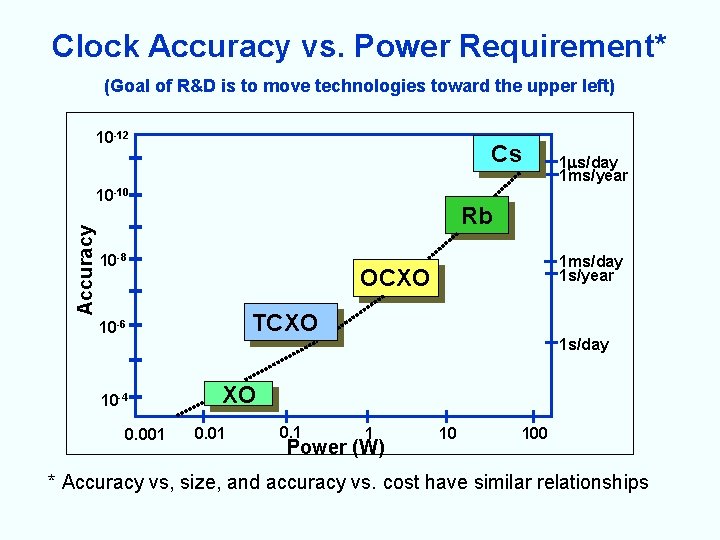
Clock Accuracy vs. Power Requirement* (Goal of R&D is to move technologies toward the upper left) 10 -12 Cs Accuracy 10 -10 Rb 10 -8 0. 001 1 ms/day 1 s/year OCXO TCXO 10 -6 10 -4 1 s/day 1 ms/year 1 s/day XO 0. 01 0. 1 1 Power (W) 10 100 * Accuracy vs, size, and accuracy vs. cost have similar relationships

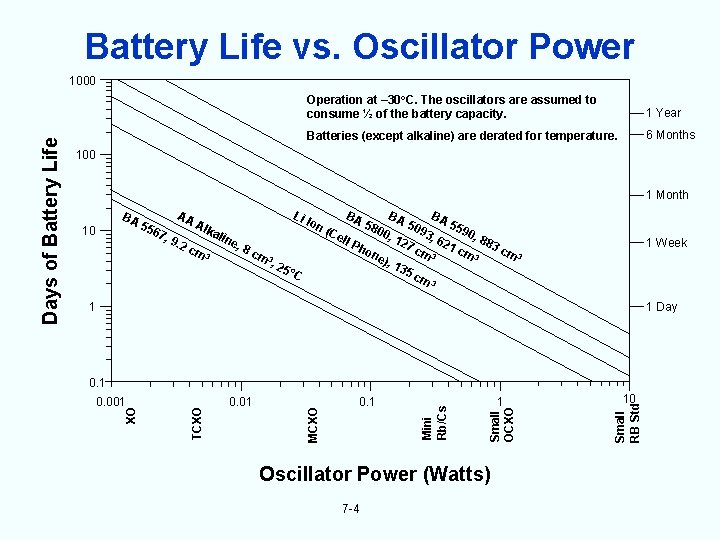
Battery Life vs. Oscillator Power Operation at – 30 o. C. The oscillators are assumed to consume ½ of the battery capacity. 1 Year Batteries (except alkaline) are derated for temperature. 6 Months 100 1 Month BA 10 55 67 , 9 AA. 2 Alk cm 3 ali n Li Io e, BA n( 8 c m 3 , 2 Ce ll P 58 ho 00 BA , 1 ne ), 5°C 50 27 13 93 BA , 6 cm 3 55 21 90 , 8 8 cm 3 3 cm 3 1 Week 5 c m 3 1 Day 1 Oscillator Power (Watts) 7 -4 10 Small RB Std 1 Small OCXO 0. 1 Mini Rb/Cs 0. 01 MCXO 0. 001 TCXO 0. 1 XO Days of Battery Life 1000

Crystal Oscillator Specification: MIL-PRF-55310 D 15 March 1998 -----------SUPERSEDING MIL-0 -55310 C 15 Mar 1994 PERFORMANCE SPECIFICATION OSCILLATOR, CRYSTAL CONTROLLED GENERAL SPECIFICATION FOR This specification is approved for use by all Departments and Agencies of the Department of Defense. 1. SCOPE 1. 1 Statement of scope. This specification covers the general requirements for quartz crystal oscillators used in electronic equipment. -----------------Full text version is available via a link from <http: \www. ieee. org/uffc/fc> 7 -10

IEEE Frequency Control Website A huge amount of frequency control information can be found at www. ieee-uffc. org/fc Available at this website are >100 K pages of information, including the full text of all the papers ever published in the Proceedings of the Frequency Control Symposium, i. e. , since 1956, reference and tutorial information, ten complete books, historical information, and links to other web sites, including a directory of company web sites. Some of the information is openly available, and some is available to IEEE UFFC Society members only. 10 -6

IEEE Electronic Library The IEEE/IEE Electronic Library (IEL) contains more than one million documents; almost a third of the world's electrical engineering and computer science literature. It features high-quality content from the Institute of Electrical and Electronics Engineers (IEEE) and the Institution of Electrical Engineers (IEE). Full-text access is provided to journals, magazines, transactions and conference proceedings as well as active IEEE standards. IEL includes robust search tools powered by the intuitive IEEE Xplore interface. www. ieee. org/ieeexplore 10 -7