Quapprendon dans ce chapitre Questce que la classification

Qu’apprend-on dans ce chapitre • Qu’est-ce que la classification pour une image ; • Des exemples de classification ‘simple’ : • Non paramétrique : les k-PPV ; • Non supervisée : seuillage de Otsu, les c-moyennes ; • Qu’est-ce qu’une classification bayésienne et comment se formule le critère Maximum A Posteriori ; • Qu’est-ce que la classification SVM et dans quel cas estelle particulièrement intéressante ;

Classification : objectifs • Mettre en évidence les similarités/ dissimilarités entre les ‘objets’ (e. g. pixels) • Obtenir une représentation simplifiée (mais pertinente) des données originales Mettre sous un même label les objets ou pixels similaires Définitions préalables • Espace des caractéristiques d ( s S, ys d) • Espace de décision = ensemble des classes W ( s S, xs W), W = {wi, i [1, c] } • Règle de décision ( = d(ys) ) • Critère de performance Passer de l’espace des caractéristiques à celui des classes → règle : supervisée / non supervisée, paramétrique / non paramétrique, probabiliste / syntaxique / autre, avec rejet / sans rejet

Ex. de classification non paramétrique Possibilité de modélisation de loi complexes, de forme non nécessairement paramétrique (ex. en 2 D disque et couronne) • Classification k-ppv (plus proches voisins) On dispose d’un ensemble (de ‘référence’) d’objets déjà labelisés Pour chaque objet y à classifier, on estime ses k ppv selon la Euclidienne, métrique de l’espace des caractéristiques, et on lui affecte le Mahanolobis label majoritaire parmi ses k ppv … Possibilité d’introduire un rejet (soit en distance, soit en ambiguïté) Très sensible à l’ensemble de référence • Exemples : k-ppv (/24) 1 -ppv 3 -ppv 5 -ppv

Connaissance des caractéristiques des classes • Cas supervisé – Connaissance a priori des caractéristiques des classes – Apprentissage à partir d’objets déjà étiquetés (cas de données ‘complètes’) • Cas non supervisé Définition d’un critère, ex. : - minimisation de la probabilité d’erreur - minimisation de l’inertie intra-classe maximisation de l’inertie inter-classes Définition d’un algorithme d’optimisation

Equivalence minimisation de la dispersion intraclasse / maximisation de la dispersion inter-classes

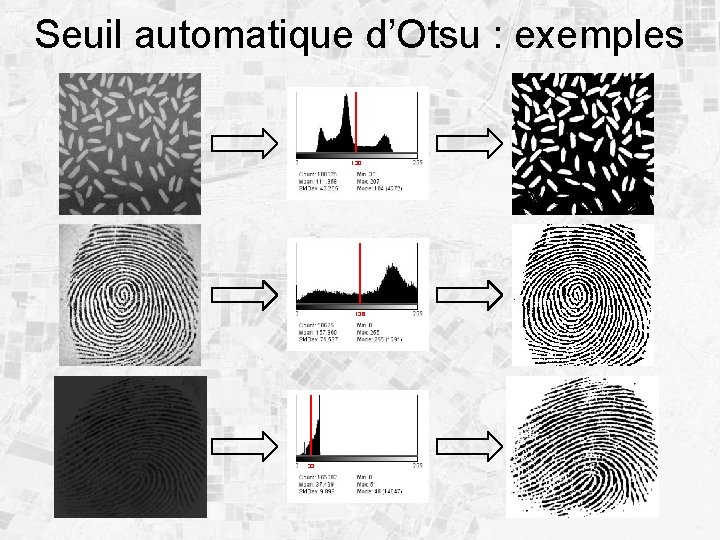
Application : seuil automatique d’Otsu Algorithme • Calcul de l’histogramme de l’image • Initialisations: m 1=min(I), |C 1|=0, m 2=<I>, |C 2|=N, s=0, Dmax=0 • Pour chaque bin j de l’histogramme centré autour de xj et ayant nj pixels • • • m 1 (|C 1|m 1+nj. xj)/(|C 1|+nj) ; |C 1|+nj ; m 2 (|C 2|m 2 -nj. xj)/(|C 2|-nj) ; |C 2|-nj ; si |C 1||C 2|(m 1 - m 2)2>Dmax, alors Dmax= |C 1||C 2|(m 1 - m 2)2 et s=xj

Seuil automatique d’Otsu : exemples 130 136 33

Algorithme des c-moyennes (cas non sup. ) • Initialisation (itération t=0) : choix des centres initiaux (e. g. aléatoirement, répartis, échantillonnés) • Répéter jusqu’à vérification du critère d’arrêt : – t++ – Pour chaque pixel, labelisation par la plus proche classe – Nombre de changements : – Mise à jour des centres par minimisation de l’erreur quadratique : – Estimation du critère d’arrêt (e. g. test sur nb_ch(t) ) c=5 c=4 c=3 (s=30) c=2 Exemple : Remarques : Nombre de classes a priori Dépendance à l’initialisation

Variantes K-moyennes • ISODATA – Regroupement ou division de classes nouveaux paramètres : q. N=nbre min objets par classe, q. S seuil de division (division de la classe i si : maxj [1, d]sij > q. S et nbre objets de la classe > 2 q. N+1 et Iintra(i) > Iintra ), q. C seuil de regroupement (regroupement des classes i et j si : dist(mi, mj) q. C), nbre max itérations • Nuées dynamiques – Remplacement de la mesure de ‘distance’ par une mesure de ‘dissemblance’ dis(ys, wi) minimiser classe i représentée par son ‘noyau’, e. g. centre ( K-moyennes), plusieurs ‘échantillons’ de référence zl l [1, p] (dis(. , . ) = moyenne des distances de l’objet aux zl)

Probabilités et mesure de l’information • Probabilités fréquencistes / subjectivistes Physique stat. : répétition de phénomènes dans des ‘longues’ séquences probabilité = passage à la limite d’une fréquence ≠ Modèle de connaissance a priori : degré de confiance relatif à un état de connaissance probabilité = traduction numérique d’un état de connaissance • Remarque : Quantité d’information et probabilités I = -log 2(pi) I ≥ 0, information d’autant plus importante que évènement inattendu (de faible probabilité)

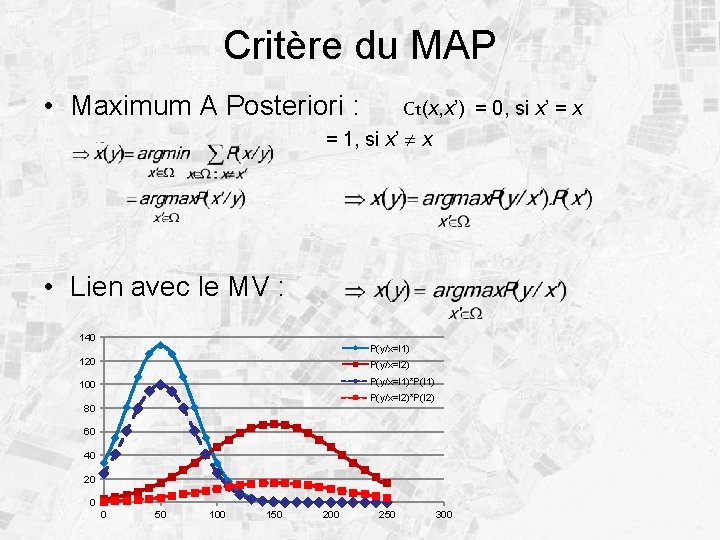
Théorie bayésienne de la décision • La théorie de la décision bayésienne repose sur la minimisation du ‘risque’ • Soit Ct(x, x’) le coût associé à la décision de x’ alors que la réalisation de X était x • La performance de l’estimateur x’ est mesurée par le P(x’/x, y)=P(x’/y) car risque de Bayes E[Ct(x, x’)] = décision selon y seul Coût marginal (conditionnel à y) à minimiser Or x’P(x’/y)=1 et x’, P(x’/y)≥ 0, La règle qui minimise le coût moyen est donc celle telle que P(x’/y)=1 si et seulement si x. P(x/y)Ct(x, x’) minimale

Exemple • Détection d’un véhicule dangereux (V) • Décider V si et seulement si Cas où a>b, on va décider plus facilement V que V en raison du coût plus fort d’une décision erronée en faveur de V que de V

Critère du MAP • Maximum A Posteriori : Ct(x, x’) = 0, si x’ = x = 1, si x’ x • Lien avec le MV : 140 P(y/x=l 1) 120 P(y/x=l 2) 100 P(y/x=l 1)*P(l 1) P(y/x=l 2)*P(l 2) 80 60 40 20 0 0 50 100 150 200 250 300

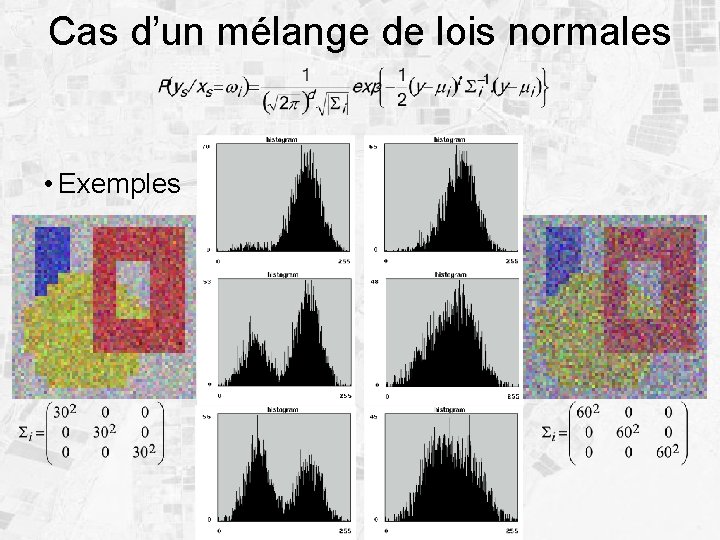
Cas d’un mélange de lois normales • Exemples

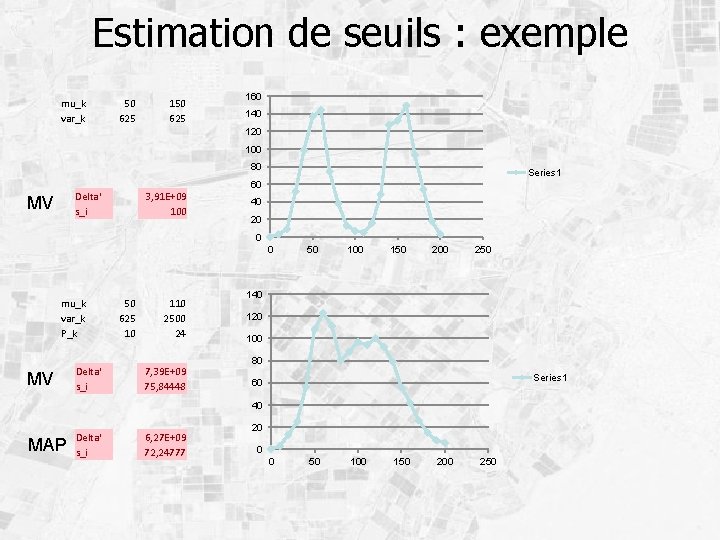
Estimation de seuils (cas supervisé) • Image = ensemble d’échantillons suivant une loi de distribution de paramètres déterminés par la classe ex. : distribution gaussienne • Cas 1 D (monocanal), si seuil de séparation des classes wi et wi+1, probabilité d’erreur associée : – Maximum de vraisemblance :

– Maximum de vraisemblance (suite) : – Maximum A Posteriori :

Estimation de seuils : exemple mu_k var_k 50 625 160 140 120 100 80 Delta' s_i MV 3, 91 E+09 100 Series 1 60 40 20 0 0 mu_k var_k P_k MV Delta' s_i 50 625 10 110 2500 24 7, 39 E+09 75, 84448 50 100 150 200 250 140 120 100 80 Series 1 60 40 MAP Delta' s_i 6, 27 E+09 72, 24777 20 0 0 50 100 150 200 250

Lien c-moyennes / théorie bayésienne • Maximum de vraisemblance sur des lois de paramètres qi (e. g. qi=(mi, i)) inconnus : en effet : • Cas d’échantillons indépendants : max. de la logvraisemblance en effet : d’où : (*) or : d’où (*) • Cas gaussien, i connus, mi inconnus résolution itérative c-moyennes : i=Id i [1, c] et P(wi | ys, q) = 1 si wi = xs, = 0 sinon

Classification SVM (Séparateurs à Vastes Marges) (Vapnik, 1995) • Exemple de classification à base d’apprentissage Supervisé / Semi-supervisé • Hyp. : 1 classifieur linéaire dans un espace approprié utilisation de fonctions à noyau pour projetter les données dans cet espace • Exemple simplissime (cas binaire & linéairement séparable) Critère d’optimalité maximisation de la marge distance entre hyperplan et ens. des échantillons Marge Hyperplan séparateur Vecteurs de support Ensemble d’apprentissage {(y 1, x 1), (y 2, x 2), …, {(y. N, x. N)} équation de l’hyperplan

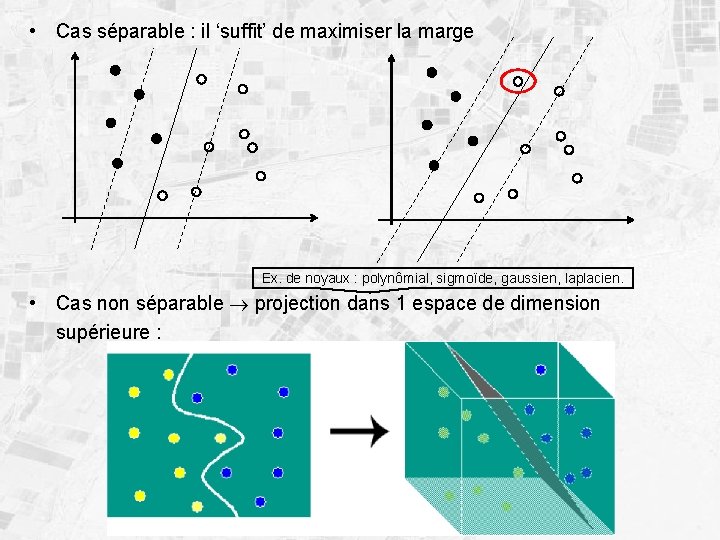
• Cas séparable : il ‘suffit’ de maximiser la marge Ex. de noyaux : polynômial, sigmoïde, gaussien, laplacien. • Cas non séparable projection dans 1 espace de dimension supérieure :

Calcul de l’hyperplan (cas linéaire, 2 classes) xi {-1, 1} • Éq. de l’hyperplan séparateur : h(y) = w. Ty + w 0 = 0 • Cas séparable linéairement : {(y 1, x 1), (y 2, x 2), …, {(y. N, x. N)} échantillons d’apprentissage Ty + w = 0, la distance d’un point M est un hyperplan d’éq. • Pour Problème sous sawforme 0 ‘primale’ marge = On choisit que min(w. Ty + w 0 ) = 1 (i. e. pour les vecteurs de support) Maximiser 1/||w|| (i. e. la marge) minimiser sous contrainte minimiser lagrangien :

Calcul de l’hyperplan (cas linéaire, 2 classes) |w. Ty + w 0| 1 • Problème sous sa forme ‘duale’ en annulant les dérivées partielles du lagrangien / w 0 et w : À injecter dans l’eq. du lagrangien Soluble par programmation quadratique Ne fait intervenir que les vecteurs de support

SVM Cas non linéaire • Transformation non linéaire f Nécessaire de connaître uniquement le produit scalaire • Exemples de noyaux polynômial gaussien Fonction à noyau

Utilisation des SVM pour la classif. d’image • Principalement cas de données de grande dimension Niveau pixel caractéristiques multi-échelles caractéristiques spectrales Niveau objet caractéristiques de forme caractéristiques de texture Niveau image À comparer avec k-ppv, & réseaux de neurones En entrée de la classif. : 1 image des données + 1 segmentation labelisat° des segments Classification de l’image, e. g. en terme de type de scène caractéristiques en termes de pixels d’intérêt • Difficulté principale : choix des caractéristiques en entrée, du noyau de la stratégie pour passer en multi-classes (1 contre 1, 1 contre tous) SVM boite ‘noire’ efficace mais interprétation a posteriori limitée

Utilisation des SVM pour la classif. d’image: Cas multi-classes • k classes, k 3 : Entrainement et exécution de SVM binaires (2 classes) puis combinaison des résultats obtenus par ces SVMs cas de SVM binaires 1 versus 1 : vote majoritaire sur les décisions (si k classes, k-1 SVMs 1 vs 1 impliquent la ‘bonne classe’ et les autres non la ‘bonne’ classe recueille 2 fois + de votes que les autres classes) cas de SVM binaires 1 versus all : décision en faveur du score le plus élevé obtenu sur l’ensemble des SVM 1 vs. All stratégie nbre de classifieurs SVM temps de calcul Redondance (robustesse) 1 versus 1 Ck 2=k(k-1)/2 +++ 1 versus all k + ++

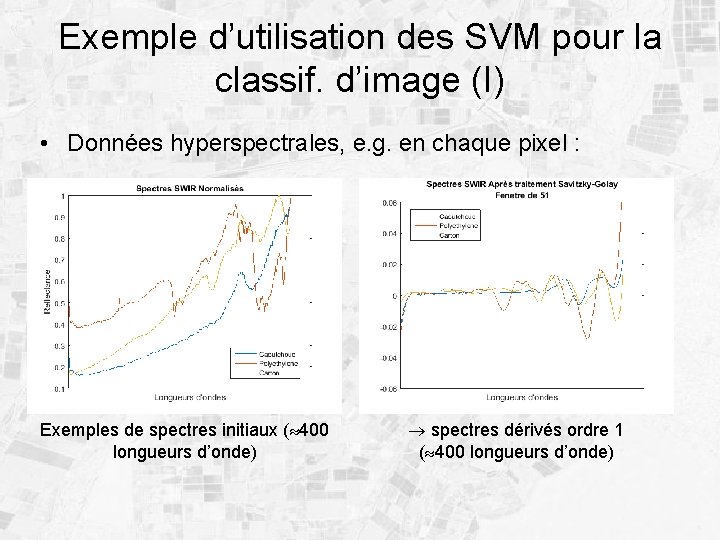
Exemple d’utilisation des SVM pour la classif. d’image (I) • Données hyperspectrales, e. g. en chaque pixel : Exemples de spectres initiaux ( 400 longueurs d’onde) spectres dérivés ordre 1 ( 400 longueurs d’onde)

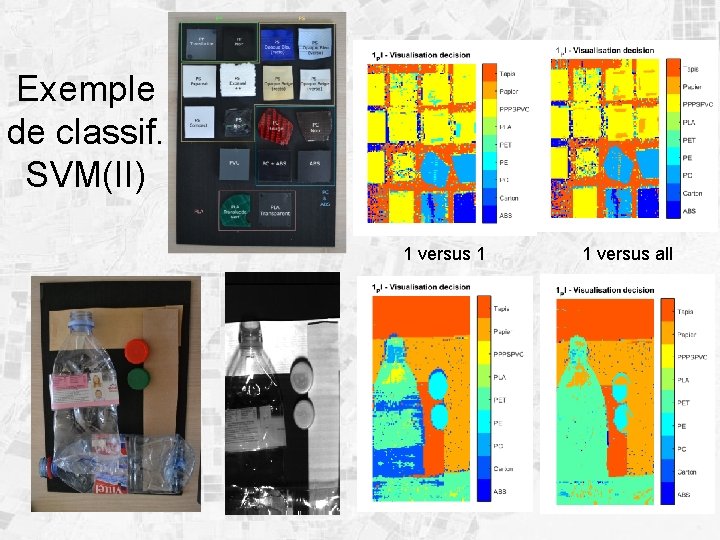
Exemple de classif. SVM(II) 1 versus 1 1 versus all

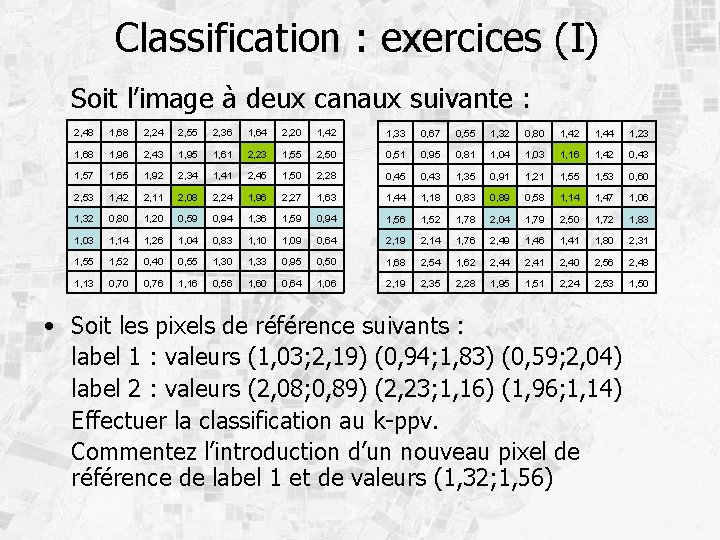
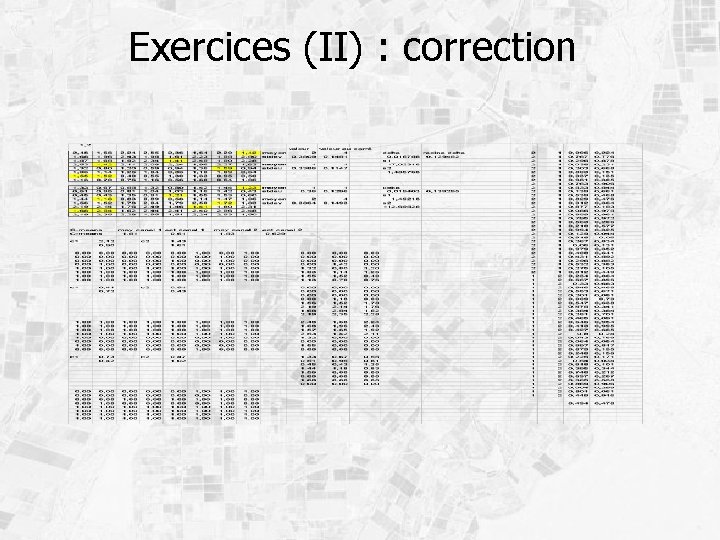
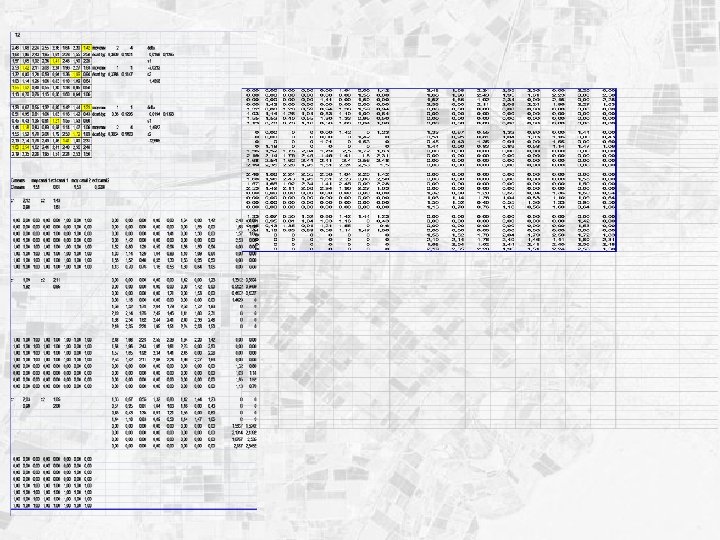
Classification : exercices (I) Soit l’image à deux canaux suivante : 2, 48 1, 68 2, 24 2, 55 2, 36 1, 64 2, 20 1, 42 1, 33 0, 67 0, 55 1, 32 0, 80 1, 42 1, 44 1, 23 1, 68 1, 96 2, 43 1, 95 1, 61 2, 23 1, 55 2, 50 0, 51 0, 95 0, 81 1, 04 1, 03 1, 16 1, 42 0, 43 1, 57 1, 65 1, 92 2, 34 1, 41 2, 45 1, 50 2, 28 0, 45 0, 43 1, 35 0, 91 1, 21 1, 55 1, 53 0, 60 2, 53 1, 42 2, 11 2, 08 2, 24 1, 96 2, 27 1, 63 1, 44 1, 18 0, 83 0, 89 0, 58 1, 14 1, 47 1, 06 1, 32 0, 80 1, 20 0, 59 0, 94 1, 36 1, 59 0, 94 1, 56 1, 52 1, 78 2, 04 1, 79 2, 50 1, 72 1, 83 1, 03 1, 14 1, 26 1, 04 0, 83 1, 10 1, 09 0, 64 2, 19 2, 14 1, 76 2, 49 1, 46 1, 41 1, 80 2, 31 1, 55 1, 52 0, 40 0, 55 1, 30 1, 33 0, 95 0, 50 1, 68 2, 54 1, 62 2, 44 2, 41 2, 40 2, 56 2, 48 1, 13 0, 70 0, 76 1, 16 0, 56 1, 60 0, 64 1, 06 2, 19 2, 35 2, 28 1, 95 1, 51 2, 24 2, 53 1, 50 • Soit les pixels de référence suivants : label 1 : valeurs (1, 03; 2, 19) (0, 94; 1, 83) (0, 59; 2, 04) label 2 : valeurs (2, 08; 0, 89) (2, 23; 1, 16) (1, 96; 1, 14) Effectuer la classification au k-ppv. Commentez l’introduction d’un nouveau pixel de référence de label 1 et de valeurs (1, 32; 1, 56)

Classification : exercices (II) Sur l’image à deux canaux précédente : • Déterminer les seuils de décision pour chacun des canaux si l’on suppose 2 classes gaussiennes de caractéristiques respectives : canal 1 : (m 1, s 1)=(2. 0, 0. 38), (m 2, s 2)=(1. 0, 0. 34) canal 2 : (m 1, s 1)=(1. 0, 0. 36), (m 2, s 2)=(2. 0, 0. 39) Effectuer la classification par seuillage. • Effectuer la classification c-means pour c=2. Comparer avec les résultats précédents. Comparer avec la classification c-means pour c=3.

Exercices (II) : correction