Quantum Zeno Effect Current Research and Future Applications

Quantum Zeno Effect : Current Research and Future Applications - Raghuram Kamath

Theme of the Presentation: • What is QZE? • First QZE experiment • Current Research / Future Applications

Part 1 What is the Quantum Zeno effect? § Quantum Zeno effect is defined as the suppression of the temporal evolution of an unstable system under continuous measurements from any observing party, during a defined period of time. § The dynamic evolution of a quantum system is said to be halted, due to the collapse of the wave function of the system, provided the measurements done by the observer are frequent enough, and thus continuous, in principal. § In essence, an unstable particle when observed continuously whether it has decayed or not will never be found to decay. “QZE ‘freezes’ the evolution of an undecayed system, and through this we can exploit several properties to our advantage, as we will see later in the presentation”

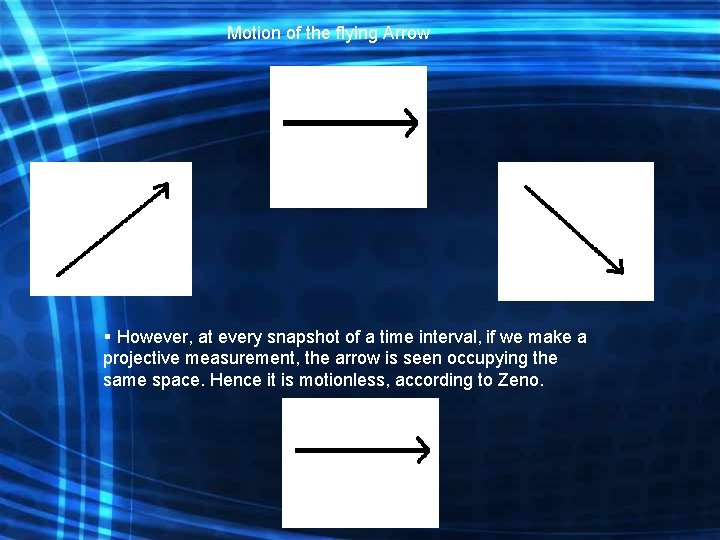
The Original Zeno’s Paradox § Zeno of Elia, the great Greek philosopher proposed several paradoxes out of which the paradox of the flying arrow or the Fletcher’s paradox is the most famous. § Zeno posits the paradox in the following way: ‘ If the motion is to occur, an object must change the position it occupies. If everything when it occupies an equal space at every instant is at rest, and that a body when in locomotion occupies such a space, then the flying arrow is motionless’ § At every instant of time, the arrow lies in the same space, and hence Zeno considered it to be motionless, or rather he remarked ‘Motion is an Illusion’

Motion of the flying Arrow § However, at every snapshot of a time interval, if we make a projective measurement, the arrow is seen occupying the same space. Hence it is motionless, according to Zeno.

The definition of the QZE is that ‘ When an unstable particle is measured to check whether it has evolved or not frequently, we inhibit its evolution and it does not evolve’. While writing the original paper in 1976 on QZE, B Misra and G Sudarshan, found this peculiar and drew a parallel to the flying arrow paradox, where the possibility of motion to the arrow is denied. And hence the name: ‘Quantum Zeno Effect’

A Simple Intuitive Analogy § Imagine person A and person B are in a room. Person A has just arrived home and is tired. He wants to take a nap. He intimates the same to person B and tries to sleep. § After some time, say half a minute (assuming it takes more than half a minute to go to sleep), Person B asks Person A whether he is asleep. The obvious reply from A is ‘No, I am not asleep’ and then he tries to sleep again. § Now again after half a minute, B asks A whether he is asleep, and the same thing happens again. Here by asking A whether he is asleep or no, B does not allow him to take a nap. § If the state of being ‘Sleepy’ is considered to be an unstable state and being ‘Asleep’ is the state which the system , here A, wants to evolve to, the frequent queries by B act as frequent measurements which ‘freezes’ the evolution.

Simple Mathematical Proof § Consider an unstable quantum state ׀ ɸ(0)> at the time instant t = 0. Also let ‘H’ be the Hamiltonian which describes the evolution of the system in the following way: ׀ ɸ(t)> = exp(-i. Ht) ׀ ɸ(0)> Where ׀ ɸ(t)> is the evolved state at the instant ‘t’ If we measure the state after a small time interval δt, the survival probability of ׀ ɸ(0)> can be measured by: P = {<ɸ(0) ׀ ɸ(δt)>} which equals P = exp(-i. Hδt) <ɸ(0) ׀ ɸ(0)> § Taking the Taylors expansion of the exponential term we get, P = 1 + (-i. Hδt)2 / 2 + …. .

Consider, the (-i. Hδt) term: We can approximate δt to be very small, and thus we can consider the above term to be approximately equal to 0. Consider the terms equal to or higher than order of 3. i. e. (-i. Hδt)n )/ n ; n>2 If δt is sufficiently small, higher powers of the above term become very small, and thus can be effectively neglected. Thus the probability reduces to the following term after approximation: P = 1 – {(δt)2 * Ĥ 2 }/2 Where Ĥ 2 denotes the fluctuation in H. Therefore, if we perform N measurements during a fixed time interval Δt = N*δ(t), the final survival probability becomes P = 1 – {(Δt)2 * Ĥ 2 }/2 N 2

§When we increase N, such that N tends to infinity, or N → ∞, we find that, the probability of the survival of the state tends to 0, or P → 0. Thus as we goon increasing N, we decrease P and thus this concludes a simple proof of why, in principle, the state never decays and remains in the state ׀ ɸ(0)>. Note that when we mention N → ∞, we imply that we make the time duration between two successive measurements very small and thus can be considered as being continuous. A lot depends on the measuring apparatus when an experiment of the QZE is carried out, since it determines how short the time interval of measurement is i. e. δt , which in turn depends on the resolution of the device.

Part 2 The first QZE Experiment § It took 13 years since the seminal QZE paper by Misra and Sudarshan in 1976, for researchers to come out with the first verifiable experiment. § The first widely recognized QZE experiment was carried out successfully by Itano, Heinzen, Bollinger and Wineland in 1989, when they observed this effect in an rf transition between two 9 Be+ ground state hyperfine levels. § The experiment considered the three levels viz. Level 1, Level 2 and Level 3 of the 9 Be+ ground states. The point of interest was the induced transition from Level 1 to Level 2, and thus a 313 nm radiation was left on for about 5 sec to make sure all the 9 Be+ ions were at Level 1 and Level 2 was practically empty.

§ A 320. 7 Mhz field was turned on for abut 256 ms so that transitions from 1 to 2 could be induced in the hyperfine levels. Short pulses of light applied at the same time as the rf field recorded the measurements. Ions at one level scattered a few photons while in the other level, no photons were scattered and thus distinguishing between levels was possible and hence detection was carried out. The statistical probability of the transition occurring can be modeled in terms of the parameter ‘n’ as follows: p = 0. 5 * [1 – cosn(π/n)] where n is the number of measurement light pulses applied.

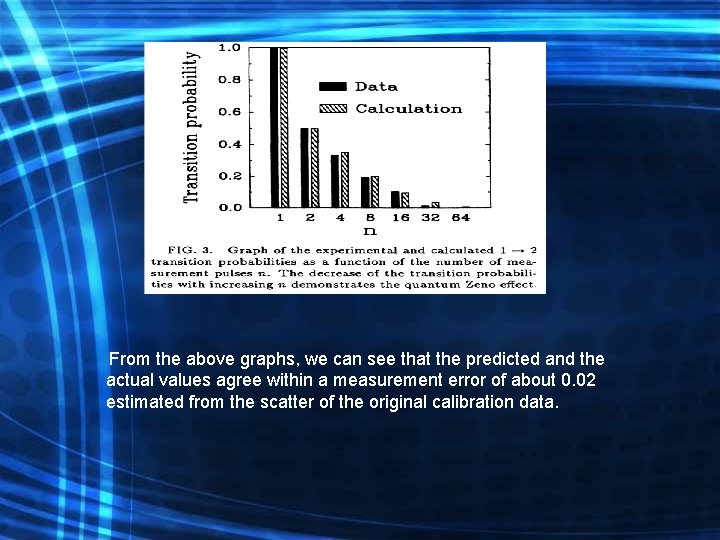
With the probability of transitions is p = 0. 5 * [1 – cosn(π/n)] , we get the following experimental results. As we can see, as we increase n or the number of times the measurements are made, we reduce the probability of transitions and hence demonstrate QZE.

From the above graphs, we can see that the predicted and the actual values agree within a measurement error of about 0. 02 estimated from the scatter of the original calibration data.

Part 3 Current Research / Future Applications § After the breakthrough experiment in 1990, a lot of research was kickstarted in this field. It was initially assumed that this is an effect which is a peculiar property, only realizable in the quantum world. § However this was later believed to be false, and several experiment sand proposals since then have been demonstrated which show that this effect can be possible in the classical realm too. § One of the most promising proposals was given this year in October by some prominent researchers namely Wang, Gu and Lin from the Chinese University of Hong Kong. They gave a proposal for observing the Classical Zeno effect in Optics.

§ Since there is no measurement in (a), the intensity of polarization beam for the y component evolves smoothly as a function of z. However in the second case (b), the resulted intensity is dramatically changed. In Fig. 1(b), we do a vertical-polarization measurement (along the y direction) after each Faraday medium, then the resulted intensity of the polarization beam for the y component becomes: I(z) =Io [cos 2(π/2 N)]i-1 cos 2{π/2 L[ z- (L/N)(i -1)]} Where Io is the initial intensity of light, before it is passed through the Faraday media and Where L is the total length of all the faraday media. § Also N is the total number of Faraday media with the same polarization rotation angle π/(2 N), and i denotes the ith Faraday medium at which the distance z is located.

Therefore, the intensity for the polarization light beam for the y component at the output end finally becomes: Iout = Io [cos 2{π/(2 N)}]N In this, as we increase N, we observe that as N→∞, the output intensity at the output end will be close to Io, which is the initial intensity that we started in. This in principle, is the Zeno effect.

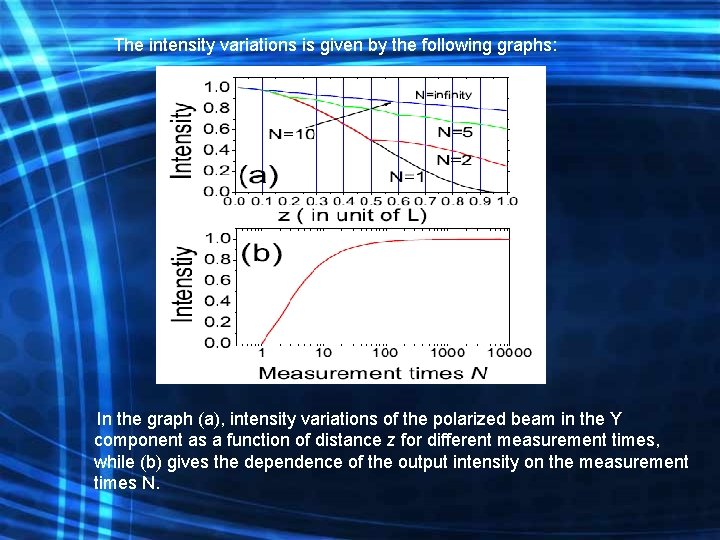
The intensity variations is given by the following graphs: In the graph (a), intensity variations of the polarized beam in the Y component as a function of distance z for different measurement times, while (b) gives the dependence of the output intensity on the measurement times N.

Zeno effect in Cancer Therapy § The application of the Zeno effect can be realized in many spheres of science, but one such crucial application being studied is in the field of ‘Cancer Therapy’. § The essential idea here is that the Zeno effect in practice, can allow for a pure-evolutionary self-destroying of the cancer without any active medical treatment. § Due to some quality work in this sphere by Serbian researchers namely Glavatović and Panković, we have got a very promising proposal of possibly treating cancer more effectively than the current medical methods.

§ The crux of the proposal lies in the concept of the inhibition of the regulator cells, which cause hyper-activity of the effector cells (also called as nature killer cells) that eliminate cancer cells (dirty inspector Harry effect). § It is an unambiguous fact that in the late stages of the disease, active medical treatment like chemo-therapy and chirurgic treatments can accelerate disease expansion rather than inhibition and hence it serves as a penalty function. The method using the Zeno effect does not have this disadvantage and hence is a promising option. § It has also been proven that the cancer cells affect the regular cells less and less effectively with the passage of time, so if the initial burst of the multiplication of the cells can be controlled, this can be an effective way to treat cancer. § Fundamentally, this stratagem is very similar to the Zeno effect in a non-stable system since in essence; it follows the notion that “Decay from an unstable state to the final decayed state can never take place if frequent perturbations are made my measurement (suitable medical treatment)”

§ Assume that tl corresponds to the time scale when population of the cancer cells is pl, where pl, represents the critical population of the cancer cells which almost certainly causes quick lethal effects. § The population of the cancer cells at a given time can be approximated as: p = p 0 (1 + at); where at << 1 and p <<pl, § Suppose that a suitable medical treatment exists which can be applied at the same moment (for a time interval significantly lower than t), then the equation reduces p to kp, so that k (1 + at) < 1 for at << 1. i. e. the population turns out to be pr = p 0 k(1 + at) <p 0 ; for at << 1

§ If the treatment is applied ‘n’ times, we can approximate the population as: prn = p 0 [(k (1 +at))n ] <p 0 for at << 1 Thus we see that formally as ‘n’ increases, the population tends to 0. i. e as N→ Infinity , prn → 0 It is not too hard to see that this describes the Zeno effect. § The main problem with this issue is the problem of finding the medical treatment, which would provide the necessary measurements. However, with the progress of nanofabrication technology and improvement in healthcare apparatus, such a process can be developed, and can radically impact the treatment of cancer.

Quantum Bomb Detection § One of the most widely touted applications of the QZE is the potential to solve the ‘Vaidaman’s Quantum Bomb’ problem. § The problem is posed as this: We have a package that may or may not contain a bomb. However the package is so sensitive that simply looking at it may cause that bomb to explode. § If this problem is posed classically, it turns out that this is unsolvable, however paradoxically quantum mechanics tells us that this is possible.

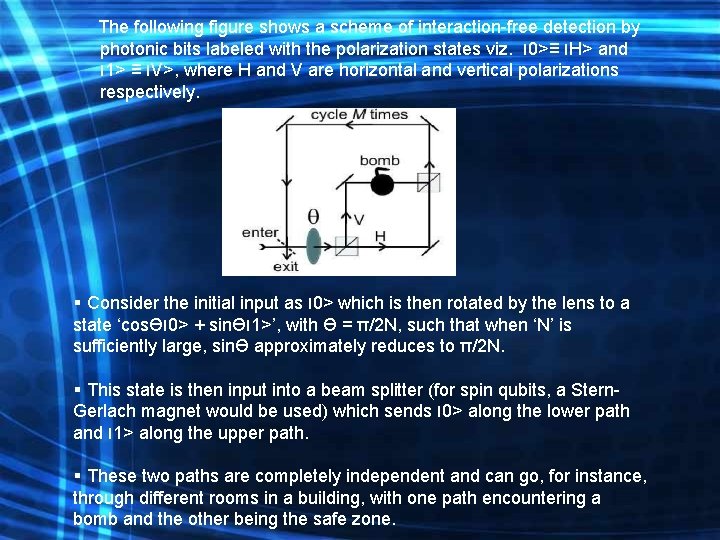
The following figure shows a scheme of interaction-free detection by photonic bits labeled with the polarization states viz. ׀ 0>≡ ׀ H> and ׀ 1> ≡ ׀ V>, where H and V are horizontal and vertical polarizations respectively. § Consider the initial input as ׀ 0> which is then rotated by the lens to a state ‘cosƟ ׀ 0> + sinƟ ׀ 1>’, with Ɵ = π/2 N, such that when ‘N’ is sufficiently large, sinƟ approximately reduces to π/2 N. § This state is then input into a beam splitter (for spin qubits, a Stern. Gerlach magnet would be used) which sends ׀ 0> along the lower path and ׀ 1> along the upper path. § These two paths are completely independent and can go, for instance, through different rooms in a building, with one path encountering a bomb and the other being the safe zone.

Consider two cases: Case 1 and Case 2 Case 1: No Bomb present Then the second beam splitter combines the amplitudes from the two paths coherently and the final state is ‘cosƟ ׀ 0> + sinƟ ׀ 1>’. If we send it for more iteration through the lens, we get ‘cos 2Ɵ ׀ 0> + sin 2Ɵ ׀ 1>’, so repeated iterations N times would give ‘cos. NƟ ׀ 0> + sin. NƟ ׀ 1>’ which would approximately equal ׀ 1>, since cos. NƟ becomes negligible. So if there is no bomb present and we follow the above scheme, and measure the state after N cycles, we get ׀ 1> with very high probability.

Case 2: Bomb Present in the room. Now suppose that there is a bomb in the room. Then there are two possible outcomes in the first cycle. With probability sin 2 Ɵ, the qubit passes the bomb and causes an explosion. With probability cos 2Ɵ, the qubit goes through the lower path, does not see the bomb, and emerges as ׀ 0>. Thus the presence of the bomb is like a quantum tortoise, which forces a quantum Zeno effect - but note that in this interferometric situation the bomb does not need to actually be measured and hence the name ‘interaction free measurement’. Now considering the second cycle, the probability that the bomb explodes is sin 2 Ɵ cos 2Ɵ whereas the probability of another avoidance is cos 2Ɵ. Therefore for N cycles, the probability for bomb avoidance is ‘cos 2 NƟ’ and the qubit emerges as ׀ 0>. And the probability that the bomb explodes in any one cycle between 1 to N is ‘ 1 - cos 2 NƟ’, but in the latter case there is no qubit. Thus we can solve the Vaidaman’s Bomb problem.

§ QZE has applications in a variety of fields like Neuroscience, Medicine, Philosophy etc. § It is thought to hold an enormous amount of potential in order to solve some of the problems that man has had to deal with. § With the advancement in technology, it is believed the mechanism of measurements would improve dramatically, and we would get very close to idealized measurements, which we have assumed in the various experimental proposals, thus solving the issue of continuous observation to a large extent. § Thus the sphere of QZE holds promising research potential.

Thank you for your patience….