Quantum Waves Applying Formulas from Waves Particles are

Quantum Waves Applying Formulas from Waves • Particles are actually waves – Two de Broglie relations • They have all the properties (and equations) that described waves before, together with some new ones • Rewrite the de Broglie relations in terms of k and : • We can also find a dispersion relation for these waves: • From this, we can find the group and phase velocity: “velocity” is group velocity, not phase velocity

Quantum Uncertainty Two uncertainty relations for any type of wave • Multiply by h-bar • Use quantum wave relations Uncertainty in Position/Momentum • Classical physics: – Particle is defined by position x and velocity v = (dx/dt) – Or, if you prefer, exact x and exact p • Quantum physics: – Particle is defined by wave function (x) – It cannot have a definite position and momentum – they tend to both be uncertain Uncertainty in Time/Energy • Things that last eternally can have definite energy • Things that last a brief time have uncertain energy – Measurements of energy will have a spread in value

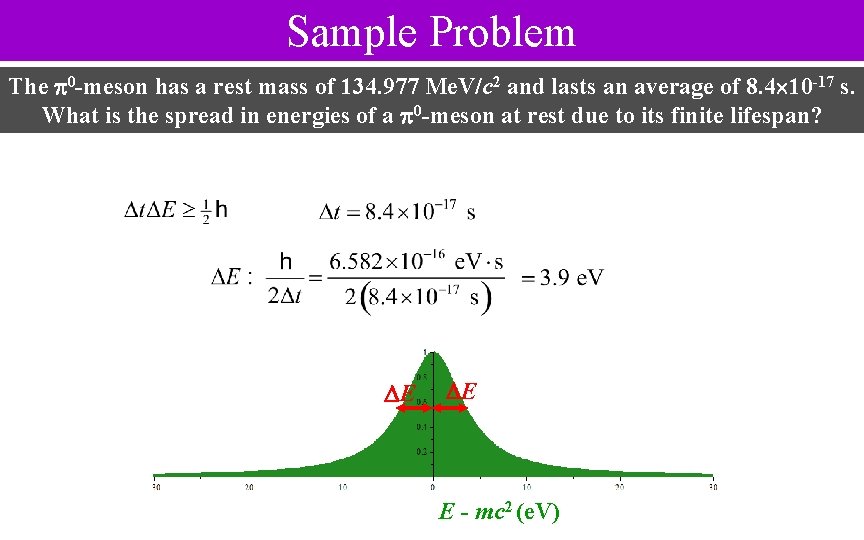
Sample Problem The 0 -meson has a rest mass of 134. 977 Me. V/c 2 and lasts an average of 8. 4 10 -17 s. What is the spread in energies of a 0 -meson at rest due to its finite lifespan? E E E - mc 2 (e. V)

Consequences of Position Uncertainty • Position and momentum of a particle cannot be simultaneously specified or determined • We can often estimate one quantity if we know the other by treating this inequality as if it were an equality – Especially when the energy is being minimized Energy of Particle in a Box ? • By Carlson’s rule, the position is uncertain by about x = ¼L. • By the uncertainty principle, momentum is uncertain by • We’d like the momentum to be zero, but we can’t • This causes the particle to have some energy, called Zero Point Energy These methods give only estimates of the answer L

Solving Uncertainty/Energy Problems A particle of mass m lies above an impenetrable barrier in a gravitational field with acceleration g. What is the minimum energy of the particle? 1. Write an expression for the energy: potential and kinetic 2. Figure out what momentum (normally 0) and what position would have the “ideal” lowest kinetic and potential energies 3. Let x = a and p = /2 a 4. Assume the momentum and position differ from ideal by about x = a and p = /2 a 5. Set derivative of energy function equal to zero, solve for a 6. Substitute a in to determine minimum energy m y

Uncertainty and the Hydrogen Atom (1) • There are two types of energy associated with the Hydrogen atom – Potential Energy – Kinetic Energy • Classically, these two energies are at a minimum when: – The electron is at rest, p = 0 – The electron is at the origin, r = 0 (x = 0) • In this case, the energy of the hydrogen atom E = – • Quantum mechanically, you can’t control both position and momentum – We will place the electron near the origin, r = 0, but there is an uncertainty x associated with it – We will place the electron nearly at rest, p = 0, but there is an uncertainty p associated with it – You have to compromise between these two choices to minimize E • Let x = a, and let p be as small as possible by the uncertainty principle • Substitute these into the formula for energy

Uncertainty and the Hydrogen Atom (2) We need to minimize the energy • Take derivative and set it to zero • Substitute result back in Correct answer is 4 times smaller than this. Why so far off? • It’s just an estimate • There is momentum in three dimensions – This makes answer 3 times smaller – Then answer we get is 4/3 of correct answer

The Wave Function • We’ve been talking about waves, which require wave functions – We’d better give it a name: – It would have more arguments in more dimensions • It is a complex function; it has both a real and imaginary parts – What does it mean? – This turns out to be very hard • Analogy: Electromagnetic Waves – Described by electric and magnetic fields • What is an electric field? • It is defined in terms of a potential for something American Heritage Science Dictionary “The distribution in space of the strength and direction of forces that would be exerted on an electric charge at any point in that space”. Dr. Carlson, PHY 114 “Electric Field is potential force at a distance on a charge”.

The Wave Function: What Does It Mean? • We are talking about one particle – but it is not at one location in space – If we measured its position, where would we be likely to find it? The Wave Function is also called the probability amplitude • Clearly, where the wave function is small (or zero), you wouldn’t expect to find the particle • Where it’s negative or imaginary, wouldn’t expect to have negative or imaginary probability – We’d better make sure that the probability is always positive • For electric fields, the energy density is proportional to the field squared – If working with complex waves, take amplitude first • How about we make probability density proportional to wave function magnitude squared:

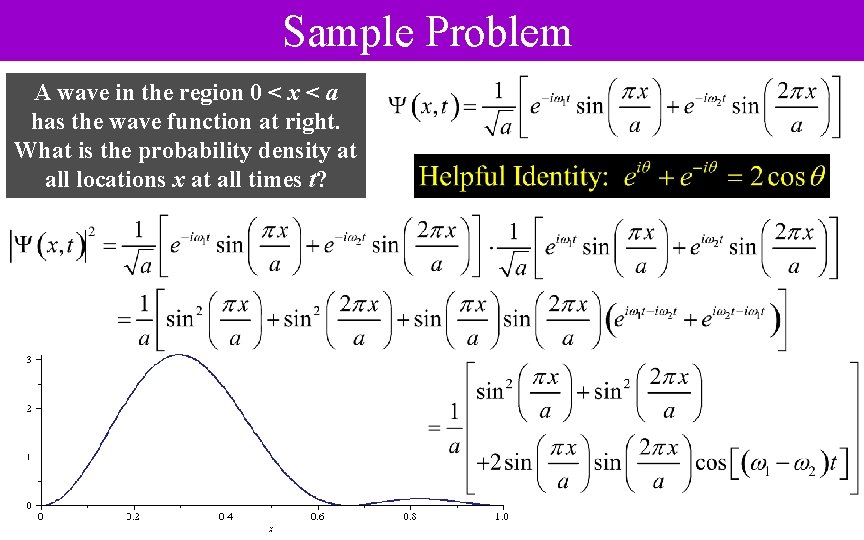
Sample Problem A wave in the region 0 < x < a has the wave function at right. What is the probability density at all locations x at all times t?

Announcements Day Today Wednesday Monday ASSIGNMENTS Read Quiz Secs. 5 -5 to 5 -7 Quiz O Section 6 -1 Quiz P Secs. 6 -2, 6 -5 Quiz Q A wave in the region 0 < x < a has the wave function at right. What is the probability density at all locations x at all times t? 10/7 Homework Hwk. O Hwk. P Hwk. Q

What Does Probability Density Mean? • The probability density (in 1 D) has units of m-1 – In a small region of size dx, the probability of finding the particle there is given by | |2 dx. • To find probability over a larger region, you have to integrate it Normalization: The probability that the particle is somewhere must be 1 • If we integrate over all x, we must get 1 … in the region • In some cases, the problem implies that we restrict to some 0<x<a … region

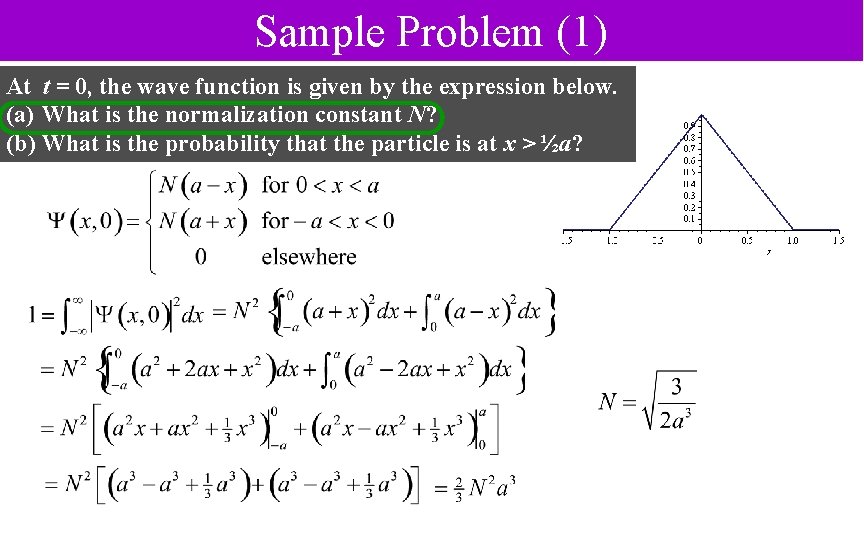
Sample Problem (1) At t = 0, the wave function is given by the expression below. (a) What is the normalization constant N? (b) What is the probability that the particle is at x > ½a?

Sample Problem (2) At t = 0, the wave function is given by the expression below. (a) What is the normalization constant N? (b) What is the probability that the particle is at x > ½a?

Sample Problem (1) At t = 0, the wave function is given by the expression at right. (a) What is the most likely / least likely places to find the particle? (b) What is the normalization constant N? (c) What is the probability that the particle is at 0 < x < a? • Least likely when function vanishes, at x = 0 • Most likely when function is largest positive or negative Normalization: • Let x = atan

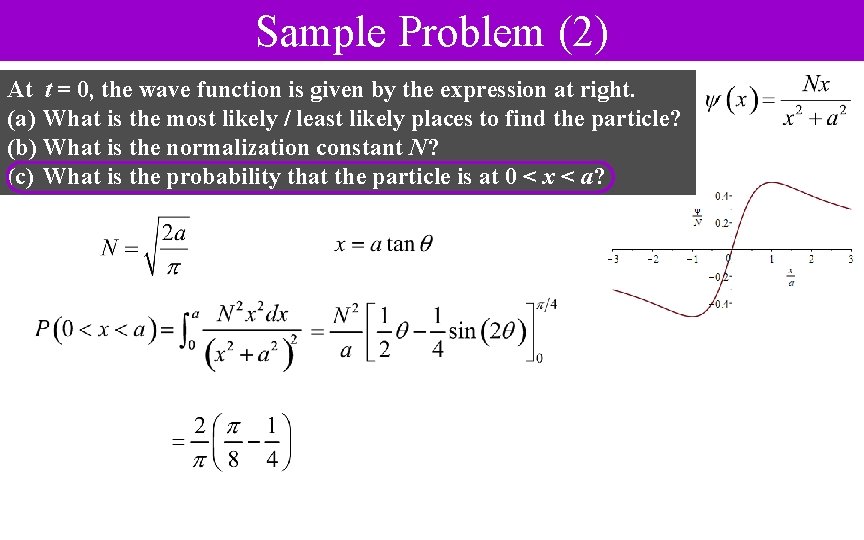
Sample Problem (2) At t = 0, the wave function is given by the expression at right. (a) What is the most likely / least likely places to find the particle? (b) What is the normalization constant N? (c) What is the probability that the particle is at 0 < x < a?

Quantum Wave Equations You Need: End of material for Test 2