Quantum Theory and the Electronic Structure of Atoms

Quantum Theory and the Electronic Structure of Atoms Chapter 7 1 Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

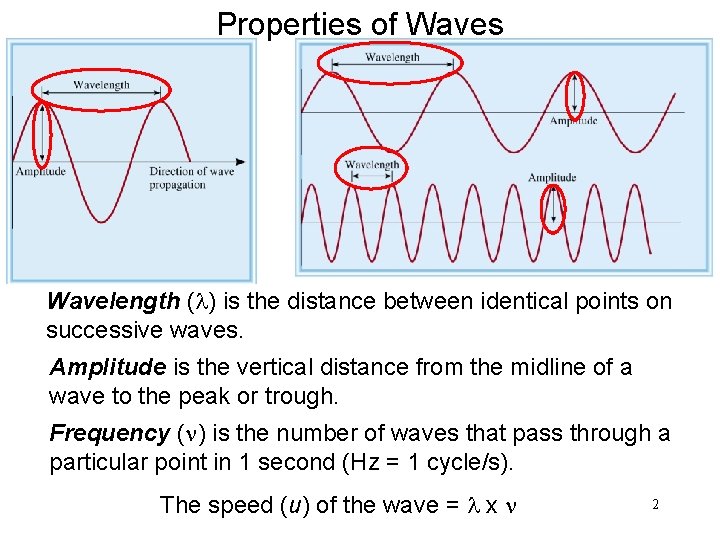
Properties of Waves Wavelength (l) is the distance between identical points on successive waves. Amplitude is the vertical distance from the midline of a wave to the peak or trough. Frequency (n) is the number of waves that pass through a particular point in 1 second (Hz = 1 cycle/s). The speed (u) of the wave = l x n 2

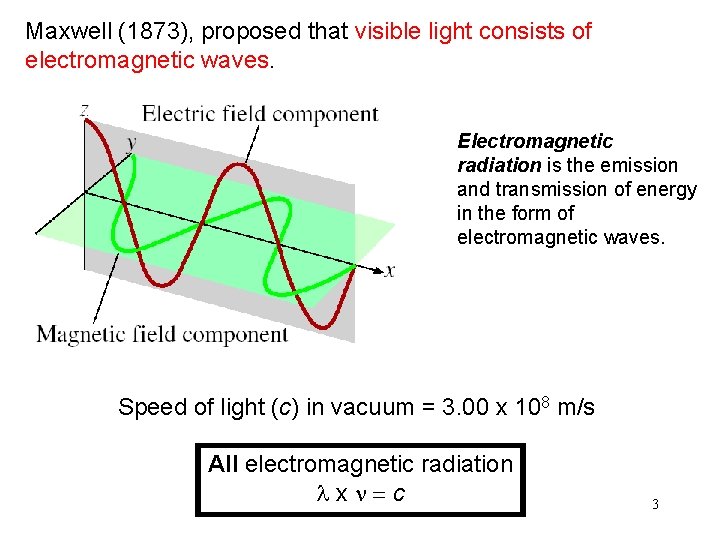
Maxwell (1873), proposed that visible light consists of electromagnetic waves. Electromagnetic radiation is the emission and transmission of energy in the form of electromagnetic waves. Speed of light (c) in vacuum = 3. 00 x 108 m/s All electromagnetic radiation l x n = c 3

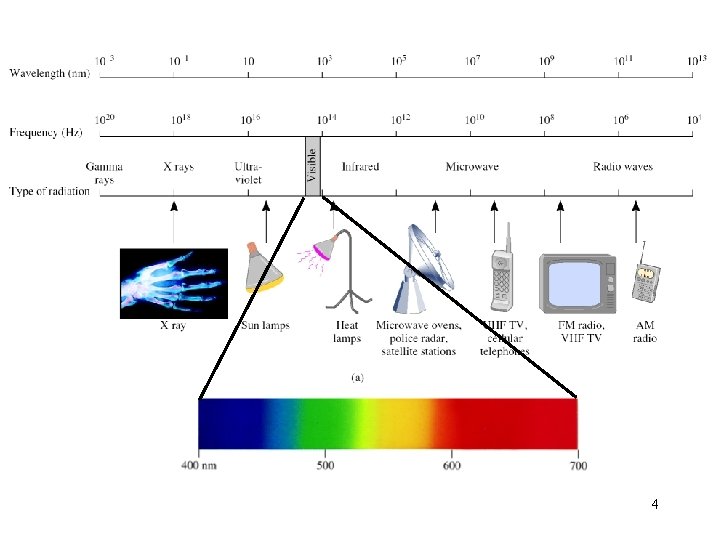
4

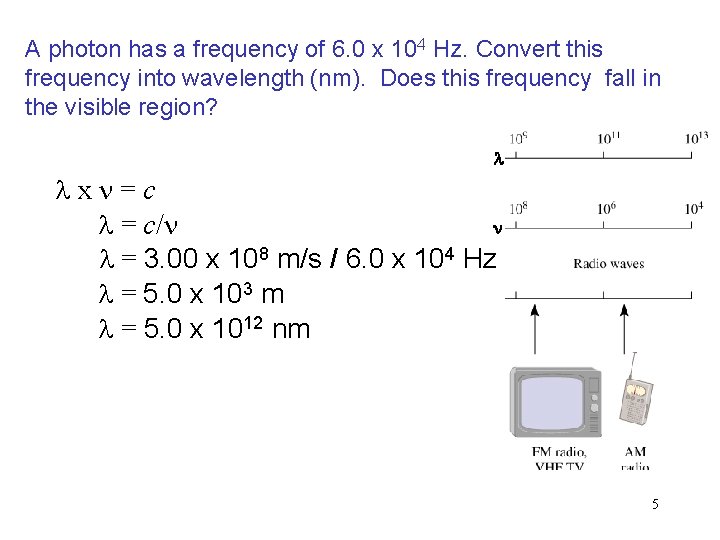
A photon has a frequency of 6. 0 x 104 Hz. Convert this frequency into wavelength (nm). Does this frequency fall in the visible region? l lxn=c n l = c/n l = 3. 00 x 108 m/s / 6. 0 x 104 Hz l = 5. 0 x 103 m l = 5. 0 x 1012 nm 5

Mystery #1, “Heated Solids Problem” Solved by Planck in 1900 When solids are heated, they emit electromagnetic radiation over a wide range of wavelengths. Radiant energy emitted by an object at a certain temperature depends on its wavelength. Energy (light) is emitted or absorbed in discrete units (quantum). E = h x n Planck’s constant (h) h = 6. 63 x 10 -34 J • s 6

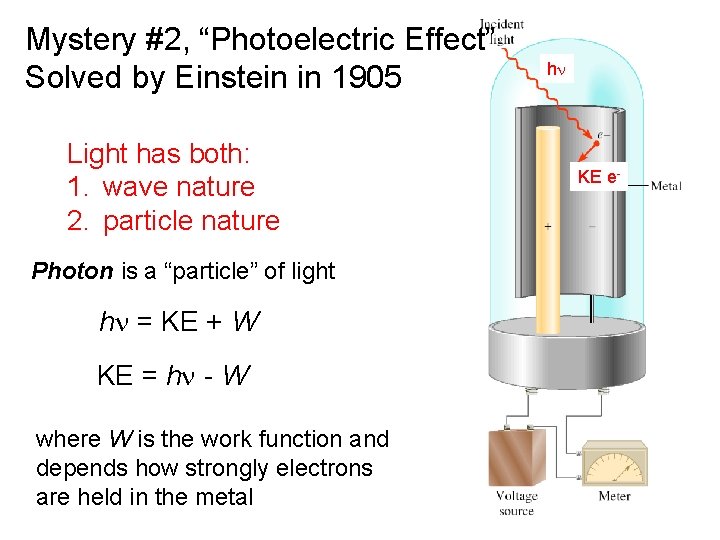
Mystery #2, “Photoelectric Effect” Solved by Einstein in 1905 Light has both: 1. wave nature 2. particle nature hn KE e- Photon is a “particle” of light hn = KE + W KE = hn - W where W is the work function and depends how strongly electrons are held in the metal 7

When copper is bombarded with high-energy electrons, X rays are emitted. Calculate the energy (in joules) associated with the photons if the wavelength of the X rays is 0. 154 nm. E = h x n E = h x c / l E = 6. 63 x 10 -34 (J • s) x 3. 00 x 10 8 (m/s) / 0. 154 x 10 -9 (m) E = 1. 29 x 10 -15 J 8

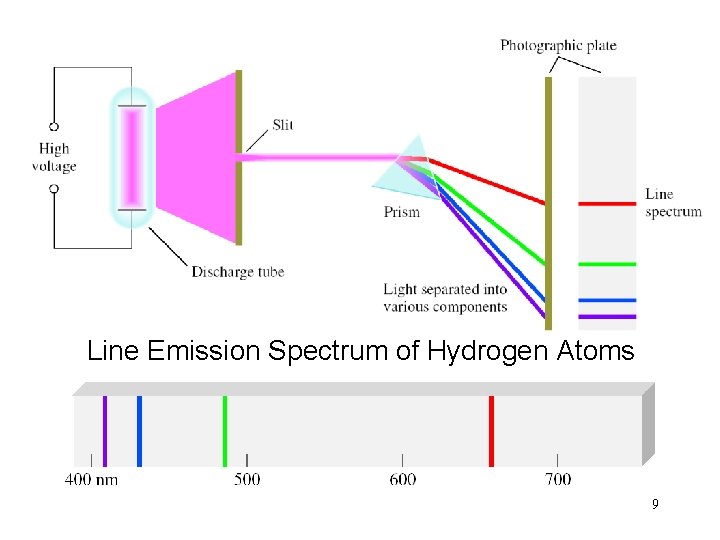
Line Emission Spectrum of Hydrogen Atoms 9

10

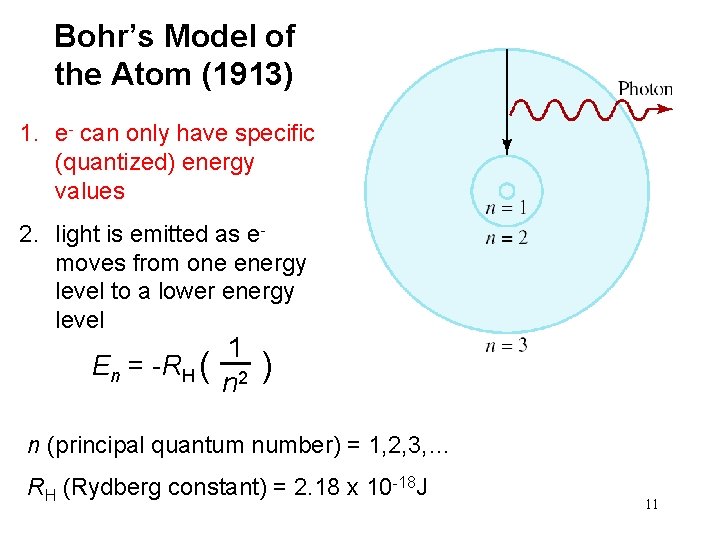
Bohr’s Model of the Atom (1913) 1. e- can only have specific (quantized) energy values 2. light is emitted as e- moves from one energy level to a lower energy level 1 En = -RH ( ) n 2 n (principal quantum number) = 1, 2, 3, … RH (Rydberg constant) = 2. 18 x 10 -18 J 11

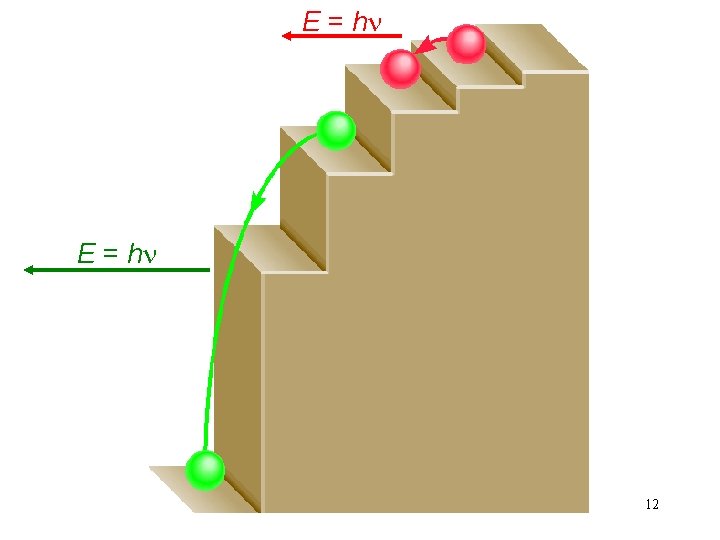
E = hn 12

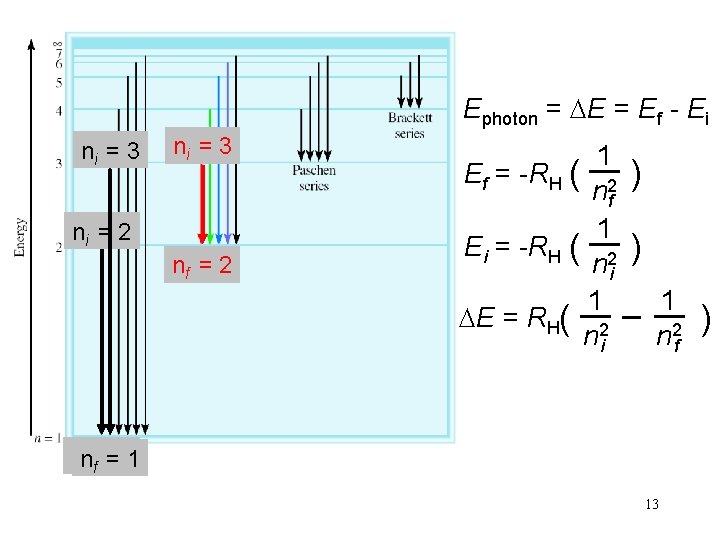
Ephoton = Ef - Ei ni = 3 ni = 2 nf = 2 1 Ef = -RH ( ) n 2 f 1 Ei = -RH ( ) n 2 i 1 1 E = RH( ) n 2 i n 2 f nnf f= 1 13

14

Calculate the wavelength (in nm) of a photon emitted by a hydrogen atom when its electron drops from the n = 5 state to the n = 3 state. 1 1 Ephoton = E = RH( ) n 2 i n 2 f Ephoton = 2. 18 x 10 -18 J x (1/25 - 1/9) Ephoton = E = -1. 55 x 10 -19 J Ephoton = h x c / l l = h x c / Ephoton l = 6. 63 x 10 -34 (J • s) x 3. 00 x 108 (m/s)/1. 55 x 10 -19 J l = 1280 nm 15

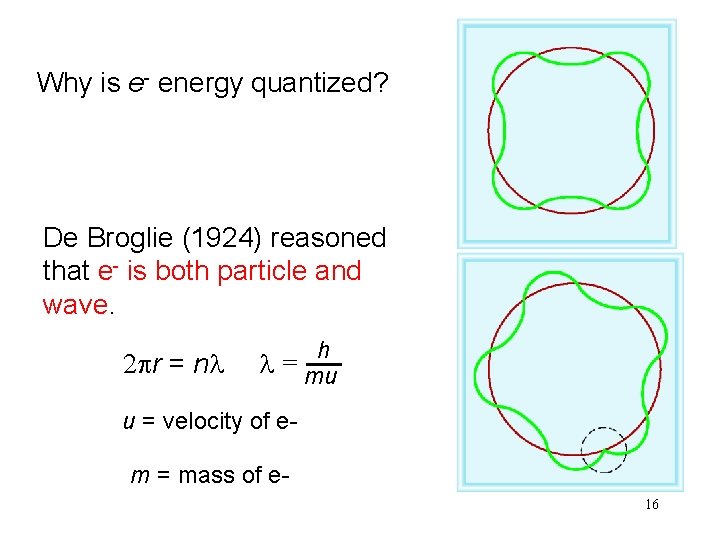
Why is e- energy quantized? De Broglie (1924) reasoned that e- is both particle and wave. 2 pr = nl h l = mu u = velocity of e- m = mass of e 16

The Wave Nature of Matter • Louis de Broglie posited ﺃﺜﺒﺖ that if light can have material properties, matter should exhibit wave properties. • He demonstrated that the relationship between mass and wavelength was h = mv Electronic Structure of Atoms

What is the de Broglie wavelength (in nm) associated with a 2. 5 g Ping-Pong ball traveling at 15. 6 m/s? l = h/mu h in J • s m in kg u in (m/s) l = 6. 63 x 10 -34 / (2. 5 x 10 -3 x 15. 6) l = 1. 7 x 10 -32 m = 1. 7 x 10 -23 nm J = m 2 kgs-2 18

The Uncertainty Principle ﻟﻬﺎﻳﺰﻧﺒﻴﺮﺝ ﺍﻟﺘﺄﻜﺪ ﻋﺪﻡ ﻣﺒﺪﺃ • Heisenberg showed that the more precisely the momentum of a particle is known, the less precisely is its position known: ( x) ( mv) h 2 • In many cases, our uncertainty of the whereabouts of an electron is greater than the size of the atom itself! Electronic Structure of Atoms

• What does the uncertainty principle mean? • The uncertainty principle also called the Heisenberg Uncertainty Principle, articulated (1927) by the German physicist Werner Heisenberg, that the position and the velocity of an object cannot both be measured exactly, at the same time, even in theory. • What did the uncertainty principle state? • The Heisenberg uncertainty principle states that it is impossible to know simultaneously the exact position and momentum of a particle. That is, the more exactly the position is determined, the less known the momentum, and vice versa. Electronic Structure of Atoms

Schrodinger’s Wave Equation Erwin Schrodinger Equation for the probability of a single electron being found along a single axis (x-axis) (this slide from: J. Hushen’s presentation on Atomic Structure at http: //teachers. greenville. k 12. sc. us/sites/jhushen/Pages/AP%20 Chemistry. aspx) Electronic Structure of Atoms

Schrodinger Wave Equation In 1926 Schrodinger wrote an equation that described both the particle and wave nature of the e. Wave function (y) describes: 1. energy of e- with a given y 2. probability of finding e- in a volume of space Schrodinger’s equation can only be solved exactly for the hydrogen atom. Must approximate its solution for multi-electron systems. 23

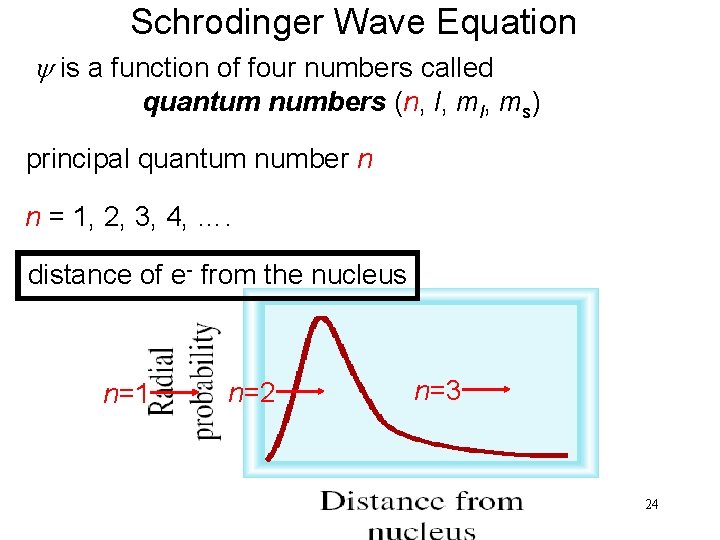
Schrodinger Wave Equation y is a function of four numbers called quantum numbers (n, l, ms) principal quantum number n n = 1, 2, 3, 4, …. distance of e- from the nucleus n=1 n=2 n=3 24

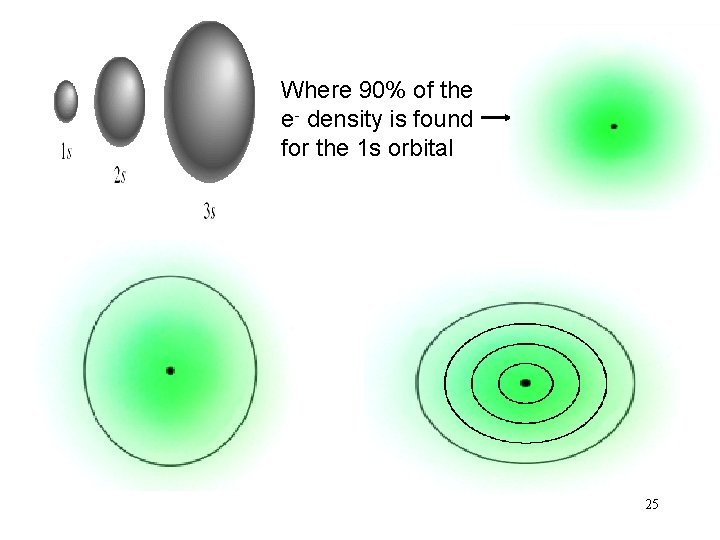
Where 90% of the e- density is found for the 1 s orbital 25

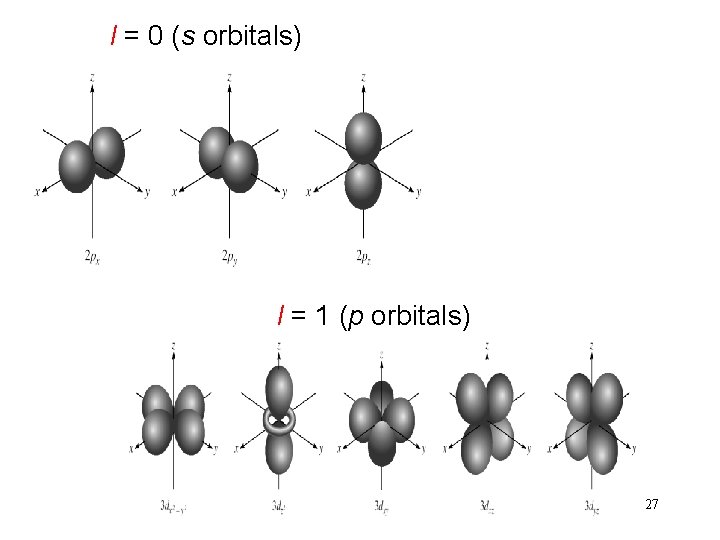
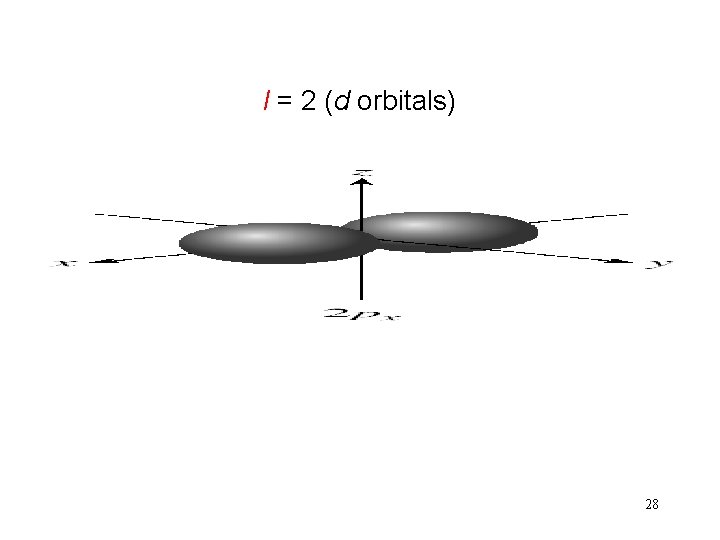
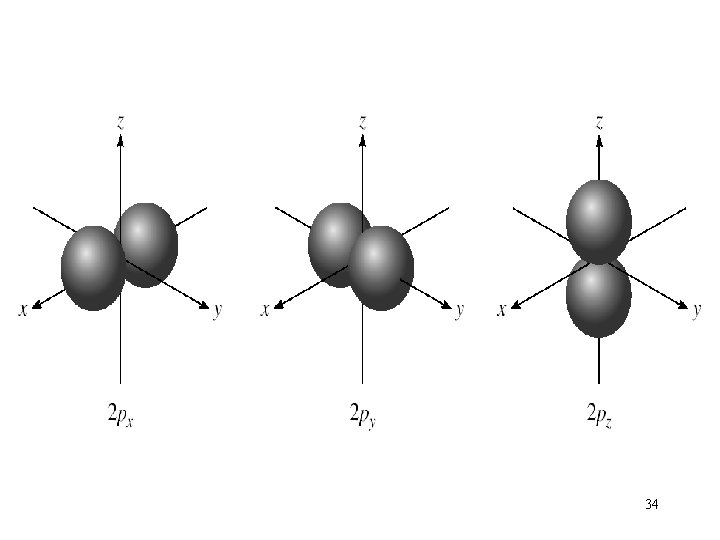
Schrodinger Wave Equation quantum numbers: (n, l, ms) angular momentum quantum number l for a given value of n, l = 0, 1, 2, 3, … n-1 n = 1, l = 0 n = 2, l = 0 or 1 n = 3, l = 0, 1, or 2 l = 0 s orbital l = 1 p orbital l = 2 d orbital l = 3 f orbital Shape of the “volume” of space that the e- occupies 26

l = 0 (s orbitals) l = 1 (p orbitals) 27

l = 2 (d orbitals) 28

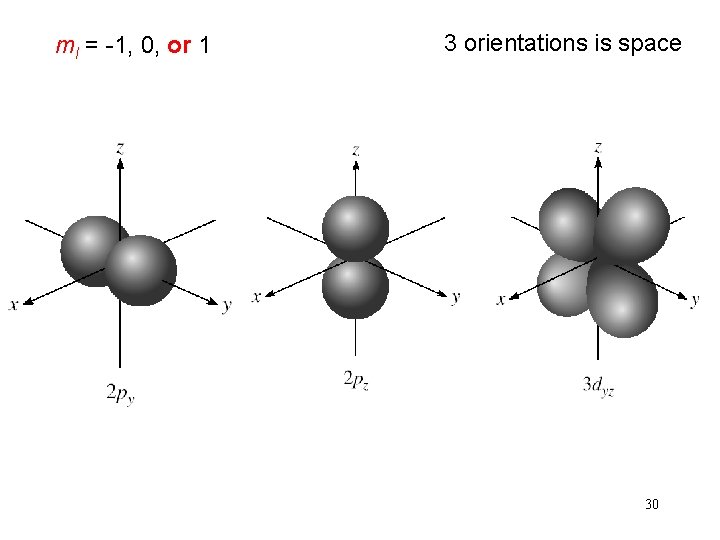
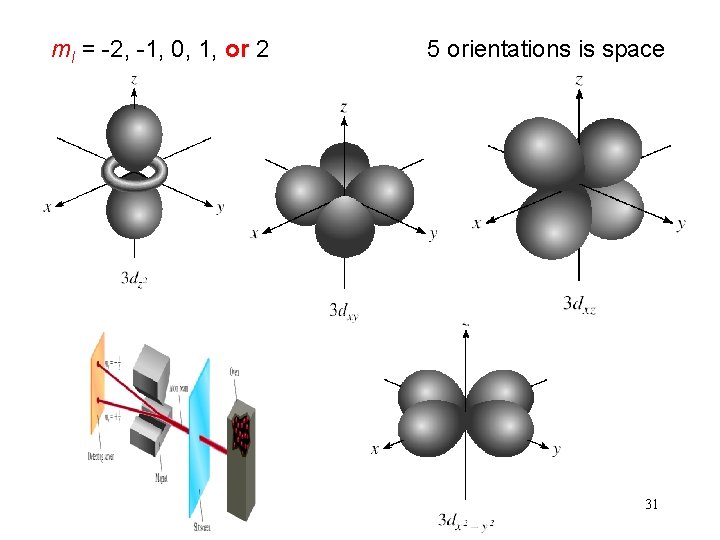
Schrodinger Wave Equation quantum numbers: (n, l, ms) magnetic quantum number ml for a given value of l ml = -l, …. , 0, …. +l if l = 1 (p orbital), ml = -1, 0, or 1 if l = 2 (d orbital), ml = -2, -1, 0, 1, or 2 orientation of the orbital in space 29

ml = -1, 0, or 1 3 orientations is space 30

ml = -2, -1, 0, 1, or 2 5 orientations is space 31

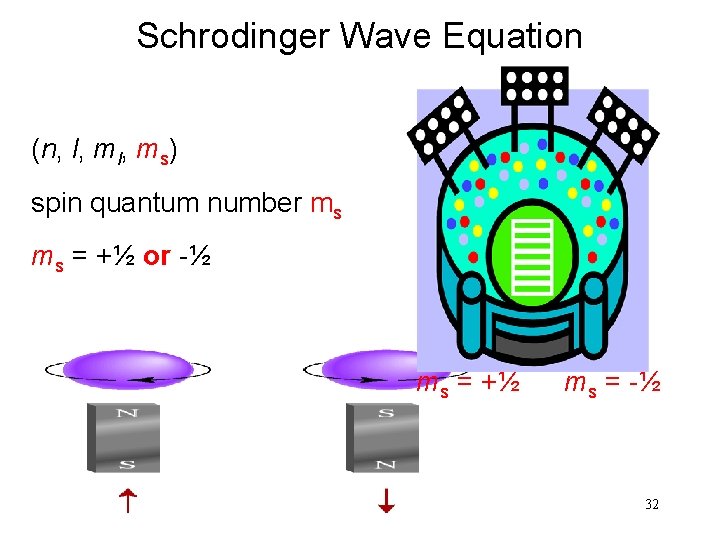
Schrodinger Wave Equation (n, l, ms) spin quantum number ms ms = +½ or -½ ms = +½ ms = -½ 32

Schrodinger Wave Equation quantum numbers: (n, l, ms) Existence (and energy) of electron in atom is described by its unique wave function y. Pauli exclusion principle - no two electrons in an atom can have the same four quantum numbers. Each seat is uniquely identified (E, R 12, S 8) Each seat can hold only one individual at a time 33

34

Schrodinger Wave Equation quantum numbers: (n, l, ms) Shell – electrons with the same value of n Subshell – electrons with the same values of n and l Orbital – electrons with the same values of n, l, and ml How many electrons can an orbital hold? If n, l, and ml are fixed, then ms = ½ or - ½ y = (n, l, ml, ½) or y = (n, l, ml, -½) An orbital can hold 2 electrons 35

How many 2 p orbitals are there in an atom? n=2 2 p If l = 1, then ml = -1, 0, or +1 3 orbitals l = 1 How many electrons can be placed in the 3 d subshell? n=3 3 d l = 2 If l = 2, then ml = -2, -1, 0, +1, or +2 5 orbitals which can hold a total of 10 e 36

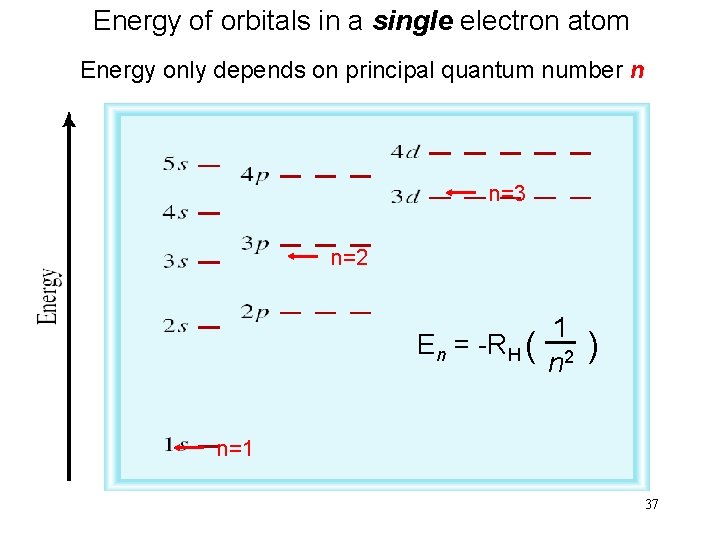
Energy of orbitals in a single electron atom Energy only depends on principal quantum number n n=3 n=2 1 En = -RH ( ) n 2 n=1 37

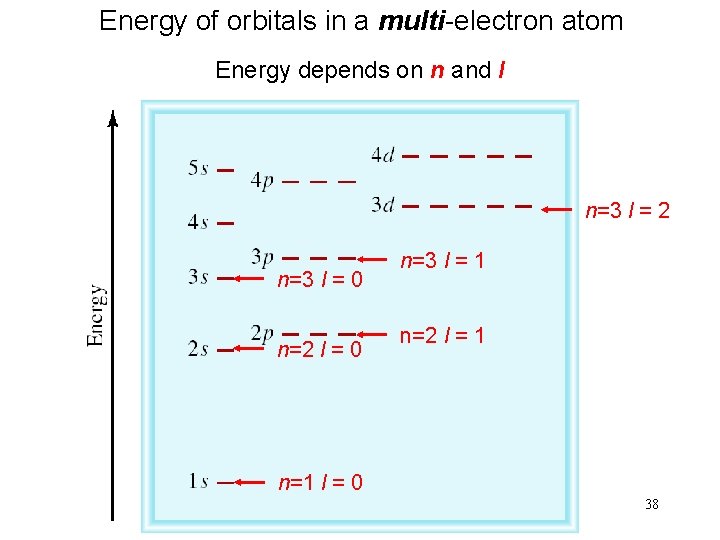
Energy of orbitals in a multi-electron atom Energy depends on n and l n=3 l = 2 n=3 l = 0 n=2 l = 0 n=3 l = 1 n=2 l = 1 n=1 l = 0 38

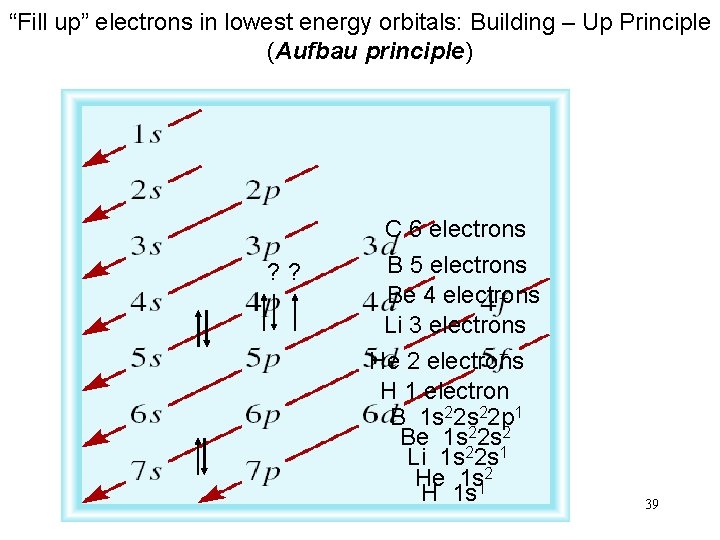
“Fill up” electrons in lowest energy orbitals: Building – Up Principle (Aufbau principle) ? ? C 6 electrons B 5 electrons Be 4 electrons Li 3 electrons He 2 electrons H 1 electron B 1 s 22 p 1 Be 1 s 22 s 2 Li 1 s 22 s 1 He 1 s 12 H 1 s 39

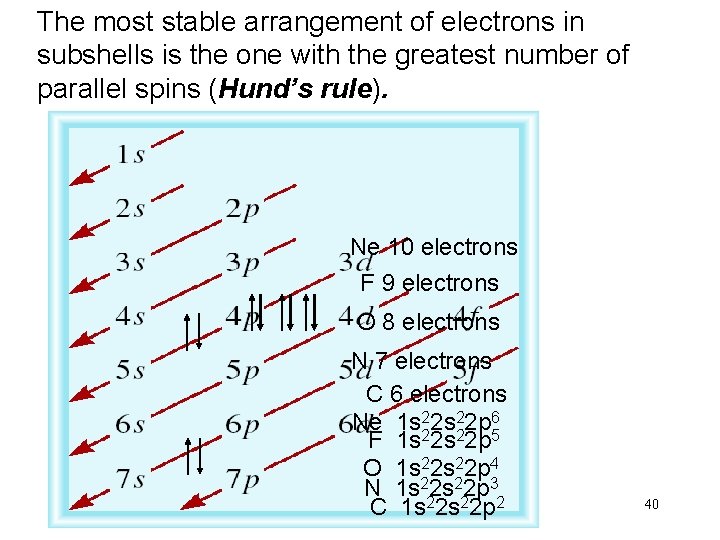
The most stable arrangement of electrons in subshells is the one with the greatest number of parallel spins (Hund’s rule). Ne 10 electrons F 9 electrons O 8 electrons N 7 electrons C 6 electrons Ne 1 s 222 p 65 F 1 s 2 s 2 p O 1 s 22 p 4 N 1 s 222 p 32 C 1 s 2 s 2 p 40

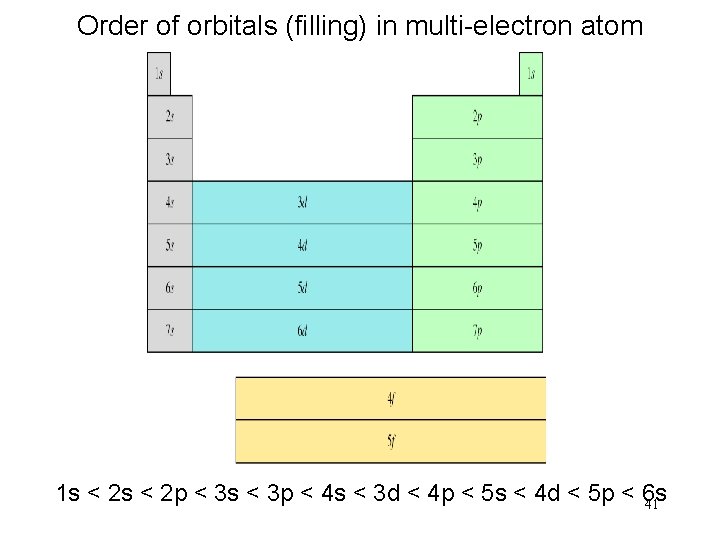
Order of orbitals (filling) in multi-electron atom 1 s < 2 p < 3 s < 3 p < 4 s < 3 d < 4 p < 5 s < 4 d < 5 p < 6 s 41

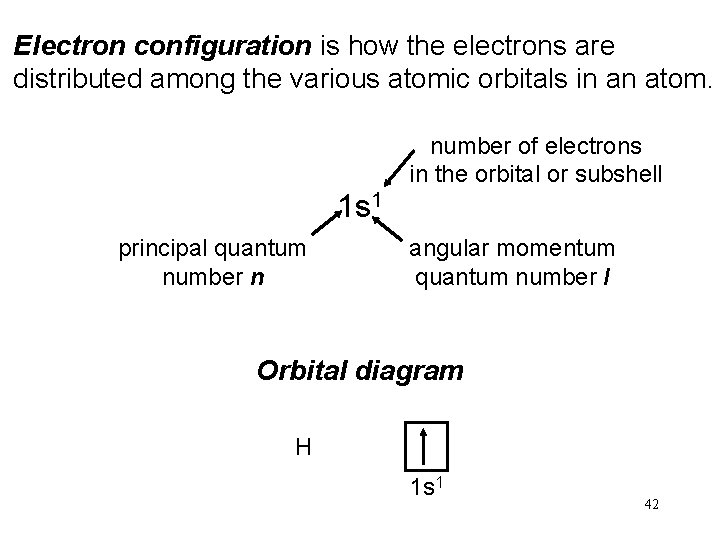
Electron configuration is how the electrons are distributed among the various atomic orbitals in an atom. number of electrons in the orbital or subshell 1 s 1 principal quantum number n angular momentum quantum number l Orbital diagram H 1 s 1 42

What is the electron configuration of Mg? Mg 12 electrons 1 s < 2 p < 3 s < 3 p < 4 s 1 s 22 p 63 s 2 2 + 6 + 2 = 12 electrons Abbreviated as [Ne]3 s 2 [Ne] 1 s 22 p 6 What are the possible quantum numbers for the last (outermost) electron in Cl? Cl 17 electrons 1 s 22 p 63 s 23 p 5 1 s < 2 p < 3 s < 3 p < 4 s 2 + 6 + 2 + 5 = 17 electrons Last electron added to 3 p orbital n = 3 l = 1 ml = -1, 0, or +1 ms = ½ or -½ 43

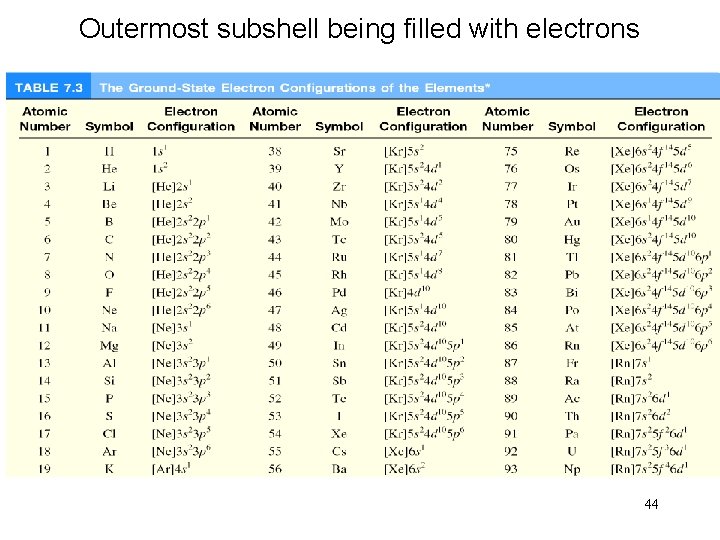
Outermost subshell being filled with electrons 44

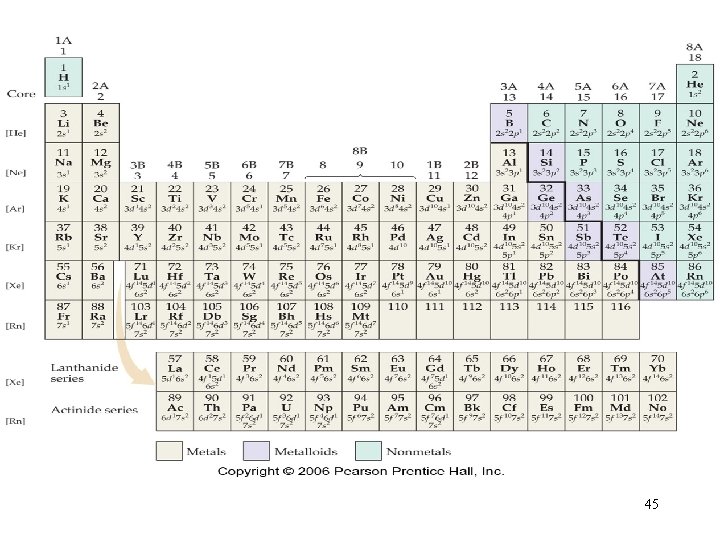
45

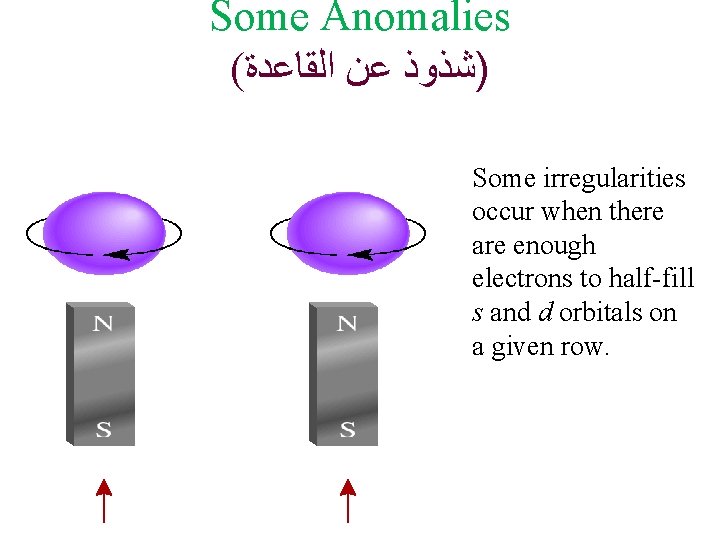
Some Anomalies ( )ﺷﺬﻭﺫ ﻋﻦ ﺍﻟﻘﺎﻋﺪﺓ Some irregularities occur when there are enough electrons to half-fill s and d orbitals on a given row.

Some Anomalies For instance, the electron configuration for chromium is [Ar] 4 s 1 3 d 5 rather than the expected [Ar] 4 s 2 3 d 4 Copper is [Ar] 4 s 1 3 d 10 rather than the expected [Ar] 4 s 23 d 9

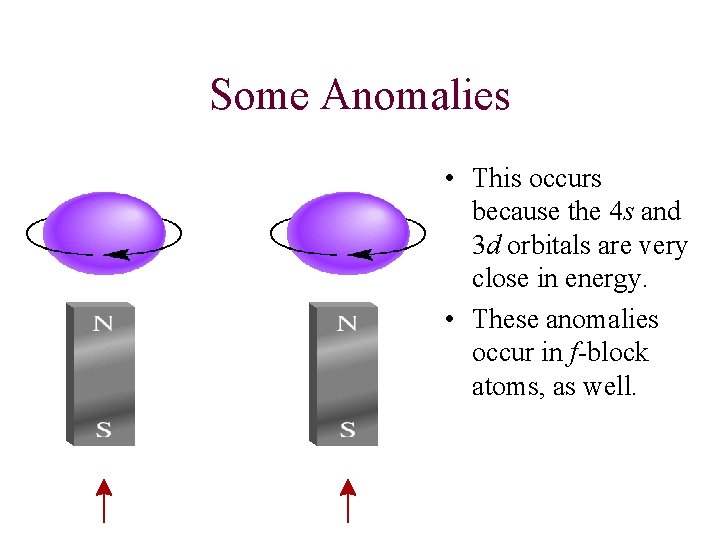
Some Anomalies • This occurs because the 4 s and 3 d orbitals are very close in energy. • These anomalies occur in f-block atoms, as well.

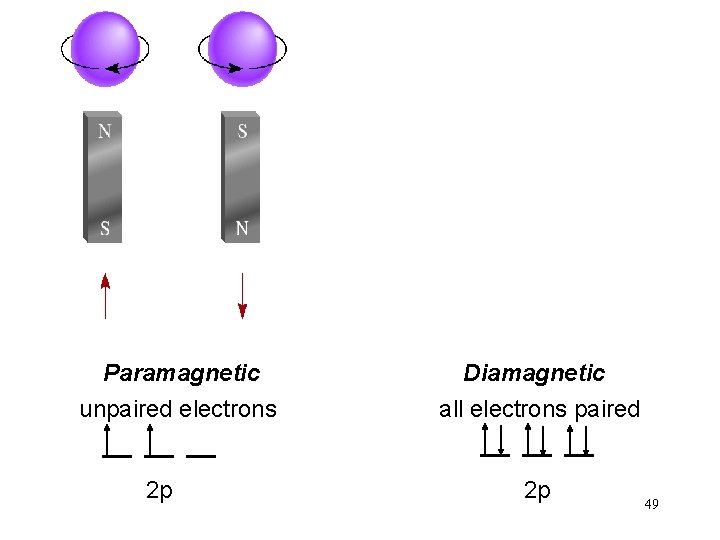
Paramagnetic unpaired electrons 2 p Diamagnetic all electrons paired 2 p 49

The shielding Effect ﺗﺄﺜﻴﺮ ﺍﻟﺤﺠﺐ ﻓﻲ ﺍﻟﺬﺭﺍﺕ ﻣﺘﻌﺪﺩﺓ ﺍﻹﻟﻜﺘﺮﻭﻧﺎﺕ • The shielding effect describes the attraction between an electron and the nucleus in any atom with more than one electron shell. Shielding effect can be defined as a reduction in the Effective Nuclear Charge on the electron cloud, due to a difference in the attraction forces of the electrons on the nucleus. • In hydrogen, or any other atom in group 1 A of the periodic table (those with only one valence electron), the force on the electron is just as large as the electromagnetic attraction from the nucleus. However, when more electrons are involved, each electron (in the nth-shell) experiences not only the electromagnetic attraction from the positive nucleus, but also repulsion forces from other electrons in shells from 1 to n. This causes the net force on electrons in outer shells to be significantly smaller in magnitude; therefore, these electrons are not as strongly bonded to the nucleus as electrons closer to the nucleus. This phenomenon is often referred to as the orbital penetration effect. The shielding theory also contributes to the explanation of why © 2009, Prentice-Hall, Inc. valence -shell electrons are more easily removed from the atom