Quantum Statistics Chapter 9 in Reifs Book many

Quantum Statistics Chapter 9 in Reif’s Book + many other sources Overview! Applications will be discussed as we proceed

Some History! “The [Fermi-Dirac] function is probably the correct one for gas molecules, since it is known to be the correct one for electrons in an atom, & one would expect molecules to resemble electrons more closely than light quanta”. P. A. M. Dirac (1926)

Some History! Apparently, Pauli felt emotionally about which type of statistics to use! “With a heavy heart, I have become converted to the idea that Fermi-Dirac and not Bose Einstein, is the correct statistics [for electrons]”. W. Pauli to E. Schrödinger (1926)

Quantuml Statistics Maxwell-Boltzmann (Classical) Statistics Everything in Classical Thermo & Stat Mech!

Quantum Statistics 1. Fermi-Dirac Statistics • Fermions: Particles with odd half-integer spin. • Detailed treatment of The Free Electron Gas 1 a. Applications to Conduction Electrons in Metals

Quantum Statistics 1. Fermi-Dirac Statistics • Fermions: Particles with odd half-integer spin. • Brief overview of treatment of The Neutron Gas 1 b. Applications to Neutron Star Matter

Quantum Statistics 2. Bose-Einstein Statistics • Bosons: Particles with integer spin. Planck or • Detailed treatment of Photon Statistics The Photon Gas 2 a. Applications to Black Body Radiation.

Quantum Statistics 2. Bose-Einstein Statistics • Bosons: Particles with integer spin. • Overview of treatment of The Boson Gas 2 b. Applications to: c. Superfluid liquid He d. Superconductivity in some solids. e. Bose-Einstein Condensation

Review of Classical (Maxwell. Boltzmann) Statistics Maxwell-Boltzmann (MB) Distribution: • Comes from the Canonical Ensemble. • For a system in thermodynamic equilibrium, the probability of finding it with energy Es at temperature T is β [1/(k. BT)]

• The Canonical Ensemble result for the probability of finding the system in equilibrium with energy E at temperature T is written in what follows as: β [1/(k. BT)] A = Normalization Constant -1 (Partition Function)

MB Distribution • The probability of finding a system with energy E at temperature T is • Define: n(E)d. E number of particles with energies between E & E + d. E. • Define: g(E) Density of States number of states available per unit energy range. • The functional form of g(E) depends on the microscopic details of each system. We then have For free electrons, g(E) (E)½

Quantum Distributions The characteristic of Indistinguishablity makes quantum statistics VERY different from classical statistics!!!!! • For example, consider the possible configurations for 2 DISTINGUISHABLE particles A & B which can be in either of 2 energy states: State 1 State 2 AB A B B A AB Probability of each configuration (¼)

• But, if the particles are Indistinguishable A= B = X, the possible configurations are: State 1 State 2 XX X X L XX Probability of each configuration (⅓) • A proper quantum mechanical treatment of particle statistics MUST account for the Indistinguishablity of identical particles.

Example from earlier in the course: • Consider a System of N = 3 Particles, fixed in position, each with spin = ½ Each spin is either “up” (↑, m = ½) or “down” (↓, m = -½). • Each particle has a vector magnetic moment μ. • The projection of μ along a “z-axis” is either: μz = μ, for spin “up” or μz = -μ, for spin “down”

• Put this system in an External Magnetic Field H. • Classical E&M tells us that a magnetic moment μ in an external field H has energy: ε = - μ H • Combine this with the Quantum result: Each particle has 2 possible energies: ε+ ≡ - μH for spin “up” ε- ≡ μH for spin “down” For 3 particles, the State of the system is specified by specifying each m = There are (2)3 = 8 Possible States!

Possible States of a 3 Spin System (Distinguishable Spins) • Counting states as if the 3 spins were distinguishable, clearly gives 8 possible microstates for this 3 spin system!

Possible States of a 3 Spin System (Indistinguishable Spins) 1 2 Equivalent states! 3 Equivalent states! 4 • Counting instead as if the 3 spins were indistinguishable, clearly gives only 4 possible microstates for this 3 spin system!

Pauli Exclusion Principle “No 2 Fermions can occupy the same single particle quantum state” • This principle is obeyed by some quantum mechanical particles (Fermions) & is not obeyed by others (Bosons). So, when doing Statistics, it is necessary to distinguish between 2 Categories of Quantum Particles. 2 Kinds of Quantum Statistics are also needed.

2 Categories of Quantum Particles & 2 Kinds of Quantum Statistics are needed: Fermions Particles with odd half integer spin. Obey the Pauli Exclusion Principle.

2 Categories of Quantum Particles & 2 Kinds of Quantum Statistics are needed: Bosons Particles with integer spin. Don’t Obey the Pauli Exclusion Principle (Integer spin includes spin = 0).

Quantum Distribution Functions For Fermions, The Fermi-Dirac Distribution is needed: FFD “Fermi Function” where • B 1 is a normalization constant related to the Chemical Potential (Fermi Energy). • This will be discussed shortly.

More standard notation for The Fermi-Dirac Distribution is: The Chemical Potential ( Fermi Energy EF or F). • More details of this will be discussed soon.

For Bosons, The Bose-Einstein Distribution is needed: FBE “Bose Function” where • B 2 is a normalization constant related to the Chemical Potential • This will be discussed shortly.

More standard notation for The Bose-Einstein Distribution is: The Chemical Potential • More details of this will be discussed soon.

Summary: Quantum Distribution Functions Fermi-Dirac Distribution Bose-Einstein Distribution

Classical Limit of the Quantum Distributions • The Fermi-Dirac Distribution & the Bose Einstein Distribution both reduce to the Classical Maxwell. Boltzmann (MB) Distribution in The Classical Limit High Temperature Limit

Classical Limit of the Quantum Distributions • In the Classical (High Temperature) Limit, both the Fermi-Dirac Distribution & the Bose Einstein Distribution reduce to the Classical Maxwell-Boltzmann (MB) Distribution. This happens when Biexp(βE) << 1. • Equivalently, they reduce to the MB distribution when Aexp(−βE) << 1.

Classical Limit of the Quantum Distributions • That is, in the Classical (High Temperature) Limit, and l

Classical & Quantum Distributions B 2 exp(-βμ) μ “Chemical Potential” B 1 exp(-βμ) exp(-βEF) EF “Fermi Energy”

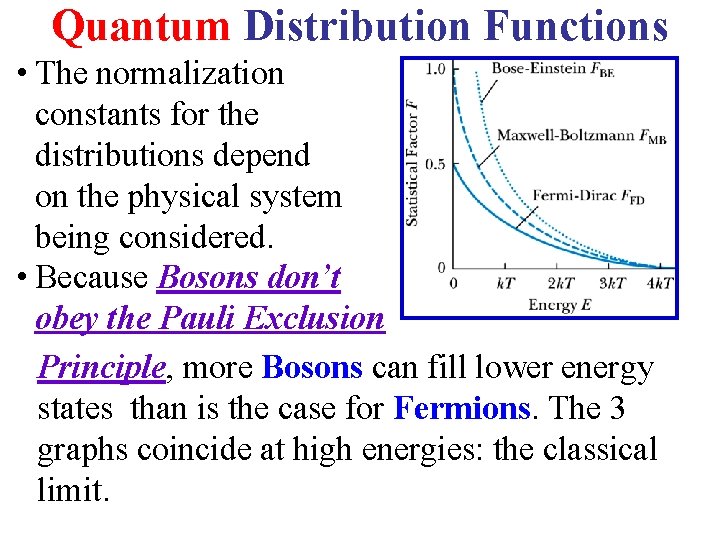
Quantum Distribution Functions • The normalization constants for the distributions depend on the physical system being considered. • Because Bosons don’t obey the Pauli Exclusion Principle, more Bosons can fill lower energy states than is the case for Fermions. The 3 graphs coincide at high energies: the classical limit.

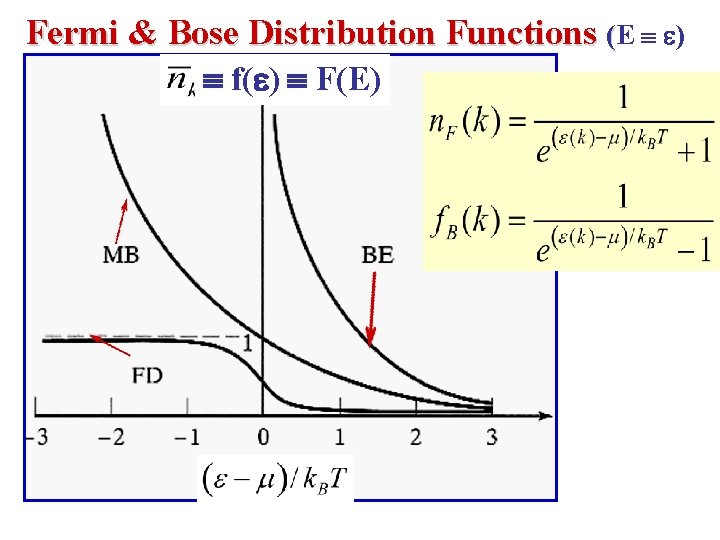
Fermi & Bose Distribution Functions (E ) f( )o F(E) or

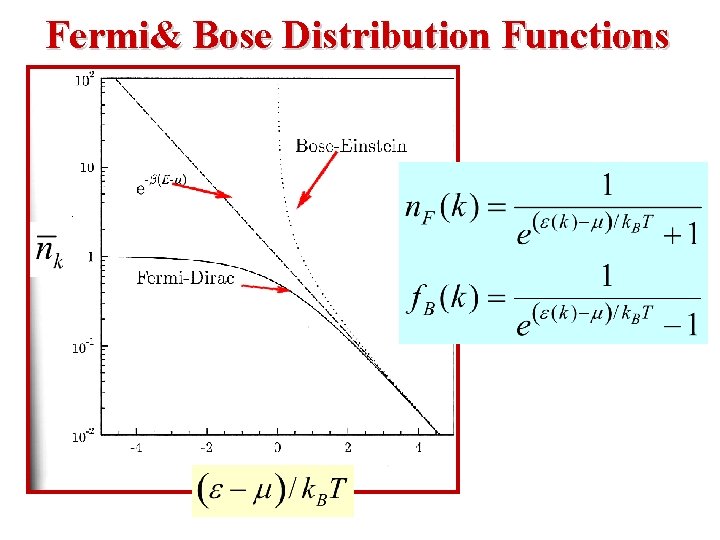
Fermi& Bose Distribution Functions

Fermi-Dirac Distribution Primary Application: Electrons in a Conductor • The Density of States g(E) specifies how many states exist For free electrons, ½ g(E) at a given energy E. • The Fermi Function f(E) specifies how many of the existing states at energy E will be filled with electrons. It is a probability distribution function. Chemical Potential EF = Fermi Energy (Fermi Level)

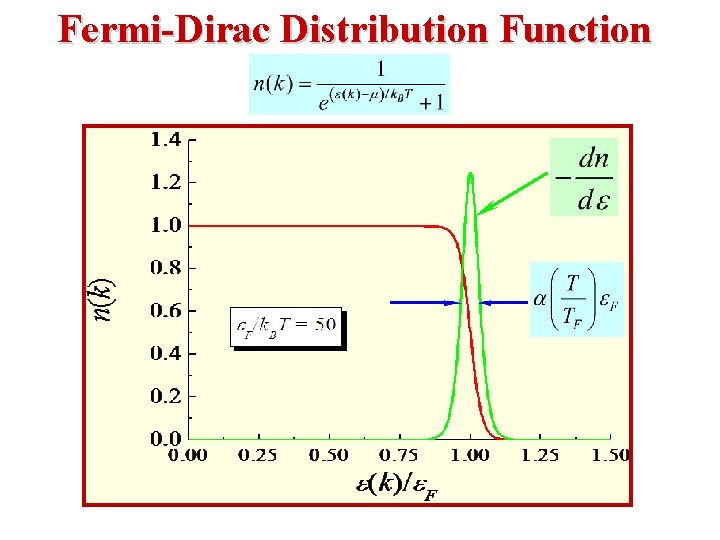
Fermi-Dirac Distribution: Consider the limit as T 0 K For E > EF : For E < EF : E So, as T 0 the Fermi Function l beomes a step function! EF 0 1 f(E)

Fermi-Dirac Statistics EF Fermi Energy • EF is essentially the same as the Chemical Potential μ. Note the following: • At E = EF, the exponential term = 1 & FFD = (½). • As we already said, in the limit as T → 0: • At T = 0, Fermions occupy the lowest energy levels. • Near T = 0, there is only a small probability that a thermal agitation, k. T will kick a Fermion to an energy greater than EF.

Fermi-Dirac Distribution: T > 0 K EF • For common Fermion Systems such as conduction electrons in metals & for T near room temperature, it is ALWAYS true that EF >> k. T (1) • That is, even at room temperature & above, the Fermions are in the “low temperature” limit!

Fermi-Dirac Distribution: T > 0 K • For common Fermion Systems (e. g. conduction electrons in metals) it’s ALWAYS true that EF >> k. T (1) • Consider the case E EF + 3 k. T. • Note that (1) implies that:

Fermi-Dirac Distribution: T > 0 K • This means that for E EF + 3 k. T, a very good approximation to the Fermi Function f(E) is: • That is, for E a few k. T outside of EF, the Fermi Function f(E) is Approximately a MB Distribution!

Fermi-Dirac Distribution: T > 0 K • For common Fermion Systems it is always true that EF >> k. T (1) • Consider the case E EF - 3 k. T. • Note that (1) implies that:

Fermi-Dirac Distribution: T > 0 K • This means that for E EF - 3 k. T, a very good approximation to the Fermi Function f(E) is: • That is, for E a few k. T inside the Fermi Energy EF, the Fermi Function f(E) is Approximately 1 – f. MB (E)!

• From the previous slide, if E EF - 3 k. T, then: • So, approximately • This says that, 1 f(E) (probability that a state is empty inside EF), is very small. That is, most states inside the Fermi Energy EF will be filled. • At room temperature, thermal energy k. T (300 K) = 0. 025 e. V

• So, at ordinary temperatures, most states inside the Fermi Energy EF will be filled. • Room temperature: k. T (300 K) = 0. 025 e. V • For common metals EF 1 to 5 e. V (105 K+) • So At room temperature k. T is very small in comparison with EF • In other words, for ordinary metals at room temperature, the conduction electrons are at “low temperature”!

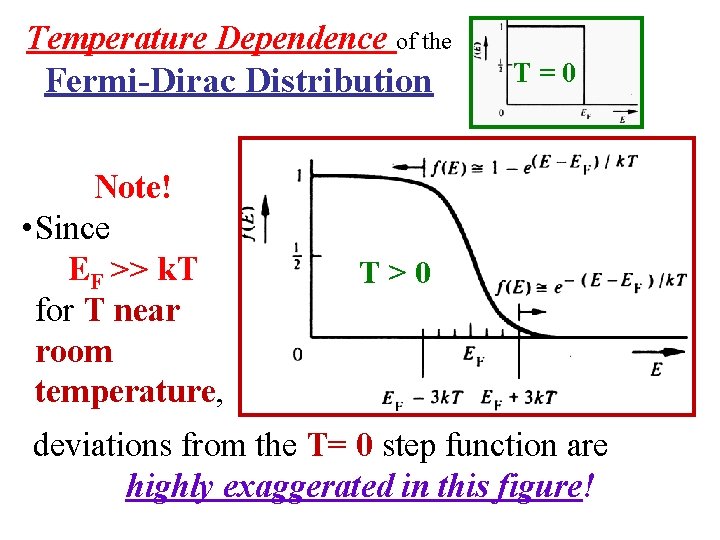
Temperature Dependence of the Fermi-Dirac Distribution Note! • Since EF >> k. T for T near room temperature, T=0 T>0 deviations from the T= 0 step function are highly exaggerated in this figure!

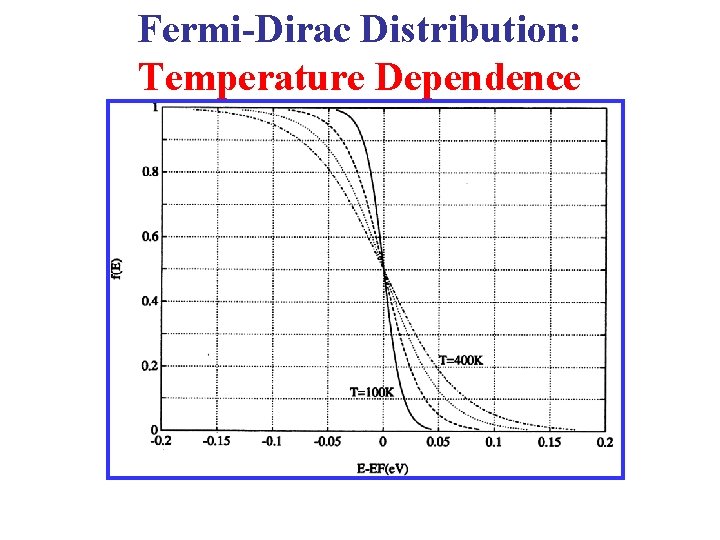
Fermi-Dirac Distribution: Temperature Dependence

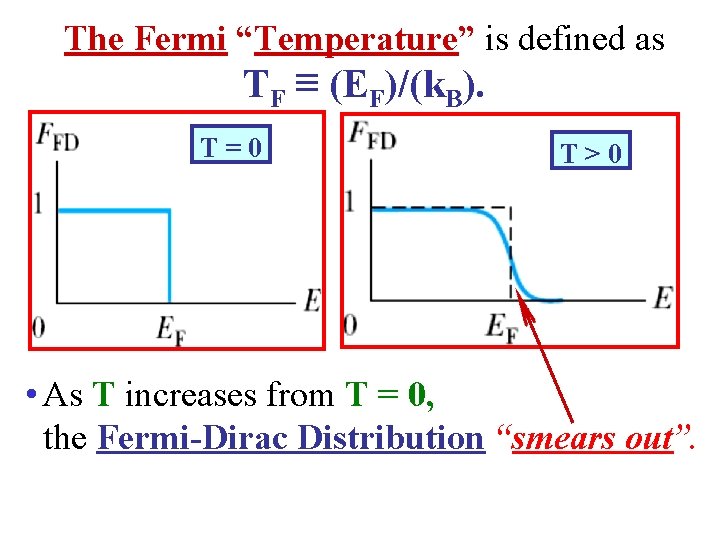
The Fermi “Temperature” is defined as TF ≡ (EF)/(k. B). T=0 T>0 • As T increases from T = 0, the Fermi-Dirac Distribution “smears out”.

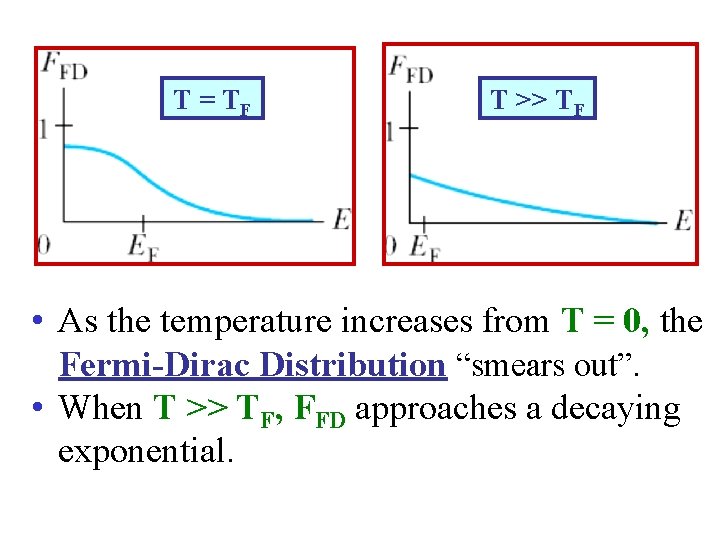
T = TF T >> TF • As the temperature increases from T = 0, the Fermi-Dirac Distribution “smears out”. • When T >> TF, FFD approaches a decaying exponential.

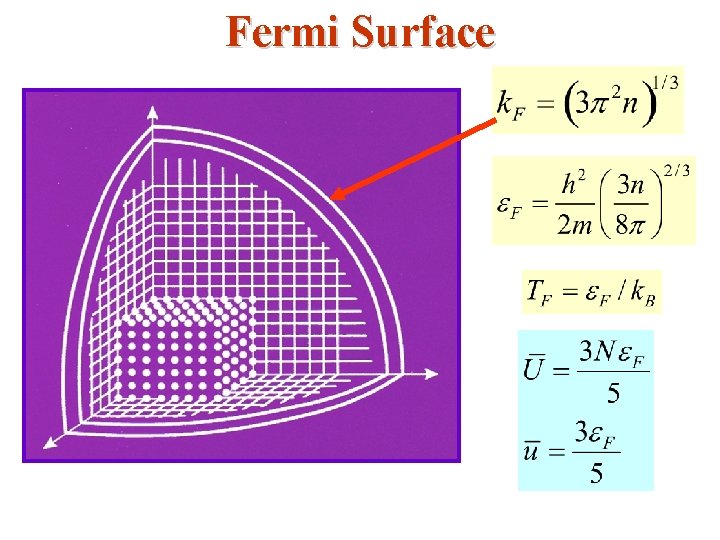
• At T 0 the Fermi Energy EF energy of the highest occupied quantum level. • If there a total of N electrons, then its easy to show (Reif, Ch. 9) that EF has the form:

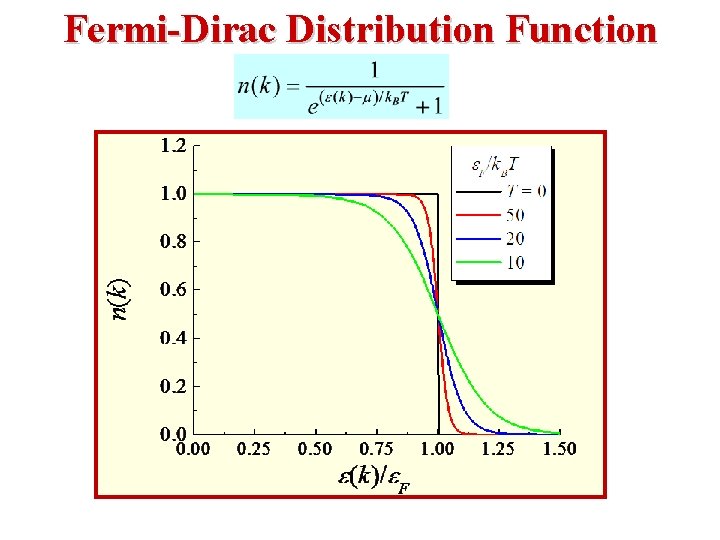
Fermi-Dirac Distribution Function

Fermi-Dirac Distribution Function

Fermi Surface kz kx

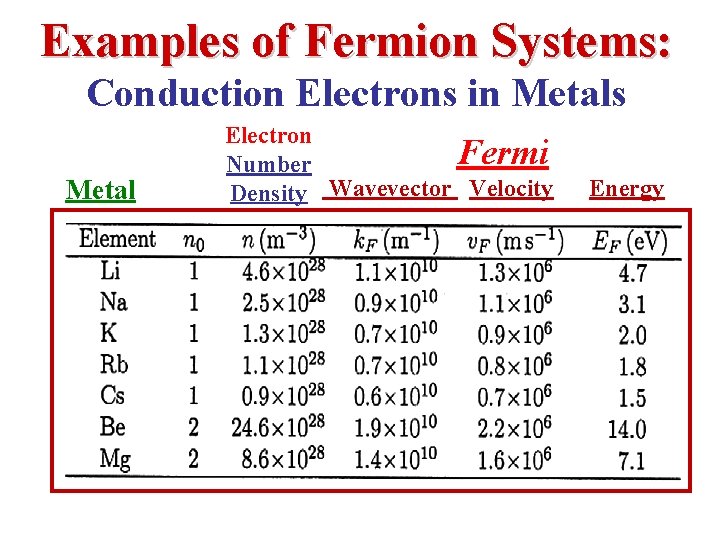
Examples of Fermion Systems: Conduction Electrons in Metals Metal Electron Fermi Number Density Wavevector Velocity Energy

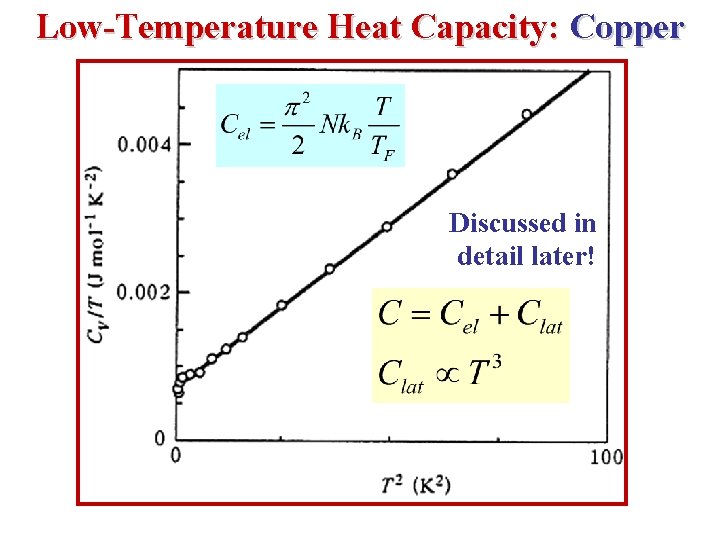
Low-Temperature Heat Capacity: Copper Discussed in detail later!

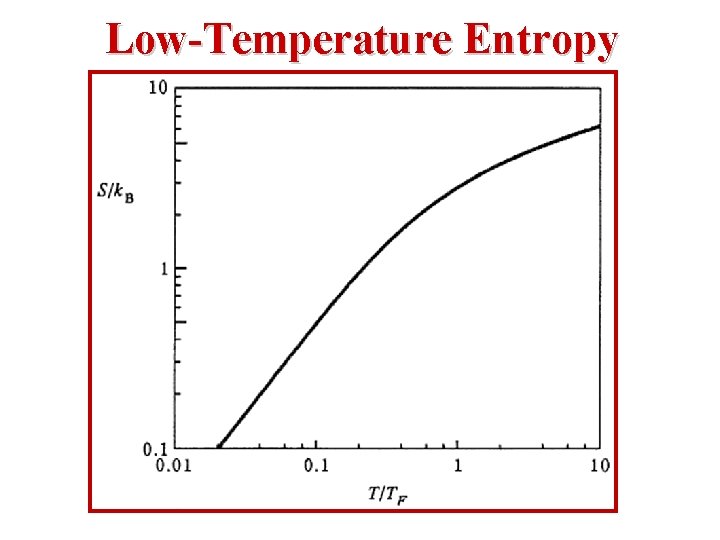
Li ne ar reg im e Low-Temperature Entropy

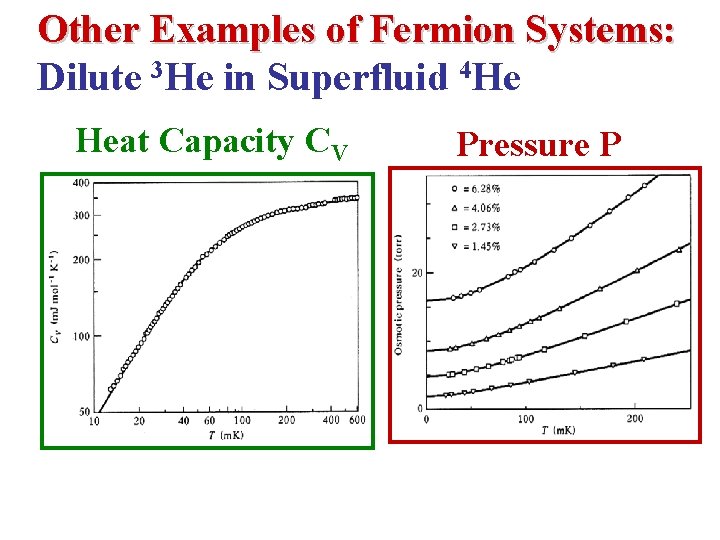
Other Examples of Fermion Systems: Dilute 3 He in Superfluid 4 He Heat Capacity CV Pressure P