Quantum spin Hall effect Shoucheng Zhang Stanford University

Quantum spin Hall effect Shoucheng Zhang (Stanford University) Collaborators: Andrei Bernevig, Congjun Wu (Stanford) Xiaoliang Qi (Tsinghua), Yongshi Wu (Utah) Murakami, Nagaosa (Tokyo) cond-mat/0504147 cond-mat/0505308 cond-mat/0508273 HK meeting, 2005/12

Generalization of the quantum Hall effect • Quantum Hall effect exists in D=2, due to Lorentz force. • Natural generalization to D=3, due to spin-orbit force: • 3 D hole systems (Murakami, Nagaosa and Zhang, Science 2003) • 2 D electron systems (Sinova et al, PRL 2004)

The intrinsic spin Hall effect • Key advantage: • electric field manipulation, rather than magnetic field. • dissipationless response, since both spin current and the electric field are even under time reversal. • Topological origin, due to Berry’s phase in momentum space similar to the QHE. • Contrast between the spin current and the Ohm’s law:

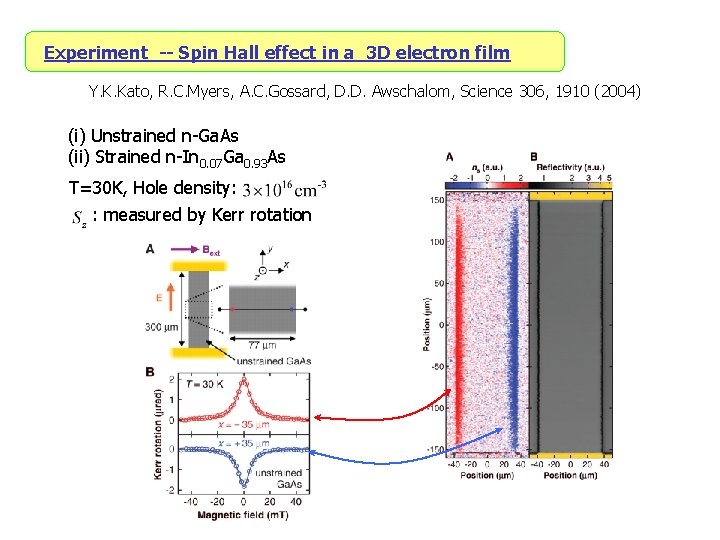
Experiment -- Spin Hall effect in a 3 D electron film Y. K. Kato, R. C. Myers, A. C. Gossard, D. D. Awschalom, Science 306, 1910 (2004) (i) Unstrained n-Ga. As (ii) Strained n-In 0. 07 Ga 0. 93 As T=30 K, Hole density: : measured by Kerr rotation

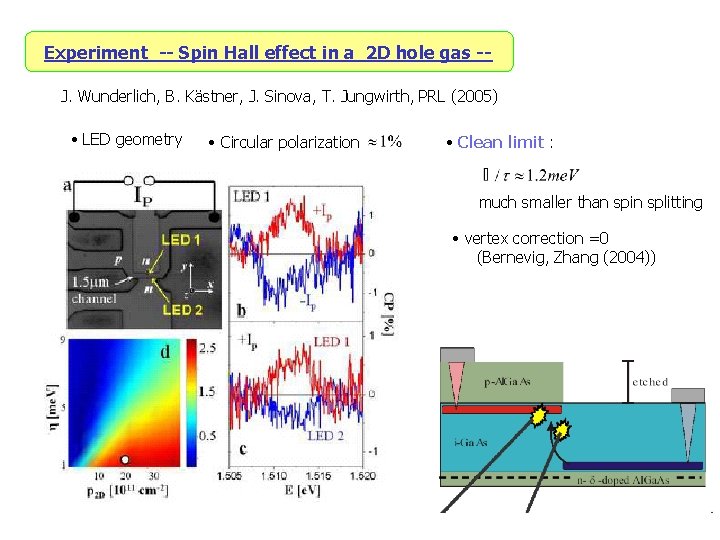
Experiment -- Spin Hall effect in a 2 D hole gas -J. Wunderlich, B. Kästner, J. Sinova, T. Jungwirth, PRL (2005) • LED geometry • Circular polarization • Clean limit : much smaller than spin splitting • vertex correction =0 (Bernevig, Zhang (2004))

• What about the quantum anomalous Hall effect and the quantum spin Hall effect?

Key ingredients of the quantum Hall effect: • Time reversal symmetry breaking. • Bulk gap. • Gapless chiral edge states. • External magnetic field is not necessary! Quantized anomalous Hall effect: • Time reversal symmetry breaking due to ferromagnetic moment. • Topologically non-trivial bulk band gap. • Gapless chiral edge states ensured by the index theorem.

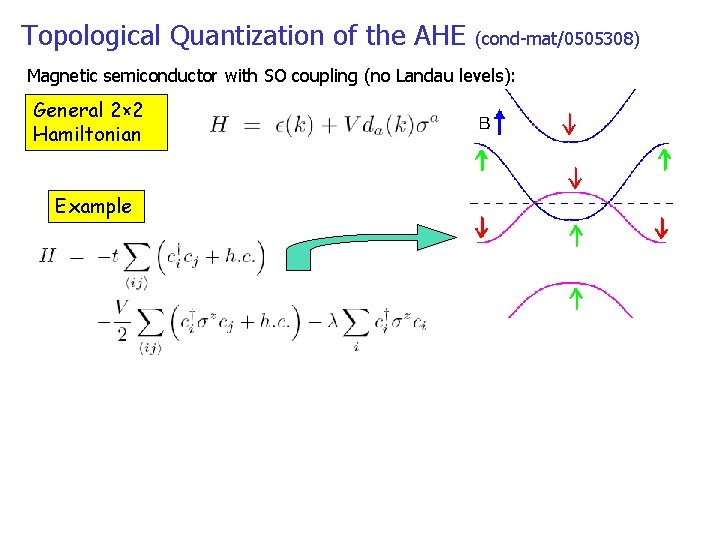
Topological Quantization of the AHE (cond-mat/0505308) Magnetic semiconductor with SO coupling (no Landau levels): General 2× 2 Hamiltonian Example Rashbar Spinorbital Coupling

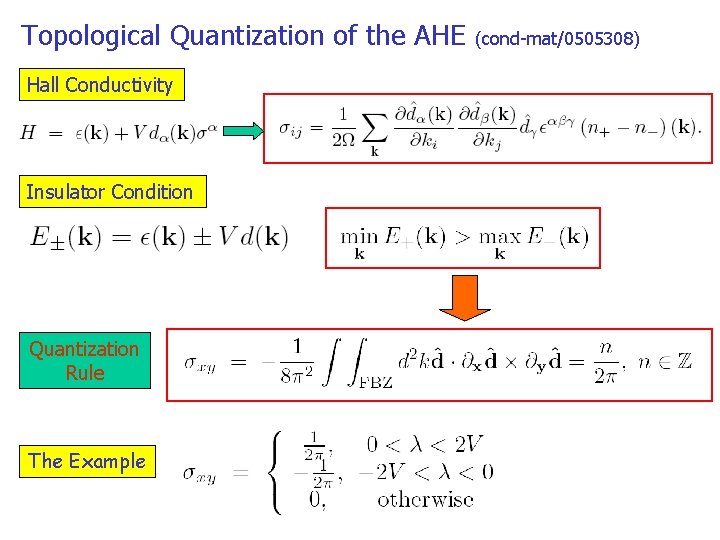
Topological Quantization of the AHE Hall Conductivity Insulator Condition Quantization Rule The Example (cond-mat/0505308)

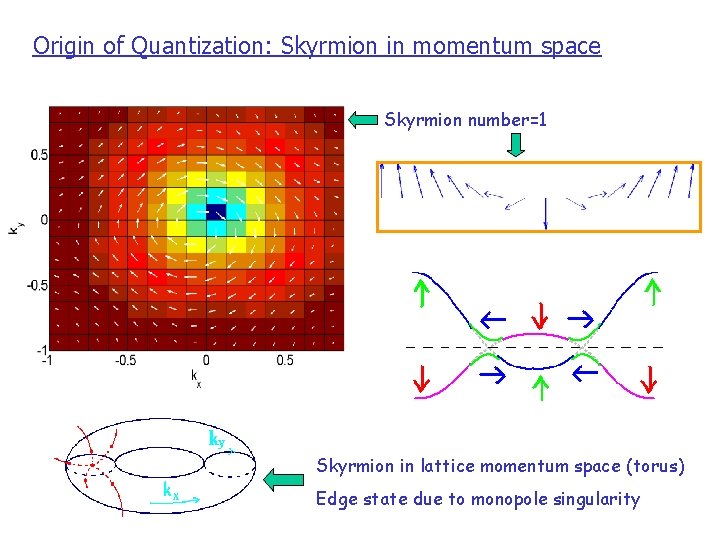
Origin of Quantization: Skyrmion in momentum space Skyrmion number=1 Skyrmion in lattice momentum space (torus) Edge state due to monopole singularity

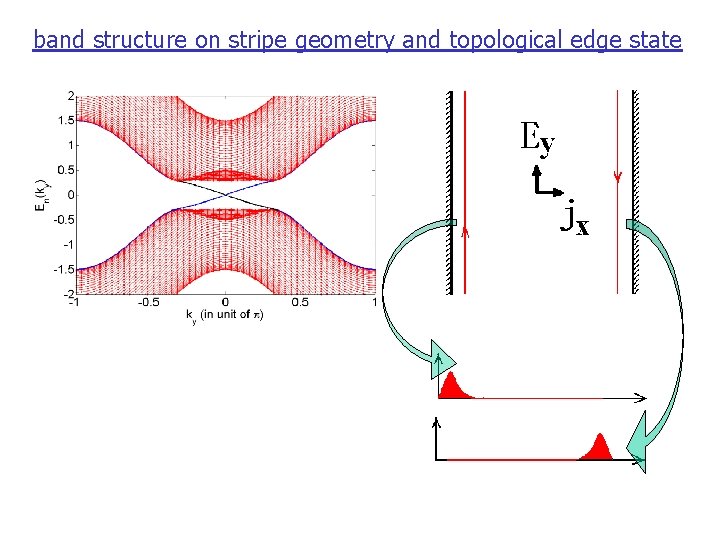
band structure on stripe geometry and topological edge state

Spin-Hall insulator: dissipationless spin transport without charge transport (PRL 93, 156804, 2004) • In zero-gap semiconductors, such as Hg. Te, Pb. Te and a-Sn, the HH band is fully occupied while the LH band is completely empty. • A charge gap can be induced by pressure. In this case, charge conductivity vanishes, but the spin Hall conductivity is maximal.

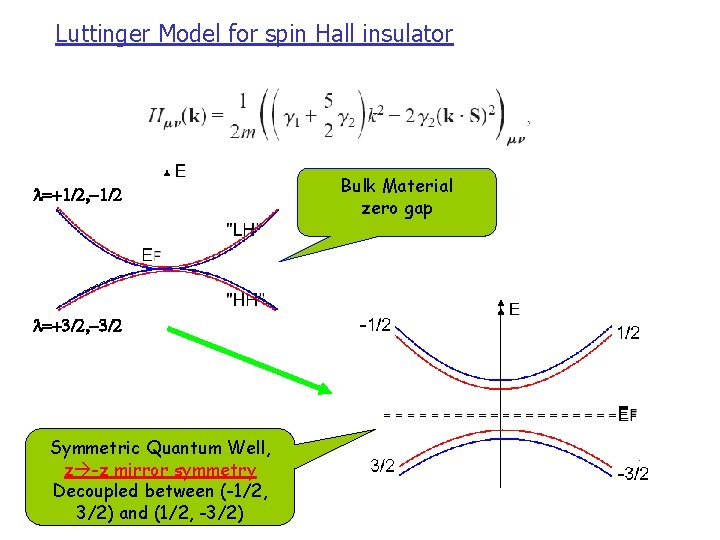
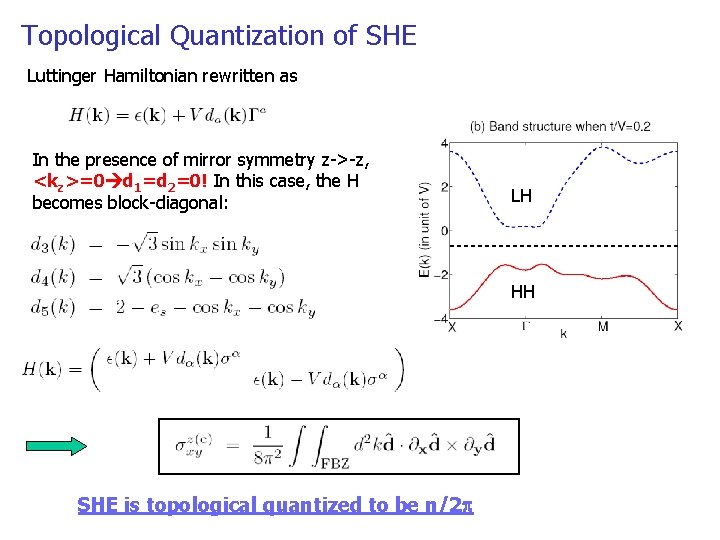
Luttinger Model for spin Hall insulator l=+1/2, -1/2 l=+3/2, -3/2 Symmetric Quantum Well, z -z mirror symmetry Decoupled between (-1/2, 3/2) and (1/2, -3/2) Bulk Material zero gap

Topological Quantization of SHE Luttinger Hamiltonian rewritten as In the presence of mirror symmetry z->-z, <kz>=0 d 1=d 2=0! In this case, the H becomes block-diagonal: LH HH SHE is topological quantized to be n/2 p

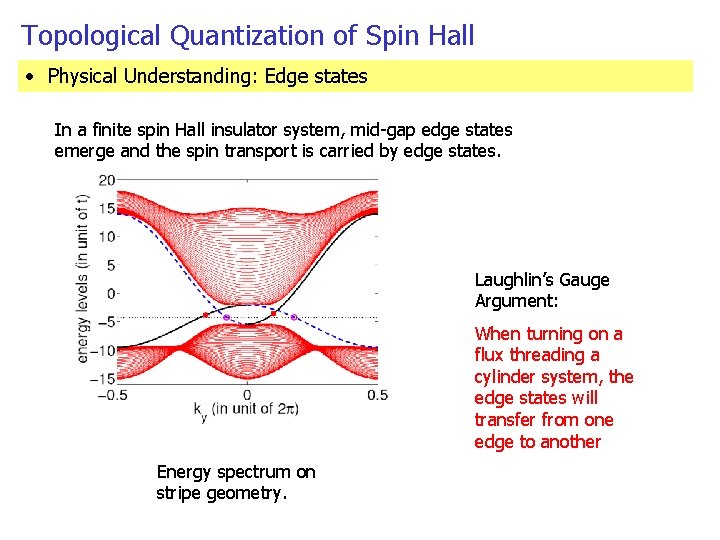
Topological Quantization of Spin Hall • Physical Understanding: Edge states In a finite spin Hall insulator system, mid-gap edge states emerge and the spin transport is carried by edge states. Laughlin’s Gauge Argument: When turning on a flux threading a cylinder system, the edge states will transfer from one edge to another Energy spectrum on stripe geometry.

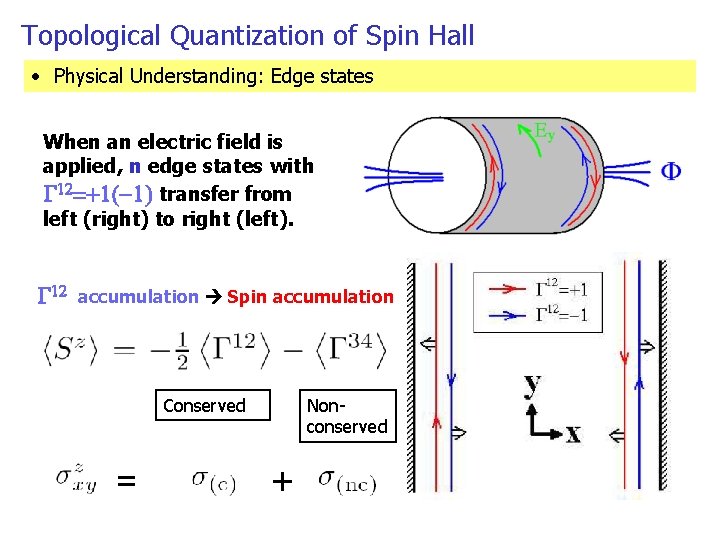
Topological Quantization of Spin Hall • Physical Understanding: Edge states When an electric field is applied, n edge states with G 12=+1(-1) transfer from left (right) to right (left). G 12 accumulation Spin accumulation Conserved = Nonconserved +

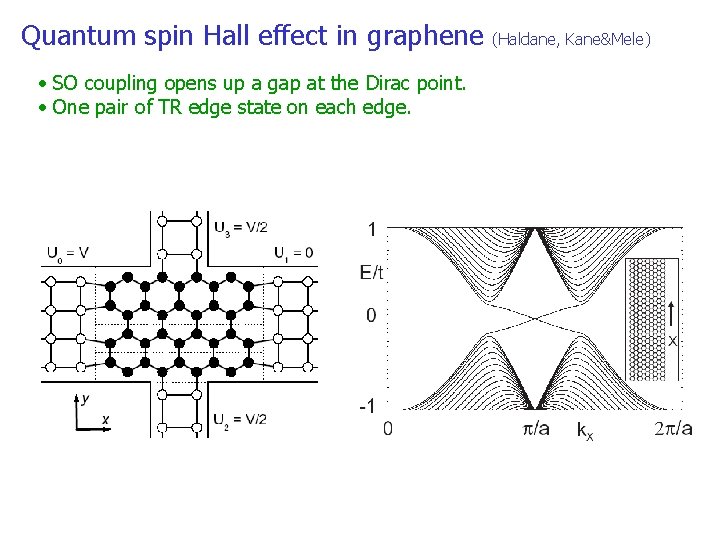
Quantum spin Hall effect in graphene • SO coupling opens up a gap at the Dirac point. • One pair of TR edge state on each edge. (Haldane, Kane&Mele)

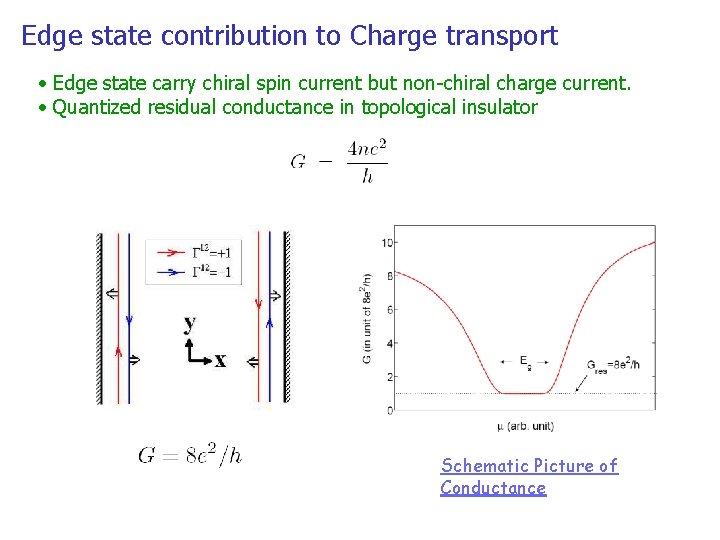
Edge state contribution to Charge transport • Edge state carry chiral spin current but non-chiral charge current. • Quantized residual conductance in topological insulator Schematic Picture of Conductance

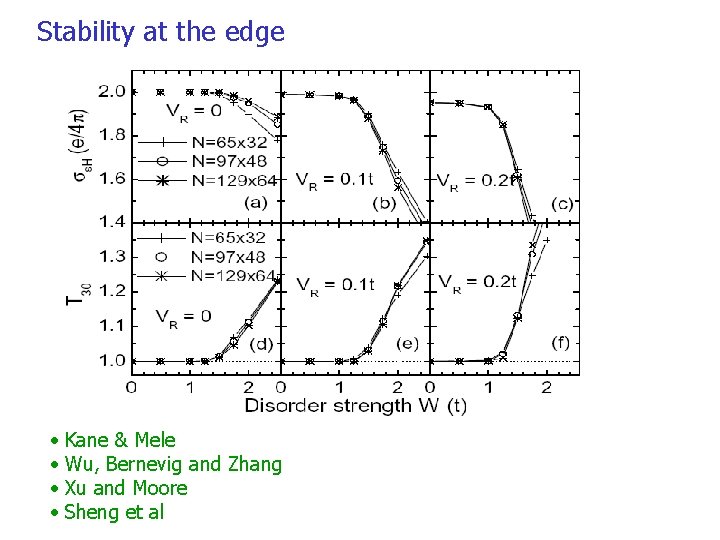
Stability at the edge • The edge states of the QSHE is the 1 D helical liquid. Opposite spins have the opposite chirality at the same edge. • It is different from the 1 D chiral liquid (T breaking), and the 1 D spinless fermions. • T 2=1 for spinless fermions and T 2= -1 for helical liquids. • Single particle backscattering is not possible for helical liquids!

Stability at the edge • Kane & Mele • Wu, Bernevig and Zhang • Xu and Moore • Sheng et al

Conclusion & Discussion • Quantum AHE. • Ferromagnetic insulators with spin-orbit coupling. • Topologically non-trivial band gap. • Hall conductance=Skyrmion number in momentum space. • Number of chiral edge modes=Skyrmion number in momentum space. • Quantum SHE: • Standard semiconductor with a strain gradient, narrow gap semiconductors, and monolayers of graphene. • A new type of 1 D metal: the helical liquid. • Stability ensured by the time reversal symmetry of the spin current.