Quantum Physics Mathematics Quantum Physics Tools in Real

Quantum Physics Mathematics

Quantum Physics Tools in Real Life Reality

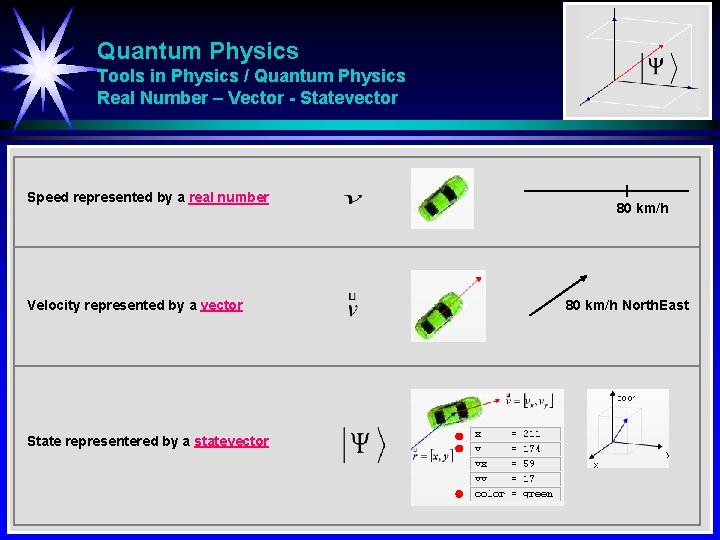
Quantum Physics Tools in Physics / Quantum Physics Real Number – Vector - Statevector Speed represented by a real number Velocity represented by a vector State representered by a statevector 80 km/h North. East

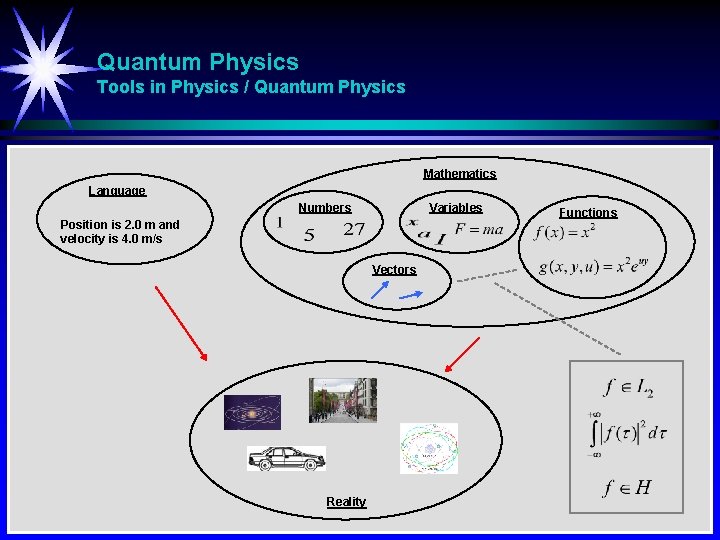
Quantum Physics Tools in Physics / Quantum Physics Mathematics Language Numbers Variables Position is 2. 0 m and velocity is 4. 0 m/s Vectors Reality Functions

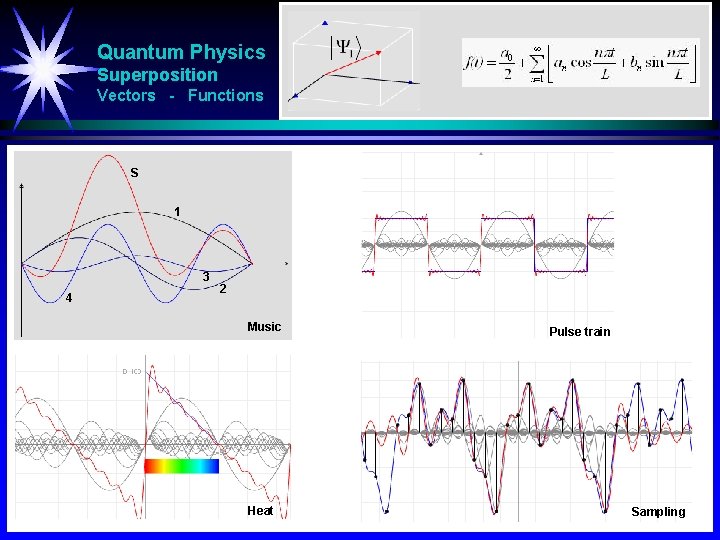
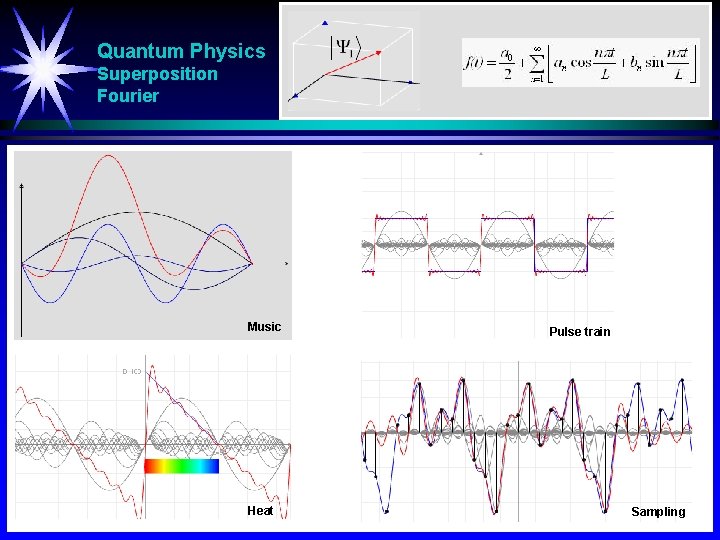
Quantum Physics Superposition Vectors - Functions S 1 3 4 2 Music Heat Pulse train Sampling

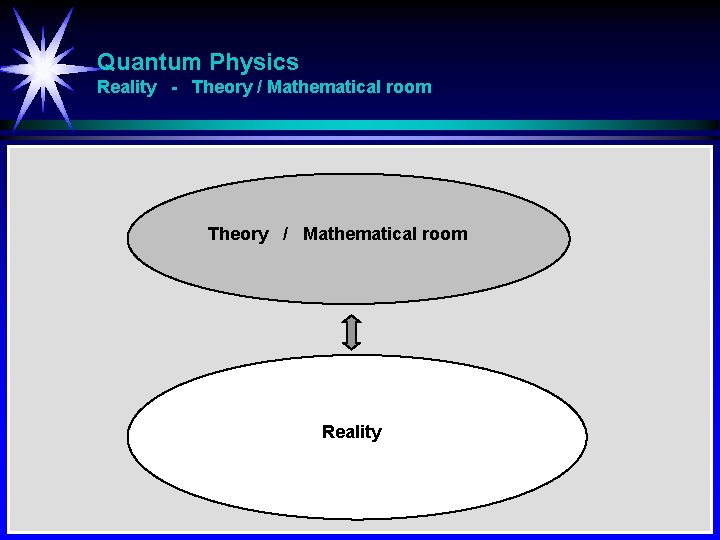
Quantum Physics Reality - Theory / Mathematical room Reality

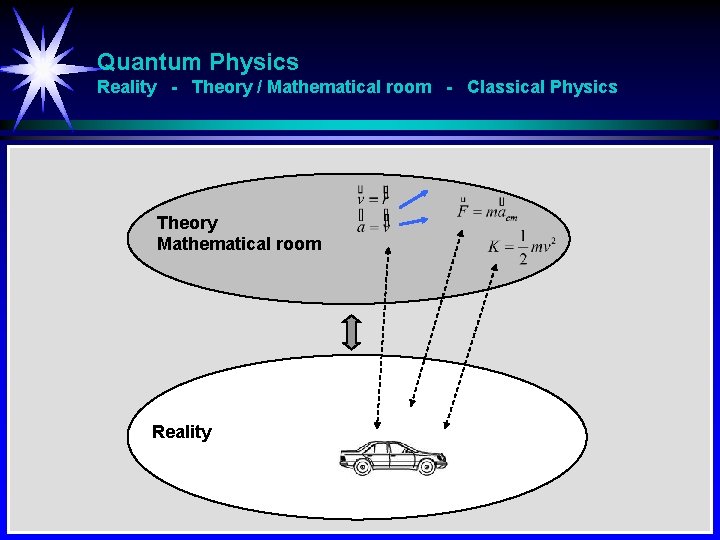
Quantum Physics Reality - Theory / Mathematical room - Classical Physics Theory Mathematical room Reality

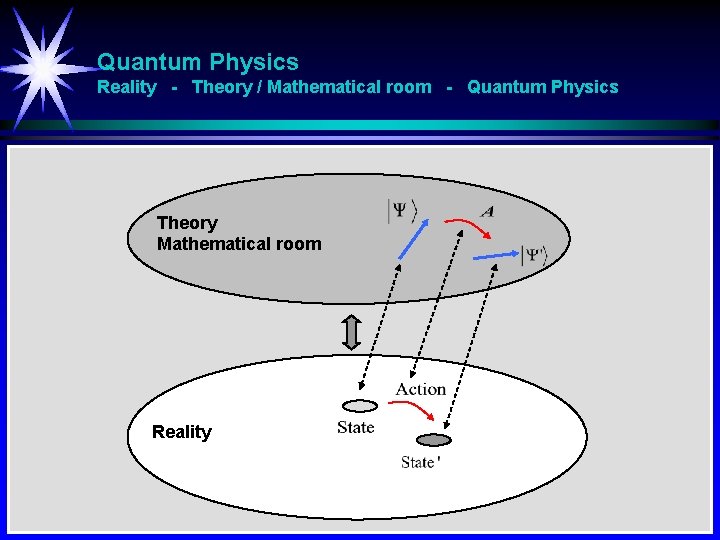
Quantum Physics Reality - Theory / Mathematical room - Quantum Physics Theory Mathematical room Reality

Quantum Physics Postulate 1 1. Every system is described by a state vector that is an element of a Hilbert space.

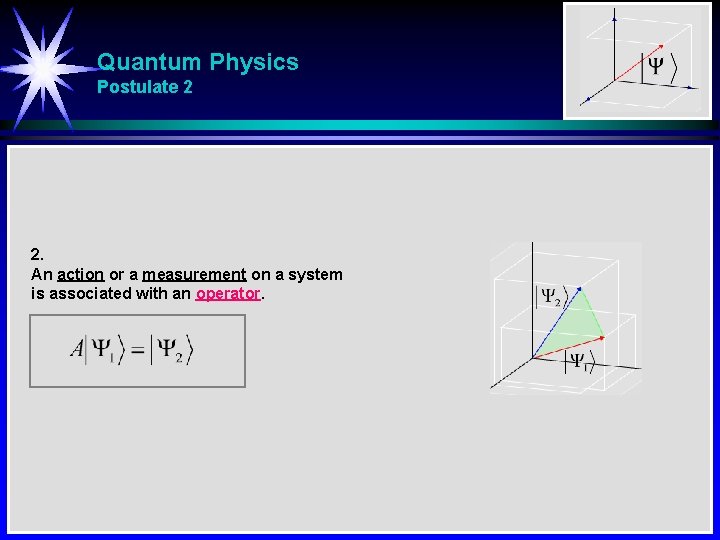
Quantum Physics Postulate 2 2. An action or a measurement on a system is associated with an operator.

Quantum Physics Observation / Measurement in daily life The length of the table is independent of an observation or a measurement. The behaviour of the class is perhaps not independent of an observation (making a video of the class)

Quantum Physics Observation of position, changing the velocity A ball with a known velocity and unknown position. Try to determine the position. A bit unlucky one foot hits the ball. The position is known when the ball is touched, but now the velocity is changing. Just after the hit of the ball, the position is known, but now the velocity is unknown.

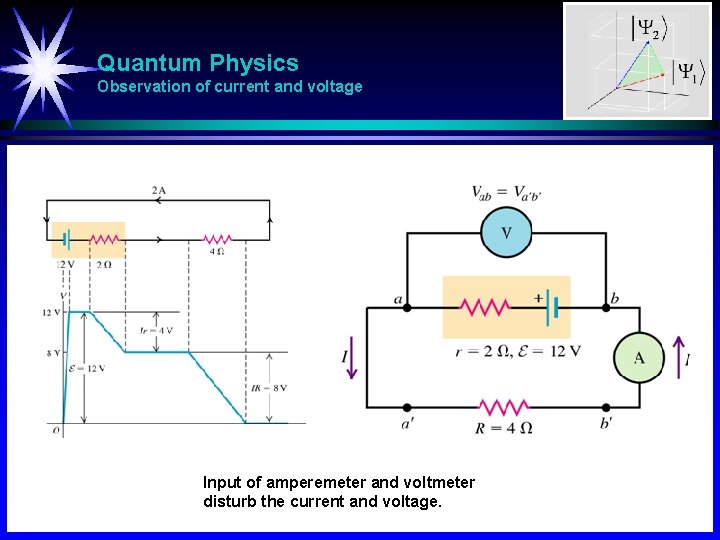
Quantum Physics Observation of current and voltage Input of amperemeter and voltmeter disturb the current and voltage.

Quantum Physics Stern-Gerlach experiment [1/2] Observation of angular momentum in one direction influence on the angular momentum in another direction V 1 Silver atoms going through a vertical magnetic field dividing the beam into two new beams dependent of the angular momentum of the atom. B 1 B B 2 V 1 B Three magnetic fields: Vertical, horizontal, vertical. Every time the beam is divided into two new beams. H 1 B 1 B 2 B 121 No sorting mechanism. A new vertical/horisontal measurement B 122 disturbs/changes the horisontal/vertical beam property.

Quantum Physics Stern-Gerlach experiment [2/2] Observation of angular momentum in one direction influence on the angular momentum in another direction 1 2 3 B B B S-G z-axis z+ z- z+ S-G z-axis No z- x+ S-G x-axis x- x+ x- S-G z-axis z+ z-

Quantum Physics Entanglement Quantum entanglement occurs when particles such as photons, electrons, molecules and even small diamonds interact physically and then become separated. When a measurement is made on one of member of such a pair, the other member will at any subsequent time be found to have taken the appropriate correlated value. According to the Copenhagen interpretation of quantum physics, their shared state is indefinite until measured. Entanglement is a challange in our understanding of nature og will hopefully give us new technological applications.

Quantum Physics Observation / Measurement - Classical A car (particle) is placed behind a person. The person with the car behind, cannot see the car. The person turns around and observeres the car. Classically we will say: The car was at the same place also just before the observation.

Quantum Physics Observation / Measurement - Quantum A A car is placed in the position A behind a person. The person with the car behind, cannot yet observe the car. B The person turns around and observeres the car in the position B. In quantum physics it’s possible that the observation of a property of the car moves the car to another position.

Quantum Physics Observation / Measurement - Quantum Question: Where was the car before the observation? ? Realist: The car was at B. Orthodox: The car wasn’t really anywhere. B Agnostic: Refuse to answer. If this is true, quantum physics is incomplete. There must be some hidden variables (Einstein). It’s the act of measurement that force the particle to ‘take a stand’. Observations not only disturb, but they also produce. No sense to ask before a measurent. Orthodox supported by theory (Bell 1964) and experiment (Aspect 1982).

Quantum Physics Observation Before the measurement M After the measurement M

M Quantum Physics Observation Superposition Before the measurement the position of the car is a superposition of infinitely many positions. M The measurement produce a specific position of the car. M A repeated measurement on the new system produce the same result. M

Quantum Physics Superposition Fourier Music Heat Pulse train Sampling

Quantum Physics Classical: Vector expanded in an orthonormal basis - I

Quantum Physics Classical: Vector expanded in an orthonormal basis - II Complex coefficients

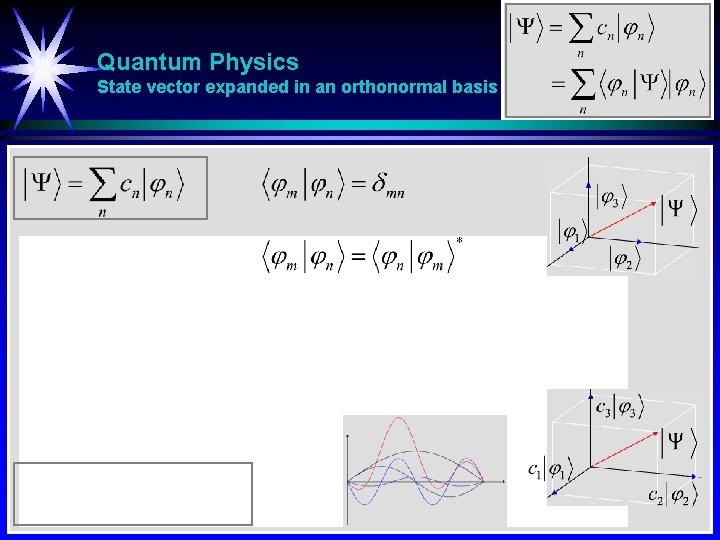
Quantum Physics State vector expanded in an orthonormal basis

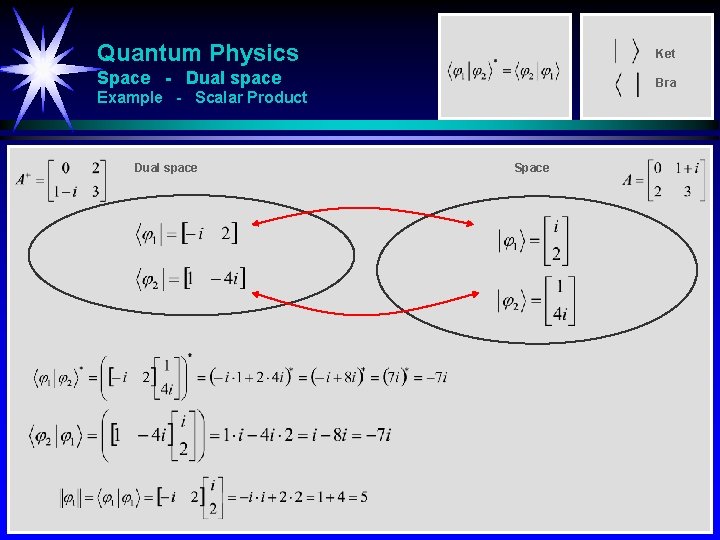
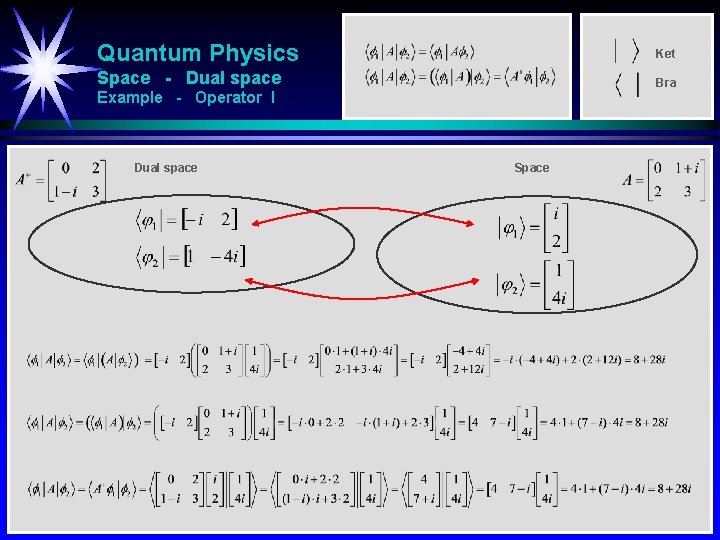
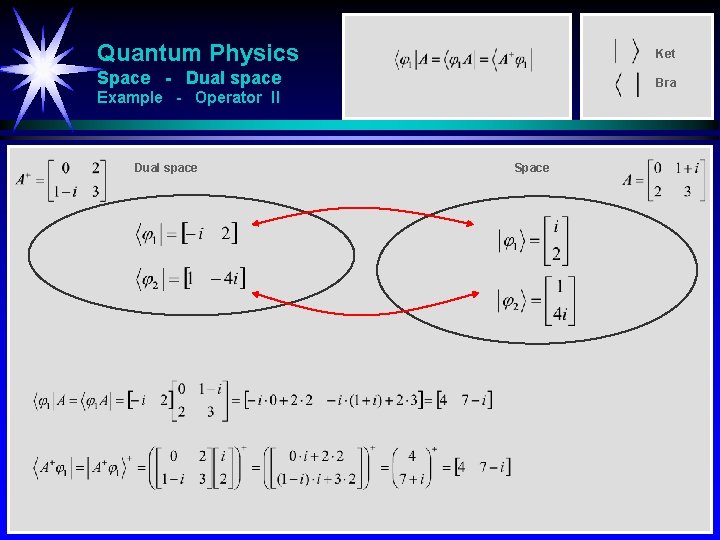
Quantum Physics Ket Space - Dual space Bra Introduction Dual space The object is defined to the bra that acting on the ket Space gives the number

Quantum Physics Ket Space - Dual space Bra Example - Real Elements Dual space Space

Quantum Physics Bra Ket Space - Dual space Ket Bra Example - Complex Elements Dual space Space

Quantum Physics Ket Space - Dual space Bra Example - Scalar Product Dual space Space

Quantum Physics Ket Space - Dual space Bra Example - Operator I Dual space Space

Quantum Physics Ket Space - Dual space Bra Example - Operator II Dual space Space

Quantum Physics Ket Space - Dual space Bra Example - Operator II Dual space Space

Quantum Physics Ket Space - Dual space Bra Example - Operator III Dual space Space

Quantum Physics Probability amplitude Same state cn cn 2 : Probability amplitude : Probability Normalization of a state vector don’t change the probability distributions. Therefore we postulate c and to represent the same state.

Quantum Physics Projection Operator Theory

Quantum Physics Projection Operator Example - Projection to basisfunction

Quantum Physics Projection Operator Example - Projection to subroom

Quantum Physics Unit Operator Theory

Quantum Physics Unit Operator Example

Quantum Physics Orthonormality - Completeness Orthonormality Projection Operator Completeness

Quantum Physics Orthonormality - Completeness Discrete - Continuous Discrete State Orthonormality Projection Operator Completeness Continuous

Quantum Physics Operator Eigenvectors - Eigenvalues Eigenvectors are of special interest since experimentally we always observe that subsequent measurements of a system return the same result (collapse of wave function). A A Consequence of Spectral Theorem: The only allowed physical results of measurements of the observable A are the elements of the spectrum of the operator which corresponds to A. Measured quantity

Quantum Physics Operator Self-adjoint operator Def: Self-adjoint operator: Def: Hermitian operator: The distinction between Hermitian and self-adjoint operators is relevant only for operators in infinite-dimensional vector spaces. Proof:

Quantum Physics Operator Theorem: Proof: Canceling i and adding

Quantum Physics Hermitian operator The eigenvalues of a Hermitian operator are real Theorem: Proof: The eigenvalues of a Hermitian operator are real.

Quantum Physics Hermitian operator Eigenstates with different eigenvalues are orthogonal Theorem: Proof: Eigenstates corresponding to distinct eigenvalues of an Hermitian operator must be orthogonal.

Quantum Physics Operator expanded by eigenvectors Eigenvectors are of special interest since experimentally we always observe that subsequent measurements of a system return the same result (collapse of wave function) The measurable quantity is associated with the eigenvalue. This eigenvalue should be real so A have to be a self-adjoint operator A+ = A Every operator can be expanded by their eigenvectors and eigenvalues

Quantum Physics Average of Operator [1/2]

Quantum Physics Average of Operator [2/2]

Quantum Physics Determiate state Determinate state: A state prepared so a measurement of operator A is certain to return the same value a every time. Unless the state is an eigenstate of the actual operator, we can never predict the result of the operator only the probability. The determinate state of the operator A that return the same value a every time is the eigenstate of A with the eigenvalue a.

Quantum Physics Uncertainty [1/3]

Quantum Physics Uncertainty [2/3]

Quantum Physics Uncertainty [3/3]

Quantum Physics Kinematics and dynamics Necessary with correspondence rules that identify variables with operators. This can be done by studying special symmetries and transformations. The laws of nature are believed to be invariant under certain space-time symmetry operations, including displacements, rotations, and transformations between frames of reference. Corresponding to each such space-time transformation there must be a transformation of observables, opetators and states. Energy, linear and angular momentum are closely related to space-time symmetry transformations. Operator Variable

Quantum Physics Noether’s theorem Noether’s (first) theorem states that any differentiable symmetry of the action (law) of a physical system has a corresponding conservation law. Symmetry Conservation Time translation Space translation Rotation Energy Linear momentum Angular momentum E p L

Quantum Physics Invariant transformation Unitary operator The laws of nature are believed to be invariant under certain space-time symmetry. Therefore we are looking for a continous transformation that are preservering the probability distribution. Any mapping of the vector space onto itself that preserves the value of |< | >| may be implemented by an operator U being either unitary (linear) or antiunitary (antilinear). Only linear operators can describe continous transformations.

Quantum Physics Unitary operator Any mapping of the vector space onto itself that preserves the value of |< | >| may be implemented by an operator U being ether unitary (linear) or antiunitary (antilinear). Only linear operators can describe continous transformations.

Quantum Physics Generator of infinitesimal transformation Any mapping of the vector space onto itself that preserves the value of |< | >| may be implemented by an operator U being ether unitary (linear) or antiunitary (antilinear). Only linear operators can describe continous transformations.

Quantum Physics Time operator - Time dependent Schrödinger equation Energy operator - Generator for time displacement Energy operator Generator for time displacement

Quantum Physics Schrödinger Equation Time dependent / Time independent Time dependent Schrödinger equation Time independent potensial Time independent probability

Quantum Physics Schrödinger equation - Time independent Stationary states

Quantum Physics Normalization is time-independent

Quantum Physics Moment operator in position space

Quantum Physics Schrödinger equation - Time independent

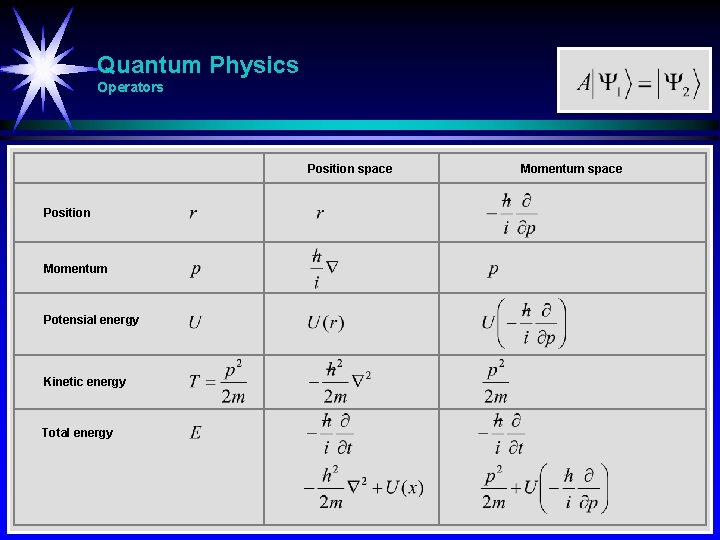
Quantum Physics Operators Position space Position Momentum Potensial energy Kinetic energy Total energy Momentum space

Quantum Physics Uncertainty Position / Momentum - Energy / Time Position Momentum Energy Time