Quantum Physics MachZehnder Quantum Physics MachZehnder Interferometer Info

Quantum Physics Mach-Zehnder

Quantum Physics Mach-Zehnder Interferometer Info State 1 State 0 P P Beam splitter State 1 A P Quantum Particle Two possible states: 1 or 0 (polarization, spin, …) P Detection of the state by a beam splitter B P State 0 Illustrates the two possible instates by two different inpath A and B

Quantum Physics Mach-Zehnder Interferometer Double Beam Splitter P S 1 – S 4 S 2 – S 3 Y p 34 X S 3 A particle P is coming in path A or B. S 4 p 13 P p 24 S 1 S 2 A B p 12 Particle Half-silvered mirror Fully silvered mirror At the half-silvered mirror S 1 it’s 50/50 percent chance that the particle will go through the mirror and travel the path p 12 or be reflected and travel the path p 13. The mirrors S 2 and S 3 are fully silvered so the particle is reflected and travel the path p 24 or p 34. At the half-silvered mirror S 4 it’s 50/50 percent chance that the particle will go through the mirror or be reflected and travel the path X or Y.

Quantum Physics Mach-Zehnder Interferometer Classical Particle An experiment with a classical particle P. Y At the moment we have the following situation: p 34 19 particles have travelled the path p 12 – p 24. 18 particles have travelled the path p 13 – p 34. X P p 13 17 particles have travelled the path X. 19 particles have travelled the path Y. p 24 Ordinary statistical theory tells us that there will be 50/50 percent of particles travelling the path p 12 - p 24 or p 13 - p 34. There will be 50/50 percent of particles travelling the path X or Y. A B p 12 0. 5 A p 13 0. 5 0. 25 X 0. 5 0. 25 Y 0. 5 0. 25 X 0. 25 Y

Quantum Physics Mach-Zehnder Interferometer Quantum Particle - Result An experiment with a quantum particle P. Y At the moment we have the following situation: P X 34 particles have been travelling out the path X. 0 particles have been travelling out the path Y. Quantum theory tells us the following: If the quantum particle is starting in the path A, then every particle will be travelling the out-path X. If the quantum particle is staring in the path B, then every particle will be travelling the out-path Y. A P B This result is very surprising compared to classical physics. How to explain this?

Quantum Physics Mach-Zehnder Interferometer Quantum Particle - Measurement An experiment with a quantum particle P. Y P X Now we have a measuring instrument to detect which path the quantum particle is travelling. At the moment we have the following situation: 22 particles have been travelling the out-path X. 22 particles have been travelling the out-path Y. Quantum theory tells us the following: A B Measuring instrument How to explain this? If we have a measuring instrument (either in only one or both path) to detect which path the quantum particle is travelling, then the detection ’disturbs’ the quantum effect in such a way that now we will have an equal number of particles travelling in path X or Y.

Quantum Physics Mach-Zehnder Interferometer Quantum Particle - Two orthonormal states An experiment with a quantum particle P. There are two possible initial states u 1 and u 2 for the particle P dependent of the in-path A or B. Let these two possible instates be: A: u 1 = [1, 0] B: u 2 = [0, 1] These two states are orthonormal. P A B

Quantum Physics Mach-Zehnder Interferometer Quantum Particle - Path A - State after 1 beam splitter An experiment with a quantum particle P. The particle P starts in the state u 1. The beam splitter is represented mathematically by an operator called the Hadamard matrix. Operator Hadamard matrix After the beam splitter (mirror) we have equal probability to measure the particle either in the state u 1 or state u 2. The Hadamard matrix (operator) is shown in the figure.

Quantum Physics Mach-Zehnder Interferometer Quantum Particle - Path A - State after 1 beam splitter - Reality / Mathematical Space Reality Mathematical Space P P P

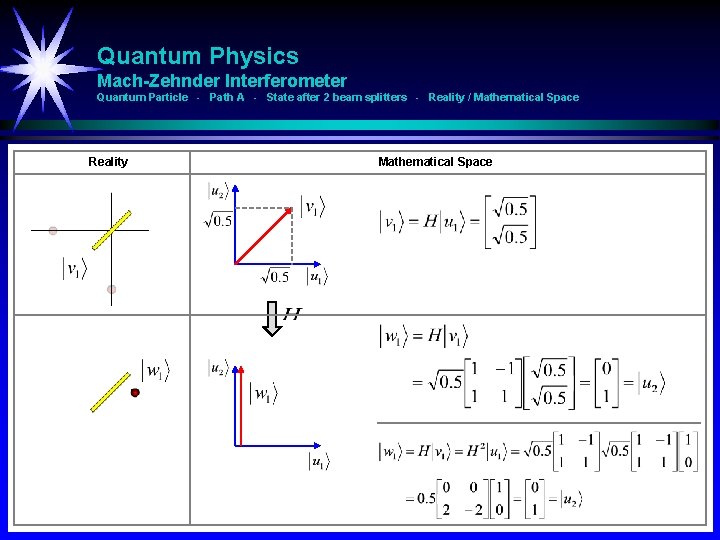
Quantum Physics Mach-Zehnder Interferometer Quantum Particle - Path A - State after 2 beam splitters An experiment with a quantum particle P. Y P P X Operator Hadamard matrix P A B The particle P starts in the state u 1. The beam splitter is represented mathematically by an operator called the Hadamard matrix. After the beam splitter (mirror) we have equal probability to measure the particle either in the state u 1 or state u 2. The Hadamard matrix (operator) is shown in the figure.

Quantum Physics Mach-Zehnder Interferometer Quantum Particle - Path A - State after 2 beam splitters - Reality / Mathematical Space Reality Mathematical Space

Quantum Physics Mach-Zehnder Interferometer Quantum Particle - Path B - State after 1 beam splitter An experiment with a quantum particle P. The particle P starts in the state u 2. The beam splitter is represented mathematically by an operator called the Hadamard matrix. Operator Hadamard matrix A B After the beam splitter (mirror) we have equal probability to measure the particle either in the state u 1 or state u 2. The Hadamard matrix (operator) is shown in the figure.

Quantum Physics Mach-Zehnder Interferometer Quantum Particle - Path B - State after 1 beam splitter - Reality / Mathematical Space Reality Mathematical Space P P P

Quantum Physics Mach-Zehnder Interferometer Quantum Particle - Path B - State after 2 beam splitters An experiment with a quantum particle P. Y P P X Operator Hadamard matrix P A B The particle P starts in the state u 1. The beam splitter is represented mathematically by an operator called the Hadamard matrix. After the beam splitter (mirror) we have equal probability to measure the particle either in the state u 1 or state u 2. The Hadamard matrix (operator) is shown in the figure.

Quantum Physics Mach-Zehnder Interferometer Quantum Particle - State B - State after 2 beam splitters - Reality / Mathematical Space Reality Mathematical Space

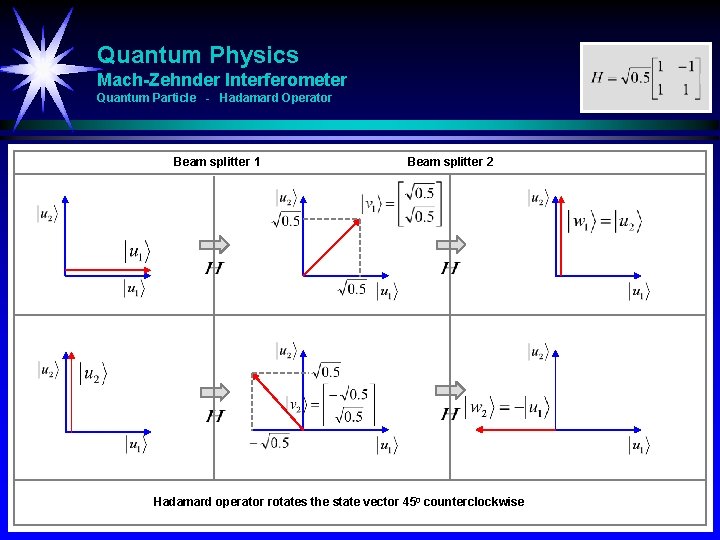
Quantum Physics Mach-Zehnder Interferometer Quantum Particle - Hadamard Operator Beam splitter 1 Beam splitter 2 Hadamard operator rotates the state vector 450 counterclockwise

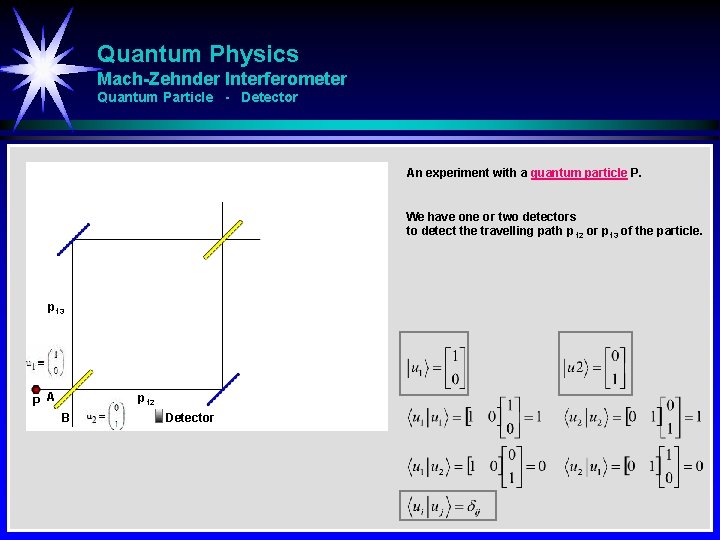
Quantum Physics Mach-Zehnder Interferometer Quantum Particle - Detector An experiment with a quantum particle P. We have one or two detectors to detect the travelling path p 12 or p 13 of the particle. p 13 P A p 12 B Detector

Quantum Physics Mach-Zehnder Interferometer Quantum Particle - State A - Approaching the detector(s) An experiment with a quantum particle P. The particle P starts in the state u 1. The beam splitter is represented mathematically by an operator called the Hadamard matrix. Operator Hadamard matrix p 13 A p 12 B Detector After the beam splitter (mirror) we have equal probability to detect the particle either in the path p 12 or p 13. The particle is approaching the detector(s).

Quantum Physics Mach-Zehnder Interferometer Quantum Particle - State A - Particle is detected in path p 12 An experiment with a quantum particle P. The particle P starts in the state u 1. The beam splitter is represented mathematically by an operator called the Hadamard matrix. p 34 p 13 A p 24 p 12 B Detector After the beam splitter (mirror) we have equal probability to detect the particle in the path p 12 or p|3. Now the particle is detected in the path p 12. The detection of the particle force the particle into one of the eigenstates (here u 2) of the detection operator P.

Quantum Physics Mach-Zehnder Interferometer Quantum Particle - State A - Particle deteced in path p 12 approaching beam splitter S 2 An experiment with a quantum particle P. The particle P starts in the state u 1. The beam splitter is represented mathematically by an operator called the Hadamard matrix. p 34 p 13 A p 24 p 12 B Detector After the beam splitter (mirror) we have equal probability to measure the particle either in the path p 12 or path 13. The detector has detected the particle in path p 12. The particle is now in state u 2 and approaches the second beam splitter S 4.

Quantum Physics Mach-Zehnder Interferometer Quantum Particle - State A - Particle detected in path p 12 passing beam splitter S 4 An experiment with a quantum particle P. Y p 34 X p 13 A p 24 p 12 B Detector The particle P starts in the state u 1. The beam splitter is represented mathematically by an operator called the Hadamard matrix. After the beam splitter (mirror) we have equal probability to measure The particle has been detected in path p 12 and forced into state u 2. After passing the second beam splitter it’s equalt probability to detect the particle in path X or path Y.

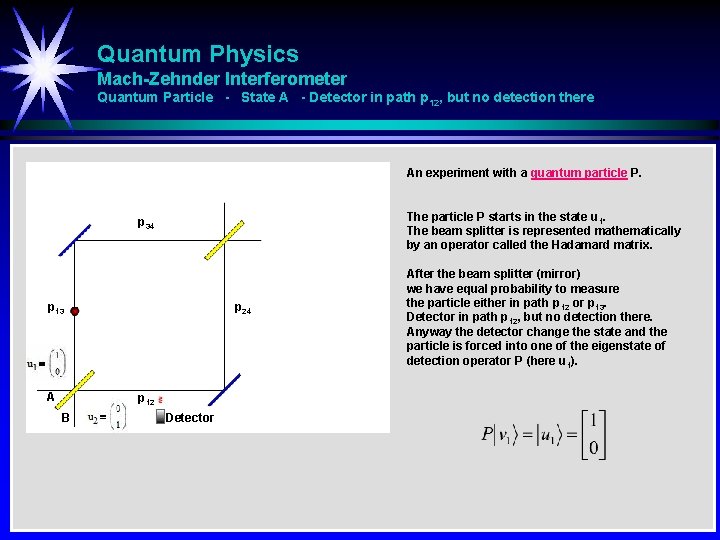
Quantum Physics Mach-Zehnder Interferometer Quantum Particle - State A - Detector in path p 12, but no detection there An experiment with a quantum particle P. The particle P starts in the state u 1. The beam splitter is represented mathematically by an operator called the Hadamard matrix. p 34 p 13 A p 24 p 12 B Detector After the beam splitter (mirror) we have equal probability to measure the particle either in path p 12 or p 13. Detector in path p 12, but no detection there. Anyway the detector change the state and the particle is forced into one of the eigenstate of detection operator P (here u 1).

Quantum Physics Mach-Zehnder Interferometer Quantum Particle - State A - Detector in path p 12 , no detection there - Approaching beam splitter S 4 An experiment with a quantum particle P. P The particle P starts in the state u 1. The beam splitter is represented mathematically by an operator called the Hadamard matrix. After the beam splitter (mirror) we have equal probability to measure the particle either in path p 12 or p 13. Detector in path p 12, but no detection there. Anyway the detector change the state and the particle is forced into one of the eigenstate of detection operator P (here u 1). The particle is approaching the second beam splitter S 4. A B Detector

Quantum Physics Mach-Zehnder Interferometer Quantum Particle - State A - Detector in path p 12, no detection there - Passing beam splitter S 4 An experiment with a quantum particle P. Y X The particle P starts in the state u 1. The beam splitter is represented mathematically by an operator called the Hadamard matrix. After the beam splitter (mirror) we have equal probability to measure the particle either in the path p 12 or p 13. Detector in path p 12, but no detection there. Particle is forced in into state u 1 and equal probability in path X og Y after second beam splitter. A B Detector

Quantum Physics Mach-Zehnder Interferometer Quantum Particle - State A - Approaching the detector(s) An experiment with a quantum particle P. The particle P starts in the state u 1 or u 2. The beam splitter is represented mathematically by an operator called the Hadamard matrix. Operator Hadamard matrix p 13 A After the beam splitter (mirror) we have equal probability to measure the particle either in the state u 1 or state u 2. The particle is approaching the detector(s). p 12 B Detector There is no possibility to decide if the particle is coming from A or B using a detector in the path p 12 or p 13 after the first beam splitter S 1. We have to let the particle be undisturbed until passing the second beam splitter S 4. Equal probability for detecting particle in path p 12 or p 13 independent of particle in-path A or B.

Quantum Physics Mach-Zehnder Interferometer Quantum Particle - Conclusion Y P P X X S 4 P P S 1 A P P B Operator Hadamard matrix S 1 A P B Let the particle be undisturbed between beam splitter S 1 and S 2. Detect the particle after beam splitter S 2. The particle out-path is X if in-path is A. The particle out-path is Y if in-path is B.