Quantum Numbers Mr Tsigaridis Quantum Mechanics We have

Quantum Numbers Mr. Tsigaridis

Quantum Mechanics We have discussed thus far in the course the wave-particle duality in some length The Heisenberg uncertainty principle, as discussed last class briefly, is a fundamental principle of quantum theory Heisenberg’s theory says that you can know a particles position, but you can not know that same particles momentum, or vice versa Since that theory science has been trying to identify how to determine both of these quantities at the same time

Quantum Mechanics Luckily, we have developed mathematics called statistics that can help us in predicting the likelihood of finding an electron at a particular point around the nucleus In particular, an equation called Schrödinger’s wave equation

Schrödinger’s Wave Equation The equation can be used to determine the behaviour of electrons in atoms, specifically, the probability that electrons are at a given point in space and time With modern day computers, we can actually develop ways in which we can map the probability of electrons being found in a specific part of an atom. Theses are called electron probability graphs

Electron Probability Graphs

Quantum Numbers Quantum numbers can be used to describe the position and orientation, spin and energy level of each electron in an atom To do this, values are placed on each electron that describe its location much like a complete address for a house

Principal Quantum Number The principle quantum number describes the ground state of an element It represents the energy level that the electron exists at This number is denoted by the letter n These numbers are whole numbers starting at n=1 and continue until n=∞

Principal Quantum Number The principle quantum number represents the energy level of a certain electron and it also, and more importantly represents the size of the orbital This has an affect on the physical and chemical properties of an atom which we will be discussing further The important thing we have to remember about the first quantum number is that it is represents the energy contribution with the momentum contribution left out

Principal Quantum Number This numbers only depends on the distance that an electron is from the nucleus (radial distance) It is the probability of finding an electron at a specific distance from the nucleus

Azimuthal Quantum Number The second of the quantum numbers, the Azithmal Quantum Number, is also known as the angular momentum quantum number because it includes the momentum of the electron in orbit This quantum number is denoted by the letter l It can have a value of anything up to n-1 If n=1 then l = 0 Similarly if n=3 then l = 0, l = 1 , or l = 2

Azimuthal Quantum Number The second quantum number represents the angular momentum Angular momentum is a vector quantity that represents the electrons position and its momentum Each of the two are controlled by their own operators with x, y, z co-ordinates Heisenberg’s uncertainty principle tells us that not all six of these quantities can be known simultaneously with arbitrary precision

Azimuthal Quantum Number In chemistry this number is vital in its importance since it describes the shape of the orbital that an electron can delve in It strongly influences chemical bonds and bond angles

Azimuthal Quantum Number In some contexts and for the purposes of this course, the l = 0 represents the “s” orbital, l = 1 represents the “p” orbitals, or l = 2 represents the “d” orbitals

Magnetic Quantum Number The third quantum number, The Magnetic Quantum Number, is denoted by ml It is also known as the orbital orientation quantum number as it gives rise to the orientation or direction of each orbital in 3 D space along the three axis It is representative of the orbital angular momentum of an electron along a specified axis

Magnetic Quantum Number Its values can range anywhere between –l to +l If l =0 then ml =0 Similarly if l =1, ml =-1, ml =0, ml =1 When l =0 it corresponds to the s orbital, there is no specific directional values for ml When l =1 it corresponds to the p orbitals, and gives rise to three possibilities for as stated before The additional quantum numbers are required to specify the particular direction along the axis that these orbitals are alligned

Magnetic Quantum Number Notice that as the “p” orbitals are placed together on the same Cartesian plane they form almost a sphere, much like the sphere of the “s” orbitals in which they will fit

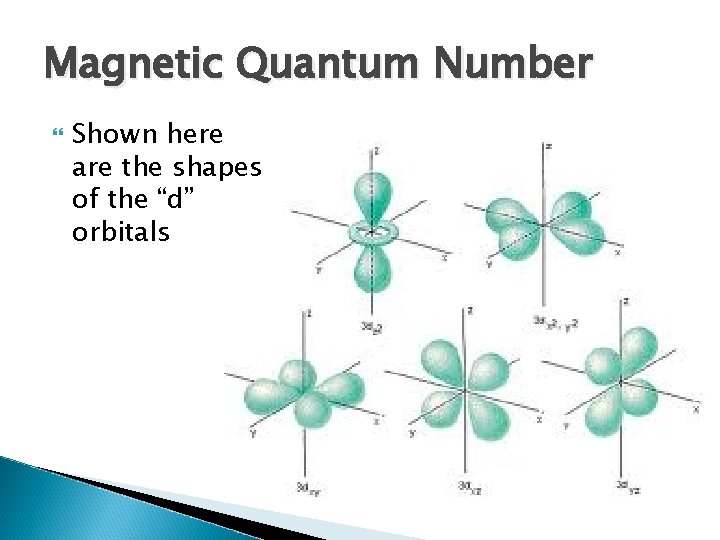
Magnetic Quantum Number Shown here are the shapes of the “d” orbitals

Magnetic Spin Quantum Number The last of the quantum numbers, the magnetic spin quantum number, is denoted by ms The number can have values that are either +½ or -½ They represent the spin orientation of each electron When electrons occupy orbitals they occupy them in pairs and a pair of electrons, in order to occupy the same orbital and part of orbital must have opposite spins

Magnetic Spin Quantum Number Certain fundamental particles have associated with them a magnetic moment that can align itself in either of two directions with respect to an external magnetic field The idea that no two identical electrons can occupy the same point in space is known as the Pauli Exclusion principle By having different spins, the electrons are able to co-exist at the same energy level even though they are different

Quantum Numbers Two electrons in a single orbital are often referred to as an electron pair The electrons and their configurations are described by the four quantum numbers Each number represents an ever increasing accuracy of identifying where in an atom an electron exists As previously stated the electrons quantum numbers are like an address system for each electron, each one being unique

Quantum Numbers The quantum numbers have the following analogy which helps us understand what the quantum numbers represent in terms of the location and orientation of electrons within atoms Principal Quantum Number – What country Azimuthal Quantum Number – What city Magnetic Quantum Number – What street Magnetic Spin Quantum Number – What house