Quantum metrology frontiers with cold atoms ICNFP 2018









- Slides: 34

Quantum metrology frontiers with cold atoms ICNFP 2018 Onur Hosten STANFORD UNIVERSITY || IST AUSTRIA

Quantum and precision sensing with atoms Atomic clocks (resolve gravitational time dilation) Molecules for Electron EDM searches energy level shifts in E field (constraining supersymmetry) Atom interferometers (Testing Einstein’s equivalence principle) (Gravitational wave detection) (Searches of dark energy) (Gravimetry, inertial navigation) In common: • Reduce to sensing w/ two-level quantum system • Can be improved via entanglement (strict sense quantum metrology)

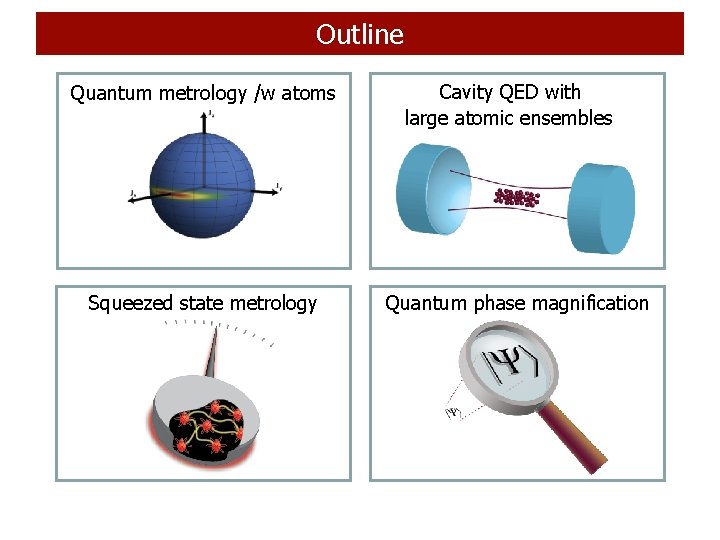
Outline Quantum metrology /w atoms Squeezed state metrology Cavity QED with large atomic ensembles Quantum phase magnification

A formal view for atomic sensors N 2 -level atoms: Spin ½ systems (87 Rb hyperfine clock states) Spin N/2 system: Collective angular momentum vector J Jz Jx Jy

Spin Squeezed Atomic States Spin squeezed states:

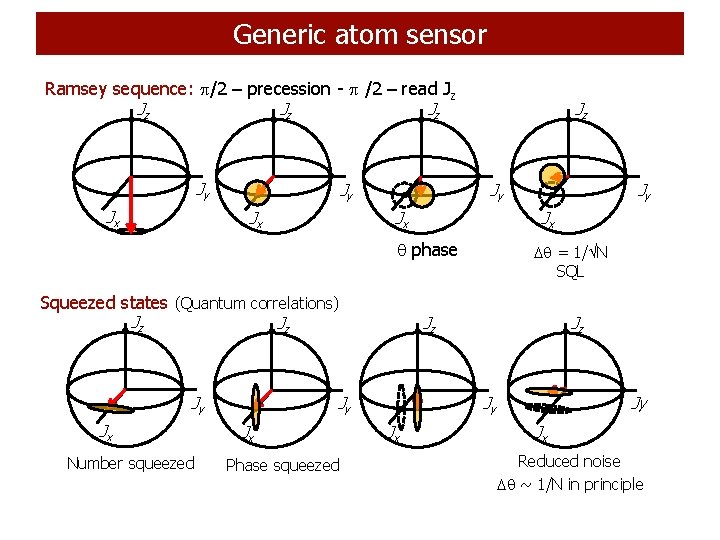
Generic atom sensor Ramsey sequence: /2 – precession - /2 – read Jz Jz Jy Jx Jx phase Squeezed states (Quantum correlations) Jz Jz Jy Jx Number squeezed Phase squeezed = 1/ N SQL Jz Jy Jx Reduced noise ~ 1/N in principle

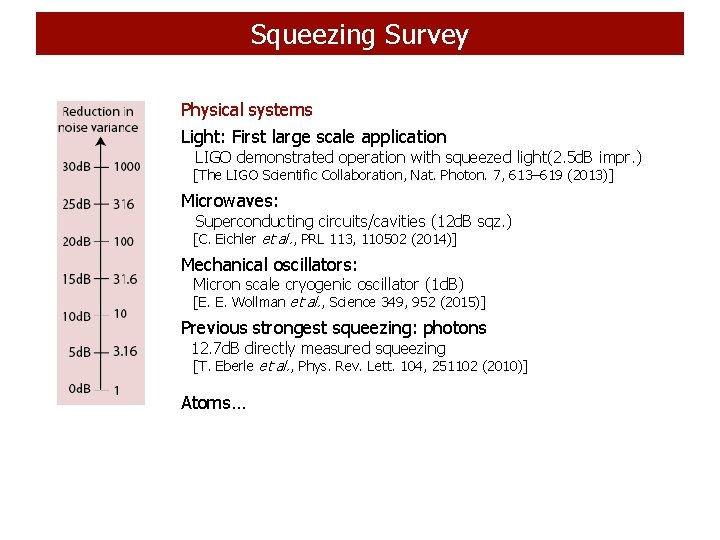
Squeezing Survey Physical systems Light: First large scale application LIGO demonstrated operation with squeezed light(2. 5 d. B impr. ) [The LIGO Scientific Collaboration, Nat. Photon. 7, 613– 619 (2013)] Microwaves: Superconducting circuits/cavities (12 d. B sqz. ) [C. Eichler et al. , PRL 113, 110502 (2014)] Mechanical oscillators: Micron scale cryogenic oscillator (1 d. B) [E. E. Wollman et al. , Science 349, 952 (2015)] Previous strongest squeezing: photons 12. 7 d. B directly measured squeezing [T. Eberle et al. , Phys. Rev. Lett. 104, 251102 (2010)] Atoms…

Outline Quantum metrology /w atoms Squeezed state metrology Cavity QED with large atomic ensembles Quantum phase magnification

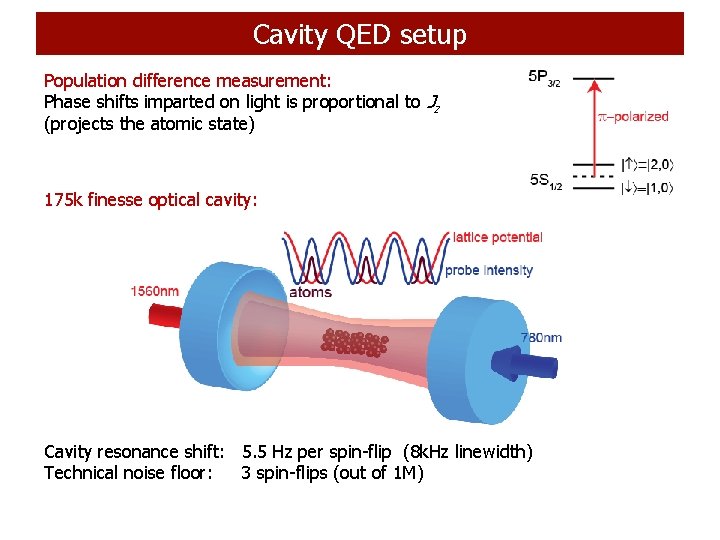
Cavity QED setup Population difference measurement: Phase shifts imparted on light is proportional to Jz (projects the atomic state) 175 k finesse optical cavity: Cavity resonance shift: 5. 5 Hz per spin-flip (8 k. Hz linewidth) Technical noise floor: 3 spin-flips (out of 1 M)

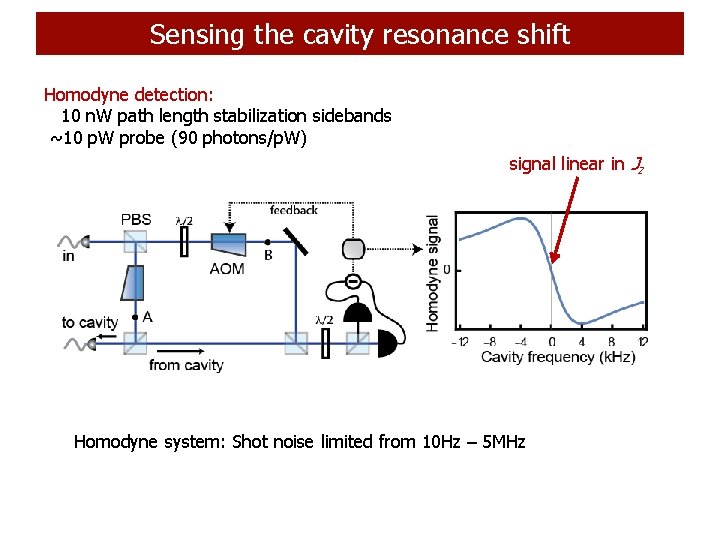
Sensing the cavity resonance shift Homodyne detection: 10 n. W path length stabilization sidebands ~10 p. W probe (90 photons/p. W) signal linear in Jz Homodyne system: Shot noise limited from 10 Hz – 5 MHz

The Apparatus

Outline Quantum metrology /w atoms Squeezed state metrology Cavity QED with large atomic ensembles Quantum phase magnification

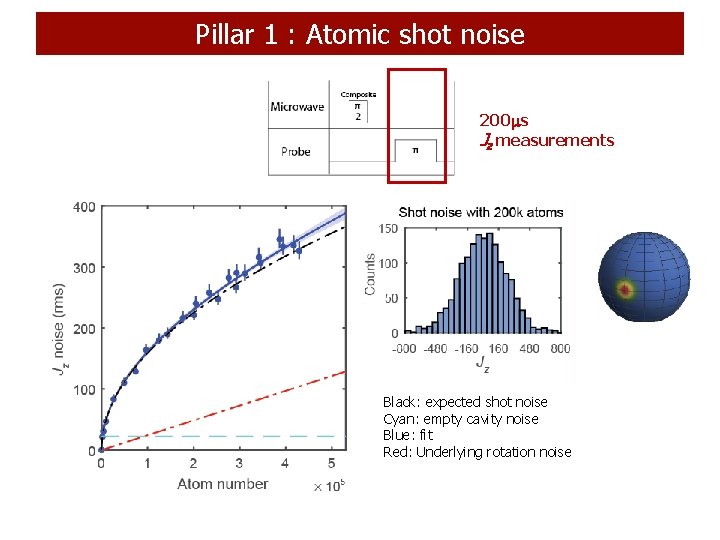
Pillar 1 : Atomic shot noise 200 s Jz measurements Black: expected shot noise Cyan: empty cavity noise Blue: fit Red: Underlying rotation noise

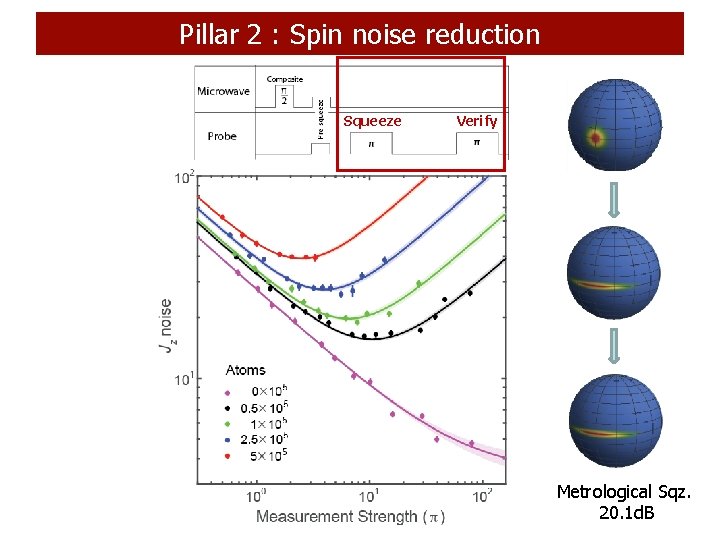
Pillar 2 : Spin noise reduction Squeeze Verify Metrological Sqz. 20. 1 d. B

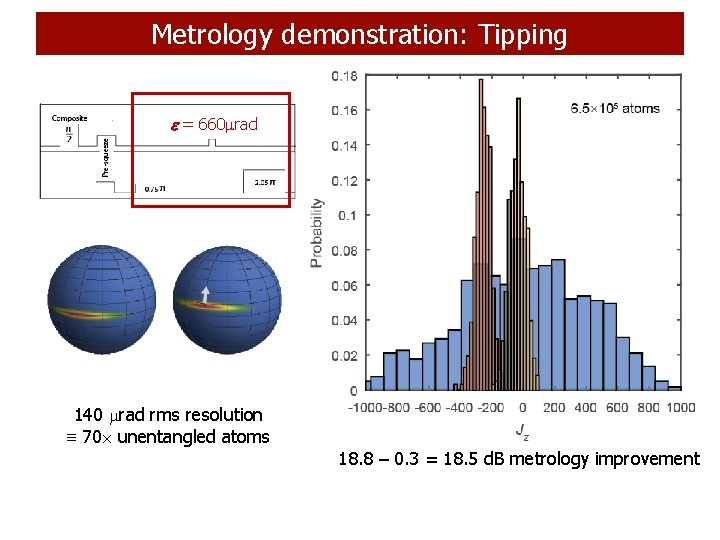
Metrology demonstration: Tipping = 660 rad 140 rad rms resolution 70 unentangled atoms 18. 8 – 0. 3 = 18. 5 d. B metrology improvement

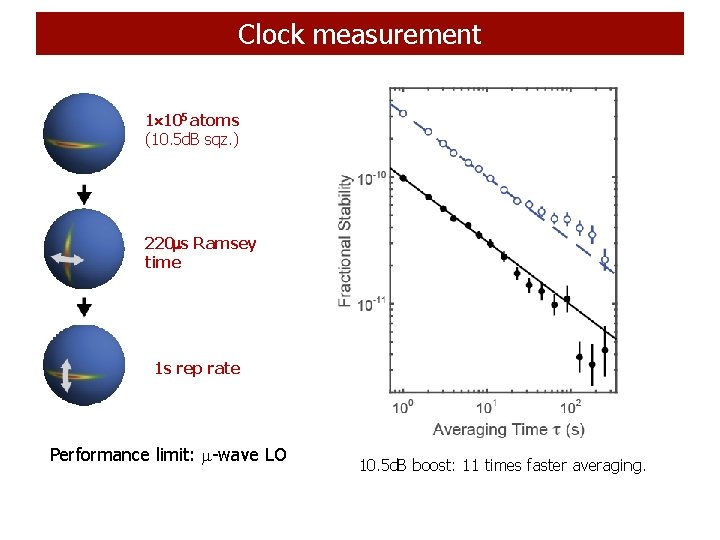
Clock measurement 1 105 atoms (10. 5 d. B sqz. ) 220 s Ramsey time 1 s rep rate Performance limit: -wave LO 10. 5 d. B boost: 11 times faster averaging.

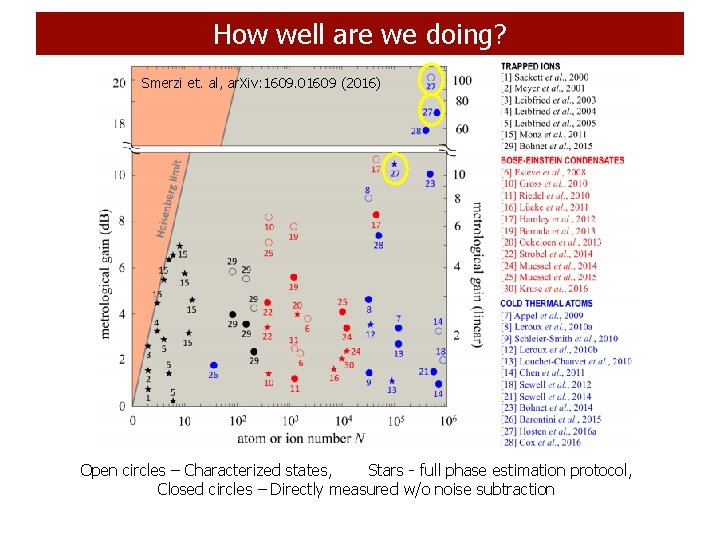
How well are we doing? Smerzi et. al, ar. Xiv: 1609. 01609 (2016) Open circles – Characterized states, Stars - full phase estimation protocol, Closed circles – Directly measured w/o noise subtraction

Outline Quantum metrology /w atoms Squeezed state metrology Cavity QED with large atomic ensembles Quantum phase magnification

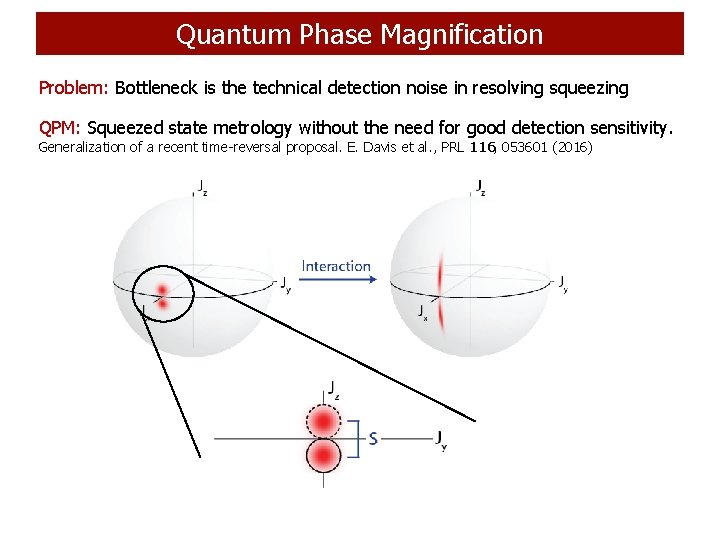
Quantum Phase Magnification Problem: Bottleneck is the technical detection noise in resolving squeezing QPM: Squeezed state metrology without the need for good detection sensitivity. Generalization of a recent time-reversal proposal. E. Davis et al. , PRL 116, 053601 (2016)

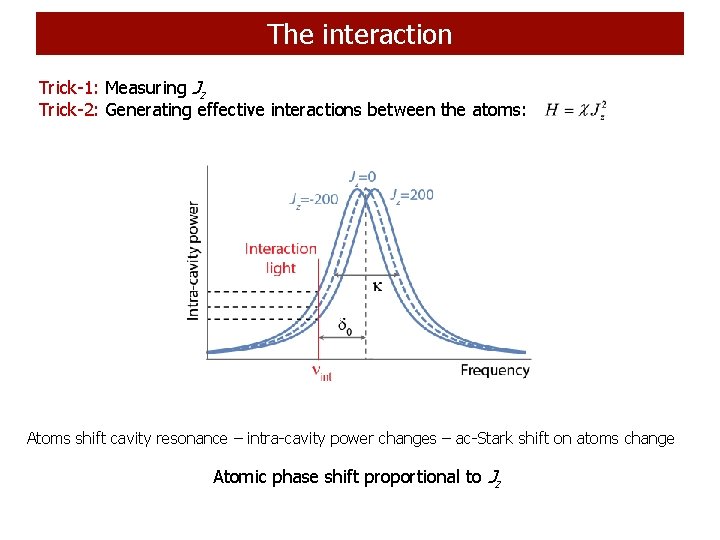
The interaction Trick-1: Measuring Jz Trick-2: Generating effective interactions between the atoms: Atoms shift cavity resonance – intra-cavity power changes – ac-Stark shift on atoms change Atomic phase shift proportional to Jz

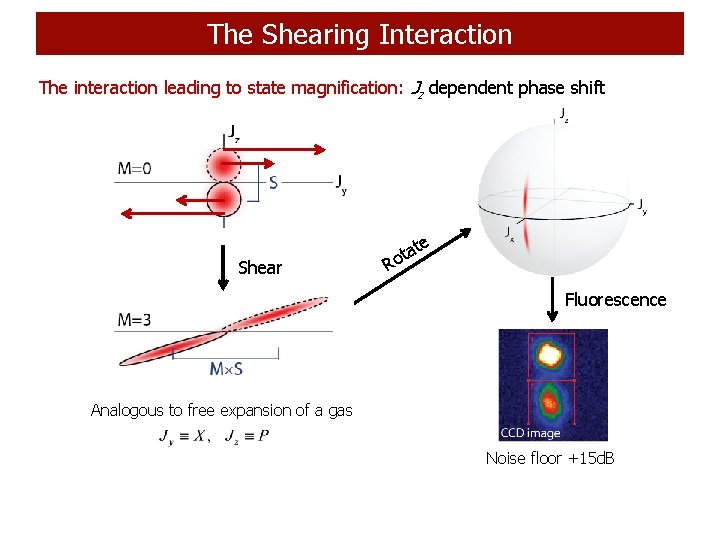
The Shearing Interaction The interaction leading to state magnification: Jz dependent phase shift Shear t ota e R Fluorescence Analogous to free expansion of a gas Noise floor +15 d. B

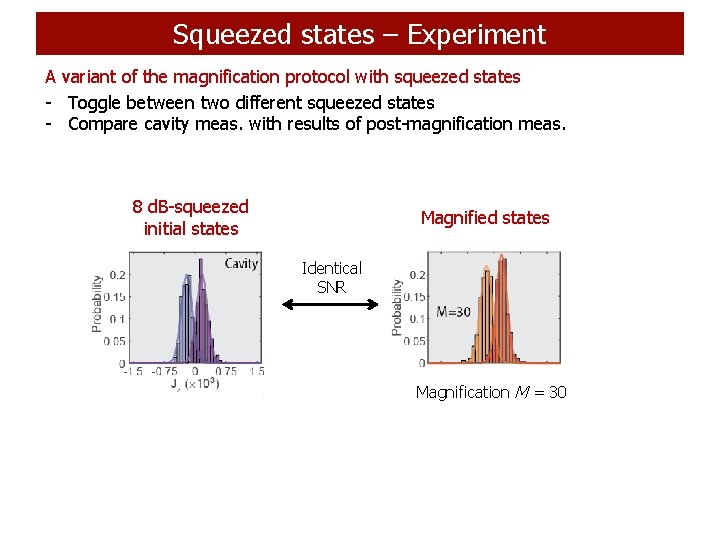
Squeezed states – Experiment A variant of the magnification protocol with squeezed states - Toggle between two different squeezed states - Compare cavity meas. with results of post-magnification meas. 8 d. B-squeezed initial states Magnified states Identical SNR Magnification M = 30

Final remarks Entanglement & Bell Correlations: - Atoms entangled in groups of > n=1590. - 124 -sigma Bell correlation witness w/ 5 x 105 atoms. - Fountain clock w/ fluorescence measurements 6 d. B squeezing Outlook: Map spin into spatial superpositions generate non-classical collective motional states

Acknowledgements PI Mark Kasevich Res. Sci. Onur Hosten Graduate students Rajiv Krishnakumar Nils Engelsen Postdoc Julian Martinez Yunfan Wu Funding: DTRA, ONR Benjamin Pitchler

Refs. References Squeezing: O. Hosten, N. J. Engelsen, R. Krishnakumar, M. Kasevich, Nature 529, 505 (2016) Phase magnification: O. Hosten, R. Krishnakumar, N. J. Engelsen, M. Kasevich, Science 352, 1552 (2016) Bell Correlations: N. J. Engelsen, R. Krishnakumar, O. Hosten , M. Kasevich, PRL, March 24 (2017)

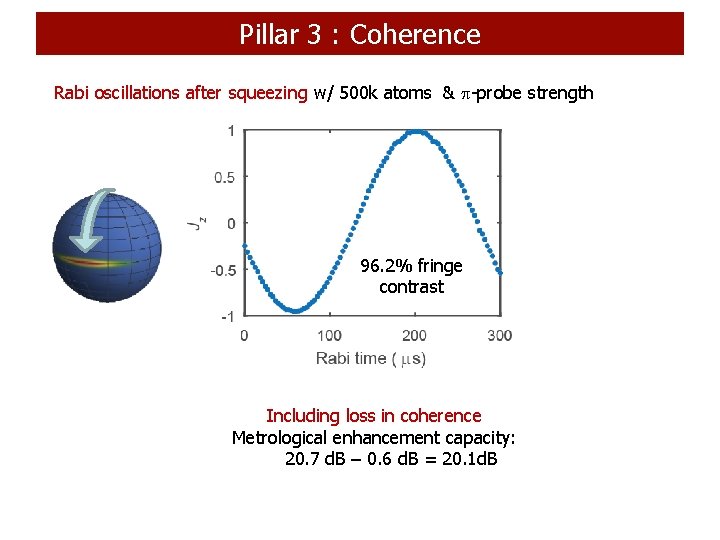
Pillar 3 : Coherence Rabi oscillations after squeezing w/ 500 k atoms & -probe strength 96. 2% fringe contrast Including loss in coherence Metrological enhancement capacity: 20. 7 d. B – 0. 6 d. B = 20. 1 d. B

Backup slides

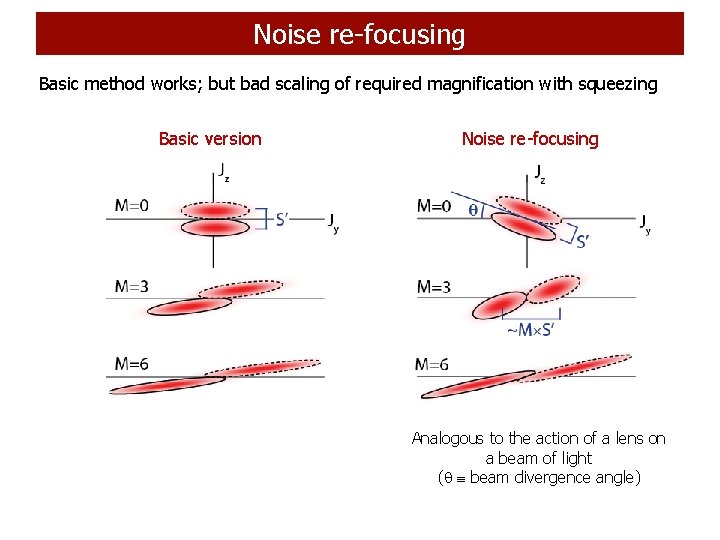
Noise re-focusing Basic method works; but bad scaling of required magnification with squeezing Basic version Noise re-focusing Analogous to the action of a lens on a beam of light ( beam divergence angle)

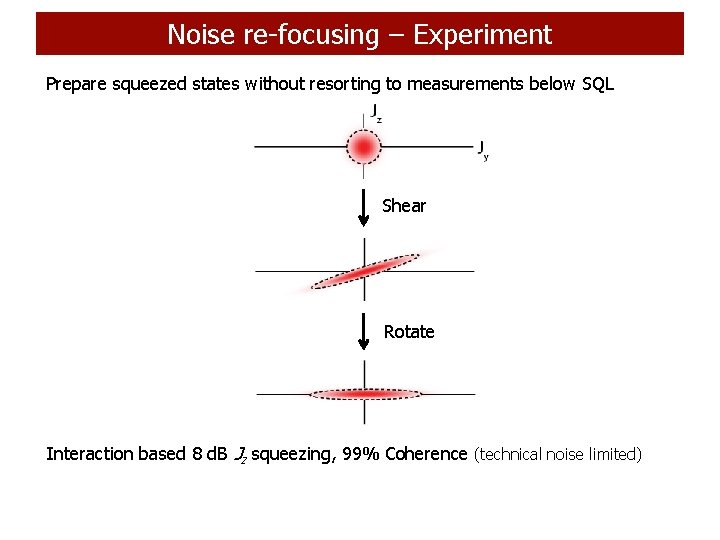
Noise re-focusing – Experiment Prepare squeezed states without resorting to measurements below SQL Shear Rotate Interaction based 8 d. B Jz squeezing, 99% Coherence (technical noise limited)

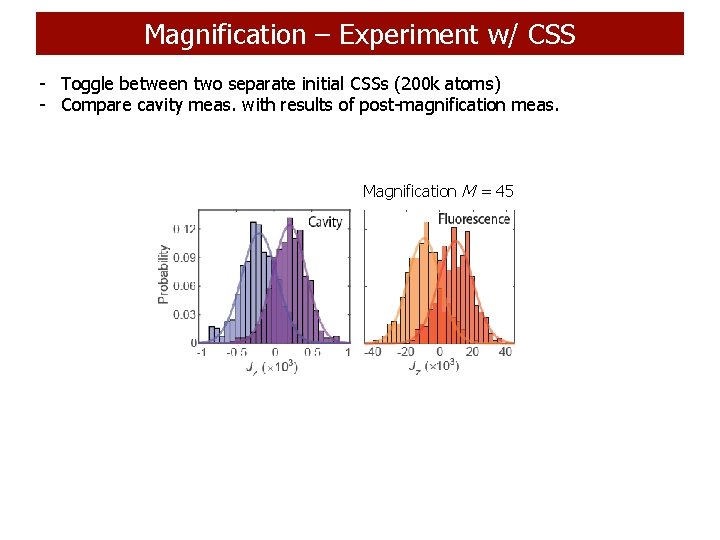
Magnification – Experiment w/ CSS - Toggle between two separate initial CSSs (200 k atoms) - Compare cavity meas. with results of post-magnification meas. Magnification M = 45

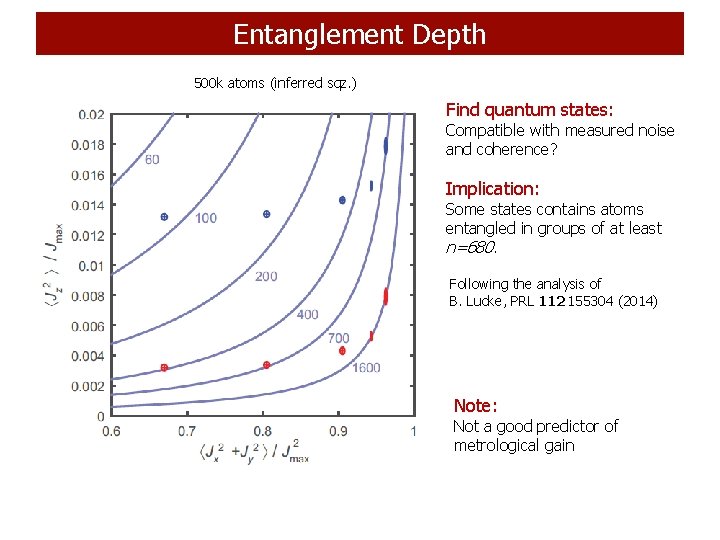
Entanglement Depth 500 k atoms (inferred sqz. ) Find quantum states: Compatible with measured noise and coherence? Implication: Some states contains atoms entangled in groups of at least n=680. Following the analysis of B. Lucke, PRL 112 155304 (2014) Note: Not a good predictor of metrological gain

How well can you resolve Jz Optimal probing of the 87 Rb clock transition Saturation due to finite hyperfine splitting Absorption reduces measurement sensitivity Jz variance: Competing noise sources Photon shot noise Max. -28 d. B (-24 d. B) Spontaneous Raman scattering (spin-flips) : Detection efficiency ~ 0. 16 C: Cooperativity ~1

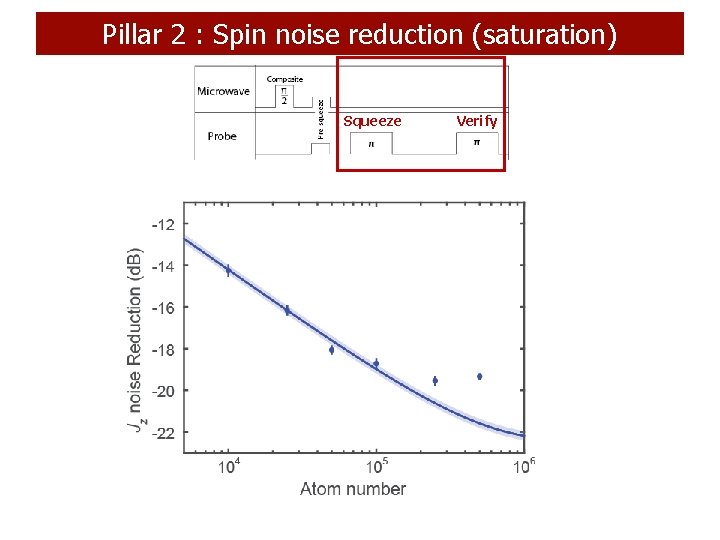
Pillar 2 : Spin noise reduction (saturation) Squeeze Verify

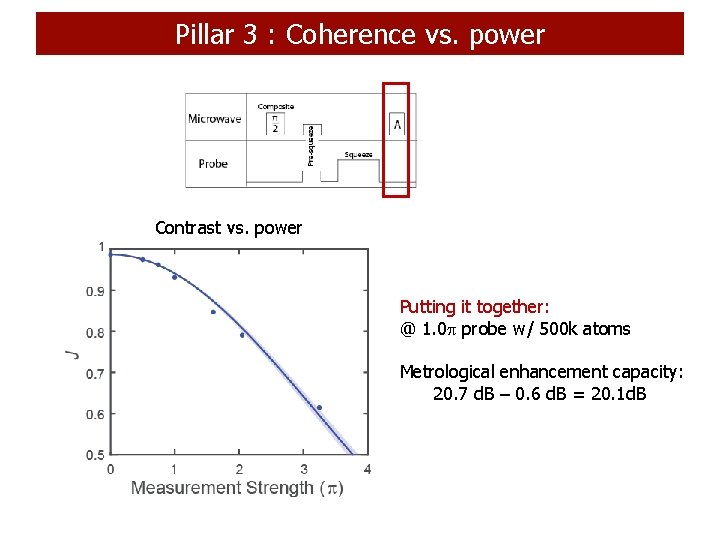
Pillar 3 : Coherence vs. power Contrast vs. power Putting it together: @ 1. 0 probe w/ 500 k atoms Metrological enhancement capacity: 20. 7 d. B – 0. 6 d. B = 20. 1 d. B