Quantum Mechanics Atomic Structure l Electron Cloud Model

Quantum Mechanics

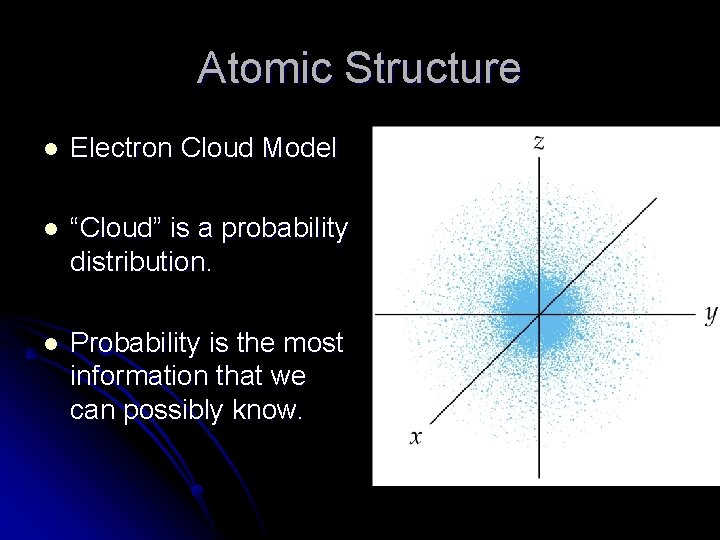
Atomic Structure l Electron Cloud Model l “Cloud” is a probability distribution. l Probability is the most information that we can possibly know.

Schrödinger Wave Equation l Allows you to calculate the probability of an electron being in a given place and energy. l Gives us a good idea of where the electrons are in an atom.

Quantum Numbers l Address of an electron in an atom l The collection of 4 quantum numbers gives you as much information as you can possibly get for a particular electron. l Describes a hierarchical structure l l Shell Subshell Orbitals Electron Spin States

Principle Quantum Number How far from the nucleus an electron is. l Also describes most of the energy. l Will be integers from 1 to 7 for our purposes. l Call this the “shell” the electron is in. l l n = 1 (the first shell) is shell closest to nucleus with lowest energy n

Angular Momentum Quantum Number l l Angular momentum describes movement in circles. Describes the shape of the area an electron is in. Can be integers from 0 through 3 Usually called the “sub-shell” ℓ A cursive L

Angular Momentum Quantum Number l Specific Values have specific names ℓ = 0 is called an s subshell l ℓ = 1 is called a p subshell l ℓ = 2 is called a d subshell l ℓ = 3 is called a f subshell l

s Orbitals within an s Subshell l Have a spherical shape

p Orbitals within a p Subshell l Have a dumbbell shape

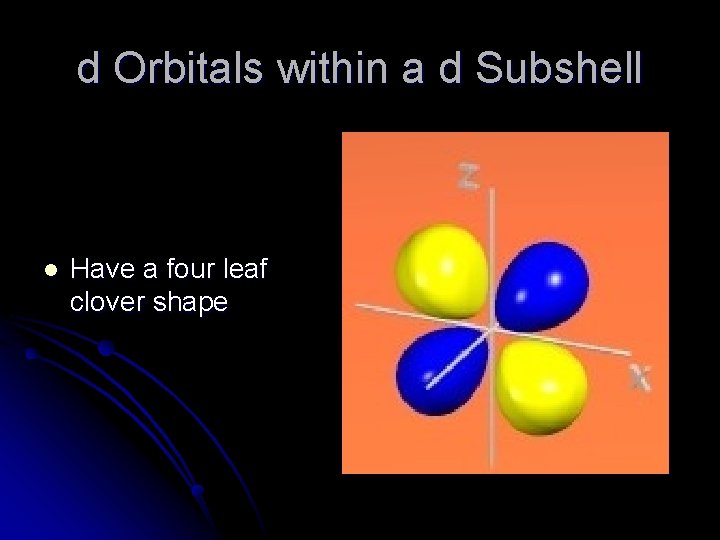
d Orbitals within a d Subshell l Have a four leaf clover shape

f Orbitals within an f Subshell l Look like two d orbitals pushed together in the middle

Magnetic Quantum Number l Describe which direction the shapes point in space. l Refers to specific orbitals l Orbital – area of space analogous to an orbit but taking probability into account l Each orbital holds up to two electrons. mℓ m with a subscript L

Magnetic Quantum Number l l Only one direction in space for a sphere Only one s orbital

Magnetic Quantum Number l There are three directions for p orbitals to point l There are three p orbitals

Magnetic Quantum Number l There are five solutions for the d orbitals

Magnetic Quantum Number l Seven f orbitals

Magnetic Quantum Number l n = 1 is where the s subshells start l n = 2 is where the p subshells start l n = 3 is where the d subshells start l n = 4 is where the f subshells start

Spin Quantum Number l Describes the spin of an electron l Imagine a top spinning on its axis l Can either be +½ or -½ ms m with a subscript s

For the Math People l For a given electron l n = [1, 2, 3, 4, 5, 6, or 7] l ℓ = [0, … n – 1] l mℓ = [-ℓ … +ℓ] l ms = [-½, +½]

How do we apply all this to electrons? l Aufbau Principle – fill up electrons in the lowest energy first l Use the diagonal line diagram.

Hydrogen l Start with the simplest atom. l Has one electron

Orbital Filling Diagrams l Use horizontal lines to represent an orbital Use half arrows to represent electrons l Arrow up means spin +½ l Arrow down means spin -½ l

Helium l Has two electrons l Where do you put the extra electron? l Pauli Exclusion Principle – No two electrons in the same atom can have the same set of four quantum numbers l Practically this means two electrons in the same orbital must have opposite spins.

More Elements l Lithium l Three l electrons Beryllium l Four electrons

Boron 5 electrons l Does it matter which p-orbital you put the electron in? l No because they are all equivalent l l Degenerate – have the same energy

Carbon l Six electrons l Where does the sixth electron go? l Hund’s Rule – Electrons stay unpaired as long as possible.

More Elements l Nitrogen l 7 l Oxygen l 8 l electrons Fluorine l 9 l electrons Neon l 10 electrons

More Elements l Chromium l Krypton

More Elements l Tin l Promethium

Even More Elements l Tungsten l Lead

Even More Elements l Plutonium l Bohrium